基于考虑气温影响的门限自回归移动平均模型居民日用电负荷预测

孙玉芹，王亚文，朱威，李彦

(上海电力大学数理学院，上海市 200090)

0 引 言

电力负荷预测是电力公司进行能源管理的关键。作为电力领域研究的重要问题，电力负荷预测既能为电力系统的安全运行提供保障，又可以为制定供电计划提供有效的理论支持[1]。所以，具有较高预测精度的负荷预测方法，是理论研究的重点。由于电力负荷往往会受到多种因素的影响，电力负荷常表现为非线性、非平稳和周期性[2-3]，导致其精确预测的难度也随之提高。

目前，常用的短期电力负荷预测的方法主要有：统计学方法[4-10]、传统机器学习方法[11-16]和深度学习方法[17-20]。其中，统计学方法分为两类，一类是时间序列建模方法。文献[4]针对电力负荷序列的波动性，使用区间时间序列向量自回归模型提高了负荷预测精度。文献[5]结合Java的多线程技术，基于自回归差分移动平均(autoregressive integrated moving average，ARIMA)模型实现了R语言在电力负荷预测中的高效并行运算。文献[6]考虑温度对夏季电力负荷的影响，利用带有协变量的ARIMA模型提高了负荷的预测精度。文献[7]首次采用自激门限自回归(self-excitation threshold autoregressive，SETAR)模型对日负荷进行预测，解释了负荷序列的非线性特征。虽然上述方法相对简单易行、计算速度较快，但是只将气温和负荷非线性特性两个因素中的一种作为研究内容。另一类是以时间序列模型为基础的组合模型方法。文献[8]构建了季节自回归差分移动平均、广义回归神经网络和支持向量机三者结合的组合模型；文献[9]提出了ARIMA和在线循环神经网络的组合模型；文献[10]采用集合经验模式分解的方法，并结合长短期记忆网络和ARIMA模型对负荷进行短期预测。这些文献使用的方法与单一模型相比，在负荷预测精度上提高不少，但模型机理和内置参数复杂，对硬件配置要求较高，需要大量的数据训练模型才能发挥机器学习的优势，在小容量数据下的预测效果较差；当处理不同的数据时，通常需要反复地调整超参数，建模所需时间成本较高[21]。

本文在考虑气温对负荷影响的同时，兼顾负荷的非线性特征，利用气温与居民用电负荷的关系，以气温突变点为门限，将居民用电负荷时间序列分为两段，每段为一个机制。根据负荷时间序列的非线性特征，建立以气温为协变量的门限自回归移动平均(threshold autoregressive moving average with exogenous variable，TARMAX)模型。利用气象预报30天的气温预报功能，对不同气温影响下的浙江省西南某地级市居民日用电负荷进行预测。实例结果表明：该方法在居民用电负荷预测方面表现更优。

1 居民用电负荷的非线性特征

1.1 气温与居民用电负荷的相关性分析

许多研究表明：影响居民用电负荷的主要因素有各种气象因素、节假日、重大事件等，其中气温的影响最大[22-23]。随着生活水平的提高，用户对生活舒适度的追求也相应提高，在温度较高或较低时，都采用风扇、空调或取暖设备等保持适宜的温度环境。特别是在极端气温情况下，长时间且大量地使用设备更容易增大负荷的峰谷差，影响全网的供电质量。而且居民用电负荷和气温的时间序列都具有非线性特征，如图1所示，给负荷分析和预测造成不便。

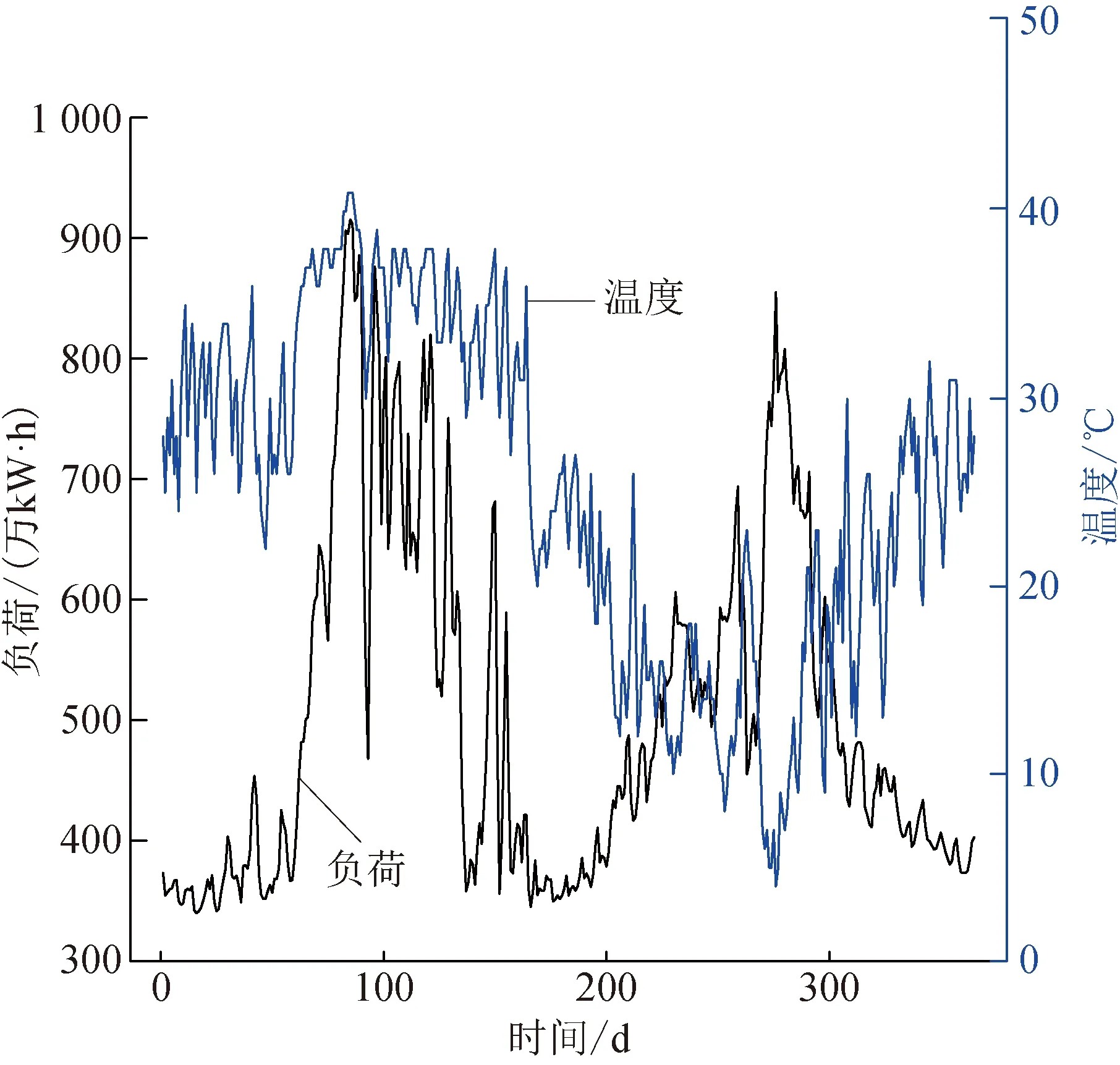
图1 某居民用电负荷与最高气温的时间序列图

通常采集到的气温数据有最高气温、最低气温和平均气温，三者与负荷的相关度大小由相关系数判断。

Pearson相关系数计算如式(1)所示：

(1)

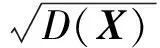
以浙江省西南某地级市2017年8月份气温与负荷数据为例，表1给出了气温与居民用电负荷的Pearson相关系数。通过分析表明：最高气温对居民用电负荷的影响最大，故将最高气温作为负荷协变量的最佳选择。

表1 气温与居民用电负荷的相关度

1.2 居民用电负荷的门限效应

图2为浙江省西南某地级市2017年居民用电负荷和日最高气温的散点图。最高气温存在“拐点”，又称为突变点，将负荷序列分为两个集群。若以该突变点为门限，门限左侧的负荷序列与最高气温表现为负相关，右侧表现为正相关。

图2 居民日用电负荷-日最高气温散点图

如图3所示，大于30 ℃侧和小于30 ℃侧的负荷数据点均不连续，所以不能分别对两个负荷群建立时间序列模型。针对此类负荷时间序列，本文建立以气温为协变量、气温突变点为门限的双体制TARMAX模型。基于TARMAX模型，从整体负荷序列出发，通过比较日最高气温与气温突变点的大小，居民负荷时间序列被分配到2个机制中。

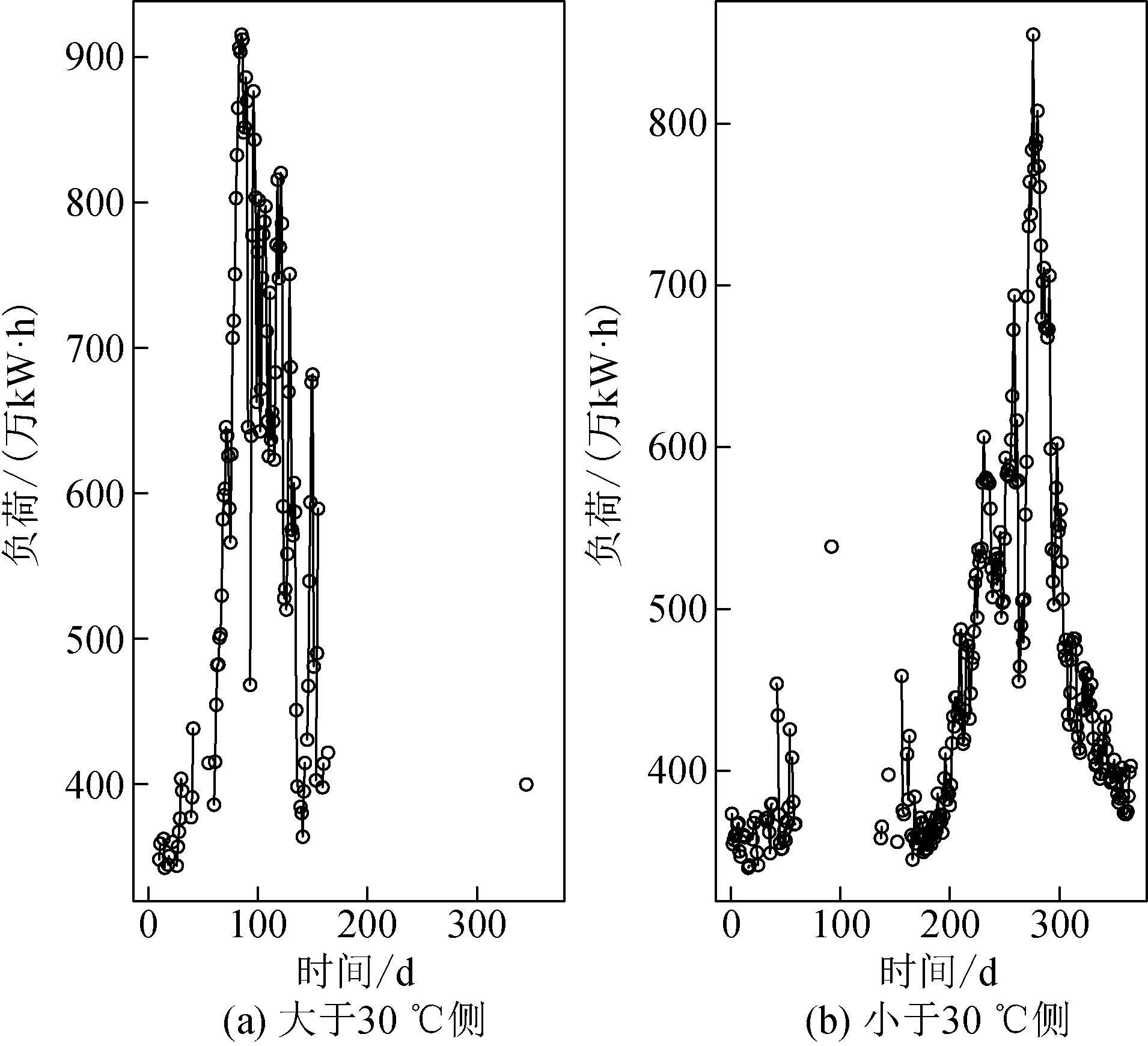
图3 两侧负荷序列图

2 TARMAX负荷预测模型

给定电力负荷时间序列，TARMAX模型[24]结构如下：

(2)

基于TARMAX模型的负荷预测流程如图4所示，随机搜索变量算法得到的最优模型结构中只包含影响显著的滞后项。

图4 负荷预测流程图

2.1 气温突变点搜寻

利用以贝叶斯定理为核心的马尔科夫链蒙特卡洛(Markov chain Monte Carlo，MCMC)算法搜寻气温突变点，需要求得气温突变点的条件后验分布。

2.1.1 气温突变点的条件后验分布

模型式(2)似然函数的矩阵形式近似如下所示：

(3)

式中：n1、n2分别是两个机制中负荷序列的数量；Θk是系数的列向量；Yk是第k个机制中负荷的列向量；Xk是由往期负荷时间序列构成的矩阵。

根据模型参数的先验信息[24]，参数的条件后验分布如式(4)—(7)所示。

参数1：服从多元正态分布：

(4)

参数2：服从逆伽马分布：

(5)

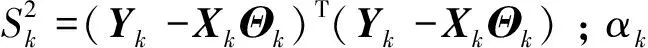
参数3：气温突变点的条件后验分布是非标准分布，近似形式如下：

(6)

参数4：d的条件后验概率函数如下：

(7)

式中：d0是d的超参数。

2.1.2 气温突变点采样

基于条件后验分布的MCMC采样步骤如下：

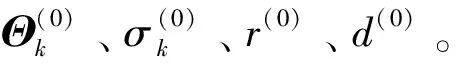
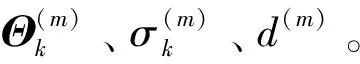
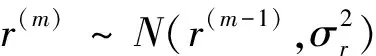
f=min{1,p(r*)/p[r(m-1)]}

(8)

步骤4：记录每次的迭代值，再重复步骤2—3。

2.2 负荷预测模型的确立

负荷模型的结构取决于时间序列模型的滞后项。本文应用随机搜索变量方法[25]选择影响显著的模型系数，以确定模型结构，避免了从庞大的模型群(数量级为107)中筛选最佳模型的困扰。

对于每个可能影响显著的系数，存在与否分别以取值1或0的潜变量s表示，其概率满足：P(s=1)=P(s=0)=0.5。此时，模型系数(以自回归系数为例)的先验分布如下：

φ|s～(1-s)N(0,τ2)+sN(0,c2τ2)

(9)

式中：τ和c是超参数。

潜变量的条件后验分布具有伯努利分布形式，s=1的条件概率为：

(10)

式中：联合概率A=p(φ|s=1)P；Ψ是未知参数的集合；下标-s代表不包括s；联合概率B=p(φ|s=0)(1-P)；P=0.5；p是模型系数在s取不同值时的条件概率。

2.3 预测评价标准

本文选取平均绝对百分比误差(mean absolute percentage error, MAPE)、均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error,MAE)、平均百分比误差(mean percentage error，MPE)和平均误差(mean error, ME)判断模型的预测效果，部分误差的计算式分别为：

(11)

(12)

(13)

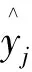
3 算例分析

3.1 数据来源及预处理

实验选取浙江省西南某地级市2017年5月1日到2020年3月31日的居民日平均用电负荷数据。数据取自然对数，使用递归时间窗口预测。为了验证模型在不同气温下的有效性，将2017年5月1日到预测月份前一日的数据作为训练集，分别对2019年6月、9月、12月以及2020年3月等4个不同季节的居民用电负荷进行预测。

3.2 超参数的设置

Vk取值为对角矩阵diag(0.1,0.1,0.1)；门限的超参数可以根据负荷-温度散点图确定，图2中气温的突变点在30 ℃左右，故先验分布U(a,b)中的a与b分别取气温的20%和80%分位数；αk=1，βk=0.5；d0取为4；用于模型选择的超参数的取值应满足：(τ,c)=(σ/4,20)，其中，σ是系数φ的标准差；将不同阶数的模型残差带入赤池信息准则(akaike information criterion, AIC)中，当 AIC最小时，模型最大的滞后阶数取5。整个MCMC过程执行5 000次，将前1 000次作为燃烧期，为了降低初始值的影响，获得近似独立的样本，本文在剩余样本中每隔10个抽取一个用于统计计算，将样本的均值作为参数的估计值。

3.3 模型确立结果

如图5所示，气温突变点(取对数)的采样值集中在3.45附近，累计均值表明样本最终收敛。该采样值对应的实际气温为31.5 ℃，与预期的气温突变点相近。

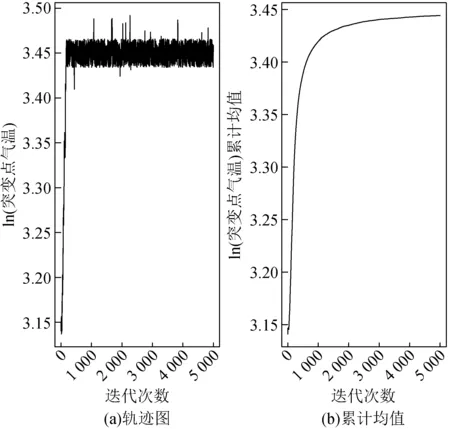
图5 气温突变点的采样结果

在上述气温突变点的基础上，对模型系数进行选择。如图6所示，以每个系数的潜变量的后验概率大于0.5作为系数选择的标准[25]，模型的形式最终确定为：

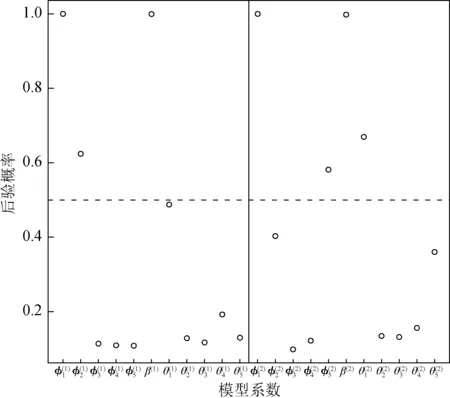
图6 负荷预测模型的选择结果

(14)

3.4 预测结果分析与对比

图7为不同模型对2019年6月居民用电负荷的预测负荷曲线。从图7中可以看出，TARMAX模型的预测值(红色折线)接近负荷的真实值(黑色折线)，预测效果较好；同时，TARMAX模型在峰谷处的预测具有一定优势。而带协变量的自回归移动平均(autoregressive moving average with exogenous variable, ARIMAX)和ARIMA模型的负荷曲线表现为：以真实负荷曲线为中心上下变化，且变化幅度较大。

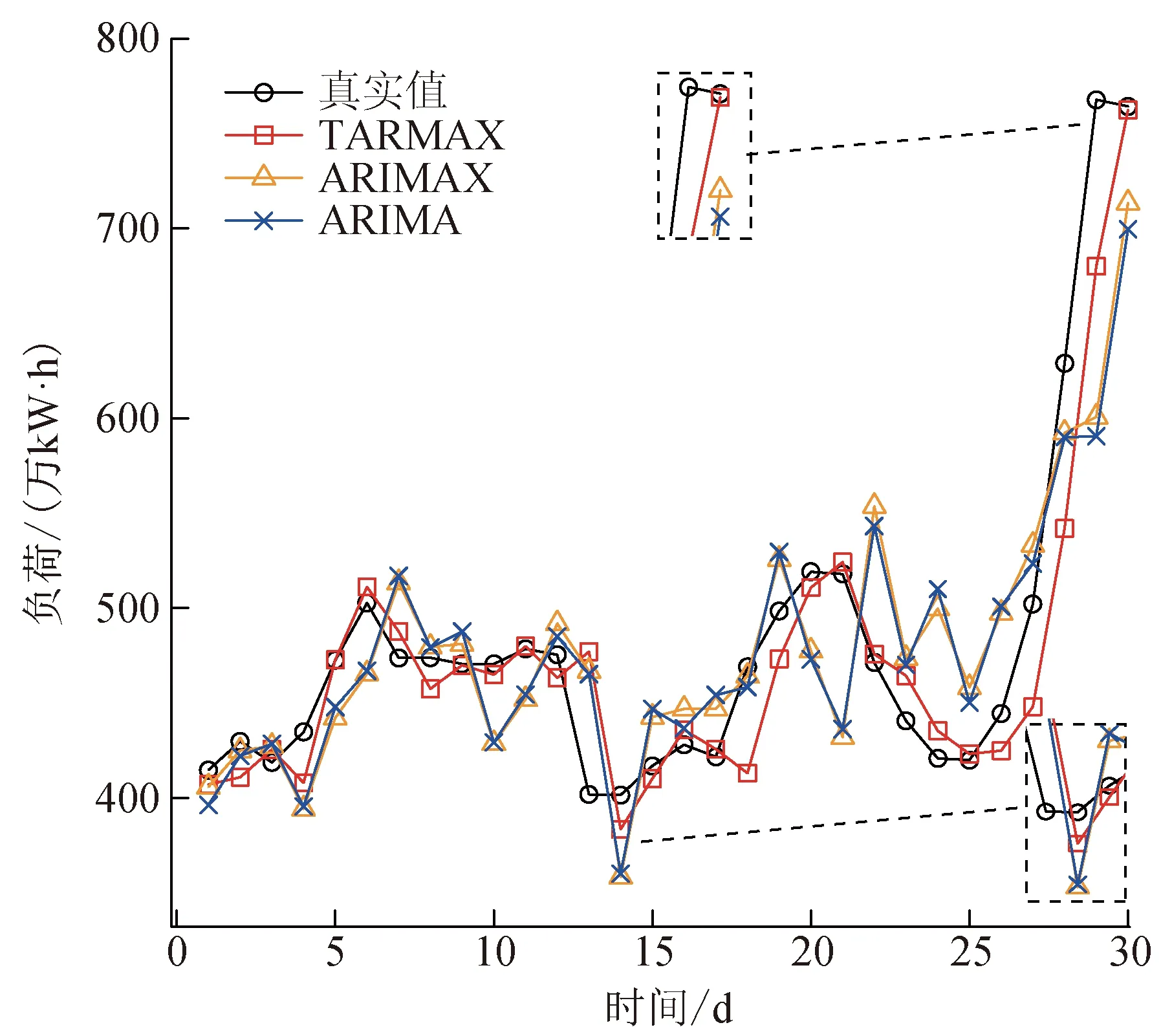
图7 2019年6月居民用电负荷预测结果

表2给出了不同模型的预测误差结果。其中，TARMAX模型的MAPE值为4.167%，与ARIMAX模型相比提高了3.762%；RMSE值为6.833%，相比ARIMAX模型降低了3.753%。表明TARMAX模型的预测精度高于线性时间序列模型。同时，TARMAX模型在小数据量下的预测效果明显优于LSTM和MLP。

表2 2019.6居民用电负荷预测精度

3.5 不同季节负荷预测效果对比

为了进一步验证所提方法的有效性，本文对浙江省西南某地级市2019年9月和12月、2020年3月的居民用电负荷进行预测。不同模型的预测结果如图8至10所示，相比其他模型，TARMAX模型的预测精度更高，且在不同季节的预测表现都较平稳。

图8 2019年9月居民用电负荷预测结果

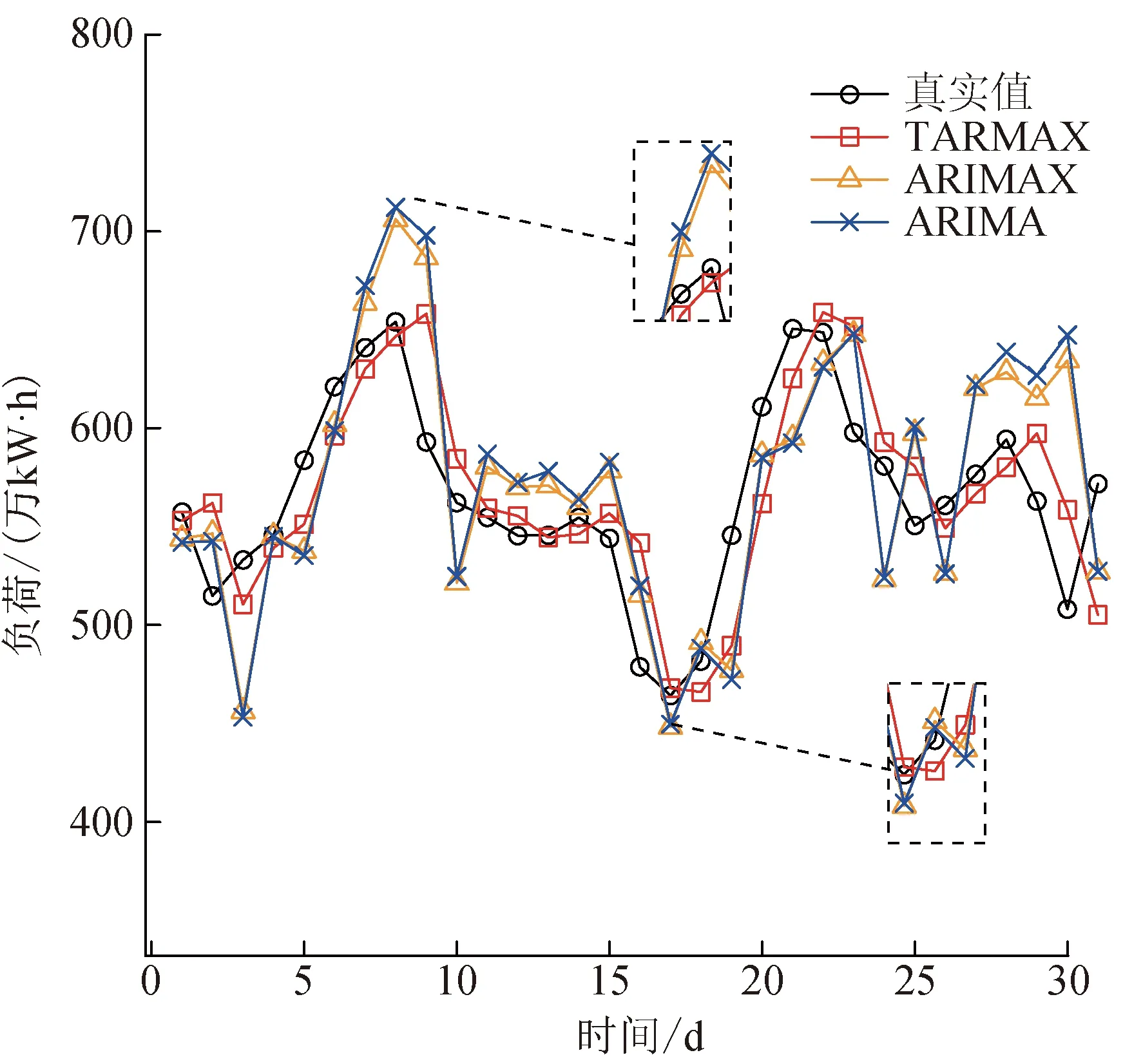
图9 2019年12月居民用电负荷预测结果

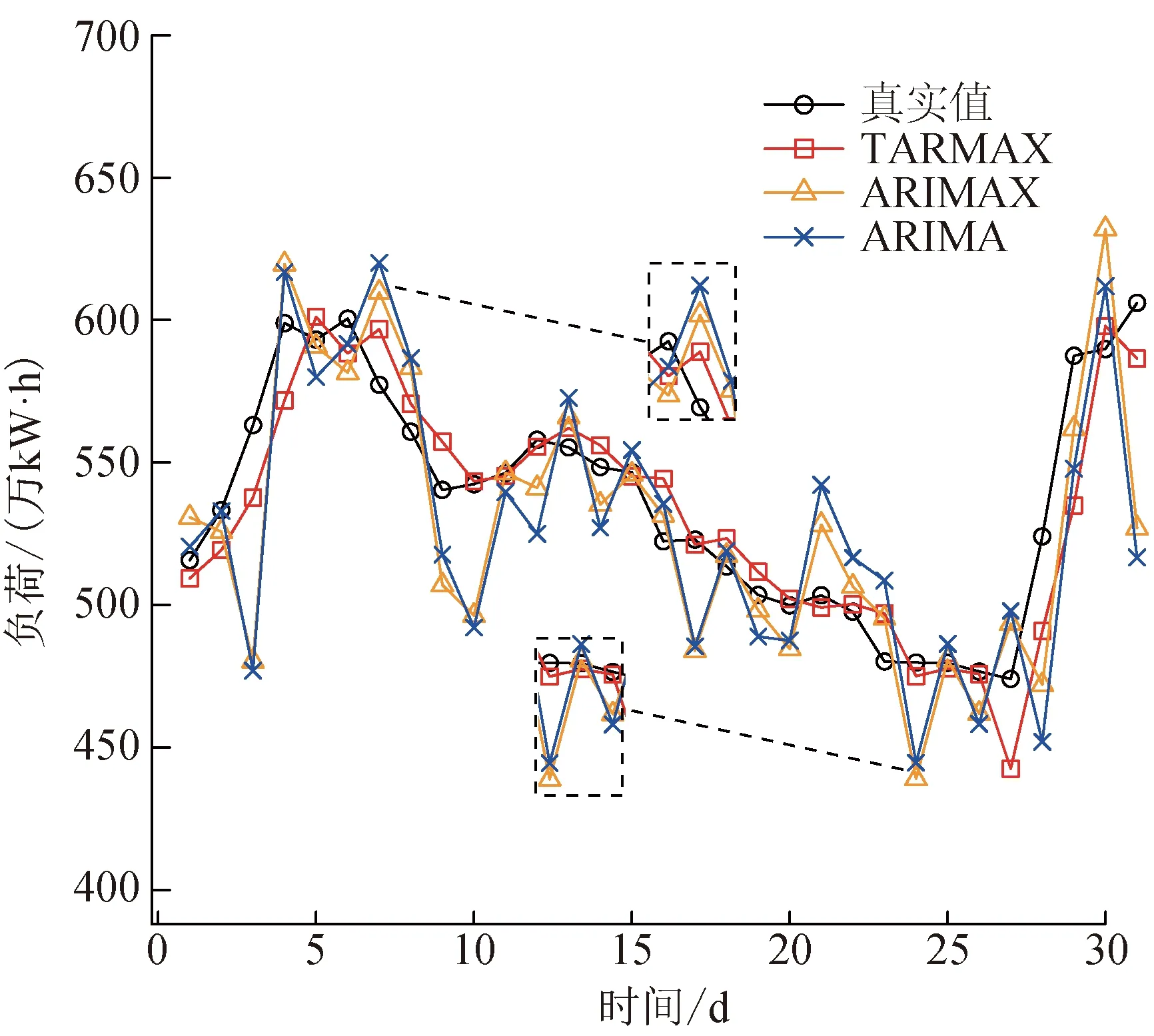
图10 2020年3月居民用电负荷预测结果

表3给出了不同月份的预测误差指标的对比结果。从表3可以看出：TARMAX模型的误差均低于其他模型，MAPE的值基本为ARIMAX模型的一半，相比之下RMSE和其他误差指标也较低；虽然ARIMAX模型的预测误差略低于ARIMA模型，但该模型未考虑非线性因素，所以预测效果略差。总体来说，TARMAX模型在居民用电负荷预测方面效果更优，该模型对不同季节气温影响下的居民用电负荷均有良好的适应能力。

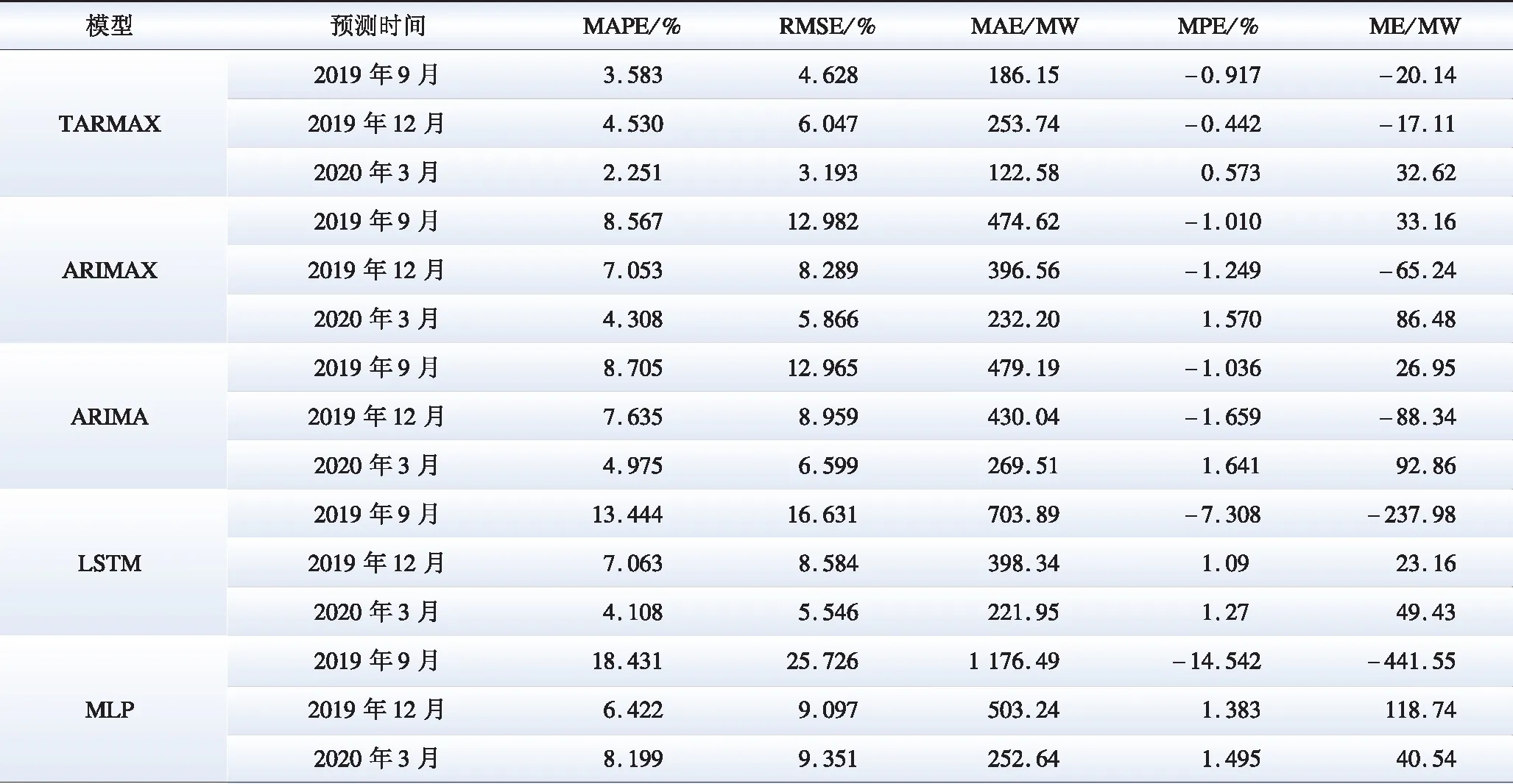
表3 不同月份居民用电负荷预测精度

根据文中1.1节所述，平均气温与负荷的相关系数略小于最高气温的相关系数，为了验证平均气温对居民用电负荷的影响大小，表4给出了以平均气温为协变量的TARMAX模型的预测结果。通过与以最高气温为协变量的预测结果相比可以看出：两者的预测误差较为接近，表明平均气温对负荷也有重要的影响。

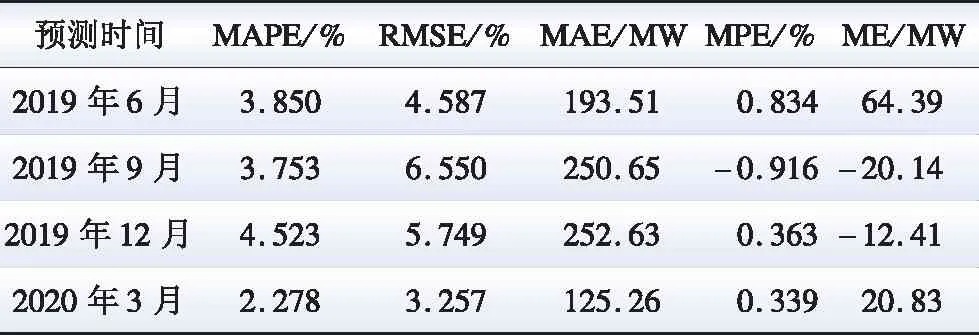
表4 以平均气温为协变量的预测精度

图11为2014年1月到2016年8月浙江省西南某地级市和北京市的月用电负荷-月平均最高气温散点图，月负荷数据由一个月中每日平均负荷数据累加得到。可以看出：北京地区的负荷也存在门限效应，与浙江地区相比，由于地域因素，其门限值小于浙江地区的门限值。所以本文所提方法在北方地区同样适用。

图11 不同地区负荷-气温散点图

4 结 论

本文充分利用气温与居民用电负荷之间的关系，发现了居民用电负荷时间序列的门限效应。针对此类非线性特征，以气温为协变量、气温突变点为门限，建立了非线性TARMAX模型。所建模型克服了传统线性时间序列模型对非线性时间序列拟合的困境；同时，加入了外源因素——气温，进一步提高了预测精度。文中应用MCMC算法搜寻到了气温突变点，反映了居民用电负荷的非线性特征。其次，根据随机搜索变量方法高效地选择出模型系数，提高了算法的实际应用价值。通过实例对不同季节下的居民用电负荷进行了预测。结果表明：TARMAX预测效果优于传统线性时间序列模型、LSTM和MLP，验证了该方法在负荷预测方面的有效性，且能适应气温较大幅度变化。

本文所用算法可以与机器学习、深度学习相结合，构成新的组合模型来进一步提高负荷预测精度；由于在协变量的选择上考虑了气温因素，因此，预测的效果会受到天气预报准确度的影响；同时，在今后的研究中，可以考虑多重气象因素对电力负荷的影响。