基于DFIG功率振荡阻尼器的电力系统低频振荡抑制综述

李生虎，叶剑桥，张浩，陈东，朱争高

(1.合肥工业大学电气与自动化工程学院，合肥市 230009；2.新能源利用与节能安徽省重点实验室，合肥市 230009)

0 引 言

随着电网互联，机组间动态交互加剧，低频振荡(low frequency oscillation，LFO)危险逐渐增加。低频振荡一般指0.1～2.5 Hz间的弱阻尼振荡过程。振荡频率越低，波及范围越大、持续时间越长，可能引发线路保护误动甚至电网解列，国内外已发生多起因低频振荡导致较大范围区域电网故障，产生严重后果和经济损失的实际案例[1]。

近年来，风电等新能源容量快速增加，双馈风电机组(doubly-fed induction generator，DFIG)以控制灵活、经济实惠等特点，得到广泛应用[2]。DFIG结构和控制策略与传统同步发电机(synchronous generator，SG)存在差异。其机械输入由风速决定，可控性弱；没有独立励磁系统，而是通过背靠背变流器控制机端/耦合点电压/功率；没有功角同步需求。由于DFIG和SG间动态交互、DFIG与系统间弱耦合，导致DFIG接入电力系统时会降低系统阻尼，增加发生低频振荡的风险，降低了系统低频振荡稳定抑制能力；同时伴随着大量同步机组被替代，导致系统逐渐弱化(低惯量、低短路比)，“双高”电力系统的宽频带振荡问题也愈发严重[3]。并且电网对并网风电机组的性能要求逐渐从被动跟随电网转变为主动支撑电网，因此更有必要研究风电并网LFO抑制措施。

现有针对DFIG风电并网系统LFO的研究，主要集中在振荡机理、抑制措施和控制设计等方面。

低频振荡起因包括风速快速变化、塔架机械振荡、控制动态交互等，可基于外部监测或内部建模，采用负阻尼、分岔理论等予以分析[4]。站在电网角度，弱阻尼LFO往往源于SG内部控制(励磁系统、调速系统)间动态交互。并网DFIG和SG控制策略相互影响，可能加剧原有LFO或引入新模式。增加硬件或改进软件控制，可抑制LFO。如强化输电网结构可以缓解LFO。SG加装电力系统稳定器(power system stabilizer, PSS)，改进PSS控制策略和控制参数，在高压直流、柔性交流、储能等设备中增加广域控制，也可抑制LFO，其难点在于控制算法和相互协调。

在非峰荷阶段，部分SG被风电替代，SG原有稳定控制策略未必可用。为此可在DFIG上加装功率振荡阻尼器(power oscillation damper，POD)，实现与SG-PSS类似功能[5]。但是如何设计POD控制策略，以适应运行场景变化、与SG-PSS协调，仍需进行深入研究。

现有文献[5-6]对新能源并网系统LFO进行调研，但对LFO影响因素、阻尼控制器分类、控制策略优缺点的探讨，仍较笼统和模糊。本文梳理DFIG对电网LFO的影响，给出抑制措施选择和POD常用设计步骤，按结构固定与否对POD进行分类，探讨POD参数整定和控制策略设计，比较其优缺点，并对接下来DFIG并网电力系统低频振荡抑制研究方向进行展望。

1 DFIG并网对低频振荡影响

DFIG并网对LFO影响的原因包括改变潮流分布、与SG间动态交互等。文献[7]考虑了两者，将DFIG等效为恒功率源来描述其对LFO的影响。DFIG与SG动态交互对低频振荡的影响，可以通过多机场景下阻尼转矩来分析。随后，文献[8]综合潮流变化和动态交互2个因素，分析DFIG对系统稳定性的影响。文献[9]设计了动态指标以量化DFIG和SG动态交互程度，发现风电渗透率加剧了动态交互程度。文献[10]提出LFO模式阻尼比对SG无功出力灵敏度的解析表达，提出了基于无功优化的振荡稳定约束最优潮流模型，以期同时改善电网经济性和稳定性。

文献[11]发现了风电并网引起的新振荡模式：其一是风电变流器结构不同导致；其二是其控制回路与SG动态交互引起，对控制参数敏感。文献[12]参考SG机电模式，根据DFIG机械暂态定义机电回路相关比，确定由DFIG引起的LFO模式；推导LFO模式对DFIG和SG控制参数的灵敏度；发现忽略DFIG并网点电压暂态，将导致LFO结果误差。文献[13]利用阻尼转矩分析多DFIG间动态交互如何影响系统低频振荡，认为相互作用主要影响输入变量，对阻尼回路无影响。风电机组锁相环(phase locked loop，PLL)对电网稳定存在影响[14]。文献[15]认为DFIG容易在重载条件下失去稳定性，LFO振幅和PLL参数相关；为抑制由PLL引起的LFO，提出混合鲁棒阻尼控制器用于DFIG控制。当PLL激发某些振荡模式时，PLL自由响应与系统振荡耦合，将引入负耗散强度项；此时DFIG作为振荡源向电网注入能量，加剧系统振荡，更易失稳[16]。

由于建模精度和假设条件不同，现有研究中出现了一些相互矛盾结论。文献[17]研究变速风电机组通过改变电网潮流影响电网稳定，发现风电渗透率越高，系统阻尼振荡能力越强，但是采用给定功率描述风电出力，忽略风电机组内部结构和控制策略，结论存疑。文献[18]在BPA软件中引入DFIG动态模型，发现当风电渗透率增加时，系统阻尼将减弱，更易发生振荡。文献[19]研究了旋转备用容量对区域电网振荡模式的影响，发现在减少旋转备用容量时，阻尼特性并非单调变化，随渗透率增加，振荡模式阻尼比下降。

实际风电渗透增加对LFO的影响取决于风电机组建模精度、替换SG方式、电网运行场景等，需要具体建模分析，以得到准确LFO模式及有效的抑制方案和最优控制参数。

2 抑制措施选择

2.1 抑制措施比较

抑制LFO措施基本思路是增加系统阻尼，包括SG加装PSS、DFIG控制参数优化、DFIG加装POD、柔性交流输电系统(flexible AC transmission systems，FACTS)和高压直流输电(high-voltage DC，HVDC)加装POD等。各种方法优缺点对比见表1[20-24]。DFIG-POD设计方法和控制策略，将在第3节分析比较。

表1 阻尼控制比较

2.2 POD与PSS比较

PSS作为SG励磁附加输入，提供与转子速度偏差同相的阻尼分量，以维持功角稳定、抑制振荡[25]。PSS控制结构如图1所示。图1中增益环节保证PSS阻尼并补偿信号衰减；隔直环节抑制噪声干扰；超前滞后环节补偿励磁系统和SG电气转矩分量间相位差。文献[21]在DFIG安装附加阻尼控制器(称为DFIG-PSS)，结构和SG-PSS类似。后来为了区分，将风电机组、HVDC和FACTS上的PSS称为POD。

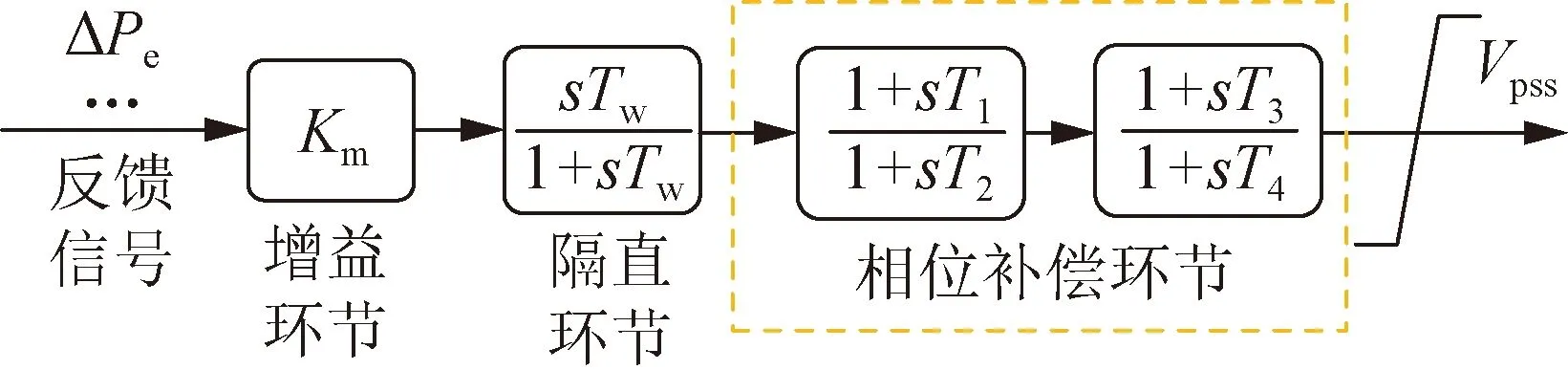
图1 PSS控制结构

3 DFIG-POD设计

图2给出了DFIG-POD控制结构，其设计步骤为：确定POD位置、选择输入信号、整定控制参数。

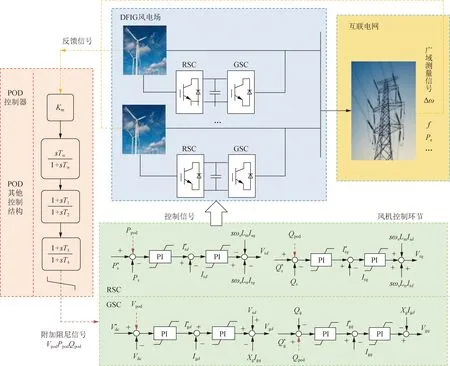
图2 DFIG-POD控制结构

3.1 DFIG-POD安装位置和输入信号选择

按照控制对象，POD可分为有功控制[21]、无功控制[26]和有功/无功混合控制[27]。POD安装在机侧变流器(rotor-side converter，RSC)，可抑制振荡幅值；安装在网侧变流器(grid-side converter，GSC)，可加快振荡收敛速度。

POD是通过控制DFIG出力来增加阻尼。POD控制作用可能加剧DFIG自身振荡，威胁到其稳定性[28]。因此，文献[29]考虑到POD对DFIG的负面影响，引入有关DFIG安全约束，优化POD参数，在抑制振荡同时维护DFIG的运行安全。

POD输入信号通常取与振荡相关的测量信号[30]，如电网频率、SG转速差、SG功角差、联络线有功等。随着广域测量系统(wide area measurement system，WAMS)应用，选取广域信号有助于抑制区域间振荡，但通信时滞影响POD控制效果，可通过设计时滞补偿器[31]和设计时滞不敏感POD[32]等予以解决。

留数法通过计算能控能观性指标选取最佳输入信号，可用于POD输入信号选择。文献[33]针对广域集中和本地控制组成的分层方案，采用留数法选取广域集中控制输入信号，同时优化集中控制和本地控制参数，以抑制系统振荡。文献[34]基于留数法分析POD输入信号在不同运行条件下提供阻尼的变化。留数法只能用于比较同类信号间的能控能观性，特征向量计算量较大。

有学者探讨其他输入信号选择。文献[35]采用POD自适应信号选择方案，在不同工况下根据综合指标选择DFIG-POD输入信号。文献[36]计及POD性能约束，设计最佳输入信号匹配方案。

3.2 DFIG-POD控制策略

DFIG-POD控制策略分为DFIG-POD固定结构的参数整定和不固定结构的控制策略，其分类如图3所示。

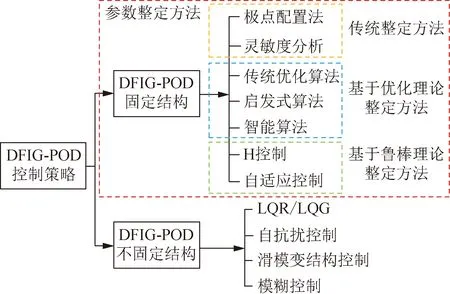
图3 DFIG-POD控制策略分类

3.2.1 DFIG-POD固定结构

针对图1结构，采用传统方法、基于优化理论、鲁棒理论等整定DFIG-POD控制参数。

3.2.1.1 传统整定方法

1)极点配置法。

将系统闭环极点移动到期望的位置上，使得系统性能指标满足要求。但是实际控制中，受系统规模、调节能力、建模不确定、干扰等因素影响，很难配置所有极点，因此采用区域极点配置[37]，常见配置区域有三角型、带型和D型区域。

文献[38]基于根轨迹和极点配置，设计了DFIG附加无功阻尼控制器。文献[39]采用线性矩阵不等式(linear matrix inequality，LMI)进行区域极点配置，增加了弱阻尼模式阻尼比。文献[40]针对含DFIG系统，提出了广域阻尼控制参数寻优方法，建立了阻尼和频率的概率密度函数，根据区域极点配置原理构建目标函数，采用序列二次规划(sequential quadratic programming，SQP)求解。

极点配置法需要考虑系统闭环极点，控制器阶数可能较高，LMI算法对系统规模有限制，因此可能需要对系统进行动态降阶。

2)灵敏度分析。

特征值灵敏度量化参数变化对LFO模式的影响，筛选并调节对关键模式起作用的参数以抑制LFO[41-42]。求解特征值时，摄动法简单但适用性差，解析表达简洁实用但推导难度较大。文献[43]基于特征灵敏度，研究关键控制参数对振荡的影响，建立Hopf分岔边界，给出DFIG参数调整建议。文献[44]计及特征值灵敏度截断误差、优化前后危险模式和有效控制参数差异，采用连续线性规划模型优化DFIG参数。针对特征值分析中忽略参数增量与特征值增量间相互作用，文献[45]在灵敏度中引入参数增量，优化POD参数。考虑一阶特征值灵敏度误差，文献[46]改进特征向量灵敏度算法以避免其多解，建立特征值二阶灵敏度模型用于DFIG-POD控制参数优化。

轨迹灵敏度计算控制参数对系统动态性能指标的影响可用于DFIG参数优化。文献[47]基于轨迹灵敏度分析，定义DFIG中线性二次调节器控制器的加权矩阵Q，通过电压和功率补偿来提高系统阻尼。文献[48]拓展轨迹灵敏度方法，优化DFIG附加频率控制中低通滤波器参数，量化其对系统频率稳定和功角稳定的影响。

3.2.1.2 基于优化理论整定方法

1)传统优化算法。

传统优化算法数学基础完善，编程难度大，但是计算效率高、收敛性好。针对DFIG-POD设计，文献[49]针对区间模式阻尼比，采用SQP算法协调优化PSS和DFIG-POD参数。文献[50]使用DFIG外环控制抑制区间振荡，基于降阶模型设计POD，采用SQP优化控制参数。

2)启发式算法。

启发式算法模仿自然界或生命体行为模式，利用部分信息不断进化得到最优解，具有一定自学习功能，对初始点选取不敏感，可用于阻尼参数优化设计。用于DFIG-POD参数优化的启发算法有粒子群算法[51]、改进果蝇算法[52]、帝国竞争算法[53]等。与传统优化算法相比，启发式算法推导公式和编程工作量小，但是收敛速度慢，易陷入局部最优，不易证明最优性。

3)智能算法。

近年来，强化学习(reinforcement learning，RL)等人工智能算法得到关注。文献[54]利用RL在不同场景和操作条件下自学习能力，解决广域阻尼控制在抑制LFO中通信延迟、反应时间慢等问题。文献[55]将深度RL应用到多机PSS参数整定，以抑制多频振荡。文献[56]采用基于深度确定性策略梯度强化学习优化PSS参数，以提高系统在不同工况下的稳定性。

RL根据所在环境，通过判断自身经历所产生的反馈信息学会自我决策和控制，不需要大量数据训练，对研究对象物理模型不敏感。但是奖励函数复杂、调试困难、算法收敛不稳定、学习速度慢。当出现未知状况时，可能出现决策错误。

3.2.1.3 基于鲁棒理论整定方法

DFIG-POD参数整定通常基于当前方式，考虑运行场景、故障模式变化，基于鲁棒控制的参数整定方法有助于改善DFIG-POD的控制效果。

1)H控制。

H控制广泛用于处理建模误差、不确定性和系统中工作点变化等。在设计POD中，H控制常和极点配置方法一起使用，以保证闭环系统对运行条件变化的鲁棒性[57]。

文献[58]考虑广域信号时滞效应，引入自由权矩阵，设计广域时滞状态反馈鲁棒控制器；结合状态观测器技术，设计广域时滞POD。文献[59]借鉴H控制思想，采用逆输出乘摄动法对系统不确定性建模，协调设计优化DFIG-POD和PSS。文献[60]基于H2/H∞混合控制，优化DFIG-POD参数。文献[61]针对DFIG-POD，考虑时滞及扰动，提出H∞混合灵敏度鲁棒控制方案。

H控制只在给定不确定性范围内保证系统稳定性，不能保证全局稳定；往往只优化某一鲁棒范数；设计控制器阶次较高时，实际应用较难。

2)自适应控制。

自适应控制分为模型自适应控制(model adaptive control，MAC)、自校正控制器(self-tuning control，STC)和参数自适应控制(parameter adaptive control，PAC)等。MAC和STC在广域阻尼控制中较为常用。MAC控制精度依赖于参考模型，对系统辨识精度要求较高。STC更新控制器参数，需要在线识别系统动态，对实时性要求高[62]。文献[63]提出了多模型MAC阻尼控制，采用聚类算法提取模型库，计算模型匹配概率，更新各阻尼控制器输出权重。

文献[64]针对不同工况LFO，提出了DFIG-POD自适应抑制方法。文献[65]计及通信延迟，提出基于数据驱动的自适应控制风电场广域阻尼控制，基于超前加权预测确定补偿时延，引入动态线性化技术处理不确定因素，改善抑制效果。

自适应控制设计存在问题，首先是对在线、非线性模型的辨识精度有限，其次是辨识和校正需要时间，对实时性要求高场合存在控制误差。

3.2.2 DFIG-POD不固定结构

有学者将线性二次型调节器(linear quadratic regulator, LQR)、自抗扰控制(active disturbance rejection control，ADRC)、滑模变结构控制(sliding mode control，SMC)、模糊控制等用于DFIG-POD，以改善其控制性能。此时POD结构和图1不同。

1)LQR控制器。

LQR设计状态反馈控制器K，使得控制性能指标函数J最小，实现系统性能最佳。其优点是通过Riccati方程，解析求解K，易于编程实现。文献[66]将LQR应用于DFIG-POD，将其和FACTS设备协调控制，抑制区域间LFO。考虑实际系统不易写出状态方程，为准确量测，文献[67]采用无迹卡尔曼滤波器估计不可观测状态，基于LQR设计DFIG-POD。

LQR设计效果依赖于系统建模精度。实际系统存在噪声，不易用性能指标精确描述实际情况。当系统规模较大时，需要进行动态等值，影响控制效果。

2)自抗扰控制。

自抗扰控制由跟踪微分器、扩展状态观测器和误差反馈控制组成，结构简单、实时性较高、抗干扰能力强。文献[68]选择广域阻尼反馈信号，基于ADRC设计了广域DFIG-POD。ADRC涉及参数较多；扩张观测器设计较为复杂；当系统阶数较大时，非线性反馈控制律设计困难。

3)滑模变结构控制。

滑模变结构控制对系统参数变化及外界扰动不敏感、实现简单。可通过POD反馈信号设计滑模面函数，再利用趋近率设计控制律，将控制信号引入风电系统[69]。为解决SMC高频抖振问题，改善控制收敛性，文献[70]设计了基于二阶SMC的DFIG-POD以抑制系统LFO。文献[71]提出了基于鲁棒精确微分器和不连续积分器复合的SMC，用于DFIG-POD控制，以避免控制抖振、改善控制效果。SMC的缺点在于理想滑模切换面难以设计；滑动模态到达条件需要严格证明；高频抖振需要用饱和函数来解决，可能影响控制效果和系统稳定。

4)模糊控制。

模糊控制理论通过引入风电反馈信号，如电压误差、有功误差等，采用离线方式制定模糊控制表，输出POD控制器信号[72]，避免了理论建模问题。文献[73]比较了采用3种不同控制策略DFIG-POD对系统阻尼的提升性能，发现相比启发式算法和留数法设计POD，采用模糊控制POD抑制LFO效果更显著。文献[74]为解决阻尼控制中不确定性的影响，基于区间二型模糊集设计了DFIG-POD，在RTDS中进行硬件在环验证。

模糊控制凭经验设计模糊规则及隶属度函数，对于复杂场景适用性一般；不易验证模糊控制系统的稳定性。

3.2.3 DFIG-POD控制策略比较

从鲁棒性、对线性系统模型的依赖性、设计/求解成本、发展情况等方面，比较POD控制策略，如表2所示。

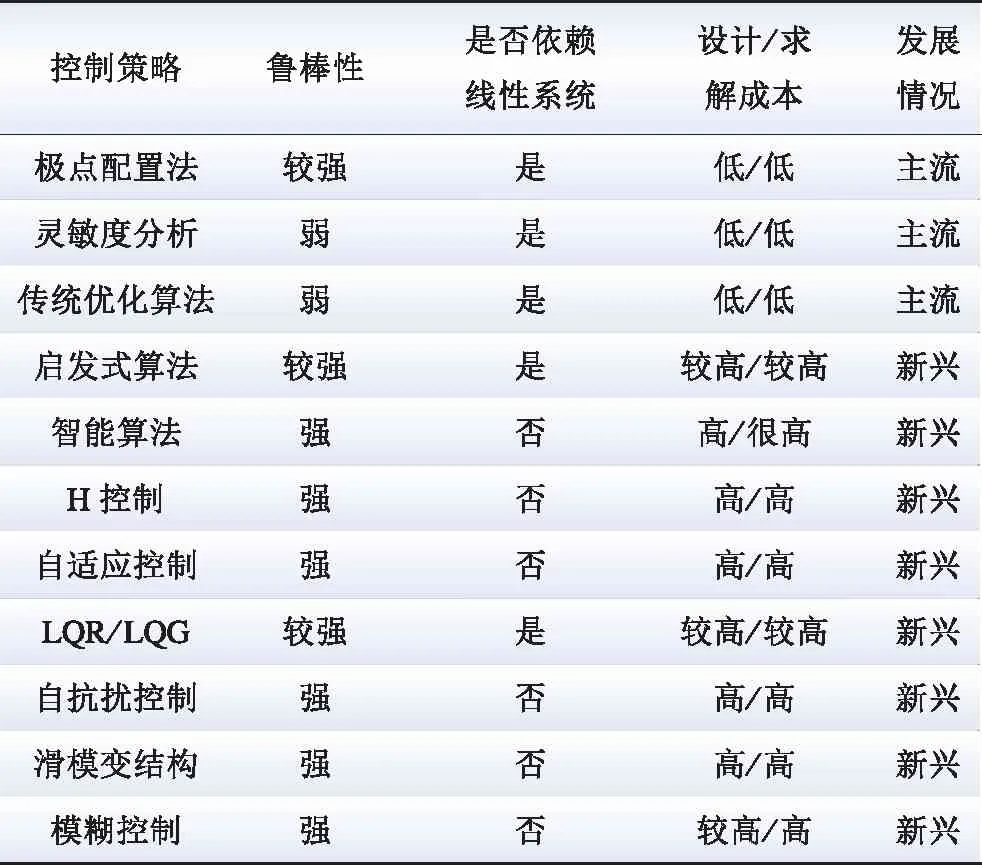
表2 DFIG-POD控制策略比较

极点配置法、灵敏度分析和传统优化算法的求解成本较低，但是应对系统不确定性能力有限。可以结合自适应控制、智能算法、自抗扰控制等优点，设置LFO抑制方案。

4 研究展望

1)完善DFIG对电网低频振荡影响的理论基础和分析方法，辨识振荡中心、明确振荡路径，从而为DFIG-POD安装、设计提供基础支撑。

2)电网中不同控制器的待控制模式、时间尺度、控制策略差异较大，其相互作用可能会弱化LFO抑制效果，因此需要协调控制策略以实现控制效果最优，并减小对设备本体控制的负面影响。

3)DFIG台数远多于SG。从工程计算考虑，往往简化或忽略DFIG间差异、集电网络、场内多DFIG控制交互，将风电场等效成一台DFIG，降低了控制措施可实施性和控制效果精度。

4)DFIG参与电网振荡抑制属于广域控制，需要知道远端设备状态、控制策略和控制参数。自适应控制、人工智能的应用，使得电网控制结构和参数灵活多变，增加了LFO抑制的难度。

5)随着电力市场、实时电价、可调度负荷、虚拟电厂发展，控制需求和控制成本间矛盾日益突出。以价格和效益为杠杆，调度新能源场站和灵活负荷参与LFO抑制，具有较好发展前景。