基于改进梯度提升算法的短期风电功率概率预测

庞传军，尚学伟，张 波，余建明

（1. 南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省南京市 211106；2. 北京科东电力控制系统有限责任公司,北京市 100192）

0 引言

具有间歇性和随机性特点的风电大规模接入电网加大了电网调度运行的难度［1］。对于短期风电功率预测,其预测次日00:00 起72 h 的风电输出功率［2］,预测结果是制定调度运行计划的依据。传统短期风电功率预测以确定性预测（点预测）为主。但是,确定性预测结果不能描述风电功率预测结果的不确定性［3］。含大规模风电的电网运行、安全稳定分析需要考虑风电功率的不确定性对其概率分布进行预测［4-5］。因此,许多学者针对短期风电功率概率预测开展研究,提出了较多的预测方法。

按建模对象划分,包括直接法和间接法。直接法直接预测风电功率的概率分布；间接法先进行确定性预测,再针对误差进行概率建模,然后与确定性预测的结果叠加,形成风电功率概率分布预测结果。按照建模方法划分,包括参数法和非参数法［6］。参数法利用假设的概率分布描述功率/误差的分布,例 如 高 斯 分 布［7］、贝 塔 分 布［8］、指 数 分 布［9-10］、t分布［11］等。当功率/误差不服从假定分布时,参数法会产生较大误差［12］；非参数法不预先假设功率/误差分布的表现形式,通过数据驱动的方法直接计算功率/误差分布函数或分位点。常用的方法包括分位数回归［13］、自适应重采样［14］、核密度估计（kernel density estimation,KDE）［15］等方法。非参数方法不存在假定分布不合理的问题,可以有效避免建模误差［6］,但是使用起来较为复杂［12］。文献［16］详细对比了参数法和非参数法的优缺点。

随着以神经网络为代表的人工智能技术的日益成熟,该技术也被应用于短期风电功率概率预测领域。文献［17］利用小波神经网络,结合KDE方法建立短期风电功率概率预测模型；文献［18］和文献［19］分别采用基于径向基神经网络和长短期记忆网络的分位数回归,实现了风电功率的区间预测。文献［20］则利用基于神经网络的上下限估计和Bootstrap 方法,实现短期风电功率概率区间预测。基于神经网络的风电功率概率预测方法主要有2 种实现方式:1）针对风电功率的不同分位点进行预测,形成预测区间,该方式需要针对不同的分位点分别训练预测模型,然后再利用不同分位点的预测结果拟合出风电功率概率分布；2）先进行风电功率点预测,再对点预测误差的概率分布建模。2 种方式需要两阶段建模,并且概率预测结果依赖于点预测的结果。除神经网络方法外,贝叶斯学习［21］、高斯过程回归（Gaussian process regression,GPR）［22］、极限学习［23］等其他机器学习方法也被应用于风电功率概率预测。 梯度提升（gradient boosting machine,GBM）算法能够防止过拟合,具备较好的泛化能力［24］,并且具有较强的非线性表达能力,能够学习到外部气象因素与风电功率之间的复杂非线性关系［25］。虽然该算法及其相应的改进算法在电力负荷［25］、风电场风速［26］的确定性预测方面取得了较好的预测效果,但是仍然需要采用与神经网络类似的方式才能实现风电功率的概率分布预测,不能直接实现其概率分布预测。鉴于此,本文在分析确定性预测和概率预测之间区别的基础上,提出一种基于改进GBM 算法的短期风电功率概率分布直接预测方法,并在概率分布预测的基础上实现了区间预测。采用实际的风电功率数据对该方法的预测性能进行分析,验证了方法的实用性和有效性。

1 短期风电功率确定性预测和概率预测

1.1 确定性预测和概率预测的定义

短期风电功率预测需要采用数值天气预报（numerical weather prediction,NWP）信息以提高预测精度［27］。因此,通常采用先建立风电功率模型再进行预测的方式,即先利用NWP 中的历史气象数据和风电功率数据训练风电功率模型,再将NWP中气象因素的预测值输入模型预测风电功率。从机器学习的角度考虑,确定性短期风电功率预测根据NWP 中的气象数据对风电功率的期望值进行预测,预测结果是风电功率的一个可能值。预测模型的训练过程是典型的有监督机器学习,如式（1）所示。

式中:P(⋅)为风电功率预测概率分布,即条件概率密度函数；θ为分布参数；S(⋅)为损失函数,可衡量实际风电功率属于预测概率分布P的可能性。

1.2 确定性预测与概率预测的区别

当建模对象为风电功率本身,预测目标为风电功率的概率分布时,确定性预测与概率预测之间的区别如下:

1）损失函数不同。确定性预测模型的目标是最小化以损失函数衡量的预测功率和实际功率之间的偏差。概率预测模型的目标是最小化风电功率实际值和预测的风电功率概率分布之间的差异,通常采用实际风电功率属于预测风电功率概率分布的似然进行衡量,即最大化实际风电功率属于预测风电功率概率分布的似然,实际算法中采用负对数似然（negative log likelihood,NLL）损失函数。

2）预测对象的数量不同。确定性预测仅针对风电功率单个变量训练预测模型。然而,风电功率具有依赖于外部环境条件的异方差特性［28］,如附录A 图A1 所示。受气温、气压、湍流强度等其他外部因素的影响,相同的风速水平下,风电功率在理论出力附近波动；不同的风速水平下,风电功率的波动性不同。假设在相同的气象条件下,风电功率服从正态分布,要直接对风电功率的概率分布进行预测,需要针对均值μ和标准差σ这2 个与外部环境之间具有条件相依性的分布参数,分别训练预测模型。

1.3 基于GBM 算法的短期风电功率确定性预测

GBM 算法是一种有监督集成机器学习算法,该算法通过由决策树构成的弱预测模型不断迭代,以最小化前一轮的预测误差为目标训练强预测模型［24］。通常采用均方根误差或者平均绝对误差作为损失函数衡量预测误差。其核心思想是对于历史风电功率数据和NWP 数据组成的训练数据集,训练若干个弱预测模型,然后通过一定的结合策略形成一个强预测模型［29］。目前,该算法已被应用于风电功率确定性预测领域,并且为了提升确定性预测的性能,一些学者对该算法进行了改进［25,30］。但是,对该算法的改进都是为了提升确定性预测的准确度,利用该算法无法直接实现风电功率概率预测,仍然需要采用间接的方式实现。

1.4 GBM 算法应用于短期风电功率概率预测的方式

目前,可采用2 种间接的方式将GBM 算法应用于风电功率概率预测:1）首先进行确定性预测,再针对误差分布进行单独建模,两者叠加形成风电功率概率预测结果；2）利用分位数损失函数对风电功率不同的分位点进行预测,形成风电功率的概率分布区间［31］。2 种方式都需要进行多次建模,不但会导致训练时间的增长,也会导致预测误差的叠加。

1.5 GBM 算法直接应用于短期风电功率概率预测的问题

如果将GBM 算法直接用于风电功率概率预测会存在以下问题:

1）GBM 算法中采用的损失函数不能反映实测功率和风电功率预测概率分布之间的差异；

2）损失函数在概率分布参数空间计算的梯度,在概率分布空间中并不是最优的参数搜索方向,导致训练模型的过程不能收敛到最优值；

3）GBM 算法针对风电功率单个变量建立预测模型,无法同时针对风电功率概率分布所需的多个参数变量建立预测模型。

2 基于改进GBM 算法的短期风电功率概率预测

2.1 概率预测的NLL 损失函数

短期风电功率概率预测损失函数的输入包括风电功率预测概率分布P和实测功率y,用S(P,y)表示。如果采用参数化的建模方法,损失函数可表示为S(θ,y),其中,θ为预测概率分布P的参数向量。当预测的风电功率概率分布P越接近风电功率真实概率分布Q时,损失越小。因此,在概率分布空间中,损失函数应满足以下特性［32］:

对数似然衡量实测风电功率属于预测风电功率概率分布的似然,预测模型训练过程应以最大化预测概率分布下产生实测功率的似然为目标。最小化NLL 等同于最大化对数似然。利用NLL 作为损失函数,解决了GBM 算法中采用的损失函数不能反映实测功率和风电功率预测概率分布之间差异的问题。

2.2 损失函数自然梯度的定义和计算

GBM 算法的训练过程中,每一次迭代沿着损失函数相对于参数负梯度的方向寻找损失函数的最小值。梯度的方向是参数变化后损失函数上升最快的方向,即

式中:∇S(⋅)为损失函数的梯度；d为参数的变化量；ε为参数变化量的大小；||⋅||表示求范数。

在风电功率概率分布的情形下,GBM 算法中使用的适用于确定性预测的均方根误差或者平均绝对误差损失函数变为NLL。概率分布参数之间的距离并不能代表概率分布之间的距离,即概率分布参数空间中的梯度下降并不代表概率分布空间中的梯度下降。从而导致损失函数不能收敛到最优值。

在概率分布空间中通常采用散度量度距离。对于满足式（3）特性的概率分布空间中的损失函数,式（3）中不等号右侧减去左侧,称为该损失函数在概率分布空间中的散度DS(Q||P)［35］,即

式中:IS(θ)为费希尔信息矩阵（Fisher information matrix,FIM）,定义如下［38］。

FIM 定义了以KLD 为距离量度的概率分布空间中损失函数的曲率［35,38］。FIM 可修正参数空间的梯度,使其转变为概率分布空间中的梯度。实际计算FIM 时,在参数为θ的概率分布上采样进行计算。

2.3 基于改进GBM 算法的短期风电功率概率预测方法

基于NLL 损失函数和自然梯度,对GBM 算法进行改进,称为自然梯度提升（natural gradient boosting machine,NGBM）算法。

算法输入:历史NWP 中的气象数据和风电功率数据D=[xi,yi],其中,xi和yi分别为样本i的气象因素和风电功率；i=1,2,…,n（n为样本总数）；迭代次数为M,学习率为η,损失函数为S,弱预测模型为f,假设在相近的外部环境条件下,风电功率服从参数为θ=[μ,σ]的正态分布N(μ,σ2)。

步骤6:对每一个训练样本i更新参数。

该算法将风电功率概率分布预测问题转换为分布参数的预测问题,可以针对风电功率概率分布所需的多个参数建立预测模型,算法利用NLL 作为损失函数,并利用自然梯度寻找参数在概率分布空间更新的方向,从而提升训练过程中的收敛性能。

2.4 短期风电功率预测区间的计算

基于风电功率预测概率分布,生成置信水平为(1-α)×100%的风电功率预测区间[Lα,Uα],其中:

式中:α为显著性水平；Lα为区间下界；Uα为区间上界；Zα/2为对应的标准分数。

3 算例分析

3.1 实验数据

利用某风电场2014—2018 年NWP 中的历史气象数据和实际采集风电功率数据验证基于NGBM算法的预测模型的收敛性能和预测性能,数据的时间分辨率为10 min。将2014—2017 年数据作为训练集,2018 年数据作为测试集。风电功率受风速、湍流强度、风向等气象因素的影响［29］,因此,预测模型的训练采用如附录A 表A1 所示的气象因素。测试集中包含了训练模型时采用的气象因素的预测值,数据来源为NWP。

3.2 算法设置

为对比分析不采用自然梯度的GBM 算法（仅采用了NLL 损失函数,训练过程没有利用自然梯度）和采用自然梯度的NGBM 算法（采用了NLL 损失函数,训练过程利用自然梯度）的收敛性能。采用相同设置的决策树作为GBM 算法和NGBM 算法的弱预测模型,见附录A 表A2。

假设在相同的气象条件下,风电功率条件概率分布服从参数为θ=[μ,σ]的正态分布,即基于NGBM算法的预测模型中输入的概率分布为正态分布。

3.3 区间预测性能评价指标

采用反映可靠性的平均覆盖率偏差（average coverage error,ACE）和反映敏锐性的预测区间平均宽度（prediction interval average width,PIAW）这2个指标［27］评估基于NGBM 算法的风电功率区间预测方法的性能。ACE 用于评价预测区间的可信程度,其绝对值越小,可信程度越高；PIAW 用于评价预测结果聚集不确定信息的能力,其值越小,能力越强。2 个指标的详细定义见附录A 式（A2）和式（A3）。

3.4 NGBM 算法训练过程的收敛性能

利用NGBM 算法训练集训练预测模型,随着迭代次数的增加,不采用自然梯度GBM 算法和采用自然梯度NGBM 算法时的NLL 损失变化如图1所示。

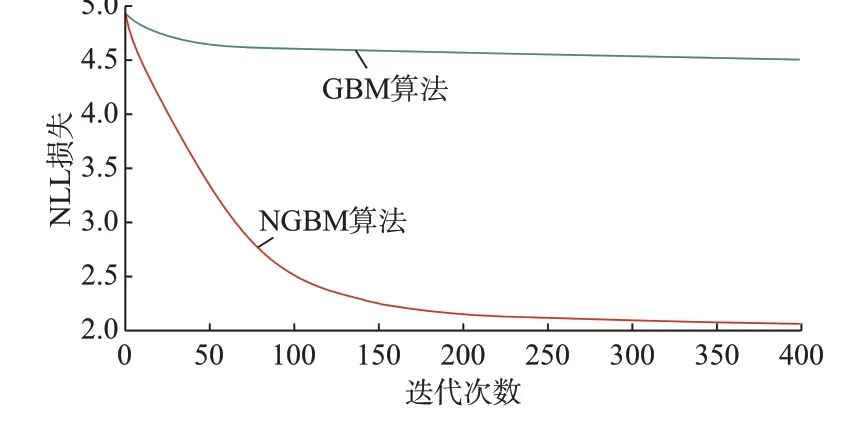
图1 GBM 算法和NGBM 算法随迭代次数增加的NLL 变化曲线Fig.1 NLL variation curves of GBM and NGBM algorithms with increasing number of iterations

由图1 可知,NGBM 算法的NLL 损失下降速度要比GBM 算法快,NLL 损失能够收敛到更小的值。第50 次迭代后,GBM 算法的NLL 损失不再下降。

迭代次数M分别为0、50、100、150 时,在不同的风速水平下,基于GBM 算法和NGBM 算法预测的风电功率概率分布的均值、由式（18）计算的置信水平为95%的预测区间和NWP 中的历史实际风速-功率散点图如图2 所示。

由图2 可知,第50 次迭代到第150 次迭代,采用GBM 算法预测的风电功率概率分布的均值和置信水平为95%的预测区间不再变化。而采用自然梯度NGBM 算法进行预测能够较好地拟合风速-功率之间的关系。由图1 和图2 可以看出,NGBM 算法训练过程的收敛性能要比GBM 算法好。

图2 基于GBM 算法和NGBM 算法在不同迭代次数、不同风速预测的概率分布均值和95%预测区间Fig.2 Mean value of probability distribution and 95%prediction interval based on GBM and NGBM algorithms under conditions of different wind speeds and different iterations

3.5 短期风电功率概率分布预测结果

利用NGBM 算法训练预测模型,对测试集中2018 年1 月1 日至3 日的风电功率概率分布进行预测。将1 月1 日00:00、04:00、08:00、12:00、16:00、20:00 的风电功率概率分布预测结果与实际风电功率概率分布进行对比,结果如图3 所示。需要说明的是,基于数据集中与相应时刻相似的气象条件下的实际风电功率,可利用KDE 方法［15］计算得到实际概率分布。

每日前4 h 的风电功率概率分布预测结果如附录A 图A2 至图A4 所示,每日前4 h 的NWP 中气象因素的值如附录A 图A5 所示。

由图3 可知,预测的概率分布能够近似逼近风电功率的实际概率分布。结合附录A 图A2 至图A4可以看出,在不同时刻、不同气象条件下,基于NGBM 算法预测的风电功率概率分布的标准差不同（概率分布的形状不同）,说明NGBM 算法可以考虑异方差特性实现风电功率的概率分布预测。

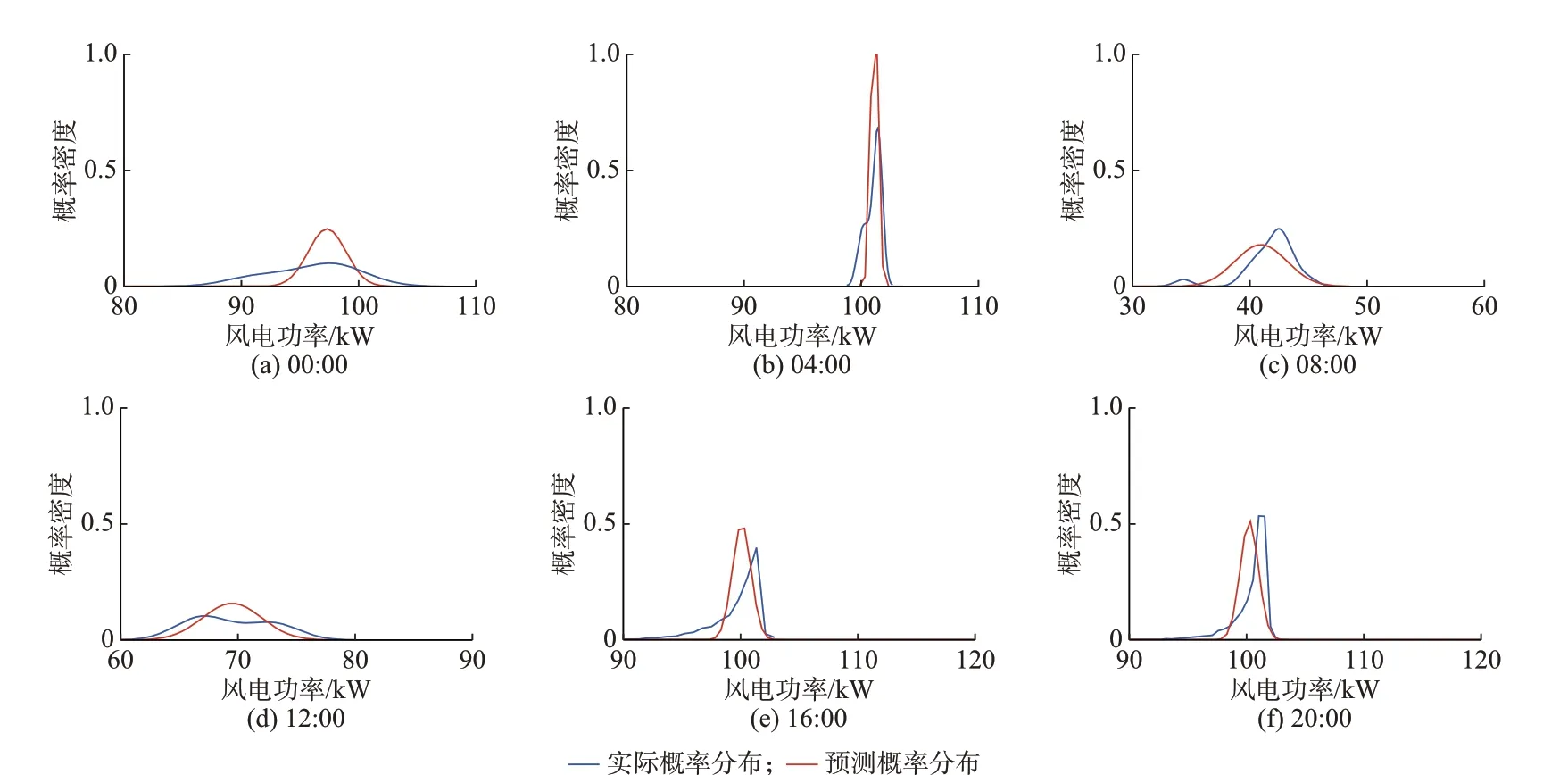
图3 2018 年1 月1 日预测的风电功率概率分布Fig.3 Probability distribution of predicted wind power on January 1, 2018

3.6 短期风电功率区间预测结果

利用NGBM 算法训练预测模型,预测2018 年1 月1 日 至3 日、5 月15 日 至17 日、9 月26 日 至28 日的风电功率概率分布,并将风电功率概率分布的均值作为点预测的结果,然后利用式（18）计算80%、90%、95%预测区间,结果见图4、附录A 图A6 和图A7。

图4 2018 年1 月1 日至3 日基于NGBM 算法的风电功率预测区间结果Fig.4 Results of wind power prediction interval based on NGBM algorithm from January 1 to 3, 2018

由图4、附录A 图A6 和图A7 可知,风电功率的预测区间能够跟踪功率的变化,并且实际功率大部分落在了预测区间之内；随着预测时间的增加,预测区间的宽度逐渐增加,预测结果的不确定性增大。

3.7 风电功率区间预测性能

将基于NGBM 算法的预测方法与基于GBM 算法、梯度提升的分位数回归（gradient boosting decision tree quantile regression,GBDT-QR）算法、GPR 算法、KDE 算法区间预测方法的性能进行对比。根据每种算法在2018 年1 月1 日至1 月3 日的概率分布预测结果,分别计算置信水平为80%、90%、95% 的预测区间,以及预测区间的ACE 和PIAW 结果,如表1 所示。

表1 每种算法在不同置信水平预测区间的ACE 和PIAWTable 1 ACE and PIAW of prediction intervals with different confidence levels for each algorithm

由表1 可知,当置信水平为80%时,GBM 算法的可靠性高于其他几种算法（ACE 绝对值最小）,但是与NGBM 算法相比,其敏锐性较差（PIAW 值较大,区间较宽）,聚集不确定信息的能力较弱。当置信水平为90%和95%时,GBM 和NGBM 算法的可靠性最高（ACE 绝对值都为0）,但是NGBM 算法的敏锐性较好（PIAW 值较小,区间较窄）,聚集不确定信息的能力较强。置信水平为90%时,基于NGBM算法与其他算法的预测区间如附录A 图A8 所示。由图A8 可知,90%置信水平下基于NGBM 算法的预测区间包含了风电实际功率并且宽度较窄,敏锐性较好。

为进一步验证基于NGBM 算法的短期风电功率区间预测性能,分别采用基于以上算法的预测方法对测试集中2018 年全年每天的风电功率概率分布进行预测,并计算50%、80%、90%、95%、98%、99%置信水平下的预测区间,然后在全年的时间尺度上统计每种算法在不同置信水平下预测区间的ACE 和PIAW,结果如图5 所示。

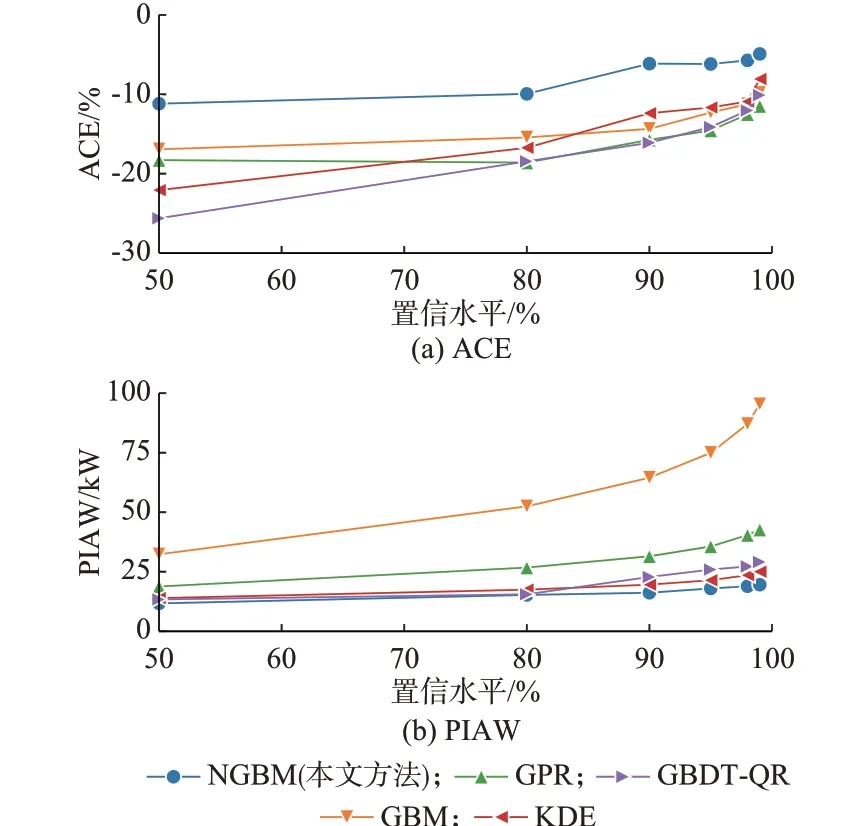
图5 基于NGBM 算法与其他算法的风电功率区间预测性能对比Fig.5 Comparison of wind power interval prediction performance based on NGBM algorithm and other algorithms

由图5（a）可知,从可靠性看,不同置信水平下NGBM 算法与其他几种算法相比,其ACE 的绝对值较小,可靠性较好；由图5（b）可知,从敏锐性来看,不同的置信水平下,NGBM 算法的PIAW 较小,敏锐性较好。综上所述,NGBM 算法能够在敏锐性较好的情况下得到较高的可靠性。

4 结语

本文改进了GBM 算法中的损失函数,并利用FIM 对损失函数在参数空间的梯度进行修正,提出了适用于短期风电功率概率和区间预测的改进GBM 算法。利用实际的风电功率数据对算法进行验证,实验结果表明:

1）采用FIM 修正损失函数在参数空间的梯度后,提升了传统GBM 算法训练风电功率概率分布预测模型的收敛速度；

2）所提算法能够考虑风电功率的异方差特性,预测未来风电功率的概率分布和区间；

3）基于所提算法在风电功率概率区间预测结果的可靠性和敏锐性方面取得了较好的预测效果。

随着贝叶斯深度神经网络等基于深度学习技术的不确定性预测技术的日趋成熟,基于此类技术,利用更多的数据进一步提升风电功率概率预测的性能是未来的研究方向之一。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。