考虑灵活性供需鲁棒平衡的两阶段配电网日内分布式优化调度

赵晶晶，朱炯达，李振坤，张 宇，刘 帅，李梓博

（上海电力大学电气工程学院,上海市 200090）

0 引言

作为电力工业实施能源变革的重要组成部分,分布式电源（distributed generator,DG）在配电网中的渗透率越来越高。DG 一般是指容量小于50 MW、地理上接近负荷侧的分散型发电装置［1］,包括分布式光伏（distributed photovoltaic,DPV）、分布式储能系统（energy storage system,ESS）及微型燃气轮机（micro gas turbine,MGT）等。

含高渗透率DG 的配电网中,DG 规模大、单个容量小且空间分散,采用传统集中调度的配电网调度模型无法满足调度过程中的求解效率要求。因此,配电能量管理系统架构由传统的集中式转变为分布式,决策机制由单一模式转变为自治与协调模式［2］。文献［3］对比了传统集中式调控与分布式调控的优缺点,指出分布式调控具有更优的计算灵活性及计算效率。而实现配电网分布式调控需对配电网进行分布式电源集群（distributed generator cluster,DGC）划分［4］,以可控DG 为控制对象,通过聚合配电网内DG（包括DPV）与负荷节点形成多个控制区域,一个控制区域为一个DGC［5］,使每个DGC 内源荷匹配,从而实现基于DGC 的配电网分布式调控［6］。文献［7-8］分别从降低数学模型维度及最大化新能源消纳角度对配电网进行DGC 划分,并采用交替方向乘子法（alternating direction method of multipliers,ADMM）分别实现了分布式无功优化及经济调度的高效求解,但所采用的DGC划分方法与分布式调度目标耦合性弱,难以充分发挥分布式调度的优势。而DPV 出力的强不确定性对电力系统运行灵活性提出了更高要求,提高配电网的灵活性、有效降低高渗透率DG 接入的不利影响,是近年来国内外的研究热点。

目前,已有学者针对配电网灵活性水平开展研究。在灵活性需求侧,文献［9］考虑风电出力预测误差带来的灵活性需求,建立多时间尺度优化调度模型,提升系统风电消纳水平。在灵活性供给侧,文献［10］提出了电源灵活性裕度指标,通过对灵活性资源进行优化分配有效提升系统灵活性水平,增强风电消纳能力。而配电网灵活性本质上是不同时间尺度下配电网内源荷功率平衡的能力,文献［11-12］建立了配电网多时间尺度调度模型:在日前优化阶段,以1 h 为时间间隔,确定了未来24 h 各机组出力计划；在日内滚动优化阶段,以15 min 为间隔,调整各机组出力计划；在实时调度阶段,根据可再生能源及负荷的实时信息,以5 min 为间隔,采用模型预测控制（model predictive control,MPC）方法,对日内出力计划进行微调,以满足系统实际运行时不断变化的需求。上述研究表明,多时间尺度优化调度方法能够有效消除新能源及负荷预测误差给调度带来的影响,但在日内优化阶段,均采用集中式优化方法,没有考虑大规模DG 接入带来的求解效率低等问题。

本文为消除DPV 及负荷预测误差给调度带来的影响,建立了考虑灵活性供需鲁棒平衡的两阶段配电网日内分布式优化调度方法。首先,在第1 阶段建立了考虑配电网灵活性的DGC 划分方法,对DPV 与负荷日前预测误差产生的灵活性需求进行量化,结合配电网灵活性资源供给能力,提出基于区间覆盖率的DGC 灵活性供需鲁棒平衡指标,并采用改进遗传算法,对配电网进行DGC 划分。然后,在第2 阶段基于同步型交替方向乘子法（synchronous ADMM,SADMM）,以日运行成本最小为目标,提出一种适用于DGC 调控的配电网分布式优化调度模型。最后,以IEEE 33 节点系统为例验证了采用本文所提DGC 划分方法得到的DGC 具有良好的群内灵活性供需平衡能力,所建立的基于DGC 划分的分布式优化调度模型能够实现含高渗透率DG 配电网的高效求解。

1 DGC 灵活性供给与需求模型

1.1 DGC 灵活性需求鲁棒区间

本文考虑配电网调度灵活性,即配电网应对净负荷预测误差（日前预测值与日内预测值存在的误差）所产生的不确定性的响应能力［13］。净负荷即负荷功率与新能源出力之间的差值,因此,配电网调度灵活性来源于新能源出力与负荷功率预测值之间的误差。在电力系统运行中,调度员在日前阶段根据净负荷日前预测数据选择合理的机组启停及出力计划,但由于存在净负荷预测误差,在日内调度时需要具有足够调节能力的发电机组来保证系统的功率平衡。

1.1.1 负荷、DPV 预测误差率分布模型

本文建立负荷、DPV 预测误差率分布模型计算配电网灵活性需求。

1.1.2 DGC 灵活性需求鲁棒区间计算

灵活性需求来源于DPV 及负荷预测的误差,由于存在向上及向下的预测误差,灵活性需求同样存在方向性。本文以鲁棒区间形式表示灵活性需求,区间上界即为最大向上灵活性需求,区间下界即为最大向下灵活性需求。基于1.1.1 节得到的DPV 及负荷向上/向下预测误差率的混合高斯函数,并采用蒙特卡洛抽样法计算灵活性需求鲁棒区间,求解步骤如下:

步骤1:建立预测误差率分布概率模型。基于1.1.1 节,根据负荷及DPV 历史向上/向下预测误差率,进行混合高斯拟合,得到DPV 在各自不同功率区段内及负荷的混合高斯函数,如式（1）所示。

步骤2:建立负荷及DPV 预测场景。针对给定的负荷及DPV 日前预测值,根据步骤1 所得预测误差率分布概率模型及各时刻DPV 出力所在功率区段不同,分别对各时刻负荷及DPV 功率进行向上预测误差率抽样及向下预测误差率抽样,而将最大向上/向下预测误差率场景纳入考虑显然过于保守,因此给定置信水平π,得到预测误差率场景,与各时刻日前预测值累加得到负荷及DPV 预测场景,如式（2）、式（3）所示。

步骤4:建立DGC 灵活性需求场景。净负荷预测误差是灵活性需求来源,DGC 净负荷预测误差场景即为DGC 灵活性需求场景。

步骤5:建立DGC 灵活性需求鲁棒区间。区间方法作为一种有效的不确定性分析方法,仅需要不确定性变量分布区间的大小即可对模型进行求解。根据式（7）、式（8）计算DGC 灵活性需求场景中各时刻DGC 灵活性需求最大值及灵活性需求最小值,得到DGC 灵活性需求鲁棒区间,而步骤2 中的置信水平反映了灵活性需求鲁棒区间的鲁棒性,置信水平越小,所得区间鲁棒性越强,但更趋于保守。

1.2 DGC 灵活性供给区间模型

灵活性供给同样存在向上及向下的方向性。为将配电网灵活性供给映射至与灵活性需求相同的坐标区间,本文同样以区间形式表示DG 灵活性供给能力,区间上界即为最大向上灵活性供给,区间下界即为最大向下灵活性供给。配电网中包含大量可控DG,其中MGT 以及ESS 拥有灵活调节自身出力的特性［16-17］。因此,本文考虑的灵活性资源包括MGT以及ESS,为最大化消纳DPV,本文暂不考虑其灵活调节能力。

ESS 通过放电和充电提供向上、向下的灵活性。在调整ESS 出力时,还需考虑其最大充放电功率限制以及容量限制,其灵活性供给上界和下界分别如式（9）、式（10）所示。

2 两阶段配电网日内分布式优化调度方法

2.1 整体优化调度框架

本文考虑灵活性供需鲁棒平衡能力,提出考虑灵活性并基于集群划分的两阶段配电网日内分布式优化调度方法。在第1 阶段,对配电网进行DGC 划分,为使得到的DGC 群内灵活性供需鲁棒平衡能力最优,需充分发挥DGC 功率自治能力,计算各可控DG 灵活性供给上下界,通过聚合配电网内DG 与负荷节点形成DGC,并将DGC 划分结果传递给第2阶段；在第2 阶段,根据第1 阶段DGC 划分结果,采用SADMM,并以运行成本最小为目标,确定各DG日内最优出力结果。配电网两阶段日内分布式优化调度框架如图1 所示。

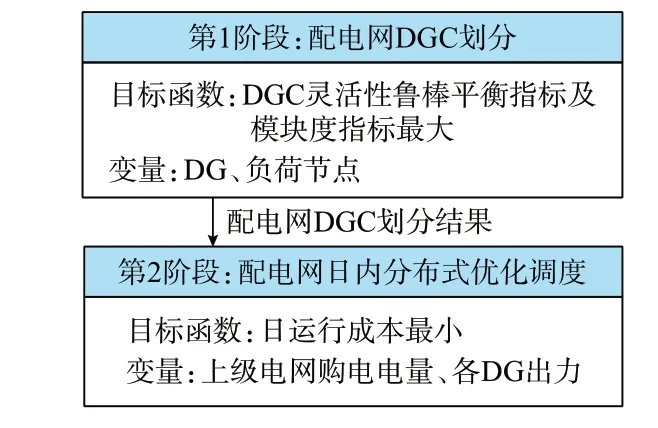
图1 配电网两阶段日内分布式优化调度框架Fig.1 Framework of two-stage intraday distributed optimal dispatch for distribution network

2.2 第1 阶段：考虑灵活性的配电网DGC 划分模型

2.2.1 DGC 灵活性供需鲁棒平衡指标

本文结合DGC 灵活性需求鲁棒区间及DGC 灵活性供给区间,计算DGC 灵活性供需鲁棒平衡区间。如图2 所示,DGC 灵活性供给区间与灵活性需求鲁棒区间的覆盖区间（阴影区域）即为DGC 灵活性供需鲁棒平衡区间,其上下界如式（15）所示。

图2 灵活性供需鲁棒平衡区间Fig.2 Interval of robust balance between flexibility supply and demand

式中:Sbal,c为第c个DGC 灵活性供需鲁棒平衡率,其计算值在［0,1］范围内,越接近于1,则DGC 灵活性供需鲁棒平衡能力越强；T为调度周期。

为对所划分的配电网DGC 灵活性供需鲁棒平衡能力进行整体评估,将各DGC 灵活性供需鲁棒平衡率进行求和并归一化得到灵活性供需鲁棒平衡指标,如式（17）所示。

式中:f为灵活性供需鲁棒平衡指标；NC为划分DGC总个数。

2.2.2 模块度指标

本文采用基于电气距离的模块度指标衡量划分后集群的结构特性。模块度首先由Newman 等人设计提出［19］,以量化社区的结构强度。文献［20］将模块度引入集群划分中,以评价集群划分的结构强度,包括集群内部关联度、集群间关联度、集群个数、集群规模、集群逻辑合理性等。模块度指标越接近于1 代表集群内部联系越紧密,集群间联系越松散。为满足DGC 内部耦合强、外部耦合稀松的特性,以基于电气距离的模块度指标作为集群结构性指标,如式（18）所示。

式中:DQV,mn为节点m、n间基于无功-电压灵敏度系数的电气距离；SQV,mN和SQV,nN分别为节点m和n与配电网中与其相连节点的无功-电压灵敏度系数；N为配电网中节点数量。

2.2.3 DGC 划分模型

为满足DGC 结构性以及功能性,综合模块度指标及灵活性供需鲁棒平衡指标为DGC 划分目标函数,采用线性加权法,将多目标转化为单目标问题。加权目标函数Z如式（21）所示。

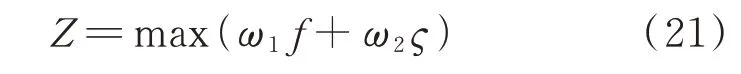
式中:ω1和ω2分别为DGC 灵活性供需鲁棒平衡指标及模块度指标的权重,根据不同目标赋予两个指标不同的权重,且ω1+ω2=1。

采用改进遗传算法对DGC 划分问题进行求解,以邻接矩阵为基础进行染色体编码［20］,保证集群内节点的联通性,采用轮盘赌算法进行个体选择,采用自适应交叉、变异概率算法进行个体交叉、变异,并以上述加权目标函数为适应度评价函数。适用于DGC 划分的遗传算法流程图见附录A 图A1。

2.3 第2 阶段：配电网日内分布式优化调度

2.3.1 适 用 于DGC 的SADMM 算 法

针对传统集中控制难以满足DG 高渗透配电网日内调度时间性能要求的问题,根据DPV 与负荷滚动上报的超短期日内预测数据,采用SADMM,建立基于配电网DGC 划分的日内分布式优化调度模型,以最大限度地消除DPV 与负荷预测误差带来的影响。

为实现基于DGC 的SADMM 算法,首先将配电网各DGC 进行解耦。如图3 所示,i、j分别为相邻的集群i与集群j的边界节点,两个节点通过线路ij相连,其中,根据潮流流向,集群i为上游DGC,集群j为下游DGC。对集群i与集群j进行解耦时,断开联络线ij,在上游DGC 集群i中引入节点j的复制节点j',其作为负荷节点与节点i相连,联络线ij'为集群i的虚拟边界联络线,而在下游DGC 集群j中,引入节点i的复制节点i',其作为电源节点与节点j相连,联络线i'j为集群j的虚拟边界联络线。由此,实现配电网各DGC 之间的解耦。

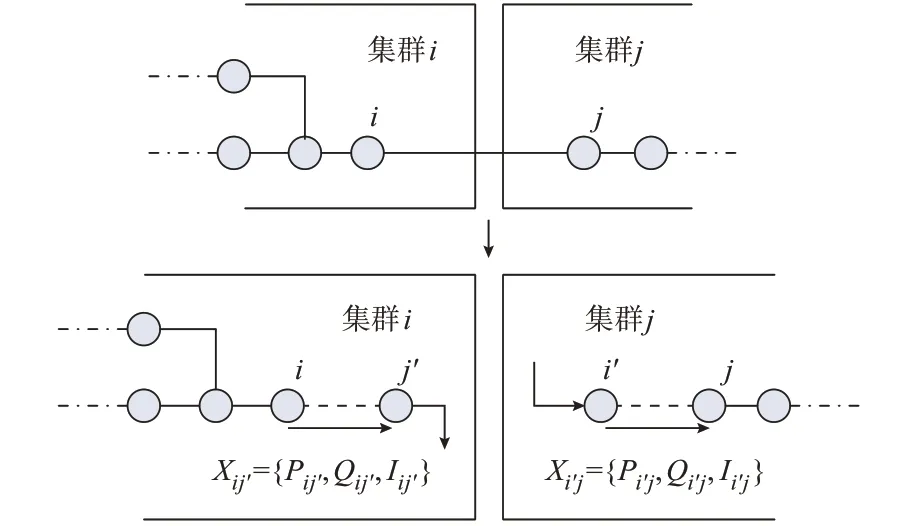
图3 DGC 解耦过程Fig.3 Decoupling process of DGC

在计算过程中,各集群进行独立并行计算,而仅需与各自的上下游集群交换虚拟边界联络线的各变量数据。在传统电力系统潮流计算过程中,变量包括线路有功和无功功率、线路电流以及各节点电压,在配电网中,节点电压与线路有功和无功功率以及电流存在耦合关系,因此,本文设定集群i与集群j虚拟边界联络线的变量为Xij'={Pij',Qij',Iij'}；集群j与集群i虚拟边界联络线的变量为Xi'j={Pi'j,Qi'j,Ii'j}。如此实现配电网DGC 解耦,将配电网整体优化调度模型转化为DGC 优化调度的分布式模型,仅需交互各DGC 少量边界数据,即可实现配电网基于DGC 的分布式优化调度,以减小通信压力、提高计算效率。

在对某DGC 进行优化计算时,将其与相邻DGC 上一次迭代的虚拟边界联络线变量的平均值作为此次迭代过程中的参考值进行计算,如式（22）所示。

2.3.2 日内分布式优化调度模型

本文中,日内优化调度考虑日运行成本最小的经济性目标,并引入一致性成本,DG 包括DPV、MGT 以及ESS。对配电网DGC 进行划分后,建立各DGC 优化调度目标函数如下:

4）MGT 运行约束:MGT 运行约束包括出力上下限约束,如式（33）所示。

式中:us,char(t)和us,disc(t)分别为第s台ESS 的充放电状态0-1 变量,us,disc(t)=1 时处于放电状态,us,char(t)=1 时处于充电状态；Smins和Smaxs分别为第s台ESS 的最大、最小荷电状态（state of charge,SOC）；Es(t)为t时刻第s台ESS 的容量；Es为第s台ESS 的额定容量。

2.3.3 基于DGC 划分的SADMM 计算流程本文基于集群划分的SADMM 计算流程如下:步骤1:初始化拉格朗日乘子,以及各DGC 虚拟联络线变量参考值,初始值为日前调度结果。

步骤2:求解各DGC 优化模型,获取第m次迭代各DGC 虚拟联络线变量值。

步骤3:根据式（27）、式（28）计算原始残差以及对偶残差,判断残差是否满足收敛条件,若满足则结束迭代,输出优化调度结果,否则进入步骤4 计算。

步骤4:根据式（22）、式（25）、式（26）计算第m+1 次迭代各DGC 虚拟联络线变量参考值以及拉格朗日乘子,返回步骤2。

3 算例分析

3.1 算例系统介绍

算例采用包含DG 的IEEE 33 节点系统。系统中DG 接入情况如下:1）18 台DPV；2）10 台MGT、5 台ESS。各类DG 参数及接入节点如附录B 表B1、表B2 所示。

DPV、负荷日前与日内预测值分别如附录B 图B1、图B2 所示。分时电价按北京市工商业分时电价设置［23］,如附录B 表B3 所示,各ESS 运行成本参数为0.083 2 元/（kW·h）［24］,各MGT 出力成本参数为0.85 元/（kW·h）［25］。日前调度以日运行成本最优为目标,日前调度结果如附录B 图B3 所示。算例在MATLAB 2017b 环境下计算,集群划分采用改进遗传算法进行求解,以邻接矩阵为染色体,设定种群数为100,最大迭代次数为500,采用精英保留策略确保算法的收敛性。

3.2 考虑灵活性的配电网DGC 划分

为验证本文所提集群划分方法的有效性,设置了两种集群划分方案:

方案1:只考虑模块度指标进行集群划分,即ω1=0,ω2=1；

方案2:兼顾集群模块度指标以及灵活性供需鲁棒平衡指标进行集群划分,即ω1=0.5,ω2=0.5。

各方案集群划分结果如图4 所示,其中PV 代表该节点接有DPV,S 代表该节点接有ESS 设备,G 代表该节点接有MGT。

根据划分结果可以看出,方案1 仅考虑模块度指标,划分后DGC 数量最多,结构性能更强；而方案2 兼顾模块度和灵活性供需鲁棒平衡指标,将配电网划分为4 个集群,结构强度稍弱于方案1,各集群内所含可控DG 数量相当。

各方案集群划分指标结果如表1 所示,各方案DGC 灵活性鲁棒供需平衡区间如图5、图6 所示。

根据表1 模块度指标结果可以进一步发现,各方案模块度指标结果与其划分结果一致。方案1 模块度指标结果最优,即所划分集群结构性能最强；方案2 模块度指标结果虽弱于方案1,但仅存在较小差距。

根据表1 中各方案DGC 灵活性供需鲁棒平衡指标及图5 可以发现,方案1 虽具有最优的结构性能,但各DGC 的灵活性供需鲁棒平衡能力有较大差异,集群④的灵活性供需鲁棒平衡能力为0,无法充分发挥各DGC 的功率自治能力。而方案2 划分得到的各DGC 在具有较优结构性能的同时,各DGC灵活性供需鲁棒平衡指标均较优,都达到0.7 以上,各集群都具有较强的群内功率自治能力。

图5 方案1 划分集群群内灵活性供需鲁棒平衡区间Fig.5 Interval of robust balance between flexibility demand and supply within cluster of scheme 1

表1 各方案集群划分指标结果Table 1 Results of cluster partitioning index of each scheme

综上所述,本文提出的配电网DGC 划分方法通过结合DGC 灵活性供需鲁棒平衡指标以及模块度指标,寻求配电网最优DGC 划分结果,划分得到的DGC 在拥有较优结构性能的同时,能最大限度地满足各集群内部的灵活性供需鲁棒平衡,充分发挥DGC 群内功率自治能力。

3.3 配电网日内分布式优化调度

为验证本文SADMM 分布式算法的有效性以及在求解性能方面的优势,分别对采用传统集中式与分布式的日内优化调度进行算例分析。

基于DGC 划分方案2 所得结果的分布式优化调度结果见图7,系统总调度成本为30 303.89 元。集中式优化方法得到的系统总调度成本为30 241.63 元,分布式优化方法与集中式优化方法所得到的系统总调度成本误差率仅为0.2%。

图7 日内分布式优化调度结果Fig.7 Result of intraday distributed optimal dispatch

图8 所示为集中式优化方法和分布式优化方法计算收敛曲线。从图中可以看出,经过9 次迭代,分布式优化方法逐步与集中式优化方法结果趋于一致,在求解效率方面,集中式优化方法耗时188 s,而分布式优化方法经过9 次迭代后共耗时676 s。考虑到本文在单台电脑优化计算为串行计算,实际并行计算环境下,分布式优化方法各DGC 平均求解耗时为676 s/4≈169 s,较集中式优化方法减少了10.2%。由此可见,分布式优化方法较集中式优化方法在求解效率方面具有显著优势。

图8 SADMM 及集中式优化收敛曲线Fig.8 Convergence curves of SADMM and centralized optimization

为分析集群划分结果对分布式优化调度的影响,对基于DGC 划分方案1 和方案2 的DGC 划分结果的分布式优化调度进行比较。

基于方案1 的分布式优化方法计算得到系统总调度成本为30 339.41 元,误差率为0.3%。计算效率方面,图9 所示为基于方案1 的分布式优化方法计算收敛曲线。从图中可以看出,方法经过15 次迭代收敛。基于方案1 的分布式优化方法共耗时1 080 s,并行计算环境下,各DGC 平均求解耗时为1 080 s/6≈180 s。对比基于方案1 的分布式优化方法与基于方案2 的分布式优化方法,基于方案1 的分布式优化方法计算误差略有增加,且求解时间增加了6.6%,这是因为方案1 在DGC 划分时仅考虑模块度指标,将配电网划分为6 个DGC,SADMM算法求解时所需交互的虚拟边界变量更多,收敛速度变慢。

图9 方案1 的SADMM 及集中式优化收敛曲线Fig.9 Convergence curves of SADMM and centralized optimization of scheme 1

为比较不同划分方案得到的DGC 的灵活性及功率平衡自治能力,对日内与日前DGC 间功率交互变化量ΔPint进行分析,ΔPint为日内与日前优化调度结果得到的DGC 间功率交互量的差值。DGC 间功率交互变化量ΔPint如图10 所示。

由图10 可见,在DPV 出力高峰期,各方案下DGC 间功率交互变化量ΔPint均发生较大变化,方案1 划分出的DGC 的ΔPint波动性比方案2 更大,这表明方案2 同时考虑模块度和DGC 灵活性供需鲁棒平衡,相较于方案1 仅考虑模块度划分出的DGC,其灵活性及功率平衡自治能力更强。

图10 各方案日内与日前DGC 间功率交互变化Fig.10 Intraday and day-ahead changes in power interaction between DGCs of each scheme

4 结语

本文考虑DPV 及负荷预测误差带来的灵活性需求,以及集中式调度方法难以满足日内调度求解时间性能的问题,提出了两阶段配电网日内分布式优化调度方法。通过算例分析,得出以下结论:

1）在配电网DGC 划分阶段考虑灵活性供需鲁棒平衡指标,可以合理分配配电网灵活性资源,各DGC 不仅拥有较优的结构性能,而且具有较强的功率自治能力；

2）在日内调度中,采用基于集群划分的SADMM 算法能够在保证计算结果有效的前提下,提升计算效率,实现DG 高渗透配电网的高效求解。

本文所提的考虑灵活性的配电网DGC 划分方法以及分布式调度方法均以日内优化调度为研究目标,针对日前优化调度的配电网DGC 划分方法以及分布式调度方法将是下一步的研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。