考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度

胡俊杰，赖信辉，郭 伟，张逾良，杨 烨

（1. 新能源电力系统国家重点实验室（华北电力大学）,北京市 102206；2. 国网河北省电力有限公司经济技术研究院,河北省石家庄市 050011；3. 石家庄通合电子科技股份有限公司,河北省石家庄市 050000；4. 国网电动汽车服务有限公司,北京市 100052）

0 引言

随着电动汽车数量的不断增加［1］,大规模电动汽车接入电网进行无序充电,会给电网带来网损增大［2-3］、电能质量下降［4-5］、电网运行优化控制难度增加［6］等问题,在当前新能源消纳问题严重的情况下,对电网的安全稳定运行构成了很大威胁。因此,需要对电动汽车充电进行优化和引导。电动汽车虚拟电厂（electric vehicle virtual power plant,EVPP）可以将单个容量小、数量众多、随机性较强的电动汽车统一聚合起来进行调配和控制,以向电网提供足够的灵活性［7］,使电动汽车在满足用户出行要求的情况下进行有序充放电,减小电网的负荷峰谷差,促进新能源消纳。在有效限制电动汽车无序充电对电网产生影响的同时,提升电动汽车用户的经济效益。

在电动汽车与新能源协同优化调度领域,文献［8］建立了风电、火电以及电动汽车鲁棒双层随机优化调度模型,但该模型仅考虑了火电机组运行成本,未考虑系统多主体的成本优化。文献［9］以成本最低为目标函数,建立了含电动汽车的虚拟电厂鲁棒对偶模型,但未考虑新能源消纳问题。文献［10］以跟踪光伏功率信号为目标,提出一种电动汽车调控凸优化模型,并在实时调度中滚动优化控制,但缺少对光伏功率的预测。文献［11-13］对电动汽车与风电进行了协同优化,但均未考虑日前风电预测误差所带来的实时调度误差,也未对风电预测误差进行平抑。在风电、光伏以及负荷模态分解预测领域,文献［14］提出了一种基于完全集成的经验模态分解（ensemble empirical mode decomposition,EEMD）和广义回归神经网络光伏电站短期出力预测方法,但由于EEMD 会带来分解误差,对其最终预测结果会产生一定影响。文献［15］提出了一种自适应噪声完全集成的经验模态分解（complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN）、长 短 期 记 忆（long short-term memory,LSTM）神经网络以及样本熵结合的短期电力负荷预测方法,并在算例中分析了其与EEMD相比的优越性。

综上,虽然目前在电动汽车与新能源协同优化调度领域方面的研究已有不少成果,但现有研究并未解决实时调控时预测误差带来的电力系统不平衡问题。

针对上述问题,本文提出了一种考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度方法,以解决风电和基础负荷难以精准预测而导致的实时调控准确度下降的问题。本文所提方法对风电及基础负荷历史数据进行CEEMDAN 处理,并通过双向长短期记忆（bi-directional long short-term memory,BiLSTM）网络算法对不同频率的本征模态分量（intrinsic mode functions,IMF）进行重构预测,并将预测数据用于日前-日内实时模型中。在日前优化中,求解混合整数非线性规划（mixed-integer nonlinear programming,MINLP）模型,得到日前火电机组出力曲线。在日内实时模型预测控制（model predictive control,MPC）模型中,利用电动汽车的充放电灵活性,对当前时刻到未来某时刻的风电与负荷功率预测误差进行实时优化,以维持功率平衡。最后,通过算例仿真验证了本文方法的有效性。

1 方法架构及体系

本文方法的研究对象主要包括3 部分:含风电接入的区域电网、EVPP 以及电动汽车。方法架构如图1 所示,电动汽车通过具有车辆到电网（vehicle to grid,V2G）功能的充电桩接入区域电网,EVPP 通过采集用户侧的电动汽车出行信息和电池荷电状态（state of charge,SOC）对电动汽车进行聚合,并统一调度。区域电网则根据历史相关数据,预测基础负荷与风电功率曲线,同时,在日前得到火电机组出力参考曲线并下发给EVPP,EVPP 据此在日内对电动汽车进行实时调控,并制定每辆车的充放电计划,平抑负荷波动并改善风电消纳问题。

本文所提出的方法流程图如图2 所示。在日前阶段,首先进行风电和基础负荷数据的预测,通过CEEMDAN 分解得到不同频率的IMF 和残差余量,并依据分量极大值个数对分量进行高频、低频及趋势分量重构,重构后采用BiLSTM 预测下一日的风电和基础负荷功率,日前以平抑等效负荷波动与系统成本最优为目标进行优化,求解MINLP 模型,得到优化完的日前火电机组出力曲线。

图2 调度方法流程图Fig.2 Flow chart of scheduling method

在日内调度阶段,设置优化窗口长度为H=4,在读取t时段之前的历史数据后,利用CEEMDANBiLSTM 得到t时段对预测域（未来若干时间段）的风电和基础负荷预测结果。在得到日内预测数据后,将其导入日内调控模型,对预测域［t,t+H-1］的MINLP 模型进行求解,得到［t,t+H-1］的电动汽车调整功率及弃风功率。在t时段求解完成后,仅采用当前时段的功率,不采用预测域未来H-1个时段的功率,完成t时段的优化过程。在t+1 时段,由于t时段的实际风电和基础负荷已知,更新历史数据,进行新一轮的CEEMDAN-BiLSTM 预测及MPC 过程。当t>96-H时,一日的系统调度优化过程结束。

2 基于CEEMDAN-BiLSTM 的风电和基础负荷预测模型

CEEMDAN 是一种从经验模态分解（empirical mode decomposition,EMD）方法改进而来的信号分解方法,由Torres 等人提出并被广泛应用于自适应非线性和非平稳信号的处理［16］。然而,在EMD 执行过程中,会产生端点效应、模态混叠［17］等问题,从而造成IMF 误差较大。EEMD 在EMD 的基础上加入多组恒定标准差的白噪声,以减轻模态混叠带来的影响,但是其分解结果仍无法很好地消除白噪声,导致重构误差较大。CEEMDAN 有效解决了模态混叠以及IMF 白噪声残留问题,提高了信号分解的准确性。

由于风电、负荷等存在非线性且波动较大,难以被精确预测,本文采用CEEMDAN 对风电和基础负荷历史数据进行分解处理,通过自适应分解得到其在不同时间尺度上的周期性特征,以便采用BiLSTM 网络进行预测。CEEMDAN 算法实现过程可参考文献［16］。

在经过CEEMDAN 后,风电和基础负荷数据被分成了若干个IMF 和1 个残差分量。由于经过CEEMDAN 后的IMF 数目过多,为了降低多次预测求和后造成的误差累积并减少模型的计算时间,本文对分解后分量进行重构。如图3 所示,通过计算每个分量的极大值个数,将极大值个数落在统一区域的分量进行重构叠加,生成高频、低频与趋势分量。图中,num,H为高频与低频分量极大值个数边界；num,L为低频分量与趋势分量极大值个数边界；IMF1,IMF2,…,IMFK分 别 表 示 第1,2,…,K个IMF；R为余量。

图3 IMF 重构叠加Fig.3 Reconstruction and superposition of IMFs

由于这些分解后的信号周期性特征明显,重构后使用BiLSTM 算法预测再求和,可以更准确地预测风电和基础负荷数据。BiLSTM 由前向LSTM和后向LSTM 组成,其可以很好地处理序列时间步间的双向长期关联性［18］,挖掘时序数据内部的抽象特征,提升网络时序预测的能力［19］。

在通过CEEMDAN-BiLSTM 预测得到高频、低频以及趋势分量的未来输出后,可以通过求和得到风电和基础负荷预测信息,并将其作为系统调度方法的预测域信息；在日前阶段得到火电机组出力曲线,日内则在滚动优化中实时更新预测结果。

3 区域电网多时间尺度调度模型

3.1 日前优化模型

在日前优化中,为了降低风电及电动汽车并网带来的不利影响,根据预测的风电和基础负荷信息,考虑等效负荷曲线峰谷差及标准差加权和,同时考虑火电机组运行成本、弃风成本,对下一日进行多目标优化,得到下一日火电机组出力曲线。优化以日为周期,单位时段时长为15 min,共96 个时段。

3.1.1 日前调度目标函数

日前调度的目标在于降低等效负荷波动,缓解风电波动对于区域电网造成的压力；对负荷的波动进行控制,使负荷运行更加平稳,同时,提高电力系统运行的经济性。负荷曲线峰谷差及标准差加权和如式（1）至式（6）所示。

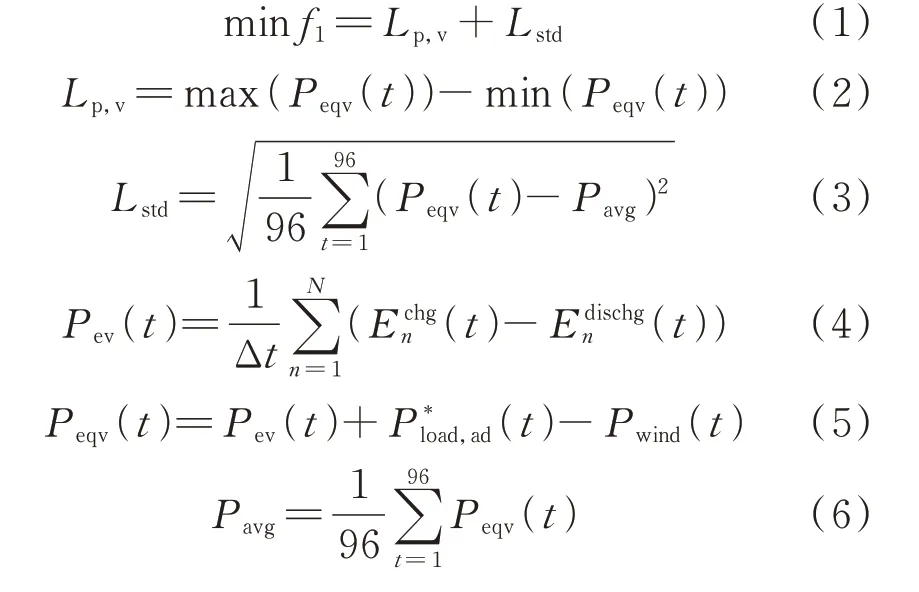
式中:t=1,2,…,96；f1为日前等效负荷平抑目标；Lp,v和Lstd分别为负荷曲线峰谷差和标准差；Peqv(t)为t时段包括电动汽车负荷、风电功率与基础负荷的等效负荷；Pavg为等效负荷平均值；N为电动汽车数量；Pev(t)为t时段所有电动汽车的总净充放电功率；Echgn(t)和Edischgn(t)分别为第n辆电动汽车在t时段的充电电量、放电电量；Δt为优化时间尺度,在本文中取为15 min；P*load,ad(t)为日前预测的t时段基础负荷功率值,基础负荷为除了电动汽车负荷之外的所有负荷；Pwind(t)为风电在t时段的实际功率。

在日前调度阶段,不仅要考虑到系统的等效负荷平抑目标,也要考虑系统的运行成本。本文日前阶段考虑的运行成本由2 部分组成:火电机组运行成本与弃风成本,如式（7）至式（9）所示。

在进行优化调度时,还需要满足电动汽车出行约束条件。当电动汽车接入区域电网进行充放电时,为了减少电动汽车电池损耗,以及保证用户在突发出行需求时仍保有一定的电量,电动汽车的SOC需要满足最大值和最小值约束。同时,在电动汽车离场前,其车辆的电池应尽量达到目标SOC 值,具体可描述成式（17）至式（19）的形式。

3.2 基于MPC 的日内实时调控

在日前优化过程中,由于风电受实时的气象因素影响比较大,在进行预测时,可能会出现部分时间点预测误差较大的情况,所以本节基于MPC 理论在日内实时阶段对电动汽车进行控制,以降低负荷和风电预测偏差带来的等效负荷波动以及系统不平衡问题。

图4 基于MPC 的滚动优化模型Fig.4 Rolling optimization model based on MPC

3.2.1 日内调控目标函数

在日内调控阶段,目标为在保持日前优化得到的火电机组出力不变的情况下,减少弃风成本以及失负荷成本。日内滚动优化的目标函数如式（20）至式（22）所示。

式中:f3为日内优化总成本；Cwind,day为日内实时优化的弃风成本；P*wind,day(τ)为日内实时预测的τ时段风电功率预测值；Cload,day为实时失负荷成本；ΔPloadloss(τ)为实时失负荷量；Sl为单位失负荷成本。

3.2.2 日内调控约束条件

在日内实时调度过程中,除了满足功率平衡约束与电动汽车电量约束外,考虑到日内系统实时平衡以及车主预计离开时间可能会提前的情况,为避免用户出行受到影响,在距预计离开时间3 h 内增加约束条件:

式中:M为当前时段距离预计离开时段长度,M=1,2,…,12；Soc,set(M)为在距离离开时间M时段时电动汽车需要满足的SOC 值。其余约束条件与日前优化相同。

在信息化教学环境下，教师要合理利用网络资源，帮助学生强化自主学习，提升计算能力。其一，自主操作。教师先给学生提出明确的学习任务，并引导学生在有着海量信息的信息化环境中进行资源筛选，借助上网查询、人机交互等方式，让学生亲自动手操作完成，培养学生判断、整理、归纳、加工数学信息的能力。其二，合作共赢。传统的数学教学鲜少有群体活动，而在信息化环境下，教师有了更多的时间和机会开展丰富多彩的群体活动，培养学生的合作能力。例如，教师可通过网络把分散在课堂中的学生链接成小组性的学习团体，并向他们传递声音、文本、图片等各种符号，引导他们进行彼此间的合作，共同面对数学难题，最终实现计算能力的提高。

综上,针对日前目标函数,本文采用Tchebycheff 逼近法［20］对多目标问题进行求解。该方法也是一种权重法,其将多目标拆分成单目标,通过减少目标函数值与理想值之间的最大差距,使模型的解逼近帕累托最优前沿,从而避免使用直接加权求和而导致无法找到非凸函数最优解的问题,故将目标函数重构为式（24）至式（26）的形式。

4 算例分析

4.1 参数设置

本文采用2020 年某区域电网的风电数据,包含功率、风速、风向等特征,以及基础负荷数据,并用高斯分布产生电动汽车到达时间、离开时间和初始SOC 值。电动汽车数目N=300,任意第n辆电动汽车抵达时间tn,arr和预计离开时间tn,dep分别满足高斯分布tn,arr∼N(5,1)和tn,dep∼N(80,1)。设置任意第n辆电动汽车抵达时的初始SOC 满足高斯分布Soc,n,arr∼N(0.5,0.1)。

设置单位调控时段为15 min,火电机组最大和最小技术出力分别为16 MW 和4 MW,向上的爬坡率和向下的爬坡率均为0.16 MW/min,机组运行成本系数a、b、c分别为0.001 2 元/（MW2·h）、0.287 元/（MW·h）、4.073 元/h,煤炭价格为500 元/t；风电单位上网电价为0.6 元/（kW·h）,单位失负荷成本为4 元/（kW·h）；电动汽车的电池容量为60 kW·h,最大充电和放电功率均为20 kW,电动汽车的充电和放电效率分别为0.95、0.92；为保证用户的出行需求,设置用户期望离开时最低SOC 值为0.5；为避免电动汽车深度充放电带来过度电池损耗,在调控过程中电动汽车最小和最大的SOC 分别设置为0.1、0.9。

4.2 风电和基础负荷预测结果

风电和基础负荷分解结果如附录A 图A1 和图A2 所 示,IMF 极 大 值 点 个 数 如 附 录A 图A3 所 示,重构结果如附录A 图A4 和图A5 所示。

在重构得到风电和基础负荷的高频、低频、趋势分量后,针对20 d 的历史数据,取前70%数据作为训练集,后20%作为验证集,后10%作为测试集,用BiLSTM 算法对3 个分量进行单独预测,最后叠加得到预测结果,日前预测时不使用下一日实际值更新训练数据,日内预测时则使用日内实际值更新训练数据,结果如附录A 图A6 所示。可以看出,CEEMDAN-BiLSTM 针对风电和基础负荷的预测均能达到较高准确度。由于负荷规律性较为明显,日前和日内的负荷预测结果相差不大,而风电由于受风速、风向等气象因素影响波动性大,在日前预测时存在一定的偏差,在日内预测时偏差较小。具体结果如附录A 表A1,以及图A7 至图A9 所示。

4.3 模型调度结果

4.3.1 不同权重对日前优化结果的影响

在日前优化过程中,采用不同权重的多目标优化求解结果会不一样。附录B 图B1 展示了不同权重下日前等效负荷优化的对比结果。原始等效负荷为电动汽车在无序充电下且风电不弃风时的等效负荷。表1 展示了不同权重下等效负荷波动指标以及系统成本的对比结果。可以看出,日前优化在w1发生变化时,处于平均等效负荷值以上的负荷“峰”基本不发生变化,优化的部分主要是处于平均等效负荷值以下的“谷”,这是因为在“谷”时段易出现大量弃风,故在权重w1和w2变化时主要会优化“谷”时段的弃风与火电机组出力。

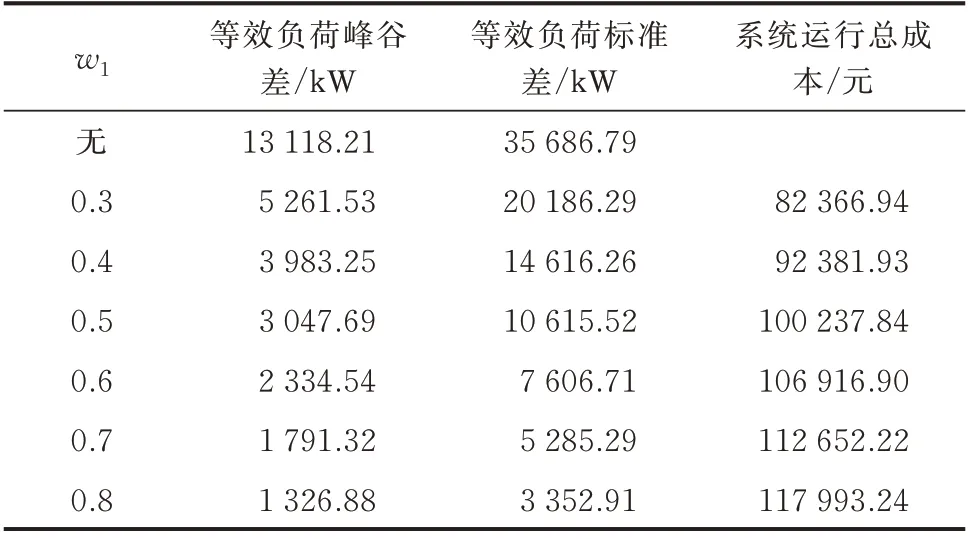
表1 等效负荷波动指标与系统成本对比Table 1 Comparison of equivalent load fluctuation index and system cost

在日前优化平抑等效负荷波动的同时,弃风量也会随着权重取值的不同发生变化。风电在日间得到了较好的利用,基本不会发生弃风情况。为了维持等效负荷波动处于较小的水平,在夜间高弃风量时段,随着目标函数f1的权重降低,在等效负荷波动限制要求不高时,日前优化的弃风功率也逐步降低（见附录B 图B2）。

4.3.2 日内滚动优化效果分析

为了充分验证本文方法在日内实时调控阶段对平抑负荷波动与促进风电消纳的有效性,本文考虑4 种风电功率场景进行研究,如附录B 图B3 所示。

选取权重w1为0.5,求解4 种场景下的日前、日内实际弃风量对比情况,如图5 所示。与日内相比,由于日前对于风电预测的误差较大,在经过实际风电、负荷功率修正后,日前的弃风量会进一步增加,而日内通过MPC 能很好地降低弃风量。由于电动汽车容量限制,EVPP 在日内滚动优化过程中,随着消纳的风电功率增加,电动汽车的SOC 也逐步增加。在EVPP 容量未饱和时,如在场景3 和4 中,日内优化得到的弃风量可以控制在很小的范围内,即EVPP 容量足以消纳场景3 下的弃风量；在EVPP 容量基本饱和后,日内的弃风量会有一定程度的增加,如在场景2 下时段72 至84 阶段日内优化弃风量高于日前,但总体弃风量仍相较于日前发生了大幅降低。表2 展示了在实际情况修正后,本文方法与不采用滚动优化方法的弃风对比结果。

图5 修正后的日前和日内优化弃风情况对比Fig.5 Comparison of day-ahead and intraday wind curtailment conditions after modification

表2 不同场景下弃风结果对比Table 2 Comparison of wind curtailment results in different scenarios

在采用基于MPC 的滚动优化方法后,由于预测模型的加入,提高了日内功率预测的精确度,降低了日前风电预测误差带来的额外弃风量,同时,由于优化时间窗口缩短,求解速度也大幅提高,与不采用滚动优化方法相比更具优越性。

4.3.3 电动汽车调控结果分析

取场景1 进行分析,在经过日内92 轮滚动优化后,可以得到电动汽车的充放电曲线。随机抽样出编号为13、118、201 的3 辆电动汽车,其充放电结果如附录B 图B4 所示。

由于日前优化的时间尺度较长,电动汽车功率较为连续且集中,一般在入场后一段时间普遍进行大规模放电,以满足平抑负荷的需要；在电动汽车即将离开时,则开始陆续充电以满足SOC 设定值。在日内由于采用1 h 时间窗口的滚动优化方式来维持实时功率平衡,电动汽车的充放电功率比较少,且充放电转换频率较日前优化明显增多。日前优化提供的瞬时EVPP 灵活性低于日内优化,这是因为在整日时间尺度上进行优化时,EVPP 的灵活性被分散到了多个时段,而在日内滚动优化时,当某一时段需要EVPP 提供足够多的灵活性时（风电功率较大时）,EVPP 会瞬间释放大量功率以维持实时功率平衡（见附录B 图B5）。采用本文方法,日内EVPP 可提供的瞬时最大放电功率超过1.7 MW,瞬时最大充电功率超过3.5 MW。

附录B 图B6 展示了本文方法在不同电动汽车数量下的风电消纳效果。在不同数量的电动汽车参与下,风电弃风情况均得到了改善,且随接入的电动汽车数量的增多,EVPP 可调控的灵活性越大,日内实时优化阶段对风电消纳的效果越好,其中,当电动汽车数量达到1 000 辆时,在场景1 下可以将系统弃风功率限制在400 kW 内,风电消纳情况大大改善。

4.3.4 求解时间

本文在配置为AMD Ryzen 5 4600H CPU @3.00 GHz 和Nvidia GeForce GTX 1650 4 GB 的 计算机上进行仿真,在MATLAB R2020b 平台上利用YALMIP 工具箱配合CPLEX 求解器对MINLP 模型进行求解。在此平台上,针对含300 辆电动汽车的EVPP,单次日前优化平均求解时间为786.25 s,单次日内MPC 滚动优化平均求解时间仅为2.46 s。由于本文方法基于MPC 理论,日内优化窗口长度缩短,滚动优化1 次所需时间也大幅减少,降低了优化的粒度,提高了优化的效率。针对所设定的15 min调度时段,本文调度方法能有效、实时地在调度时段内下达调度指令并对电动汽车充放电进行控制。

5 结语

本文研究了考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度方法。针对当下日前风电和基础负荷预测精准度不够、EVPP 实时调度较少更新预测信息等问题,提出了CEEMDANBiLSTM 风电和基础负荷预测模型和含EVPP 的区域电网多时间尺度调度模型。通过算例验证,可以得到以下结论:

1）本文所提的CEEMDAN-BiLSTM 风电和基础负荷预测方法,能有效地提取数据不同时间尺度下的特征,提高神经网络学习效率,从而进行精准预测,同时,又具有普适性,可以推广至多种波动性大的数据时序预测场景。

2）本文所提出的区域电网多时间尺度调度模型,在CEEMDAN-BiLSTM 预测模型的基础上,通过日前-日内多时间尺度优化,能够进一步改善新能源电力系统负荷波动的效果,平抑日前风电预测误差,提高新能源系统运行稳定性,可以推广至新能源快速增长的电网以进行协同调度。

3）本文所提的模型也有需要改进的地方。当EVPP 容量进一步增大,电动汽车数量增加时,其求解时间也会成比例的增加,当出现海量电动汽车参与电网调度时,需要找到一种加快求解速度的方法,以应对EVPP 规模不断增长的趋势。本文下一步研究内容是在EVPP 满足风电消纳要求的情况下,优化海量电动汽车充放电功率,并且将功率分解到每辆电动汽车,以满足实际调度的需要。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。