基于代理模型进化算法的用户侧灵活爬坡产品交易策略

龚 开，黄鹏飞，王 旭，蒋传文，吕 冉，郭明星

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学）,上海市 200240；2. 华为技术有限公司,广东省深圳市 518000；3. 国网上海市电力公司,上海市 200135）

0 引言

随着“碳达峰·碳中和”计划的开展,预计2030 年中国风电、太阳能等清洁能源发电总装机容量将达到1.2 TW 以上［1］。高比例清洁能源并网引起的出力随机性和波动性势必会给电力系统带来更大的调节压力,电力系统调度灵活性亟待提升。

在提升电力系统灵活性方面,技术手段［2-6］固然重要,市场产品的辅助推动也尤为关键。在需求侧参与电力市场的研究中,综合能源系统［7］、需求响应［8］、虚拟电厂［9-11］可以参与调频等辅助服务,为电力系统有功平衡提供调节资源。然而,仅依靠调频等辅助服务还不足以应对大规模新能源并网带来的波动性和不确定性,频繁地调用调频服务会加剧系统调频负担,且会增加区域控制偏差［12］。为应对净负荷的大幅波动,系统需要有足够的灵活爬坡能力,因此,美国两大区域输电机构——加州独立系统运营商（CAISO）和中部大陆独立系统运营商（MISO）设计了灵活爬坡产品（flexible ramping product,FRP）以应对系统可能出现的爬坡容量缺额［13］。目前,FRP 的研究主要集中在系统层面的灵活爬坡备用调用方法［14-15］和风光、电动汽车提供FRP 可行性分析及建模［16-18］方面,而针对需求侧及其聚合体的FRP 交易策略的研究较少。文献［19］利用可中断负荷机制对用户侧提供FRP 进行了研究,但是其过程需要引导用户披露私有信息与参数,随着用户对私有信息逐渐重视,所提方法在实际应用中存在一定的难度。

需求侧聚合体模式主要有虚拟电厂、微网、主动配电网和负荷聚集商等［20］。其中,虚拟电厂能够不受地理位置限制,灵活聚合各类资源,提供各类电力产品,在用户侧资源管理和调度方面具有较强的优势［21］。文献［22-24］讨论了虚拟电厂在管理需求侧可调负荷的同时实现最大化市场收益的最优调度问题。在虚拟电厂对内部资源定价的问题上,文献［25］基于主从博弈制定了虚拟电厂与聚合体内电动汽车的售电价格；文献［26］提出了考虑虚拟电厂多类电力产品的配电侧市场出清模型,并基于数学解析模型推导了相应的定价方法。然而,以上文献并未考虑主体隐私问题,在实际应用场景中,由于隐私信息的获取难度大,难以构建直观的数学解析模型,从而无法采用常规数学推导进行求解。文献［27］考虑了虚拟电厂的隐私,基于Kriging 模型构建了配电网运营商与多虚拟电厂主从博弈下的定价和能量管理模型。然而,Kriging 模型采用的是高斯过程（Gaussian process,GP）回归模型,计算复杂度较高,且单一模型无法全面提取数据的各项特征,适用范围受到一定限制。

综上,本文提出一种基于随机排序的代理模型进化算法（surrogate-assisted evolutionary algorithm,SAEA）的用户侧虚拟电厂（demand-side virtual power plant,DS-VPP）FRP 交易策略。该策略基于用户公开信息,实现了DS-VPP 对用户侧FRP 的管理和调度。主要贡献如下:

1）构建了DS-VPP 能源交互双层优化模型,主要考虑了DS-VPP 为不同类型用户提供能源、收购FRP 等商业行为,明确了用户与虚拟电厂在FRP 市场中的定位。

2）针对用户隐私信息获取困难导致常规数学解析算法难以实际应用的问题,提出了一种基于随机排序的SAEA 求解所提双层优化问题。该算法避免了直接采集用户隐私数据,且采用随机排序方法减少了单一模型造成的误差,实现了较为精确的求解。

1 DS-VPP 能源交互双层优化模型

1.1 模型介绍

本节主要介绍DS-VPP 对外提供各类电力产品、对内向用户购买/出售各类电力服务的数学模型。一般而言,DS-VPP 主要聚合了4 种电力资源,即不可控电源、可控电源、不可控负荷和可控负荷,具体负荷类型如附录A 图A1 所示。DS-VPP 在管理上述电力资源时,需要满足内部用电负荷需求,在市场中买卖缺额电量/富裕电量。用户如果有意愿提供FRP,也可以和DS-VPP 签订合同,由DS-VPP购买后作为代理,统一参与到FRP 交易市场中。

DS-VPP 能源交互优化模型是一个双层优化模型。上层优化模型为DS-VPP 作为用户侧各类电力资源代理商参与电力市场,以最大化自身收益为目标购买/出售各类电力商品,决策变量为与内部各用户签订的电力商品价格；下层优化模型为用户以最小成本向DS-VPP 购电,有意愿提供调节向上/向下FRP 的用户也可以与DS-VPP 签订合约,决策变量为电力需求量和FRP 提供量。考虑到FRP 交易时间尺度一般为15 min,而主能量和批发市场交易时间尺度一般为1 h,为方便联合优化,所提模型的优化时间尺度定为15 min。具体数学模型如式（1）至式（9）所示。

式（5）为用户购电成本最小目标函数,主要分为6 项:第1 项 为 用 户 向DS-VPP 购 电 成 本；第2 项 为用户向其他售电商签订的购电成本；第3、4 项分别为用户提供向上、向下FRP 的收益；第5 项为用户提供向上FRP 的成本［28］；第6 项为用户增加用电提供向下FRP 的成本。

式（6）表示总的用户申报用电量包括不可控负荷用电量Pucl和可控负荷用电量Pcl。式（7）和式（8）表示可控负荷申报用电量Pcl与申报灵活爬坡产品Pru和Prd应在运行限制范围内。FRP 不仅包括提供的爬坡功率,也包括其对应的爬坡率。kru和krd定义为在时刻t+Δt和t间隔中,DS-VPP 负荷曲线的变化速率。结合附录A 图A2,以向上FRP 为例,DSVPP 从时刻t的用电需求Pcl降至时刻t+Δt的Pcl-Pru,等同于以向上爬坡速率kru向电网提供了Pru的向上灵活爬坡产品。

式（9）表示不可控负荷用电量Pucl申报范围。一般而言,不可控负荷不存在自主调整空间,但用户可以根据用电习惯或电价差异自由选择其他售电商。因此,不可控负荷总用电量固定,而从DS-VPP购买的电量存在一定变化范围。

1.2 考虑预测不确定性的优化模型

在模型式（1）至式（9）的常数项中,大部分是经过预测获得的数据,例如风电出力Pwd,用户用电可控和不可控负荷上下限Pcl,max、Pcl,min和Pucl,max、Pucl,min等。由于预测技术精确性的限制,上述预测数据值与实际值存在一定的误差,此类误差可以称为预测误差,或者预测不确定性。预测误差导致了系统爬滑坡能力的概率性不足,FRP 为电网调度中心提供了额外的备用资源。在1.1 节讨论的DS-VPP 能源交互模型中引入预测不确定性,模型转化如下:

2 基于随机排序的SAEA

2.1 算法流程介绍

智能优化算法的提出已有多年,其在多种领域的应用已十分成熟。在算法流程中,适应度函数的评价决定了算法的搜索方向,然而现实中,很多优化问题的适应度函数难以建模,这一问题限制了智能算法的应用范围。为解决该问题,代理模型技术受到关注并有机地和智能优化算法融合,形成了SAEA［32］。由于代理模型大多基于已有的历史数据构建模型,故也可以称为数据驱动进化算法（datadriven evolutionary algorithm,DDEA）。

由于数据信息获取有限,SAEA 领域的研究大多集中在如何利用有限数据量来构建精确的代理模型,例如多项式回归［33］、人工神经网络［34-36］、径向基函数网络（radial basis function network,RBFN）［37-39］等。在前馈神经网络研究中,基于插值法的RBFN在决策变量数量较多时具有计算成本较少、训练速度快［40］等特点,从而得到广泛的应用。RBFN 主要包括输入层、隐藏层和输出层,如图1 所示。

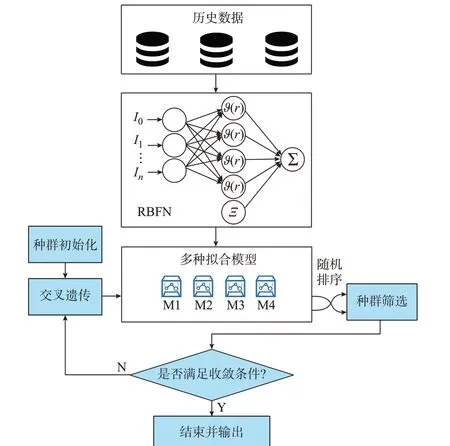
图1 基于随机排序的SAEA 结构Fig.1 Structure of stochastic ranking based SAEA

其中,隐藏层的第i个神经元ϑi(r)使用径向基函数作为核函数,采用输入Ii与中心点ci的欧氏距离r为函数的独立变量,如式（14）所示,中心点可以通过K-means 聚类算法获得。RBFN 与传统三层神经网络最大的区别在于隐藏层使用径向基函数作为激活函数,该函数的取值仅与到中心点的距离有关。

式中:σ为扩展常数,控制着每个神经元代表的中心点的影响范围,其值越大表示每个中心点影响的范围越大。

不同的核函数可以提取数据信息的不同特征,为了高效地利用有限的数据信息,可以基于不同的核函数构造出不同的RBFN,并通过随机排序的方式组合这些RBFN,从而形成基于随机排序的数据驱动进化算法（SRK-DDEA）［41］。如图1 所示,基于式（16）至式（19）构造的4 种不同的RBFN 形成了M1、M2、M3、M4 这4 种代理模型。由于不同的拟合模型产生的误差不同,采用平均值方法得到代理模型的适应度评价是不合理的。随机排序方法原本用于多目标优化问题中平衡优化目标与约束［42］,在本文所提算法中可以利用随机排序方法平衡多个代理模型,从而避免单一代理模型误差过大而导致的寻优偏离。基于以上思路,DS-VPP 动态定价决策算法筛选最优种群的过程如表1 所示。

表1 基于SRK-DDEA 的动态定价算法流程Table 1 Process of dynamic pricing algorithm based on SRK-DDEA

在每个迭代轮次中,父代P交叉遗传生成子代Q后,将所有个体代入4 种拟合模型,获得对应的适应度函数,随后通过随机排序法对种群进行排序。针对代理模型的构建过程,附录A 图A4 介绍了代理模型的输入、输出数据来源,将虚拟电厂与用户签订的售电价格和向上/向下FRP 收购价格作为构建代理模型的输入数据,将虚拟电厂在当前价格决策下的购售电收益作为构建代理模型的输出数据,输入和输出数据之间的函数关系利用RBFN 形成代理模型。

2.2 针对所提算法的讨论

根据表1 可以看出,SRK-DDEA 实际上不依靠1.1 节中数学解析模型求解,而直接利用输入、输出数据形成代理模型,对代理模型进行寻优获得最优解。因此,1.1 节中数学解析模型构建的意义在于:1）生成足够的输入、输出数据；2）通过KKT 条件求解获得理论最优解,形成可以与所提算法对比的对照案例,以验证所提算法的正确性和准确性。因此,在第3 章算例分析中,每一个具有对照组的算例都是分别按照SRK-DDEA 和KKT 分析2 种方法获得的算例。

3 算例分析

3.1 算例设计说明

本文所提模型中涉及的现货市场出清电价、零售市场电价、风电出力、可调节用户最大容量等信息如附录A 图A5 所示,数据来源于PJM 2020 年市场信息［43］。本文常量系数设置信息如下:δmcd和δmcu均设 为0；θwill设 为1；αdis中 元 素 设 为0.22 美 元/MW；Aru中 元 素 设 为0.005 美 元/MW2；bru中 元 素 设 为0.013 美 元/MW；λes中 元 素 设 为0.005 美 元/MW2；Rru和Rrd中元素均设为最大调节容量20 MW/min。此算例假设仅包含一个大的用户主体,所有用户设备均在该主体内,因此向量中只有一个元素。

在算法精确性验证方面,本文采用数学理论推导辅佐算法验证的方式,通过对所提模型进行KKT分析优化求解问题,然后将求解结果与本文所提方法计算结果进行对比分析,从而验证所提方法的精确性。KKT 分析的相关数学推导公式见附录B。

3.2 仿真结果分析

本节算例分析分为5 个部分:第1 部分为算例收敛性与精确性验证,针对考虑不确定性因素的优化模型进行算例分析；后4 个部分为计算成本、方法对比与价格影响等案例分析,由于算法精确性已在第1 部分进行验证,后续算例分析均不考虑不确定性因素的影响。

3.2.1 可行性和精确性验证

基于1.2 节所提考虑不确定性的优化模型,需要明确风电出力预测不确定性场景和负荷预测不确定性场景的数量。首先,采用MATLAB 内置预测模块进行预测并获取预测误差,以此作为算例中可能出现的不确定性场景,如附录A 图A6 和图A7 所示。通过K-means 聚类后,风电出力预测不确定性场景和负荷用电不确定性场景缩减为5 类,并剔除低概率场景,获得3 类风电出力预测不确定性场景[-268.76,79.96,578.65] 及 其 对 应 概 率[0.297,0.557,0.146]和2 类用电负荷预测不确定性场 景 [5.40,-1 636.56] 及 其 对 应 概 率[0.953,0.047]。

随后,基于附录A 图A5 中前18 个时刻数据,采用拉丁超立方采样生成4 000 组决策变量数据并输入1.2 节所提模型,获得与之对应的目标函数值,从而形成4 000 组输入、输出数据集。将数据集导入SRK-DDEA,获得最优解如附录A 图A8 至图A11所示,每个时刻重复10 次计算。图中的误差线包含上误差线和下误差线,上误差线为最大值与中位数之差,下误差线为中位数与最小值之差。根据测算,SRK-DDEA 与KKT 算法收益结果的平均误差为0.022 9%,而售电价格、向下FRP 价格和向上FRP价格的平均误差分别为1.79×10-9%、0.079 3%和0.081 1%,以上误差在虚拟电厂的日常运行中是可接受的。因此,测试结果证明了SRK-DDEA 在DSVPP 对FRP 最优交易决策中的可行性与精确性。

3.2.2 不同数量代理模型的影响

为验证多种代理模型能够提高拟合模型的精确性,本节选择如下4 种具有代表性的场景,所有场景均在t=1 时刻下模拟:

1）采用1 种代理模型的SRK-DDEA（1k）,核函数为Gaussian 函数；

2）采用2 种代理模型的SRK-DDEA（2k）,核函数为1k 的核函数加上Reflected 函数；

3）采用3 种代理模型的SRK-DDEA（3k）,核函数为2k 的核函数加上Multiquadric 函数；

4）采用4 种代理模型的SRK-DDEA（4k）,核函数为3k 的核函数加上inverse multiquadric 函数。

测试结果如图2 所示,可以发现1k 和2k 案例过早收敛,而采用了4 种核函数的4k 案例结果更接近于理论收益最优值6 316.273 美元,尤其是4k 和1k案例对比,4k 案例的结果远好于1k 案例,正是由于不同核函数可以提取数据的不同特征,并借助随机排序避免寻优偏离,更好地实现拟合。观察2k 和3k案例可以发现,算法求解结果差异不大,可能是由于采样数据不均匀造成。总的来说,包含多个核函数的SRK-DDEA 可以更为有效地求解虚拟电厂在用户信息获取受限情况下的优化问题。另一方面,多个代理模型会导致计算成本上升,在实际应用中需要平衡计算精度和时间成本,合理选择代理模型的数量。

图2 不同代理模型数量下SRK-DDEA 拟合结果对比Fig.2 Comparison of SRK-DDEA fitting results with different number of surrogate models

3.2.3 计算成本比较分析

GP 与RBFN 类似,都可以实现输入与输出关系的拟合过程。本节将对比GP 和RBFN 的计算成本,测试结果如图3（a）和（b）所示。

图3（a）中测试时段表示优化过程中考虑的时段,例如2 个测试时段表示需要同时优化2 个连续时刻的决策变量。从图中可以发现,在数量较少的测试时段案例中,GP 相较RBFN 具有较好的优势,说明GP 在低决策变量环境下计算成本较低,而随着测试时段的增加,决策变量逐步增多,GP 所需计算时间显著增加且超过RBFN 的计算时间。观察图3（b）可以发现,随着测试时段的增加,GP 拟合的模型也逐渐偏离理论最优点,RBFN 则保持了较为良好的拟合效果。

3.2.4 平均值与随机排序方法比较分析

随机排序法可以避免单一代理模型误差过大而导致的寻优偏离。本节为验证该说法,采用随机排序法和平均值法2 种方法进行仿真拟合,对比2 种方法的计算时间和计算精确性,结果如图3（c）和（d）所示。从图3（c）可以看出,随机排序法相较于平均值法,更加贴合KKT 理论值曲线。具体而言,平均值法在8 个时段的平均误差为1.898%,随机排序法则为0.099%。在计算时间上,从图3（d）可以看出,2 种方法的计算时间不分伯仲。具体而言,平均值法在8 个时段的平均计算时间为83.006 s,随机排序法的平均计算时间为81.451 s。通过该算法可以发现,随机排序法在与平均值法类似的计算时间下,可以实现更优的精确度。

3.2.5 DS-VPP 价格影响因素分析

首先,对不可调节用户的用电习惯进行差异化设置,测试不同场景下DS-VPP 交易决策的不同。2 种场景描述如下:

场景1:在该场景下,不可调节用户与DS-VPP签订购电量最低值满足Pucl,min=Pucl,max/2,即不可调节用户的用电量无论DS-VPP 售电价格如何变化,均会有部分电量与DS-VPP 签订。

场景2:在该场景下,不可调节用户与DS-VPP签订购电量最低值满足Pucl.min=0,即不可调节用户的用电量完全受DS-VPP 售电价格影响,拥有完全的选择不同售电商的权利。

测试结果如附录A 图A12 和图A13 所示。可以看出,在场景1 中,DS-VPP 售电价格的制定完全与零售价格（见图A5）重合,即用户售电商自主选择权一定程度受限时,与用户签订合约的DS-VPP 的售电定价不会受到其他厂商售电价格的影响。反观场景2,由于不可调节用户的全部用电量拥有自主选择售电商的权利,DS-VPP 会在高风电出力时刻降低售价,与其他厂商竞争电量,以获得更多的售电收益。

然后,对2 种FRP 价格机制进行测试。2 种不同的FRP 价格机制设置如下:

场景3:FRP 价格上限与时间相关,从而反映不同时刻下FRP 的实际价值,如附录A 图A5 的FRP价格上限曲线所示。

场景4:FRP 价格上限为固定值,设置为场景3的FRP 价格上限的中位数0.230 4 美元/MW。

如图4 和图5 所示,对比分析场景3 和场景4 可以发现,场景3 中用户提供的FRP 容量更大,爬坡率也更高,平均爬坡率达1.07 MW/min,平均滑坡率达1.04 MW/min,而场景4 中平均爬坡率为1.04 MW/min,平均滑坡率为1.03 MW/min。其原因在于,相比场景4,场景3 中DS-VPP 在某些时刻为用户提供的价格更高,用户愿意提供更多FRP。从调节难易角度来看,由于场景4 的FRP 价格固定,用户在不同时刻提供的FRP 容量的差距不大,对用户的响应技术要求更低,比较适合FRP 市场的初期运行。随着FRP 市场的成熟,可以采用场景3,从而进一步挖掘用户侧的调节潜力。

图4 场景3 下DS-VPP 的FRP 定价与用户提供量Fig.4 FRP pricing and amount of DS-VPP provided by user in scenario 3

图5 场景4 下DS-VPP 的FRP 定价与用户提供量Fig.5 FRP pricing and amount of DS-VPP provided by user in scenario 4

4 结语

本文针对用户侧FRP 交易决策问题,提出了DS-VPP 能源交互双层优化模型,为用户侧FRP 的实施提供了可行思路。针对虚拟电厂在与用户交易过程中对交易产品的价格决策问题,提出了基于随机排序的SAEA 交易决策方法,该方法的优点在于以下3 个方面:

1）该方法利用采样数据拟合用户对不同电价水平的响应行为,实现了基于公开信息的用户建模,克服了实际管理过程中用户隐私数据难以获得的难题；

2）与传统KKT 方法作分析对比,所提算法的精确性和收敛性得到了验证,在PJM 电价数据集上的测试结果显示算法精确性可以满足工程需求；

3）通过该方法测试了不同种类FRP 的价格机制,发现固定价格机制适合FRP 市场建设初期,时序价格机制可进一步挖掘需求侧调节潜力,更适合FRP 市场成熟期。

DS-VPP 对FRP 的交易策略还受到用户加入与退出虚拟电厂行为的影响。本文并未探讨虚拟电厂在管理过程中各主体自由进入和退出的行为,在后续的研究中会进一步探讨虚拟电厂动态聚合各类资源的技术与方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。