基于多场景置信间隙决策的风光储联合鲁棒规划

彭春华，熊志盛，张 艺，孙惠娟

（华东交通大学电气与自动化工程学院,江西省南昌市 330013）

0 引言

在当前节能减排和能源可持续发展的时代背景下,以风电和光伏为代表的大量分布式可再生能源（distributed renewable energy,DRE）接入电网得到了迅速发展［1］。然而,可再生能源出力易受自然环境影响而具有明显的波动性和不确定性,会对电网的稳定运行造成较大影响,这严重制约了电网对可再生能源的消纳。通过风光储联合规划有利于实现风光储多能互补,对于提高可再生能源消纳、减少系统投资成本具有重要价值。

鉴于风电、光伏出力具有间歇性、波动性和随机性,风光储联合规划属于典型的不确定性规划问题,针对此类不确定性规划的处理方法主要有鲁棒优化（robust optimization,RO）和 随 机 规 划（stochastic programming,SP）［2］。然而,现有RO 和随机规划方法均有所不足［3］:RO 研究中鲁棒性的设定往往偏于保守,且通常采用预设的不确定集合刻画多重不确定性,难以体现各类随机因素实际具有的多态性（如风光出力的分布特征具有季节差异性和不对称性）,导致鲁棒评价过于粗略而且难以反映真实的鲁棒度；而随机规划则通过场景缩减,将以区间域表示的不确定集合简化为若干典型场景进行多场景确定性优化,易丧失区间遍历性而难以保证规划的鲁棒性。为克服RO 过于保守而随机规划鲁棒性不足的弊端,分布鲁棒优化（distributionally robust optimization,DRO）研究不确定参数在最恶劣概率分布下的优化结果,兼顾鲁棒性与经济性［4］,在储能规划领域得到了不少应用。如文献［5］采用基于KL（Kullback-Leibler）散度的DRO 描述风电出力不确定性,建立了储能鲁棒机会约束规划模型；文献［6-7］将Wasserestein 距离分别作为风电、光伏概率分布模糊集的量度方法,建立了储能不确定性规划模型。文献［8］在储能最优配置中,利用二阶矩信息描述风电功率预测误差概率分布集。DRO 可使规划方案在经济性与保守性之间取得一定平衡,但从其要求确保最恶劣模糊场景下优化解可行的角度来看,仍偏于保守且灵活性不足。

近年来,一些学者还引入信息间隙决策理论（information gap decision theory,IGDT）处理含可再生能源的电力系统运行规划问题。基于风险规避的IGDT 并不追求满足极端场景,而是让优化结果在满足预设值的前提下,寻求不确定变量允许的最大波动范围［9］。然而,IGDT 在描述不确定集合方面同样存在表达过于粗糙的弊端:采用对称盒式集描述不确定变量的最大波动区间,难以体现超长时空尺度下各类随机因素实际具有的多态性,以及鲁棒性与不确定区间上下限可能存在的非线性关系。

综上所述,鉴于现有RO、随机规划和IGDT 等不确定性规划方法存在诸多不足,本文拟将随机规划和RO 相结合,综合多场景聚类分析和分类概率区间估计细化构造置信不确定集合,从而将常规的多场景确定性规划泛化为分类场景集置信不确定区间规划。进一步融合IGDT 的鲁棒思想,提出多场景置信间隙决策理论（multi-scenario confidence gap decision theory,MCGDT）:在决策结果承担的决策风险概率尽量小的前提下,最大化不确定变量的置信不确定区间以最大化规避不确定性影响。MCGDT 以多维场景聚类细化构造海量不确定集合,以置信区间描述不确定变量的随机性与多态性,可实现更为准确而合理的不确定性规划。

为体现风光储联合规划在提高可再生能源消纳、减少系统投资成本方面的有效性,本文以风光消纳率和总投资成本为优化目标,构建基于MCGDT的风光储鲁棒规划模型。鉴于该模型包含不确定性机会约束和具有非凸非线性、高维不连续和多目标耦合等特点,求解难度很大。本文首先基于不确定性理论将模型中的机会约束进行等效确定性转换,并设计了一种新颖的交叉熵-雷达扫描微分进化（cross entropy-radar scanning differential evolution,CE-RSDE）算法以实现深度寻优和高效求解模型。

1 MCGDT 模型

含不确定变量优化问题的数学模型可描述为:

式中:f0为ζ等于其预测值ζ͂时（即确定性模型）求得的最优解；fa为引入不确定变量后预设的系统能容忍的最差目标值；θ为鲁棒系数,其值越大,说明对目标变差的容忍度越大；U(ζ͂,δ)为不确定变量波动区间,其中δ为不确定变量的波动系数,δ>0。

式（2）中的U(ζ͂,δ)越大,则鲁棒性越强。然而,模型中预设的目标值难以刻画其实际值偏离f0的显著性水平。采用对称波动区间U(ζ͂,δ)描述不确定集合过于粗糙,无法体现随机因素的分类概率特征。此外,当不确定变量的概率分布为非对称时,这种对称描述易与实际区间发生错位,难以准确反映实际不确定区间,如图1（a）所示（以渐变颜色区分不同δ下的U(ζ͂,δ)）。

图1 不确定变量的波动区间Fig.1 Fluctuation interval of uncertain variables

为解决上述问题,本文通过引入机会约束对不确定集合和目标偏差进行概率评价:取消不确定变量波动系数δ,以置信不确定区间代替IGDT 的对称波动区间；取消主观预设的鲁棒系数θ,引入机会约束,确保在决策结果所承担的决策风险概率尽可能小的条件下,最大化不确定变量的置信不确定区间,从而最大化规避不确定性的影响。由此,提出如下置信间隙决策理论（confidence gap decision theory,CGDT）模型:

为进一步精细化描述超长时空尺度下的海量场景,通过多维场景聚类将海量场景细化分解为复杂度和差异度较低的相近时空场景集；统计分析获取各场景集内风电、光伏出力和负荷需求分维概率分布以及由置信水平决定的分类置信不确定区间,从而将常规的多场景确定性建模拓展泛化为基于分类场景集的置信不确定区间建模,以精细化构造原不确定性集合。将分类多场景集置信不确定区间嵌入CGDT 模型,得到的MCGDT 模型如式（4）所示。

式中:N为场景集总数；ωs为场景集s的权重系数；含下标s的变量为式（3）中相应变量在场景集s中的分量,下同。

与IGDT 模型相比,MCGDT 模型采用基于场景聚类和概率评价的建模分析,可实现海量场景的精细量化和置信鲁棒度与系统综合目标的协同优化,合理而准确地反映优化结果的鲁棒性。同时,通过置信水平可更加真实地衡量非线性鲁棒度,灵活合理地描述不确定区间而不发生区间错位,如图1（b）所 示（以 渐 变 颜 色 区 分 不 同1-α下 的U(ζ͂,α)）。

2 不确定变量的分类置信不确定区间

风光储鲁棒规划属于大时空尺度下的长期优化问题,其不确定区间宽泛而复杂。为此,本文首先基于高效的增强k-means-+聚类算法［10］进行多维场景缩减,将大时空尺度海量场景细化分解成N个簇（亦即N个相近时空场景集）,再对各场景集内风电、光伏出力和负荷需求时空相关性及随机特征进行分析,则可显著降低不确定变量概率分布模型的复杂度和差异度。

由式（6）可计算出各场景集权重系数ωs:

式中:ks为场景集s包含的场景数；k为场景总数。

风电、光伏出力和负荷需求的多态性决定了其具有不同的概率分布特征,各时段风光荷实际值与预测值之间存在一定偏差。参考文献［11］分别选用威布尔分布、贝塔分布和正态分布拟合各场景集的风速、光伏出力和负荷需求,实现各场景集的分维概率建模以充分体现风电、光伏出力和负荷需求的多态性。

设置信水平为1-α,风速、光伏出力以及负荷需求的置信不确定区间如附录A 图A1 所示（图中v͂t为t时刻风速的预测值）。根据文献［11］求得风电出力、光伏出力以及负荷需求的置信区间表达式为:

3 基于MCGDT 的风光储联合鲁棒规划

3.1 优化目标

为体现风光储联合鲁棒规划在提高可再生能源消纳和减少总投资成本方面的有效性,本文以风光消纳率和总投资成本为优化目标,并考虑电压偏差改善率［12］、储能荷电状态和储能充放电次数［13］等约束条件,构建基于MCGDT 的风光储联合鲁棒规划模型。模型约束条件见附录B,目标函数如下。

1）风光消纳率最大化

分布式风电和光伏的输出功率具有间歇性和波动性,一定程度上限制了电网对风光的消纳［14］。为体现风光储联合规划的优越性,本文以风光消纳率作为优化目标之一,如式（10）所示。

式中:JC为总投资成本；JDG和JESS分别为可再生能源和储能系统的投资成本；JW和JS分别为风电机组和光伏电站的投资成本；r为贴现率；y为经济使用年限；CW、CS、CESS分别为风电、光伏和储能系统的单位容量投资成本；MW、MS、MESS分别为风电、光伏和储能系统的单位容量维护费用；CP,ESS为储能系统单位功率成本；EW,s、ES,s、EESS,s分别为场景集s中风电、光伏和储能系统的额定容量；PESS,s为储能系统额定功率。

3.2 基于MCGDT 的风光储联合鲁棒规划建模

设确定性模型得到的风光消纳率和总投资成本的最优解分别为f01和f02（其在场景集s中的分量分别为fs,01和fs,02）。根据MCGDT,将式（4）与式（10）、式（11）联立可转化为如下MCGDT 规划模型:求解,本文采用文献［15］提出的不确定性理论对其进行等价确定性转换,则该约束可转化为式（15）所示的等价确定性约束,具体推导过程见附录C。

4 求解算法

由于第3 章构建的基于MCGDT 的风光储联合鲁棒规划模型具有非凸非线性、高维不连续和多目标耦合等特点,求解难度很大,本文拟采用高效的多目标分子微分进化（multi-objective molecular differential evolution,MOMDE）算法对其进行求解。MOMDE 算法包括种群混合、非劣排序、种群更新等操作,具体流程可参见文献［16］。然而,在求解高度复杂的基于MCGDT 的风光储联合鲁棒规划模型时,常规MOMDE 极易导致进化后期种群失去个体多样性,使得进化趋于停滞,难以实现该模型的深度寻优与高效求解,得不到准确完整的帕累托前沿。究其根本原因,当进化后期接近最优解时进一步深入优化已属于小概率事件,进化难度会显著增大,同时也会加剧个体多样性的丧失,而个体多样性不足又会进一步导致进化停滞。为了提升算法在进化后期的深度寻优效率,同时提高寻优搜索的遍历性,本文提出在MOMDE 中引入交叉熵重要采样（cross entropy-importance sampling,CE-IS）原理与雷达扫描机制,设计出一种新颖的CE-RSDE 算法。

4.1 交叉熵重要采样原理

CE-IS 常用于处理小概率事件,其基本思想是在保持样本数学期望不变的条件下,通过求解2 个函数间的最小KL 距离来构造样本原概率密度函数的近似函数［17］。由于样本在该近似函数上的概率分布相较于原概率密度函数大得多,依此近似函数进行随机抽样便可将原问题转化为大概率事件估计问题,从而显著提高小概率事件的处理效率。

假设样本的概率密度函数为g*(x)且g*(x)属于函数族h(x；u)。通过求解未知数u以构造新的概率密度函数h(x)（h(x)也属于该函数族）,使得h(x)与原概率密度函数g*(x)的KL 距离最小,此距离的数学定义如下:

将上述可高效处理小概率事件的CE-IS 机制融入微分进化中:

1）优选个体构造小规模精英种群,提取精英种群的均值μ和方差σ2以构造概率密度函数；

2）基于精英种群概率分布随机生成大规模新种群；

3）经微分进化和非劣排序后抽取优势个体集更新精英种群；

4）更新精英种群的概率密度函数。

如此,通过不断循环更新即可使得精英种群的概率分布向最佳的概率密度函数逼近,从而实现进化后期个体抽样效率的显著提升。

4.2 雷达扫描机制

现代雷达技术为了实现全局扫描和精准定位,其波束在目标可能出现的范围内进行周期性系统扫描。从附录A 图A2 可以看出,越靠近天线中轴线位置,电磁波辐射场强越大,搜索强度越强,而远离其中轴线的位置,辐射场强呈振荡衰减,对应的函数表达可用抽样信号函数（即Sa 函数）表示［18］:

在求解高度复杂的MCGDT 规划模型时,随着进化后期个体多样性下降,式（18）中的变异差分项Xr1,g-Xr2,g会过早趋于零而导致变异停滞陷入早熟。为此,受雷达扫描机制的启发,通过在变异差分项叠加振荡幅值可随迭代次数自适应增强的Sa 函数,构造如式（19）所示的雷达扫描变异机制。

式中:λ为逻辑值；g为当前迭代次数；gmax为最大迭代 次 数；rand（1,m）表 示 产 生m个0～1 之 间 的 随机数。

如附录A 图A3 所示,雷达扫描变异机制不仅可连续周期性振荡遍历扫描变异参数与变异差分项,且扫描强度可随迭代次数的增加而自适应增强,能有效防止进化后期因扫描强度不足而陷入早熟。因此,CE-RSDE 算法可显著提高算法持续遍历寻优能力,实现对基于MCGDT 的风光储联合鲁棒规划模型的深度寻优。

本文提出的用于求解基于MCGDT 的风光储联合鲁棒规划模型的CE-RSDE 算法流程见附录A图A4。

5 算例分析

5.1 算例概况

本 文 选 择IEEE 33 节 点 系 统［19］在MATLAB R2014b 编译环境下对所提理论进行风光储联合规划验证,其网络结构见附录A 图A5。假设从节点2到节点33 都允许配置风光储设备,其中风电、光伏各可配置2 处位置,储能系统配置位置和数量不限（通过优化计算确定）。设风电机组的投资成本为0.4 万元/kW,年维护费用为20 元/（kW·a）；储蓄电池的充、放电效率均为0.92,荷电状态上、下限分别为0.8 和0.2,其余经济参数参考文献［20-21］；规划中的光伏单组容量为100 kW,风电单台容量为500 kW,储蓄电池单组规格为2 V/1 000 Ah。根据项目需要,电压偏差改善率下限设为1.4,储能系统日充放电次数上限为4；多维聚类场景集数为5 个,CE-RSDE 算法的种群规模为100,最大迭代次数为1 500,精英种群比例为0.4,交叉概率因子为0.6,变异尺度因子为0.3。计算机配置为AMD Ryzen5 3550H 3.7 GHz CPU,16 GB 内存。

为模拟各类负荷需求的特殊性,本文设定节点1 至10 为 商 业 负 荷,节 点11 至25 为 居 民 负 荷,节 点26 至33 为工业负荷。统计某地全年风速、光伏功率和分类负荷数据,并将其作归一化处理以便后续计算。

5.2 结果分析

5.2.1 不同目标显著性水平对比分析

优化求解确定性模型得到的最优解DR=76.12%和JC=2.41×107元。为验证决策方案所承担的决策风险概率对规划结果的影响,分别将目标显 著 性 水 平β的 值0.05、0.10、0.15 和0.20 代 入MCGDT 模型中,优化求解得到不同β下的帕累托前沿对比如图2 所示。

图2 不同目标显著性水平下的帕累托前沿Fig.2 Pareto frontiers at different significance levels

由图2 可知,风光消纳率与总投资成本呈相互制约的非线性关系,若想达到更高的风光消纳就需投入更多成本,反之亦然。此外,曲线斜率随着风光消纳率的增加而逐渐增大,意味着当可再生能源消纳达到一定程度时,需要额外投入更多的资金才能使之继续获得微小提升,性价比很低,决策者在选择规划方案时应当注意（最佳折中解的位置也证明了此结论）。结合式（13）还能看出,目标显著性水平越小,风光消纳率和总投资成本优于预期目标的概率越大,相应的帕累托前沿会位于更下方。不同显著性水平对应的最佳折中解如表1 所示,具体方案详见附录D 表D1。

表1 不同显著性水平下的最佳折中解Table 1 Optimal compromise solutions at different significant levels

从表1 可以看出,β越大,即决策结果所承担的决策风险概率越大的情况下,风光消纳率和总投资成本劣于预期目标的概率越大,使得规划方案的实施效果越差,但对应的置信鲁棒度也会更大,即系统对环境变化有更好的适应能力。因此,决策者可根据自身的风险承受能力合理设置β值,使系统在应对不同比例的不确定变量时仍具有最佳的鲁棒性和最优的综合目标,由此证明了理论分析的正确性与可行性。

5.2.2 不同规划方法对比分析

为验证MCGDT 处理不确定性规划问题的优越性,本文将基于MCGDT 的风光储联合鲁棒规划的优化结果与基于IGDT、多场景法、CGDT、RO 和DRO 的风光储联合鲁棒规划的优化结果作对比。采用控制变量法,将不确定性处理方法视为实验变量,其余条件均一致,即统一采用CE-RSDE 算法优化求解模型,运行环境、算法及算例参数设置均相同。其中,MCGDT 和CGDT 的目标显著性水平取0.05,IGDT 的鲁棒系数取0.05,多场景处理方法见文献［22］,RO 采用盒式不确定集,DRO 基于矩信息构建模糊集［23］。不同方法所得最佳折中解如表2 所示,详细方案见附录D 表D2。

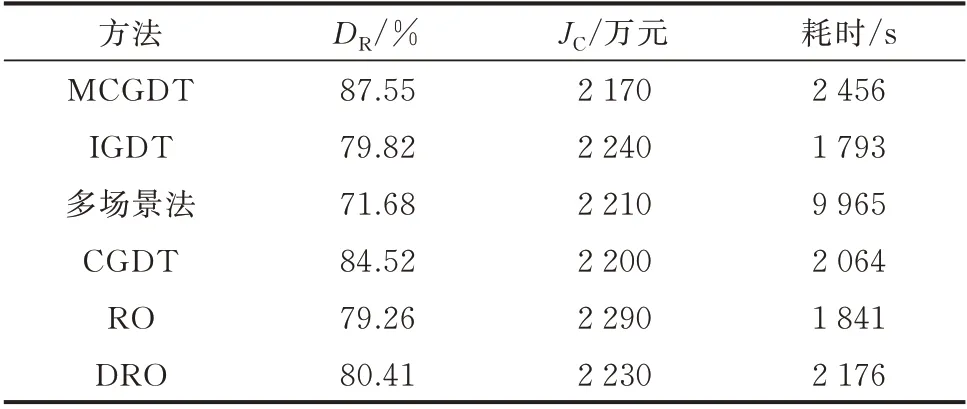
表2 不同方法下最佳折中解Table 2 Optimal compromise solutions with different methods

此外,为进一步验证各种方法对环境变化的适应性,评估电网应对风光荷不确定性影响的鲁棒性,本文采用蒙特卡洛模拟随机生成1 000 组风光荷场景,统计分析上述4 种方法所得方案的风光消纳率,由统计数据绘制的小提琴图如图3 所示。

1）MCGDT 与IGDT 比较

由表2 可知,由于MCGDT 考虑了基于场景聚类和概率评价的建模分析,因而耗时长于IGDT,但风光消纳率和总投资成本均更优（MCGDT 相比于IGDT,风光消纳率高7.73%,总投资成本少70 万元）。此外,从图3 可以看出,在随机生成的1 000 组风光荷场景下,MCGDT 风光消纳率小提琴图位置高于IGDT,其中位数高4.6%,而总投资成本小提琴图位置较低,其中位数少1.2×106元。这是因为后者鲁棒系数的设定过于主观且对不确定变量的描述过于保守和粗糙,在应对复杂多变的环境时电网鲁棒性较差。综上,MCGDT 较IGDT 具有更佳的鲁棒性和更优的系统综合目标。

图3 风光消纳率和总投资成本蒙特卡洛统计结果Fig.3 Monte Carlo statistical results of wind/photovoltaic power consumption rate and total investment cost

2）MCGDT 与多场景法比较

多场景法需要通过聚类算法将海量场景缩减为若干典型场景进行确定性规划,其耗时为9 965 s（如表2 所示）,约为MCGDT 的405.74%。值得注意的是,多场景法对应的总投资成本较少,这是因为该方法无法保证系统的鲁棒性,所得优化结果在某些特定场景下可能会获得较好的效果。然而,由2 种方法所得方案在1 000 组风光荷场景下统计分析可知（见图3）,MCGDT 风光消纳率小提琴图位置更高,其中位数高7.3%,而多场景法的位置最低；总投资成本方面,多场景法同样表现更差,且数据分布范围最大,可见多场景法难以保证不确定影响下系统的鲁棒性。因此,决策者若选用多场景法所得方案将会导致综合目标更差。综上,MCGDT 较多场景法具有更高的计算效率和更精确的优化结果,对环境变化有着更强的鲁棒性。

3）MCGDT 与CGDT 比较

由表2 可知,CGDT 未考虑超长时间尺度下随机因素的多态性,没有进行多维场景聚类,因而耗时少于MCGDT,但其总投资成本多30 万元、风光消纳率低3.03%。此外,从图3 可以看出,CGDT 风光消纳率小提琴图位置略低于MCGDT,其中位数低2.9%,而总投资成本中位数略高40 万元。由于MCGDT 将海量场景聚类后再进行概率评价,对不确定变量的描述更加精细,因而所得规划方案具有更优的鲁棒性和系统综合目标。综上,MCGDT 较CGDT 在消纳更多可再生能源的情况下具有更好的经济性,可促进分布式能源的最优利用。

4）MCGDT 与RO/DRO 比较

由表2 中的最佳折中解对比可知,RO 结果对应的总投资成本为2 290 万元,风光消纳率为79.26%,与MCGDT 结果相比差距明显；而DRO 结果对应的总投资成本为2 230 万元,风光消纳率为80.41%,均要好于RO,但整体比MCGDT 差。这是因为RO方法考虑最恶劣场景下的规划方案,需要投入大量不必要的资源来确保系统鲁棒性,因此所得优化结果具有很强的保守性；而DRO 方法改进了传统RO方法的不足,兼顾鲁棒性与经济性,因此所得规划方案各项指标都有所改善,但由于此类DRO 仅仅利用了不确定变量有限数据的矩信息来确保最恶劣“模糊场景”下的可行优化解,仍具有一定的保守性,因而效果差于MCGDT。从图3 可以看出,在1 000 组风光荷场景下,RO 和DRO 对应的风光消纳率中位数分别为69.4%和70.2%,总投资成本中位数分别为2 460 万元和2 370 万元,均劣于MCGDT 所得结果,但二者小提琴图分布范围较多场景法小,说明2 种方法对风光荷不确定扰动具有鲁棒性,可应对复杂多变的环境。综上,MCGDT 较RO/DRO 均具有更佳的鲁棒性和优化目标值,说明所提方法可充分挖掘规划方案对不确定性的承受能力,在不确定性处理方面更具优越性。

5.2.3 不同优化算法对比分析

为验证CE-RSDE 算法的优越性,客观评估算法的性能与求解效率,本文分别采用3 种优化算法:CE-RSDE、MOMDE 和NSGA- Ⅱ［24］求 解 基 于MCGDT 的风光储联合鲁棒规划模型。3 种算法参数设置均相同,即种群规模100,目标显著性水平0.05,最大迭代次数1 500。优化所得帕累托前沿如图4 所示,对应最佳折中解收敛过程如图5 所示。

由图4 可知,和其他算法相比,在迭代次数相同的情况下,CE-RSDE 算法可收敛到更准确的帕累托前沿,且所得帕累托前沿中的帕累托最优解分布更加广泛而均匀。如图5 所示,相同时间内,CERSDE 具有更快的收敛速度和更佳的深度寻优能力,能在进化后期持续遍历搜索全局最优解；而由于进化后期种群多样性的丧失,MOMDE 和NSGA-Ⅱ因早熟而陷入了局部最优。 综上可见,与MOMDE、NSGA-Ⅱ等其他算法相比,本文提出的CE-RSDE 算法能够实现深度寻优和高效求解模型,具有较为明显的优越性。

图4 不同算法的帕累托前沿Fig.4 Pareto frontiers of different algorithms

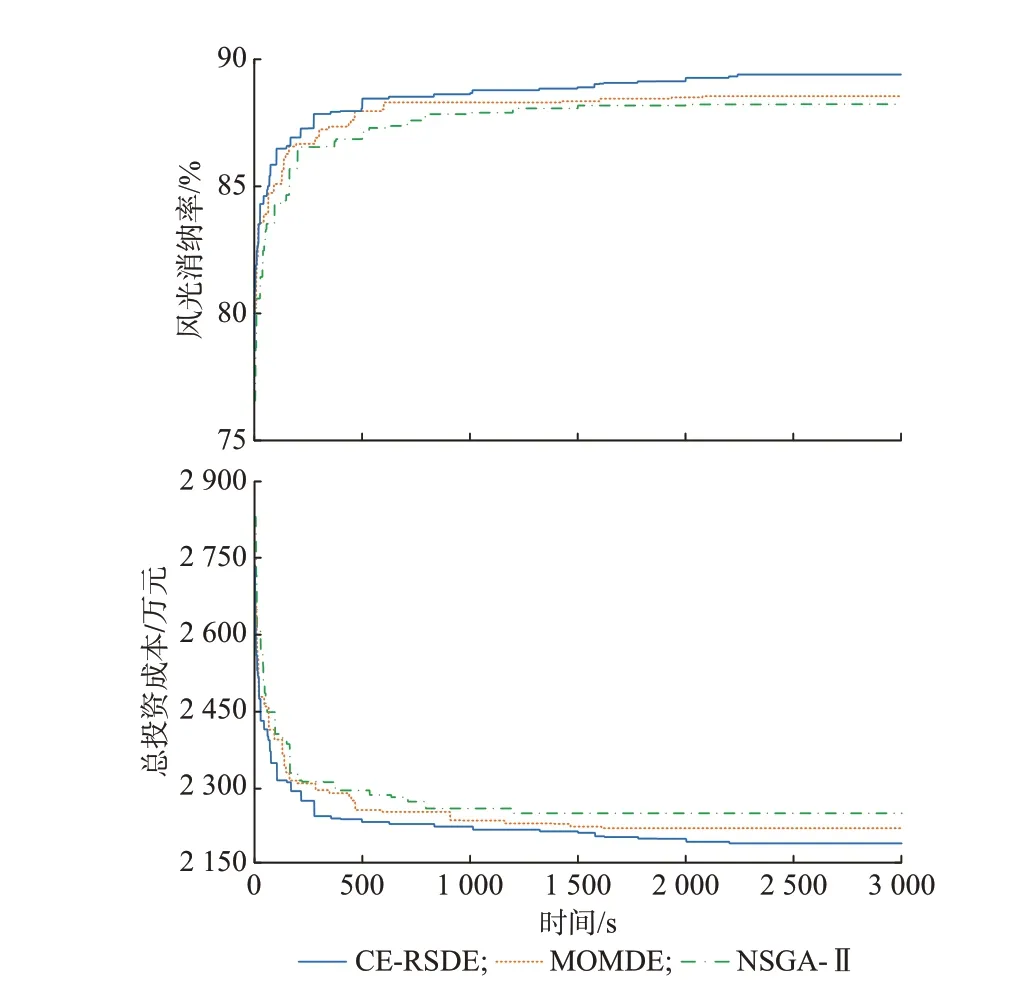
图5 不同算法的收敛过程Fig.5 Convergence process of different algorithms

6 结语

本文提出了基于鲁棒驱动的MCGDT,以风光消纳率和总投资成本为优化目标,建立了基于MCGDT 的风光储联合鲁棒规划模型,并融合CEIS 原理、雷达扫描机制和多目标微分进化,提出了CE-RSDE 优化算法求解模型。所提理论和算法具有如下优点:

1）MCGDT 实现了海量场景的精细量化、置信鲁棒度与系统综合目标的协同优化,可更加准确合理地衡量非线性鲁棒度。与其他处理不确定性方法相比,MCGDT 不仅弥补了IGDT 中不确定变量描述过于粗糙以及鲁棒系数设定过于主观的不足,还解决了随机规划典型场景不具区间遍历性的问题；

2）基于MCGDT 的风光储联合鲁棒规划模型充分体现了风光荷场景的多态性以及风光消纳率和总投资成本之间的制约关系,兼顾鲁棒准确性与综合目标最优性,实现了更为准确而合理的不确定性规划；

3）CE-RSDE 算法突破了常规群智能优化算法寻优速度与寻优深度的瓶颈,所得结果更为优越而准确,实现了模型的深度寻优与高效求解。

本文提出的基于MCGDT 的风光储联合鲁棒规划模型和CE-RSDE 算法为不确定性电能规划和群智能优化算法提供了新思想。MCGDT 对于含可再生能源的智能电网调度和主动配电网规划等研究也将具有重要的指导意义,并可推广应用到其他不确定性优化领域。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。