基于反转威德曼效应的管道扭转导波监测换能器设计
张 帆,马共立,李 策,王淑娟
(1.哈尔滨工业大学电器与电子可靠性研究所,黑龙江哈尔滨 150001;2.哈尔滨铁路科研所科技有限公司,黑龙江哈尔滨 150006)
0 引言
金属管材、棒材等在服役过程中会出现腐蚀坑、裂纹、穿孔等结构损伤,进而引发严重的安全事故,因此需要定期进行检测或长期实时监测。超声导波作为一种新兴的无损检测技术,以其单点激励、检测距离远、检测效率高等优势,成功应用于在役管道、储罐等大型工业设施的检测中[1-3]。其中,扭转导波在传播过程中,质点沿管道周向振动,对纵向缺陷敏感,且低模数的T(0,1)模态导波具有非频散特性,被广泛应用于管材、棒材缺陷检测[4]。基于磁致伸缩效应的扭转导波激励方法由于换能效率高、换能器结构简单等优势被国内外学者广泛关注。
目前,长距离磁致伸缩超声导波检测系统已在工业现场实现应用。研制可长期安装在工业现场的传感器和无线激励/接收装置,实现远程长期监测是磁致伸缩导波技术的发展趋势。根据威德曼效应,管状、棒状铁磁性材料在正交磁场的作用下,将产生扭转形式的形变(板状铁磁性材料中为水平剪切形式的形变)。因此,用于磁致伸缩SH导波检测的换能器通常由预先磁化的磁致伸缩贴片和曲折线圈构成,分别提供方向垂直的静磁场和交变磁场。但是,偏置磁场强度对磁致伸缩扭转导波换能器换能效率影响明显,预磁化方式提供的偏置磁场较小,导致换能器换能效率低,导波传播距离短[5]。此外,预磁化的磁致伸缩贴片中的剩磁会随时间增加逐渐消退,导致预磁化式的磁致伸缩换能器无法进行长期现场监测。美国西南研究院提出了一种永磁式磁致伸缩扭转导波换能器结构,实现了管道长期监测,但是并未对换能器参数进行研究和优化设计。
针对上述问题,本文设计了管道周向永磁阵列和柔性曲折线圈换能器结构,通过有限元仿真分析永磁铁阵列对偏置磁场的影响,实验证明该换能器能够激励纯净的T(0,1)模态导波,并且能够通过调整磁致伸缩贴片宽度调整换能器中心频率。
1 磁致伸缩扭转导波换能器结构设计
1.1 换能器换能机理
磁致伸缩扭转导波激励与接收是威德曼效应的典型应用,如图1(a)所示,铁磁性管材或棒材在周向静态磁场和轴向动态磁场的共同作用下,将产生扭转形变。图1(b)则给出了另一种激励和接收扭转导波的方法,即将静态磁场和动态磁场的方向改变,同样能够在管材、棒材中激励和接收扭转导波,这一现象称为反转威德曼效应[6]。
基于威德曼效应或反转威德曼效应,在管材、棒材表面通过耦合剂粘贴高磁致伸缩系数的材料,使其在方向垂直的静态磁场和动态磁场共同作用下,即可激励和接收长距离传播的扭转导波。

(a)正威德曼效应
1.2 换能器结构设计
本文通过实验的方式对比2种结构的换能器在铝材料中信号幅值随静磁场变化的规律。实验装置如图2所示,磁致伸缩贴片长25 mm、宽10 mm、厚0.1 mm,粘贴在4 mm厚铝板表面。图2(a)为预磁化方式实验装置示意图,使用霍尔元件测得2块永磁铁N极表面磁感应强度分别为241.6 mT和603.4 mT,线圈长25 mm,宽10 mm。图2(b)为基于威德曼效应的换能器实验装置示意图,线圈长25 mm、宽10 mm。图2(c)为基于反转威德曼效应的换能器实验装置示意图,线圈长25 mm,宽10 mm。线圈均采用线径为0.03 mm的铜制漆包线紧密绕制,激励频率为200 kHz。通过调整电磁铁,使霍尔元件测得的静磁场大小由30 Gs增加至600 Gs,步进值为30 Gs(1 Gs=10-4T)。

(a)预磁化实验装置
换能器为自发自收结构,记录换能器接收到的端面回波信号幅值,实验结果如图3所示,结果表明:
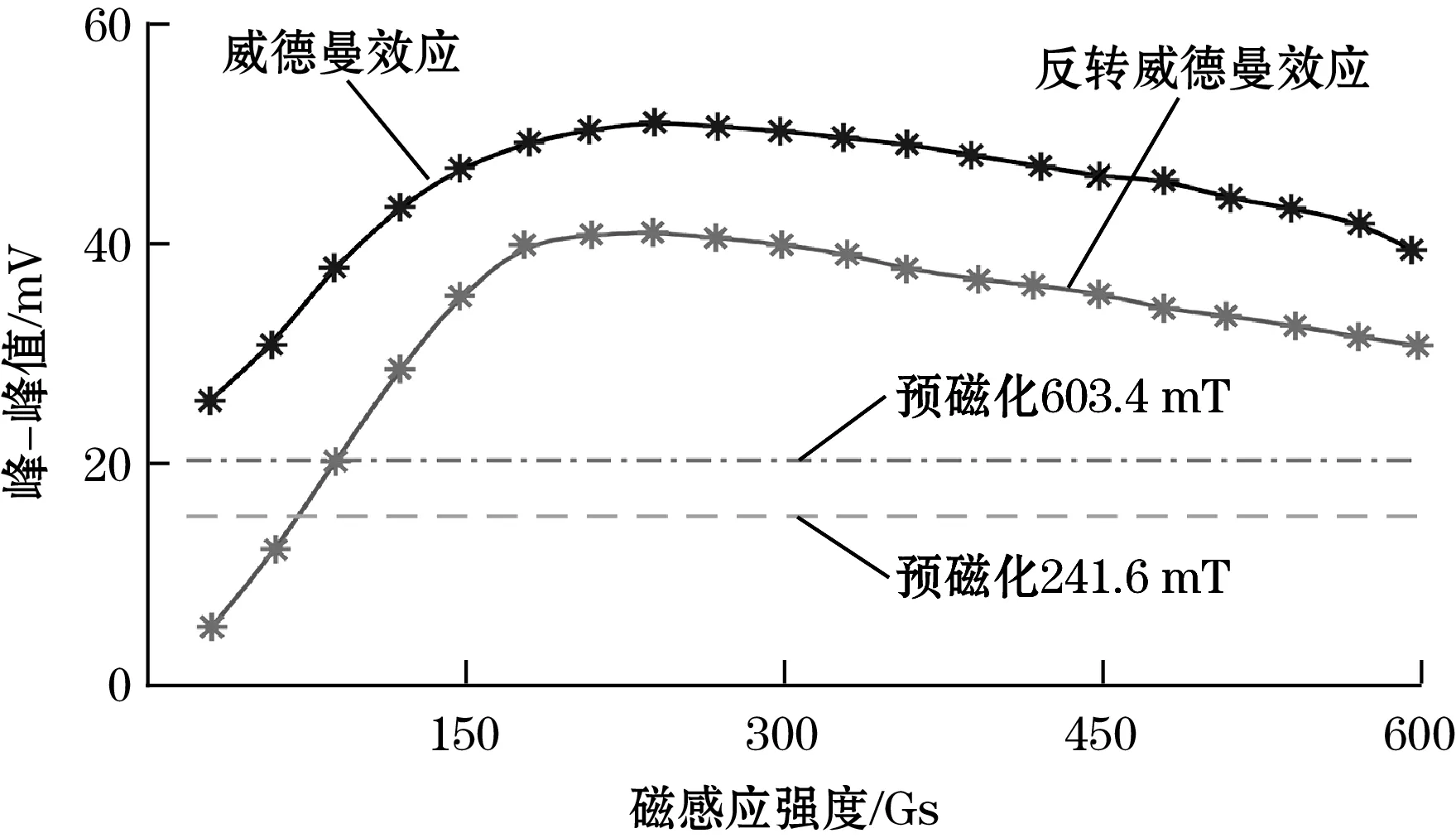
图3 静磁场-幅值曲线
(1)随着预磁化使用的磁铁强度增加,接收到的端面信号幅值增加,且预磁化方式接收到的导波端面信号幅值远小于最佳偏置磁场下基于威德曼效应和反转威德曼效应的换能器接收到的导波端面信号幅值。
(2)随着偏置磁场强度增加,导波端面回波信号幅值呈现出先增加后减小的趋势。因此,为了获得最大换能效率,需要将偏置磁场设置为最佳偏置磁场。
(3)偏置磁场大小相同的情况下,基于威德曼效应的换能器换能效率略大于基于反转威德曼效应的换能器。
考虑到管状、棒状试件中难以通过永磁体产生均匀的周向静磁场,且在最佳偏置磁场条件下,2种换能器结构激励和接收的扭转导波幅值接近,因此采用基于反转威德曼效应的换能器结构。如图4所示,将永磁铁沿管道周向排布,永磁铁沿管道轴向方向充磁,产生轴向静磁场,柔性PCB线圈在磁致伸缩贴片上下表面交替排布,通入交流脉冲信号后产生周向动态磁场。
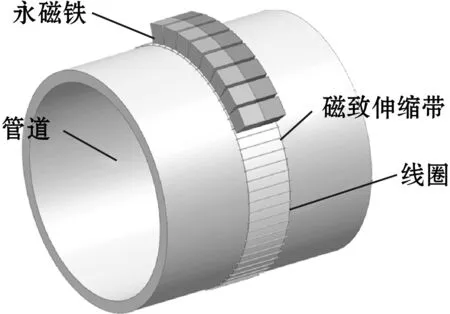
图4 基于反转威德曼效应换能器结构
2 永磁铁阵列参数设计
2.1 静磁场有限元建模
为了通过永磁铁阵列获得最佳偏置磁场,使用COMSOL Multiphysics软件建立换能器静磁场有限元模型,仿真分析永磁铁尺寸、提离距离对偏置磁场的影响。仿真模型如图5所示,相关参数如表1所示。使用振动样品磁强计测量本文所使用的铁钴合金HB曲线,如图6所示。

图5 静磁场仿真模型
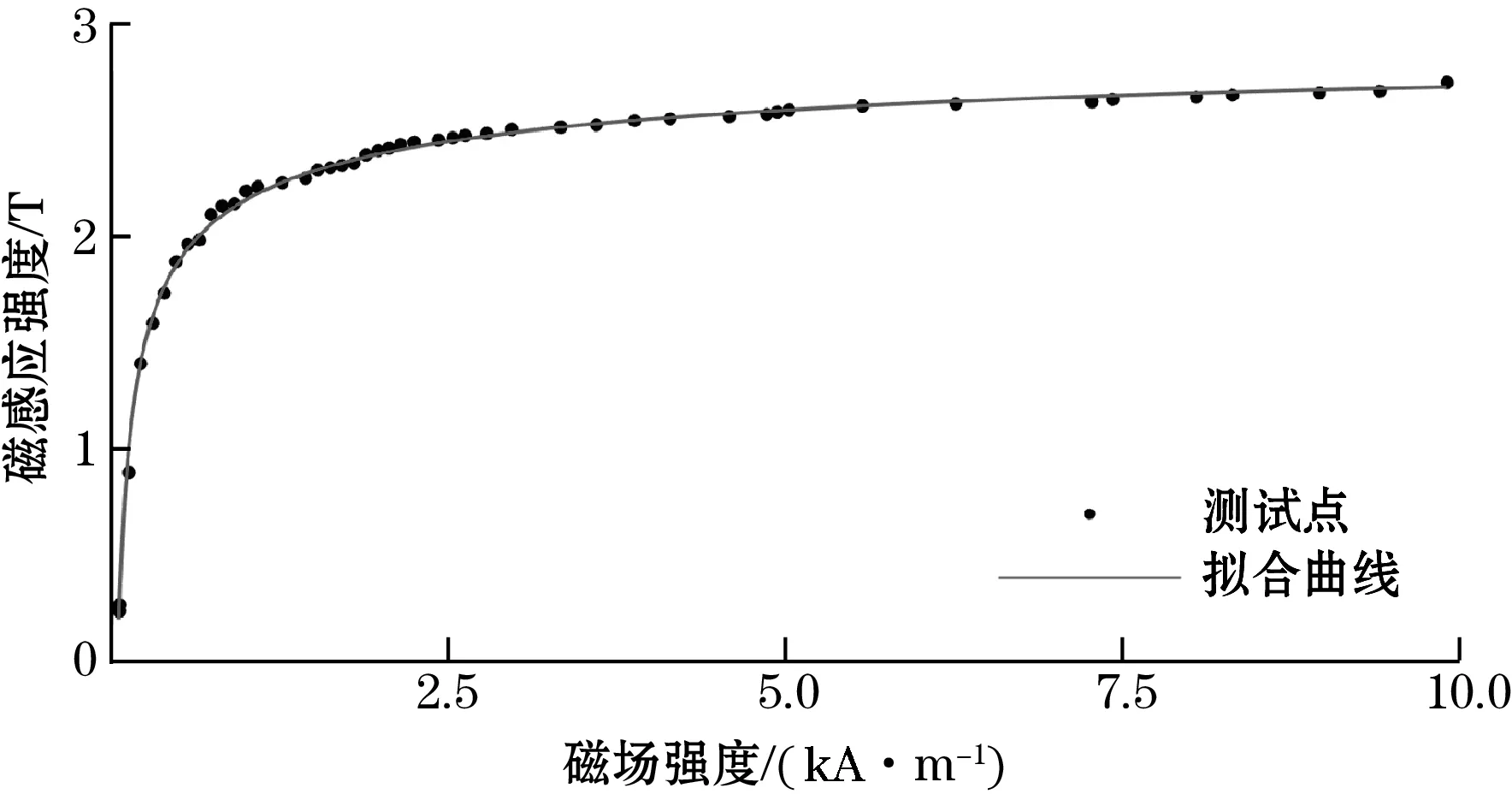
图6 磁致伸缩带HB曲线

表1 仿真模型具体参数
2.2 静磁场仿真分析
偏置磁场由多个永磁铁沿管道周向排列,每个永磁铁沿管道周向方向尺寸10 mm,永磁铁共30个。
为了研究磁铁径向尺寸和轴向尺寸对静磁场的影响,采用控制变量法对上述2个参数进行仿真。
首先,对永磁铁轴向尺寸进行仿真,以5 mm为步长,分别计算永磁铁轴向尺寸5~30 mm时磁致伸缩贴片中的偏置磁场。模型其他参数如表1所示,其中永磁铁径向尺寸为1 mm、提离距离为0.2 mm。磁致伸缩贴片中的偏置磁场如图7所示,其中图7(a)为静磁场轴向分量沿管道周向方向的分布,图7(b)为静磁场轴向分量沿管道轴向方向的分布。结果表明,永磁铁轴向尺寸对偏置磁场分布的均匀性和大小影响明显。当永磁铁轴向尺寸小于磁致伸缩贴片宽度时,磁致伸缩贴片中静磁场轴向分量在管道周向和轴向分布均不均匀,波动明显;且随着永磁铁轴向尺寸增加,静磁场均匀性明显改善,磁场大小降低。当永磁铁轴向尺寸大于磁致伸缩贴片宽度时,静磁场均匀性、大小基本相同。因此,为了获得分布均匀的偏置磁场,需要使永磁铁轴向尺寸大于磁致伸缩贴片宽度。

(a)管道周向的轴向分量
然后,对永磁铁径向尺寸进行仿真,以1 mm为步长,分别计算永磁铁径向尺寸1~5 mm时磁致伸缩贴片中的偏置磁场。模型其他参数如表1所示,其中永磁铁轴向尺寸为30 mm、提离距离为0.2 mm。磁致伸缩贴片中的偏置磁场如图8所示,其中图8(a)为静磁场轴向分量沿管道周向的分布,图8(b)为静磁场轴向分量沿管道轴向的分布。结果表明,永磁铁径向尺寸对偏置磁场大小影响明显,对磁场分布均匀性几乎无影响。随着永磁铁轴向尺寸增加,偏置磁场轴向分量沿管道周向和轴向2个方向的分布均匀性几乎不变,磁场大小线性增加。因此,可通过调整永磁铁径向尺寸,调整偏置磁场大小。
最后,对永磁铁提离距离进行仿真,以1 mm为步长,分别计算永磁铁提离距离0~5 mm时磁致伸缩贴片中的偏置磁场。模型其他参数如表1所示,其中永磁铁轴向尺寸为30 mm、径向尺寸为1 mm。磁致伸缩贴片中的偏置磁场如图9所示,其中图9(a)为静磁场轴向分量沿管道周向方向的分布,图9(b)为静磁场轴向分量沿管道轴向方向的分布。结果表明,永磁铁提离距离对偏置磁场大小影响明显,对磁场分布均匀性几乎无影响。
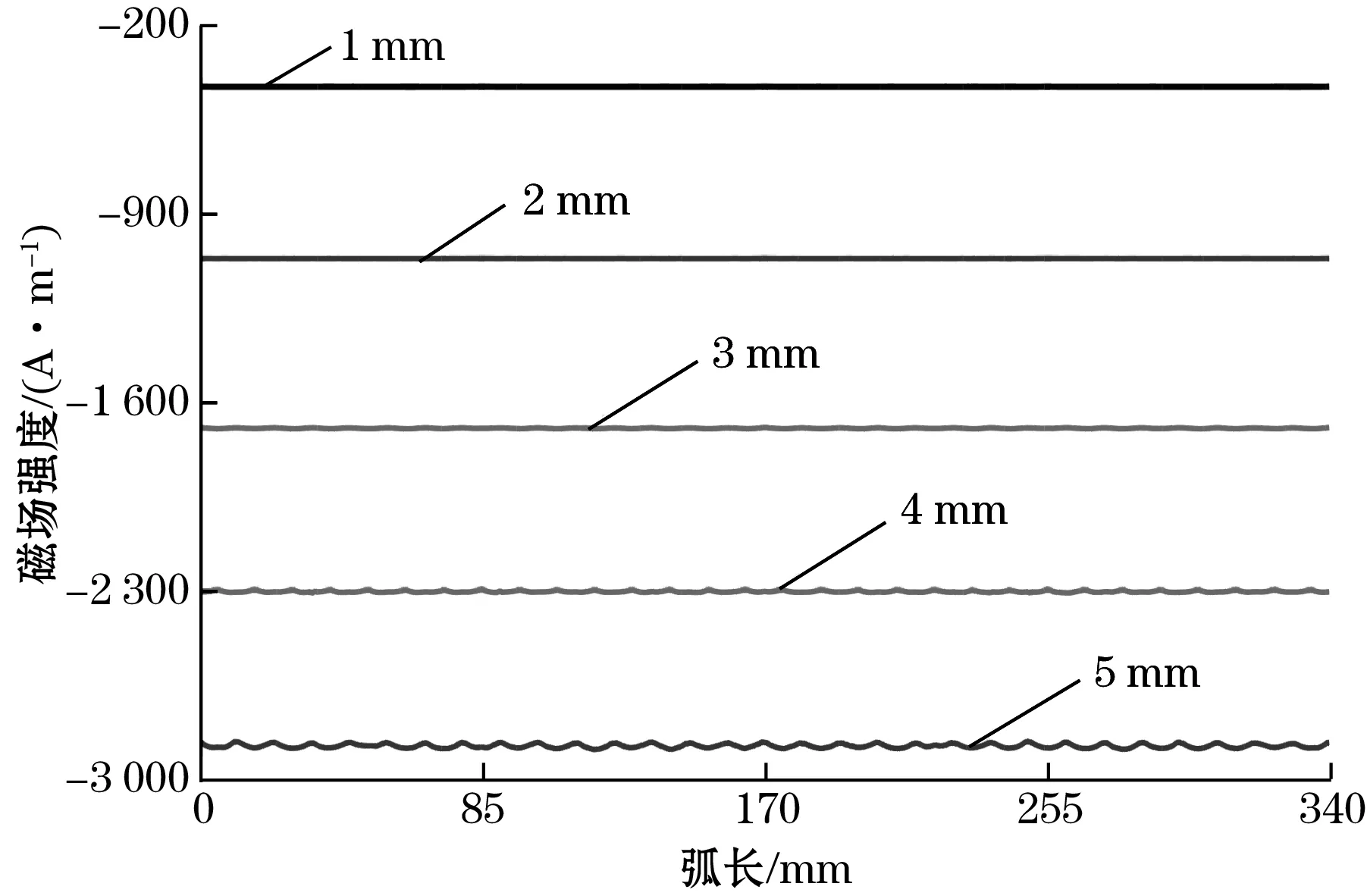
(a)管道周向的轴向分量
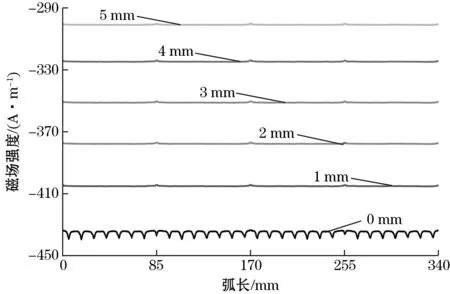
(a)管道周向的轴向分量
随着永磁铁提离距离增加,偏置磁场轴向分量沿管道周向和轴向2个方向的分布均匀性几乎不变,磁场大小线性减小。因此,可通过调整永磁铁提离距离,调整偏置磁场大小。
综上所述,为了保证偏置磁场的均匀性,永磁铁轴向尺寸需大于磁致伸缩贴片的宽度;偏置磁场的大小,可以通过调整永磁铁径向尺寸和提离距离进行调节。
3 扭转导波激励与接收实验
为了验证本文提出的换能器结构激励扭转导波的可行性,在厚度为2 mm的铝管上进行实验,实验装置如图10所示。将4 mm宽的磁致伸缩贴片环绕在管道表面,使用环氧树脂进行粘接。激励线圈为柔性PCB曲折线圈,相邻导线族间距为10 mm,导线族宽度为2 mm,交替分布在磁致伸缩贴片上下表面。将轴向尺寸为15 mm、径向尺寸为10 mm的N35钕铁硼永磁铁(剩磁约1.2 T)放置在磁致伸缩贴片上方,通过调整永磁铁的提离距离,改变磁致伸缩贴片中偏置磁场的大小。
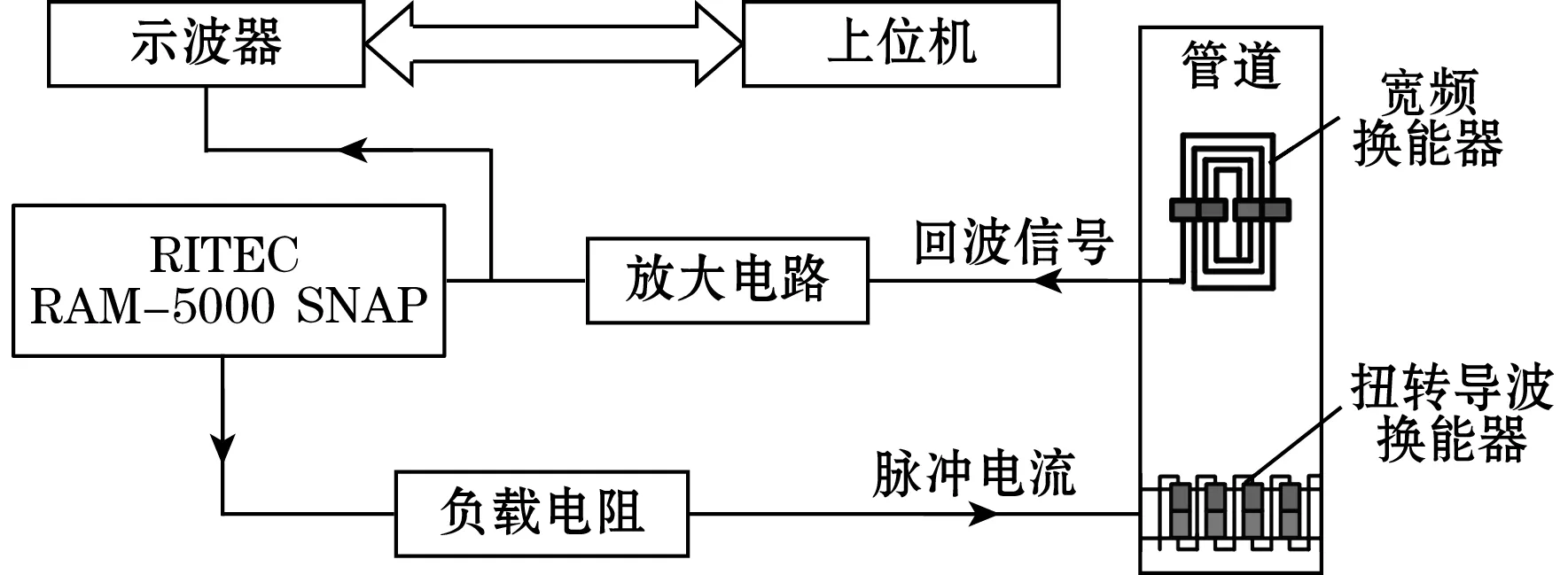
图10 基于反转威德曼效应的实验装置
使用RITEC RAM-5000 SNAP非线性高能超声测试系统进行激励与接收,激励频率为300 kHz,接收换能器为周期永磁铁型宽频电磁超声换能器。
接收信号如图11所示,发射换能器与接收换能器间距为45 mm,接收到的超声导波信号对应时间为142.8 μs,声速为3 151 m/s,与铝管中T(0,1)模态导波的理论声速基本一致。因此,本文提出的换能器结构,能够在管道中激励纯净的T(0,1)模态导波。

图11 反转威德曼效应在管道中激励SH导波
偏置磁场过大或者过小,均会导致磁致伸缩导波换能器换能效率降低。为了获取最佳偏置磁场,将永磁铁的提离距离从36 mm逐渐降低至0 mm,步进值为2 mm。由于永磁铁距离磁致伸缩贴片较近时,磁致伸缩贴片会被磁化,为了避免提离距离较大时磁致伸缩贴片中剩磁对实验结果的影响,将永磁铁从较大的提离位置开始逐渐减小。记录永磁铁不同提离距离对应的接收信号幅值,结果如图12所示,随着提离距离逐渐降低,接收到的超声导波信号幅值呈现先增加后减小的趋势。

图12 提离高度-信号幅值曲线
通过调整永磁铁的提离距离,能够有效调整磁致伸缩贴片中偏置磁场大小,选择恰当的提离距离,能够使换能器换能效率达到最高水平。
4 换能器频率响应特性实验
使用超声导波检测技术对工业设备进行检测时,通常采集多个频率的导波检测信号进行分析。因此,研究换能器中心频率影响因素具有重要意义。理想情况下,对于有限宽度的均匀力源,激励的超声导波信号幅值最大值对应的波长,满足力源宽度等于(n+0.5)倍波长,其中n为非负整数。这可以直观地理解为力源宽度小于波长的1/2时,力源宽度逐渐增加,每一个点力源产生的位移对于和位移增加都是有贡献的,所以力源宽度增加,即位移增加,接收信号幅值增加。当力源宽度增加至1/2波长后,继续增加的点力源与相距为1/2波长的点力源产生的位移恰好相互抵消,因此随着力源宽度增加,和位移减小,接收信号幅值降低。
磁致伸缩贴片式换能器通过磁致伸缩贴片形变产生超声导波,因此试件表面力源分布与磁致伸缩贴片几何形状相似,即能够通过调整磁致伸缩贴片宽度改变力源宽度,调整换能器中心频率。本文分别使用宽度为4、6、8、10、12 mm的磁致伸缩贴片,在200~600 kHz的频率范围内进行扭转导波激励,其中激励频率步进值为20 kHz。记录各磁致伸缩贴片在不同频率下接收信号的幅值,结果如图13所示。结果表明,各接收信号幅值与激励频率关系曲线峰值对应频率约为380、300、220、450、380 kHz,对应波长约为8.4、10.7、14.5、7.1、8.4 mm。由宽度为4、6、8 mm的磁致伸缩贴片的结果可知,随着磁致伸缩贴片宽度增加,接收信号峰值对应的激励频率逐渐降低,且满足磁致伸缩贴片宽度约1/2波长。根据上述关系,当磁致伸缩贴片宽度为10 mm和12 mm时,接收信号峰值对应的激励频率约为160 kHz和135 kHz,不在本实验激励频率范围内,无法通过实验结果观测。但是,其接收信号第2个峰值对应的波长,满足磁致伸缩贴片宽度约等于1.5倍波长,这一对应关系进一步证明磁致伸缩贴片宽度为10 mm和12 mm时,接收信号第1个峰值对应的波长约为磁致伸缩贴片宽度的2倍。

图13 导波换能器的频率响应特性
5 结束语
针对预磁化式磁致伸缩导波换能器无法应用于长期监测的不足,本文提出了一种基于反转威德曼效应的周向永磁阵列式换能器结构。通过有限元仿真分析了永磁铁尺寸和提离距离对偏置磁场的影响,并实验验证本文提出的换能器结构激励扭转导波的可行性。具体结论如下:
(1)为了保证偏置磁场均匀性,永磁铁轴向尺寸须大于磁致伸缩贴片宽度;磁致伸缩贴片中偏置磁场大小随永磁铁径向尺寸增加而增加,随永磁铁提离距离增加而减小。因此,可以通过调节永磁铁径向尺寸和提离距离,调节偏置磁场大小,直至换能效率达到最高。本文通过扭转导波激励实验证明了调节永磁铁提离距离,能够使换能器达到最佳换能效率。
(2)实验证明本文提出的换能器能激励纯净的T(0,1)模态导波,适用于工业管道长期健康监测。
(3)实验证明本文设计的换能器中心频率与磁致伸缩贴片宽度有关,中心频率对应的波长,满足磁致伸缩贴片宽度约为1/2波长。因此,通过调整磁致伸缩贴片宽度,能够设计预期中心频率的换能器。

