机器人关节扭矩传感器的设计与性能分析
张文明,杨 冬
(河北工业大学机械工程学院,天津 300401)
0 引言
扭矩传感器又称扭力传感器,是一种常用的检测仪器,被广泛应用于汽车、机器人等机械类行业中。2020年出版的《直列式扭矩传感器市场现状及未来发展趋势报告》中的数据显示,扭矩传感器的消费数量同比增长了16.7%。朱弟发等[1]为提高机器人的安全性以轮幅式扭矩传感器为参考,设计了一种关节输出轴与传感器一体化的结构形式,利用响应面法对结构参数进行优化分析,结果使其抗过载能力和线性度得到了提升。金力等[2]在协作机器人中采用内嵌扭矩传感器的紧凑型一体化关节,提高了机器人力控制的安全性和关节负载能力。李志鹏等[3]分析了温度、压力、扭矩传感器在研发过程中所遇到的困难,并对传感器在汽车电子领域中的发展前景进行了预测。于振等[4]设计了一种立式扭矩传感器校准系统,改善了扭矩传感器中存在的校准效率低、误差大的缺点。M. Li等[5]针对传统的刚性扭矩传感器中存在不符合规范、在可穿戴应用中存在兼容性等问题,设计了一种软压阻式应变传感器,该传感器可以实际测量关节的转角和扭矩。
轮辐式关节扭矩传感器具备便于拆卸的特点[6]。本文通过仿真分析对传感器结构进行了优化。然后分析了应变片的最佳粘贴位置,最后由传感器测定的实验数据表明:该传感器具备较高的灵敏度和线性度,且迟滞误差较小,满足机器人对扭矩传感器使用的参数要求。
1 传感器的结构设计及优化分析
1.1 传感器结构设计及优化
依照相似产品,初步确定弹性体的尺寸参数,使其满足作为弹性体的强度要求。扭矩传感器的最大负载扭矩为100 N·m。材料采用制造扭矩传感器的常用材料2024超硬铝合金,它具有易加工、耐腐蚀、屈强比高等优点。其弹性模量为73 GPa,屈服极限为75.8 MPa。传感器弹性体结构如图1所示。

图1 传感器弹性体结构图
初选内轮缘内直径为20 mm,外直径为 60 mm;外轮缘内直径为80 mm,外直径为100 mm,内外轮缘厚度均为8 mm。轮辐的参数:宽度×长度×厚度为16 mm×20 mm×8 mm。首先将弹性体模型以parasolid格式导入workbench软件中,然后对模型进行参数给定、划分六面体网格,并施加100 N·m的扭矩,分析结果如图2所示。
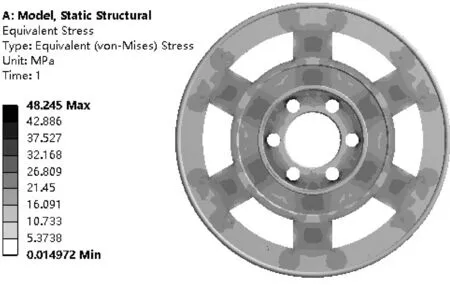
图2 优化前的仿真结果
由图2可知:轮辐式扭矩传感器最大应力为48.245 MPa,小于屈服强度75.8 MPa,此时的安全系数为1.57,有较大优化空间。根据应力的分布特点,将轮辐的宽度作为优化对象。把轮辐宽度改为12 mm,重复操作,优化后的结果如图3所示。

图3 优化后的仿真结果
优化后的轮辐式扭矩传感器最大应力为62.475 MPa,材料的屈服极限为75.8 MPa,其安全系数为1.21。在保证扭矩传感器足够安全的条件下实现了优化。因此,传感器的轮辐宽度定为12 mm。安装在机器人旋转关节上的扭矩传感器如图4所示。

图4 扭矩传感器
1.2 应变片粘贴位置分析
当传感器受到垂直于纸面方向上的扭矩T作用时,轮辐受到剪切应力Q和弯矩M的共同作用。由于传感器轮辐结构呈对称分布,因此只分析其中的一个轮辐即可,根据材料力学知识对轮辐进行受力分析,轮辐受力分析如图5所示。

图5 轮辐受力分析
对轮缘的中心点取力矩可知:
6[Q(x+r)+M]-T=0
(1)
移项后得:
M=T/6-Q(x+r)
(2)
式中x为轮辐截面到内轮缘外圈半径r的长度。
假设轮辐与内、外轮缘的连接处为刚性,则两端连接处的转角α=0,此时在轮辐处施加M0(x)=1的单位力偶矩,则由莫尔定理可得:
(3)
式中:α为转角;l为轮辐长度;E为弹性模量;I为转动惯量。
由此可知:
(4)
将式(4)代入式(1)中,可得:
(5)
当x=l/2时,轮辐的弯矩为0,可以消除弯曲影响。
矩形截面梁弯曲剪应力计算公式为
(6)
式中:Ix为矩形截面对中性轴的转动惯量;h为轮辐高度。
因为Ix=bh3/12。当y=0时取得剪应力的最大值。τmax=3Q/(2bh),由纯剪切应力状态可知,在y=0的中性面上,与x轴成45°方向上,主应力和最大剪切应力相等,因此可以确定应变片的粘贴位置为轮辐中心位置且与轮辐成正负45°方向上的中性面上。
2 实验测试及性能分析
2.1 传感器桥路设计分析
为了避免除扭矩以外的其他因素对应变片电阻值的影响,在轮辐表面粘贴2组共12片应变片,每组应变片采用惠斯登全桥电路与传感器相连接,惠斯登全桥电路如图6所示。

图6 惠斯登全桥电路
对惠斯登全桥电路进行分析,可得输出电压为
(7)

因此,可以求得其电流为

(8)
所以当Ig=0时,即R1R4=R2R3;因此,在负载扭矩为0时,电桥处于平衡状态。当各应变片的电阻值发生微小变化时,即ΔR1、ΔR2、ΔR3、ΔR4,由欧姆定律可知输出端的电流、电压等参数也会产生相应变化。输出端的电压为
(9)
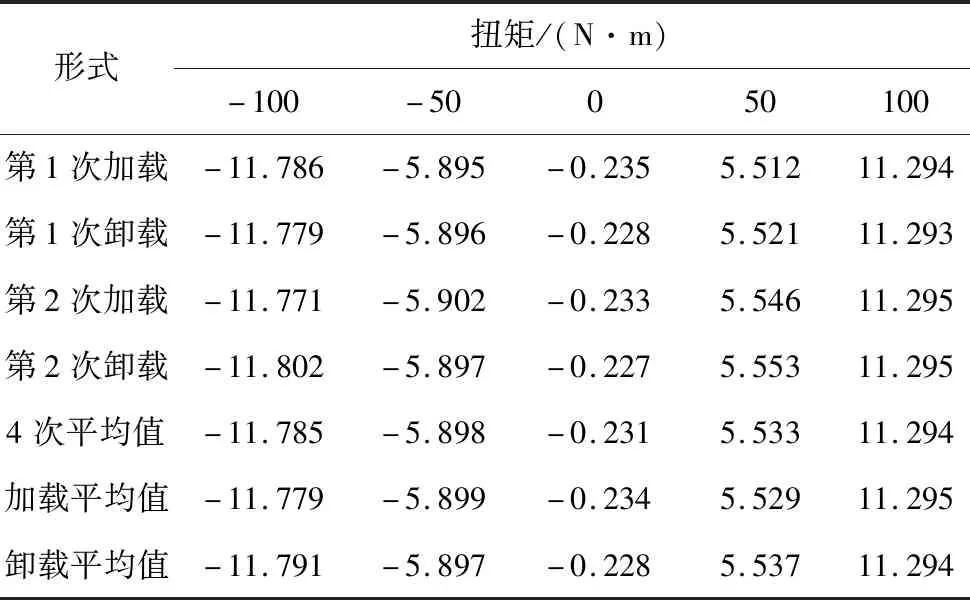
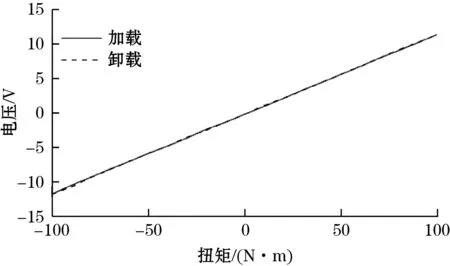
由于ΔR< (10) 又因为实验是采用阻值相同的应变片组成的桥臂,即R1=R2=R3=R4=R,继续化简得: (11) 根据应变原理可知ε1=-ε2=ε3=-ε4,即ΔR1= -ΔR2=ΔR3=-ΔR4,则有: (12) 式中:K0为金属电阻丝的灵敏系数;ε为应变。 (13) (14) 式中μ为泊松系数。 由式(14)可知:输入扭矩与输出电压成线性关系,若已知输出电压,则可以计算输入的扭矩大小[7]。 实验时,根据扭矩的影响因素来实现扭矩的加载和卸载,具体包括改变力臂长度和砝码个数。无论是加载状态还是卸载状态,都是以10 N·m为间隔实现全量程范围的扭矩增加或减少,并进行2次正向加载、2次反向卸载实验,记录获得的实验数据。在读取输出电压时,要注意等到示数稳定后再记录实验数据。将4次实验获得的输出电压取平均值,以减少偶然现象对实验结果的影响,部分实验数据如表1所示。 表1 实验测试得到的输出电压 V 传感器性能的指标主要包括线性度、迟滞性等。对测量出的数据进行计算可以得到每个性能指标。以输出电压为纵坐标,输入扭矩为横坐标。然后利用最小二乘法对实验测量出的数据进行拟合,拟合结果如图7 所示。数据点都落在拟合直线上且偏差很小,说明扭矩传感器的线性度良好[8]。 图7 线性度分析 同样地,分别以加载、卸载时的输出电压为纵坐标,输入扭矩为横坐标,进行数据取点和直线绘制。卸载时的输入扭矩与加载时输入扭矩一一对应,在加载、卸载相同扭矩输入的情况下,通过比较输出电压分析迟滞性能指标,如图8所示。代表加载的实线和代表卸载的虚线几乎重合,说明卸载过程中的迟滞现象不明显,证明了扭矩传感器的结构设计具备合理性[9]。 图8 迟滞分析 量化分析可以更加准确反映出扭矩传感器的各项参数性能。由公式计算得出传感器的各项性能指标如表2所示。 表2 扭矩传感器样机性能指标 本文研究了一种用于机器人的关节扭矩传感器。通过公式推导和材料力学知识确定了应变片的最佳粘贴位置。以安全系数为参考并利用有限元分析方法对扭矩传感器进行了优化。由惠斯登全桥电路测得的数据分析可知,输出电压和输入扭矩成线性关系。实验数据表明:扭矩传感器的线性度、迟滞误差等性能指标较为优良,满足机器人精确控制对扭矩传感器的参数要求。
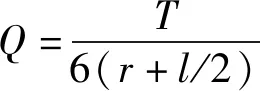
2.2 实验测试过程
2.3 测试数据分析


3 结束语

