用于轮胎胎冠裂纹检测的磁致伸缩触觉传感器研究
赵智忠,沈 鑫,王博文,王志强
(1.河北工业大学,省部共建电工装备可靠性与智能化国家重点实验室,河北省电磁场与电器可靠性重点实验室,天津 300130;2.河北工业大学土木与交通学院,天津 300130)
0 引言
轮胎的健康状况对于安全行车具有重要意义[1]。胎冠裂纹使轮胎与地面的附着力下降同时也可能导致高速行驶下的汽车爆胎,影响行车安全。机动车运行安全技术条件中规定:轮胎不应有影响使用的缺损[2],当轮胎出现长度大于6 mm或者深度大于3 mm裂纹时建议更换。
轮胎主要由胎冠与胎侧组成,胎侧没有花纹,缺陷可以人眼识别;胎冠正常花纹复杂且车胎老化后细小裂纹繁多,不符合要求的裂纹可能漏检[3]。依靠人工检测这种识别方式检测轮胎缺陷效果差,为了提高检测效率,一些算法已经应用到实际生产中。孙虹霞将轮胎X光图像转化到频域对缺陷进行定位[4];吴则举团队提出了基于改进的FasterR-CNN来实现轮胎缺陷的自动检测[5];文献[6]开发了一种深度卷积稀疏编码网络用于轮胎缺陷分类。以上传统算法在小样本数据集中测试准确率低,仅从视觉方面检测轮胎缺陷。有必要设计触觉传感器,视触融合检测轮胎缺陷,将会提高检测结果的可信度。
现有的触觉传感器有多种类型,依据传感器的敏感元件不同可将触觉传感器分为光纤型、压电型、电容型、压阻型[7-8]。光纤传感器测量精度高,但其制造工艺要求高价格昂贵[9],压电传感器具有良好的动态性能,但其不能保持输出电压的稳定[10]。电容型传感器体积较小,但通常需要额外的信号放大和处理电路增加铺设成本[11]。压阻型传感器制造工艺简单,灵敏度高,但输出特性受环境温度影响大,需外加温度补偿[12]。
以铁镓合金片为敏感元件设计了用于轮胎胎冠裂纹检测的磁致伸缩触觉传感器阵列。铁镓合金制造的金属片脆性小,能够承受冲击机械载荷。片状铁镓悬臂梁的换能密度可以达到22 mW/cm3,这是压电材料不可比拟的[13]。
本文基于动物毛发的感知机理,使用Galfenol薄片、霍尔元件、永磁体为主要元件,设计了一种采集深度信息的触觉传感器阵列,用于检测轮胎胎冠裂纹。检测时传感器在轮胎表面滑动得到反映正常花纹与裂纹信息的电压数据,通过MATLAB算法从这些数据中识别所需的裂纹数据并计算裂纹的深度。
1 传感器设计
1.1 传感器结构
触觉使动物感知外部世界信息,例如海豹胡须可以感应周边动物在水中产生的尾波,以此判断捕猎对象的大小[14]。基于动物毛发感知结构设计了传感单元的基本结构[15]。如图1(a)所示,动物毛发受力弯曲,神经元感受到毛发变化传递给大脑进行处理。根据这种机理设计了传感单元的基本结构,如图1(b)所示。Galfenol合金薄片像动物的毛发受力弯曲,霍尔元件作为神经元接收磁信号转化为电信号传递给计算机。
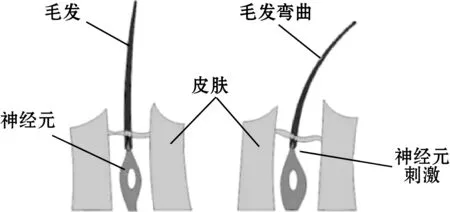
(a)毛发结构
传感单元由Galfenol薄片、钕铁硼(Nd2Fe14B)永磁体、EQ-730L型霍尔元件、刚性树脂基底、铜锌合金触头、伸缩杆和缓振弹簧组成。为使测量过程稳定平滑,传感单元与轮胎接触部分采用球形触头。它的半径为0.15 mm,宽度大于0.35 mm的裂纹可以有效识别。采用多晶取向<100>的Fe83Ga17单层片状合金作为传感单元的悬臂梁,一端固定在树脂基底上另一端为自由端,2块参数完全相同的平行永磁体提供偏置磁场。触觉传感器基于磁致伸缩逆效应,当处于均匀磁场中的Galfenol薄片受到外力作用时磁导率发生改变,霍尔元件周围的磁感应强度发生变化,输出的电压信号也会发生相应变化。
1.2 Galfenol薄片长度的选择
使用COMSOL Multiphysics有限元软件对Galfenol薄片受力仿真分析,结果如图2所示。自由端施加0.2~1 N固定力,在10~20 mm范围内,长度选择12 mm时输出结果最理想。
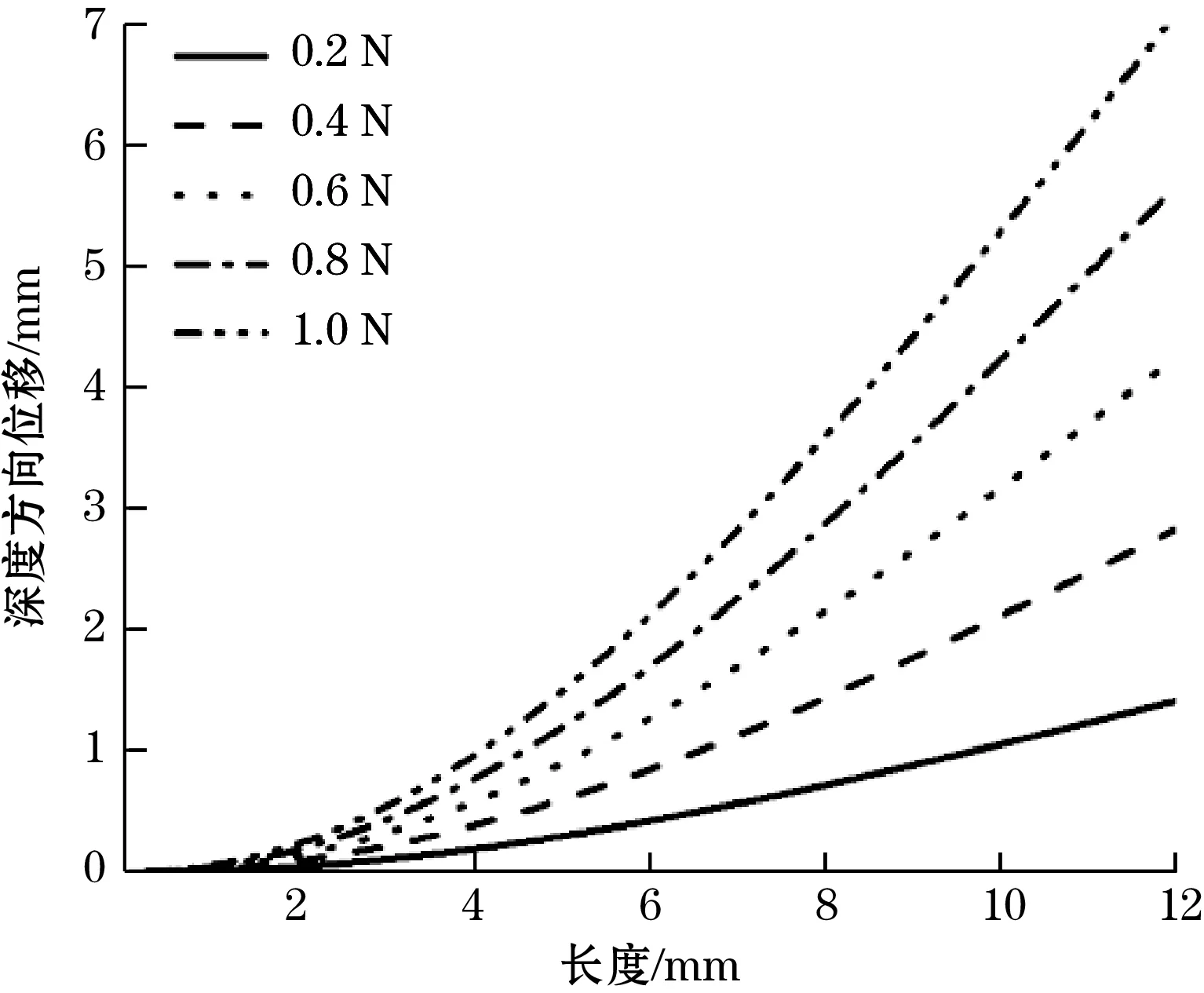
图2 Galfenol薄片长度与深度方向位移的关系
将厚度0.1 mm的Galfenol薄片切割成宽度为3 mm,长度分别为10、12、15 mm的矩形薄片。只改变Galfenol薄片长度时自由端施加力,得到受力与输出电压关系。实验施加0~0.8 N力,步长为0.1 N,为保证实验的可靠性,每个实验点测量10次取平均值,如图3所示。长度为10 mm的悬臂梁电压输出幅值小,测量噪声及误差对有效数据干扰大。当悬臂梁长度设置为15 mm时,弹性不足,测力范围小,传感器恢复困难。综上悬臂梁长度设置为12 mm可以保证传感单元在一定的测力范围有较高的灵敏度。

图3 不同长度Galfenol片输出电压与压力的关系
1.3 传感阵列的设计与制作
传感单元只能检测轮胎花纹深度,无法完成轮胎裂纹的识别,通过一次滑动有效识别裂纹至少需要3个传感单元。虽然各传感单元之间存在相互磁场干扰,但磁力线在Galfenol薄片内部主要沿着长度方向传播。传感单元间距大于5 mm时这种影响消失,施加力大小为0.5 N时,各单元相对误差小于2.5%。制备的1×3磁致伸缩传感器阵列如图4所示,传感器阵列的长宽高为18 mm×15 mm×12 mm,传感单元触头间距为6 mm。

图4 传感器阵列
霍尔元件的3个引脚焊接在长17.96 mm、宽7.62 mm、厚1.60 mm的印刷电路板PCB(printed circuit board)上。霍尔元件的3个引脚(电源VCC、接地GND、信号输出SIGNAL),置入PCB板相应过孔,用焊锡固定,信号输出端过孔连接信号采集装置。工作时信号采集设备同时采集3个传感单元输出的电压信号,经过计算机处理可以获得轮胎胎冠裂纹信息。
2 传感单元的输出特性模型
2.1 接触力检测模型
传感器内部永磁体提供偏置磁场,当悬臂梁未受力时,F=0,S=0,霍尔元件输出电压初始值为
Vref=μKHKCH
(1)
式中:μ为铁镓合金的磁导率;KH为霍尔元件的磁电转化系数;KC为霍尔元件检测铁镓合金内磁场的损耗系数;H为偏置磁场,这里认为偏置磁场是定值。
传感单元输出电压可以表示为
UH=KHKCBGal
(2)
式中BGal为材料内部的平均磁感应强度。
铁镓材料的磁致伸缩逆效应本构方程见式(3)和式(4),该方程描述了磁致伸缩材料的磁机耦合特性。
ε=d33H+σ/E
(3)
BGal=d33σ+μH
(4)
式中:ε为铁镓合金片长度方向的总应变;d33为动态磁致伸缩系数;σ为外加应力;E为磁致伸缩材料的杨氏模量。
悬臂梁为长方体,矩形对于中线(垂直于h边的中轴线)的惯性矩I为
(5)
式中:b、h分别悬臂梁的宽、高。
悬臂梁在受到应力弯曲时高度z处沿悬臂梁的长度方向的力和受力点处的力F之间的关系为
σ=F(x-l)z/I
(6)
悬臂梁所受的平均压应力为
(7)
传感单元输出电压为实际电压与初始电压的差:
U=UH-Vref
(8)
把式(1)和式(2)代入式(8)得,传感单元的输出电压为
U=Kam(KHKCBGal-μKHKCH)
(9)
式中:Kam为模型所需的可调放大倍数;d33为实验测量值。
采用Kam来调节d33的测量误差,把式(5)和式(7)代入式(9)得:
(10)
式中:Kam=17;KH=130 mV/mT;KC=4.28×10-3;d33=3.01×10-8T/GPa。
式(10)为传感单元应力与输出电压的表达式,由式(10)可知,传感单元输出电压U与受力F成正比。
2.2 胎冠裂纹检测模型
胡克定律解释了线性系统内力与位移的关系。传感器触头连接缓振弹簧,这使得传感器悬臂梁的等效弹性系数K发生变化。传感器受力F深度方向的位移为S,t和x分别代表缓振弹簧和悬臂梁。悬臂梁与缓振弹簧等效为2个弹簧串联,由胡克定律得串联弹簧的弹性系数K为
(11)
由欧拉-伯努利梁结构动力学理论可得悬臂梁挠度与受力的关系:
(12)
自由端x取最大值此时挠度为
(13)
悬臂梁在弹性范围内的等效弹性系数:
(14)
竖向位移与受力关系:
(15)
K为常数,在弹性形变范围内,深度方向位移与受力满足线性关系。将式(10)代入式(15)得传感单元输出电压与触头位移的关系为
(16)
式(18)为传感单元输出电压U与触头深度方向位移S的关系式,输出电压与位移成正比。
3 触觉传感器特性测试
磁致伸缩触觉传感器输出特性测试系统如图5所示,主要由数据采集卡、直流稳压电源、压力测试机、滑轨等组成。直流稳压电源为霍尔元件提供5 V的工作电压,数据采集卡采集霍尔元件输出的动态信号。经过PC处理得到胎冠裂纹信息。

图5 传感器输出特性测试系统
3.1 传感单元静态测试
通过电子游标卡尺和压力测试机给传感单元施加0~0.8 N固定力,每次增加0.1 N,每增加0.1 N力触头位移增加0.7 mm,如图6所示。当力增加到0.8 N时输出电压增幅变缓,这是磁导率变化接近饱和导致的。由此知传感单元在0~0.7 N对应触头位移0~4.9 mm范围内具有较平稳的静态输出特性,灵敏度可达170.5 mV/N,施加不同力时响应时间和恢复时间小于80 ms。因为下压深度超过4.9 mm传感单元输出非线性且下压深度大会导致悬臂梁恢复存在困难,故将传感单元触头的最大下压深度设置为4.9 mm,保证传感单元工作时的稳定性。

图6 输出电压与触头深度方向位移关系
3.2 传感单元动态测试
KH-01步进电机控制器驱动装有传感器的滑轨工作台匀速在3D打印制作的光滑花纹上滑动,如图7所示。

图7 传感器与实验模块接触示意图
开始传感器触头处于下压状态与模型平面接触,为防止传感器非触头部分与胎面接触增大摩擦,实际下压深度4.8 mm。随着滑轨的移动深度发生变化,下压深度与花纹深度对应表如表1所示。测试结果如图8所示,实验值与式(16)得到的计算值误差小于2%,量测噪声在允许偏差范围内。
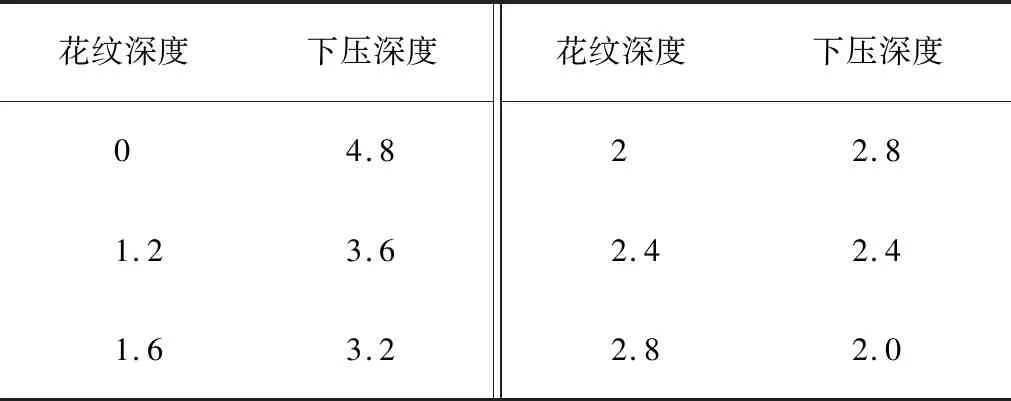
表1 模型花纹深度与触头下压深度 mm

图8 传感单元动态测试输出电压
4 轮胎裂纹测量
选取典型的带有裂纹的轮胎胎冠花纹块并固定,将传感器固定在滑轨工作台,触觉传感器阵列触头下压(4.8 mm)放置。传感单元1、2、3滑过的轨迹如图9所示,由图9可知,传感单元1和2接触裂纹D,传感单元3滑过正常花纹A与B。
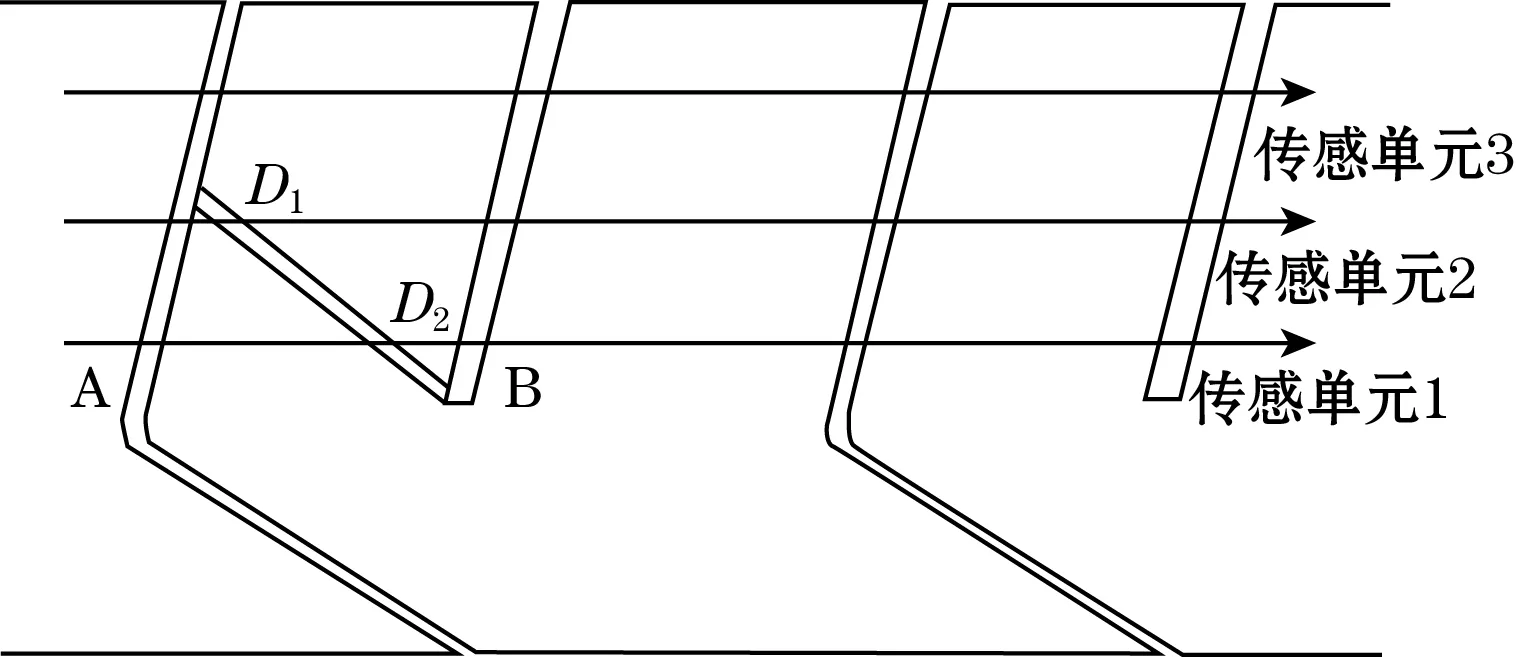
图9 带有裂纹的轮胎胎冠花纹
传感单元1与传感单元2出现了噪声,这是轮胎胎面不平整导致的。此类噪声与裂纹幅值差异大容易区分,滤波后不会影响裂纹的识别。
裂纹与正常花纹有一定的区别,持续时间较短且没有重复性。MATLAB软件编程可以对裂纹的点定位,流程图如图10所示。正常轮胎花纹每个周期的花纹数少,不难判断每个周期花纹间的沟槽数,确定了沟槽数也就确定了周期。D1和D2点为程序最后所得点,如图11所示。由D1和D2的出现时间和幅值平均值可得裂纹深度3.4 mm,真实裂纹深度3.3 mm。单排传感单元的间距为6 mm,长度0~12 mm的裂纹存在漏检问题,为解决此问题,可以将传感器阵列为n排结构交错放置。识别的最短裂纹为6/nmm,并且可以根据检测到裂纹的传感单元数估测裂纹长度。

图10 裂纹检测流程
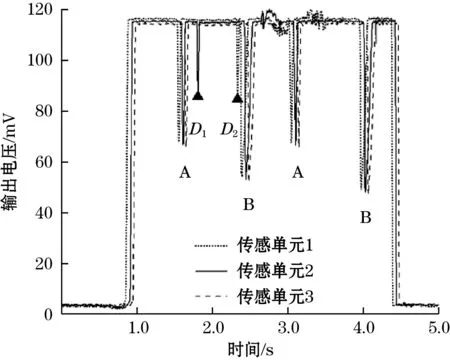
图11 轮胎胎冠裂纹检测
5 结束语
根据动物毛发感知机理结合磁致伸缩逆效应、欧拉-伯努利梁结构力学原理、胡克定律设计了一种用于检测车辆轮胎胎冠裂纹的磁致伸缩触觉传感器,对 Galfenol片长度进行了优化。推导传感单元的输出特性模型,并将传感单元阵列为1×3的结构。搭建了传感器输出特性测试系统,对传感器进行了静态与滑动性能以及各单元间的差异测试。实验结果表明传感器灵敏度高达170.5 mV/N,恢复与响应时间小于80 ms。触觉传感阵列输出的动态信号可以检测胎冠裂纹的位置、深度与估测长度。

