基于GA-ACO-BP网络的机床主轴热误差预测＊

田春苗 季泽平 阿勇嘎 张学炜 唐术锋 郭世杰

（内蒙古工业大学机械工程学院，内蒙古 呼和浩特 010051）

数控机床作为现代加工制造业的基础，其精度对制造业的发展起到至关重要的作用[1-2]。影响机床精度主要因素中几何误差与热误差的占比最大[3-5]。诸多研究表明，热误差是影响机床精度的主要因素之一，其占机床总误差约40%～70%[6-7]，因此减小热误差的影响是提高机床精度的主要途径之一。随着科学技术的飞速发展，机床的制造和设计工艺以及装配精度得到提高，使得其他因素对精度影响大幅降低。同时，高端制造业的发展对机床的精度提出更高的要求，随着机床精度等级的提高，热误差的影响更加突出[8-9]。而主轴是数控机床核心部件，主轴在高速转动时会产生大量热，引起机床零部件热变形，产生加工误差。因此对主轴热误差预测模型的研究具有重要意义。

近几年，国内外学者在机床热特性、热误差建模及补偿方面做了大量研究[10-11]。热误差预测模型的准确性是热误差补偿的基础。针对热误差建模的研究已经成为该领域的研究重点。为此，学者们使用大量方法建立热误差预测模型，其中包括最小二乘法、多元线性回归、灰色系统理论、支持向量机（SVM）、时间序列模型、人工神经网络、卷积神经网络（CNN）和循环神经网络（RNN）等，这些方法均能构建温度与热误差之间的非线性映射关系[12-19]。传统建模方法主要包括多线线性回归、最小二乘法等适用于结构简单精度等级较低的数控机床，但针对复杂结构机床，传统建模方法难以表征温度与热误差之间的复杂关系，这使得机器学习等智能算法成为现今热误差建模的主要方法。SVM模型适合处理小样本数据，但其核函数的选择较为重要，且核函数选择直接影响模型的预测精度，针对此缺点学者提出使用鸡群（CSO）、遗传算法（GA）等智能优化算法对SVM模型进行优化[20-21]。时间序列模型拥有较高的泛化能力，但与其他网络模型相比，预测精度欠佳[22]。循环神经网络进行建模时难以处理长期依赖问题，为此学者使用RNN网络的变种长短记忆神经网络（LSTM）进行建模，深度学习LSTM预测模型拥有更高的预测精度，但网络需要更深层的学习，因此模型需要更长的训练时间[23]。BP神经网络建模是应用最广泛的建模方法之一，但其易陷于局部最优，且网络权值阈值以及隐含层节点数等需要依据经验人为确定，缺乏理论支撑，针对此缺陷学者们使用优化算法来改进BP神经网络，如：GA-BP模型[24]、PSO-BP模型[25]以及ACO-BP[26]模型等。ACO优化算法是Marco Dorigo等人提出的一种用来寻找优化路径的概率型算法[27]。通过模拟蚁群觅食来搜寻全局最优解，蚁群算法采用正反馈机制，具有较强的全局寻优能力。然而与其他优化算法相同蚁群算法在进行全局寻优的同时，网络自身也存在易陷于局部最优和收敛速度慢等缺陷。

针对以上问题，本文提出K-means++算法对温度变量进行聚类分组，并结合Person、Sperman和Kendall3种相关性分析方法确定最佳热敏感点；提出一种融合算法，利用GA算法初始化蚁群信息素并生成新的种群，进而解决蚁群算法收敛速度慢和易陷于局部最优的缺陷，建立基于GA-ACO-BP网络的数控机床主轴热误差预测模型。使用GA-ACOBP网络构建温度变量与主轴热伸长误差、主轴热偏移误差和主轴热倾斜误差间的非线性映射关系。依据实测数据，比较BP模型与GA-ACO-BP模型的预测能力。

1 热误差建模

1.1 基于 K-means++算法的温度测点分组

通过K-means++算法对温度变量进行聚类分组，再利用相关性分析计算每个温度测点与热误差之间的相关系数，确定最佳热敏感点，减小温度测点个数，从而解决温度测点间的多重共线性，以提高热误差预测模型的计算速度及预测精度。设T={T1,T2,···,Tn}，是待进行 K-means++聚类分析的全部温度变量样本，T中每个对象称为样本Ti(i=1, 2, ···,n)。

聚类算法具体流程如下：

（1）确定聚类数K

由于K-means++算法需要人为设置聚类个数K的值，K值直接影响聚类结果准确性，本文采用手肘法计算误差平方和(SSE)，确定最优K值。

式中：p表示集群Ci中的所有点温度数值；m表示每一类的聚类中心。

（2）选择初始聚类中心

从温度数据集中随机选择一个温度测点作为初始聚类中心。

（3）计算温度样本中每个温度数据到初始聚类中心Tu的欧氏距离D，为

式中：j=1, 2, ···,m(m为温度向量中数据样本的个数)；Ti,j表示温度向量Ti中的所有温度数据；Tk,j表示初始聚类中心Tk中的所有温度数据。

（4）增加距离最远温度向量作为下一个聚类中心的概率。

（5）重复步骤（3）和步骤（4），直至选出k个初始聚类中心。

（6）计算温度向量到每个初始聚类中心的欧氏距离。

（7）将每一个温度变量分配到欧氏距离最近的聚类中心的类簇中。得到k个类簇{C1,C2, ···,Ck}，在每一个簇中更新聚类中心。

式中：∣Cl∣表示各簇中温度测点的个数，1≤l≤k；Ti表示各簇中第i个温度测点，1≤l≤∣Cl∣。

（8）重复步骤（6）和步骤（7）直至聚类中心的位置不再发生改变。

1.2 温度测点优化

进行分组后，还需消除温度变量之间的多重共线性。为此，本文在K-means++算法分组后，分别采用person、sperman和kendall这3种相关系数来确定温度变量与热误差之间的相关程度，并在每一簇中选择一个温度测点作为热敏感点。

依据上述K-means++聚类分组结果，计算全部温度变量与热误差之间相关系数：

（1）person相关系数

式中：Ei表示热误差数据。

（2）sperman相关系数

式中：n是数据的数量；rg为数据的秩次。

（3）kendall相关系数

温度变量和热误差变量T与E中包含的数据个数均为N，第i(1≤i≤N)个组合为 (Ti,Ei)，第j(1≤j≤N)组合为 (Tj,Ej)，若Ti＞Tj且Ei＞Ej，或Ti＜Tj且Ei＜Ej出现时，则称第i个组合和第j个组合是一致的；若Ti＞Tj且Ei＜Ej， 或Ti＜Tj且Ei＞Ej出 现时 ，则称两组合不一致。kendall相关系数表达式为

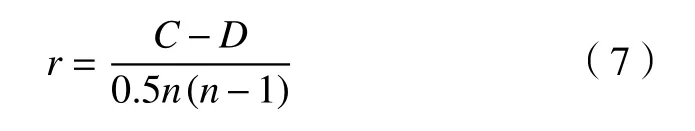
式中：C和D分别表示一致和不一致组合的数量。

通过对温度数据和热误差数据的相关性分析，可确定各聚类分组中的最佳温度测点。将各分组中相关性最大的温度变量作为热误差预测模型的输入，避免了温度变量之间的多重共线性。

1.3 BP 神经网络建模

BP 神经网络是一种多层前馈神经网络，具有极强的非线性映射能力，是目前应用最广泛的神经网络模型之一[28]，具体建模过程如下：

依据Kolmogorov定理，确定BP网络隐含层节点数，最大迭代步数，学习效率。初始化网络权值阈值。

计算隐含层输出

式中：g(x)为激活函数sigmoid；n为输入层节点数；wij为输入层到隐含层的权值；aj为输入层到隐含层的阈值。

计算输出层的输出

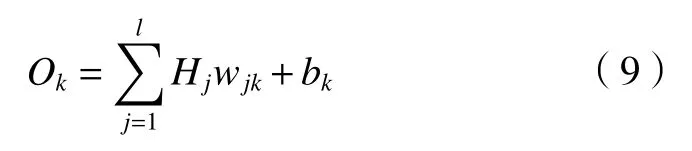
式中：l为隐含层节点数；wjk为隐含层到输出层的权值；bk为隐含层到输出层的阈值。

计算输出误差

式中：m为输出层节点数Yk为期望输出。

更新权重

式中：η为学习速率；ek=Yk-Ok。

更新阈值

1.4 GA-ACO-BP 热误差建模

BP神经网络有较强的非线性映射、自学习和自适应能力，但BP神经网络同样拥有易陷于局部最优解，收敛速度慢等缺点。针对其缺点，构建具有全局寻优能力和高收敛精度的GA-ACO算法，以提升BP神经网络的预测精度。

GA-ACO-BP算法实现的原理是：将蚁群觅食路径赋值为BP神经网络的权值和阈值，通过蚂蚁觅食路线来表征待优化问题的可行解，蚁群中所有个体的觅食路径构成待优化问题的解空间，在较短路径上的蚂蚁所释放的信息素更浓，选择这条路径的蚂蚁也逐渐增多，最终整个蚁群在正反馈的作用下选择此路径，这条路径所对应的解便是最优的权值和阈值。在蚁群进行搜索时，通过遗传算法对信息素浓的蚁群个体进行交叉变异处理，随机生成的蚁群加快了算法的收敛速度，提高了蚁群算法寻优的准确性。基于GA-ACO-BP的热误差建模预测流程图如图1所示。

图1 基于 GA-ACO 优化 BP 网络流程图

基于GA-ACO-BP的热误差预测模型具体步骤如下：

（1）初始化网络。包括BP神经网络输入层到隐含层的权值wij和阈值aj；隐含层到输出层的权值wjk和阈值bk。将全部待优化参数记作p1,p2, ···,pn，针对任意参数，随机选取N个非零值，组成集合Ipi(1≤i≤n)，集合Ipi中元素的信息素为τj(Ipi)(t)=C，(1≤j≤N)，蚁群算法中蚂蚁数量为S，目标函数误差为E。

（2）所有蚂蚁进行搜索，依据概率公式（13）在集合Ipi中随机选择路径，全部蚂蚁完成路径搜索为止。在集合Ipi中，蚂蚁α(α=1, 2, ···,S)任意挑选第j个元素的概率为

（3）构造解空间，更新信息素。从蚁群中随机挑选h个蚂蚁，h=[r·S]，r为动态变化选取率。最优解为信息素浓度最大的蚂蚁个体MAX(τj(Ipi))，蚂蚁i下次迭代行走的路径为

蚁群遍历完所有元素后，使用Ant-Cycle更新集合Ipi中每个元素的信息素，得

式中：ρ为信息素挥发系数；Δβjk(Ipi)为蚂蚁k本次迭代中在集合Ipi中第j个元素路径的信息素[24]。

（4）使用遗传算法对蚁群进行交叉变异操作。随机选择交叉点，对两个染色体进行交叉处理，获得两个新的序列。依据变异概率，随机确定变异个体和变异位置。

（5）依据适应度函数F-FMeasure计算蚂蚁个体适应度，同时还需计算每个个体搜寻路径的时间，若满足最优解条件，转入步骤（6），反之转入步骤（3）。

（6）将GA-ACO算法获取的最优权值阈值输入至BP神经网络，通过公式（9）计算预测误差的差值E。

（7）通过式（11）和式（12）更新BP神经网络的权值和阈值。

（8）若输出结果满足要求，得到最优解算法结束，否则重复过程（2）～（7）。

2 实例分析

2.1 主轴热误差测量

本文以武汉高科机械生产的双转台五轴加工中心GS200-i5-a为研究对象，依据ISO 230-3[29]标准对机床主轴热误差进行测量，并通过五点法辨识出主轴5项热误差，使用电涡流位移传感器测量位移数据，传感器远离检验棒时，位移数据记为正，反之则记为负，传感器布置位置如图2所示。

图2 五点法测量示意示意图

机床关键测点温度数据测量选用高精度磁吸式铂热电阻PT100温度传感器。传感器分布位置如表1所示，主要包括轴承、电机外壳、冷却液进出管、主轴基座以及环境温度。基于红外热成像仪器检测机床主轴温度场，以确定主要热敏感区域。

表1 温度传感器分布位置

其中温度传感器精度等级为A级，量程为-50～100 ℃。电涡流位移传感器量程为2 mm，分辨率为 0.1 μm，工作温度在-30 ～150 ℃。检验棒为φ20 mm×200 mm 的轴承钢。五点法夹具选用 7075铝合金整块切割制成。

为了最大程度符合实际生产加工，分别设计3种不同转速的实验：低速实验、中速实验和高速实验。实验工况设计如表2所示。为避免随机误差的影响，每种工况分别进行3次实验。

表2 试验工况设计

2.2 测试结果与分析

以高速实验中的一组试验结果为例，温度和位移数据的检测结果如图3～4所示。

由图3可知，在主轴运行53 min时，冷却液管处温度传感器数值突然下降，此时机床自动冷却系统开始运行。在运行至200 min时达到热平衡，温度变化趋于平稳。

图3 温度变化曲线

由图4可知，热效应引起的位移量在300 min以后趋于平稳状态，相比温度场达到稳态时间稍有滞后。位移量变化曲线呈现为先增大再减小最后趋于平稳的趋势，位移量最大值出现在200 min，刚好此时达到热稳态，稳态和非稳态状态下传热效率和接触热阻不同，导致位移量在温度达到热稳态后出现一段下降趋势，而后在趋于平衡。

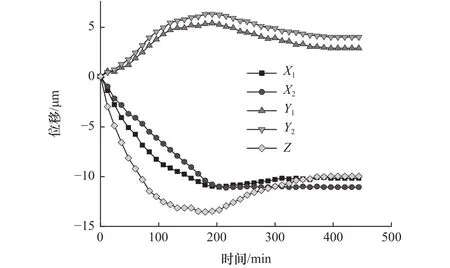
图4 主轴热位移曲线

3 测点优化及模型预测评价

3.1 温度测点优化

T={T1,T2, ···,Tn}，是待进行 K-means++聚类分析的全部温度测点，其中n=10，聚类分组数由手肘法确定，SSE变化曲线如图5所示，最大拐点出现在K=4处，因此最佳组数为4组。依据1.1小节聚类方法，将全部温度测点分成(T1、T4、T6)、(T2、T3、T5)、(T7、T8、T9)和 (T10)这 4 组。计算全部温度测点的相关系数，将各簇中相关系数最大的温度测点作为最佳热敏感点，各测点相关系数如表3所示。

表3 温度测点相关系数

图5 SSE 变化曲线

3.2 模型预测与评价

以图3所示的数据作为训练样本，基于BP神经网络和GA-ACO-BP神经网络对主轴热伸长误差、X向热偏移误差、Y向热偏移误差、X向热倾斜误差和Y向热倾斜误差五项热误差进行预测对比，如图6所示，各模型预测残差如图7所示。

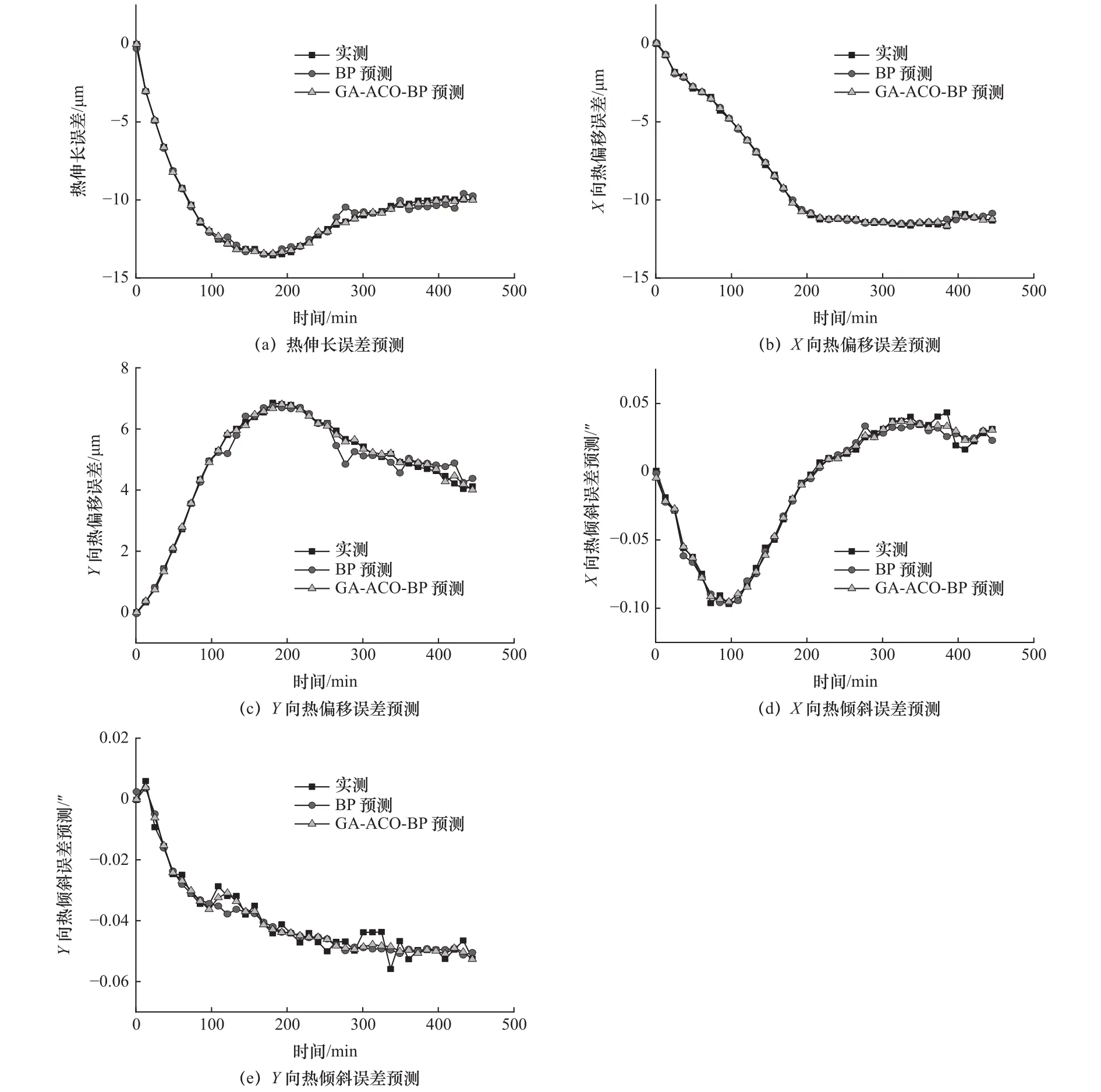
图6 主轴热误差预测

图7 预测残差

以平均绝对误差MAE、均方根误差RMSE、平均绝对百分比误差MAPE评价模型拟合优度。拟合优度参数如表4、表5所示。

表4 BP神经网络拟合优度

表5 GA-ACO-BP神经网络拟合优度

由图6和图7可知，GA-ACO-BP模型预测效果明显优于BP模型。经过平均绝对误差MAE、均方根误差RMSE、平均绝对百分比误差MAPE和残差均值的对比，可以看出，本文提出的基于GAACO-BP神经网络的数控机床主轴热误差预测模型具有更好的拟合优度和更高的预测精度。

4 误差实时补偿过程

将3.1小节中优化后的温度热敏感点作为误差补偿时的温度采集点，通过PC端接受温度数据，传输至已建立好的预测模型中，由计算机实时计算补偿值，计算机通过以太网与数控系统进行实时通讯。同时在机床PLC中配置相应个数的热误差补偿模块“TESPSEM”，如图8所示。

图8 PLC 中“TESPSEM”热误差补偿模块[30]

PLC中热误差补偿模块“TESPSEM”4组参数的说明如表6所示。

表6 “TESPSEM”模块参数[30]

在进行补偿前还需结合温度传感器采集温度数据在数控系统中对各项补偿参数进行设置。热误差补偿是在插补周期内进行的，即插补后补偿。通过监控程序来限制补偿值大小，以免机床过载，再将其与插补输出指令位置进行叠加[31]。补偿的流程图如图9所示。

图9 热误差补偿控制流程图[31]

5 结语

本文提出了基于GA-ACO-BP网络的主轴热误差预测模型，有效地解决了BP神经网络收敛速度慢、易陷于局部最优、预测精度低等缺陷。结果表明：K-means++算法与person、sperman和kendall分析相结合可有效发掘主轴温度变量和热误差之间的相关性，降低了温度测点间的多重共线性。基于GA算法初始化蚁群信息素，并通过交叉和随机变异生成新的蚁群，解决了ACO算法的缺陷，改进后的ACO算法有效优化了BP网络的权值和阈值，提高了热误差预测模型的精度和泛化能力。实验对比结果显示，GA-ACO-BP预测模型更适合确定主轴热误差的补偿值。

热误差的精准预测是实施补偿的前提，本文主要关注的研究内容为主轴热误差的预测，后续的研究中，将在数控机床上进行实时误差补偿，进一步验证该模型的可行性和鲁棒性是下一步研究的工作重点。