航空涡轮叶片扩散型气膜孔电火花铣削加工关键工艺研究＊

王浩杰 曹自洋 张洋精

（苏州科技大学机械工程学院，江苏 苏州 215009）

随着航空涡扇发动机效率不断提升的需求，提高热端涡轮叶片进口温度是重要途径，下一代发动机的热端涡轮进口温度预计将达到 2 300～2 400 K[1-2]，该温度已经超出涡轮叶片高温材料钛/镍基合金可承受温度极限。因此，有效的冷却防护措施可避免其受高温腐蚀和损伤。现代热端涡轮叶片主要采用TBC涂层技术以及气膜冷却技术来解决上述问题，如图1所示。其中先进的气膜冷却技术可起作用约占比60%～70%[3]。通过在涡轮叶片上规律性的分布大量气膜冷却孔，使低温气流从气膜孔中高速通过并在叶片表面沿着高温气流的方向形成冷却薄膜，从而达到气膜降温和隔热，提升叶片在高温环境下工作的可靠性和稳定性[4]。

图1 涡轮叶片主要技术

在现有气膜冷却技术中，在相同的冷气入口压力下，扩散形气膜孔比圆锥形气膜孔以及单纯的圆柱形气膜孔在冷却效率和热传导系数上有明显的优势。扩散型气膜孔由圆柱形孔和扩散形孔组合而成，如图2所示[5-6]。

图2 扩散型气膜孔

据统计，通常在电火花制造过程中，成型电极的制作时间与费用可达总制造周期与费用的一半以上[7]。同时电火花成型加工技术在扩散形气膜孔加工中需要根据扩散孔型反向制作成型电极，制作和更换成本高、小放电间隙中工作液冲液及排屑效果较差以及针对同排不同角度扩散型孔无法采用树状成型加工导致的效率低等问题，电液束加工技术在扩散形孔加工中存在效率低、形孔轮廓度不可控等问题[8]。

电火花铣削加工是电火花加工的一个重要分支，使用简单电极模仿传统机械铣削加工，通过工具电极和工件之间的火花放电，蚀除材料，对工件进行创成加工[9]。同时，电火花铣削加工无需制作复杂的成型电极，而通过使用简单圆柱微细电极，借助数控编程技术，根据型腔三维结构设计合理的分层铣削轨迹[10]，利用电极端部通过水平移动逐层去除工件材料，具有很高的加工效率和灵活性[11-12]。

然而在电火花分层铣削加工中，分层厚度的控制以及转角加工过程中的伺服加减速控制分别影响扩散型气膜孔的纵横截面的轮廓度。

1 分层厚度控制对扩散型孔纵截面轮廓度影响研究

1.1 电火花铣削加工底面轮廓数学模型

在电火花放电加工中的工具电极损耗一般都是相对工件电极而言的，常用相对质量、体积损耗比来衡量，本文为便于分析计算，采用体积损耗比θ=VElectrod/ VWorkpiece。

为分析电火花铣削加工过程中电极损耗和工件损耗的规律，以上述一般自由工件表面为研究对象，采用数学方程的方法进行描述，如图3所示。

图3 电火花加工底面轮廓图

工具电极沿着轨迹y=E(x)放电铣削加工未加工表面y=W(x)，由于存在电极损耗，最终形成已加工表面y=Y(x)，为便于方程描述，y=E(x)已将放电间隙包含在内。

抽取微小距离Δx进行分析，根据损耗关系建立微分方程，并通过积分方程进行求解。

设电极沿X向移动Δx距离，工件去除ΔVW，在加工条件（放电参数、电极材料、电极尺寸和工件材料）不变的条件下，电极体积损耗ΔVE/ΔVW。

电极的体积损耗计算为

式中：SE为电极横截面积； Δl为电极轴向损耗长度。

工件的体积损耗计算为

式中：SW为加工槽的截面积，由于SW是一个变量，由W(x)和E(x)共同租用，为简化分析，设电极加工的槽的截面为矩形，面积计算为

式中：w为槽宽。

整理式（1）～（3）可得

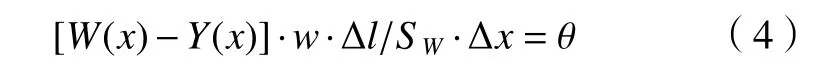
为建立微分方程，将 Δl表达成有关Δx的方程，电火花加工底面轮廓数学模型如图4。

图4 电火花加工底面轮廓数学模型

最终整理为

化简得

对公式（6）、（7）稍作整理得

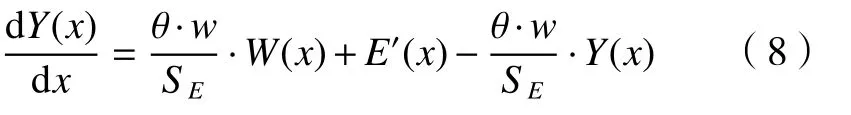
上式为标准的非齐次一阶线性微分方程，其通解为

简化上式，将自由曲面y=W(x)简化为水平平面W(x)=0，将电极运动轨迹方程简化为水平移动，则E’(x)=0，则上式可以简化为

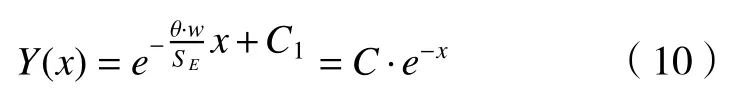
当x=0时，即为槽深，设为-h，则上式为

则工件的轮廓曲线如图5所示。

图5 补偿为 0 的底面轮廓

从加工表面方程和对应的曲线可以看出，如果在加工中不对电极的轴向损耗进行轴向的补偿，则加工出的工件表面随电极的进给逐渐变浅，直到间隙无法被击穿停止放电，此时的槽深为0。

因此，当电极移动距离L损耗Δle时对其进行轴向补偿，补偿量为Δle。即

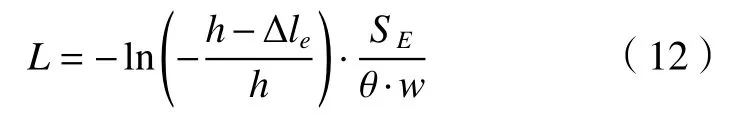
因此，每当电极移动距离L时进行补偿（如图6），当移动到第n倍L时，工件底部轮廓方程为

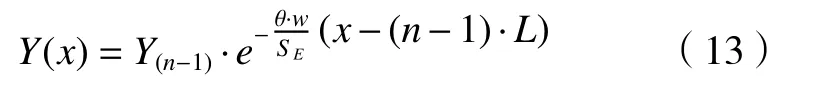
图6 电极补偿示意图

根据上述方程（1）～（13）利用MATLAB进行仿真计算。在仿真之前，设计单槽加工工艺试验获取仿真所需要的电极直径、加工槽宽、损耗比数值。试验条件如下：

试验采用ZNC-540电火花小孔机床，工件为718高温合金，工具电极采用外径0.6 mm，内径0.25 mm的紫阳铜电极，试验的电参数如表1所示。

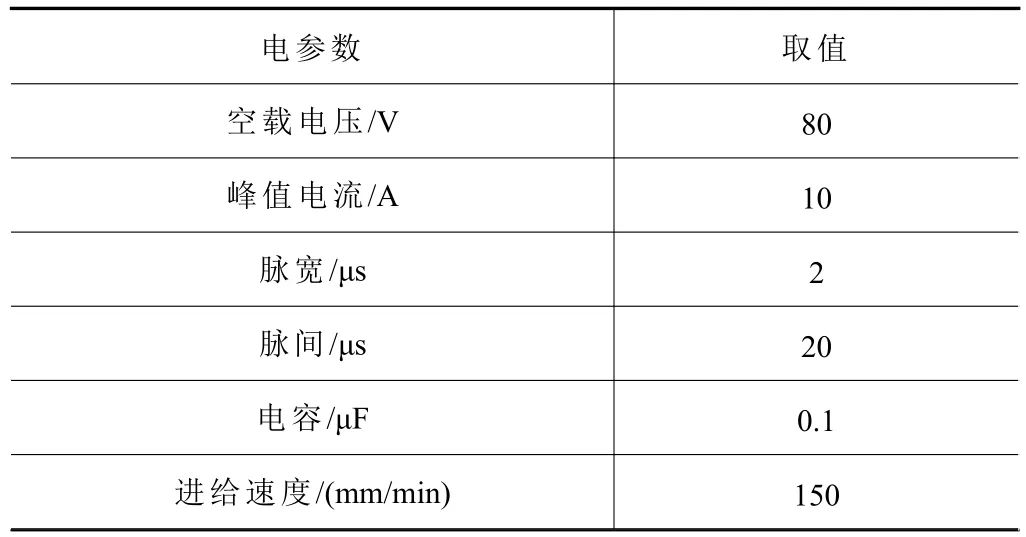
表1 损耗比试验参数表

在上述试验条件下，采用往复电火花铣槽的方式进行损耗比和槽宽测试，槽长10 mm，每层设置加工层厚0.005 mm，往复铣削100次。经过多次试验测试，损耗比为25.6%。

1.2 MATLAB 仿真模拟

根据上述试验结果，在MATLAB中进行仿真计算，设电极直径为600 μm，机床最小补偿精度Δle=1 μm，加工层厚 5 μm，电极损耗比θ=25.6%。当初始分层厚度小于或者大于5 μm时，仿真结果如图7。

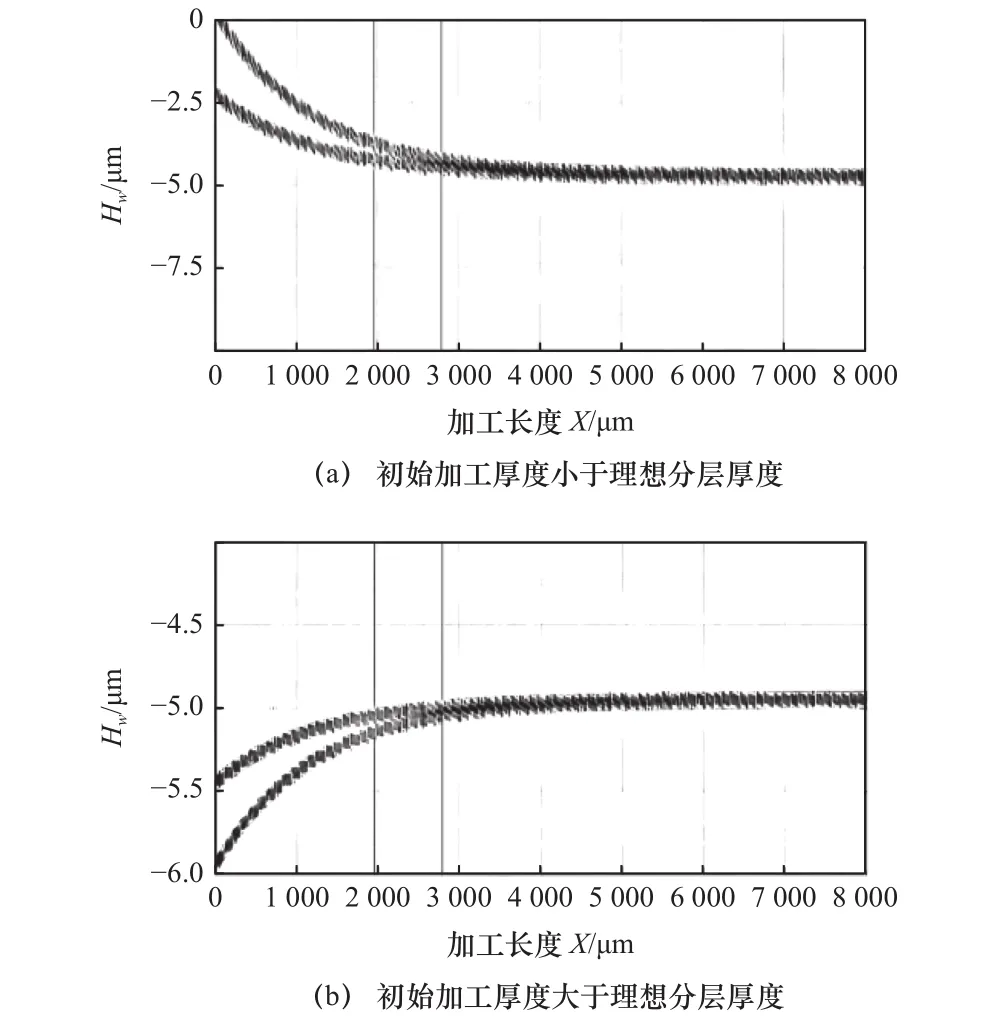
图7 不同初始加工深度底面轮廓图

从图7可以看出，当初始加工深度与理想分层厚度有偏差时，加工的深度只对初始的一小段距离会产生影响，且会逐渐逼近理想分层厚度。其原因可以通过图8进行分析，为简化分析过程，象征性地取前3层进行分析。

图8 初始加工深度对底面轮廓分析过程图

从图8可知，首层加工结束后进行层间进给并开始加工第二层，第二层开始加工时的放电间隙较第一层变小，间隙放电能量加强，因此第二层的加工深度较第一层变深，同理分析第三层，直到加工深度逼近理论深度。

1.3 试验

为验证仿真计算结果，设计如下试验。在实际的加工中，影响初始加工深度的因素主要有放电能量、初始放电间隙等，本次试验选择不同放电能量参数来分析初始层厚对加工实际轮廓的影响，试验参数如表2所示。

表2 初始加工深度试验参数表

取扩散型孔的纵向截面来描述加工过程，如图9所示，电极通过逐层扫描的方式进行加工，当第i层加工完后，电极进给到下一层继续加工，将电极从第0层到最后一层的加工轨迹按照直线展开，类似于加工一长直线。

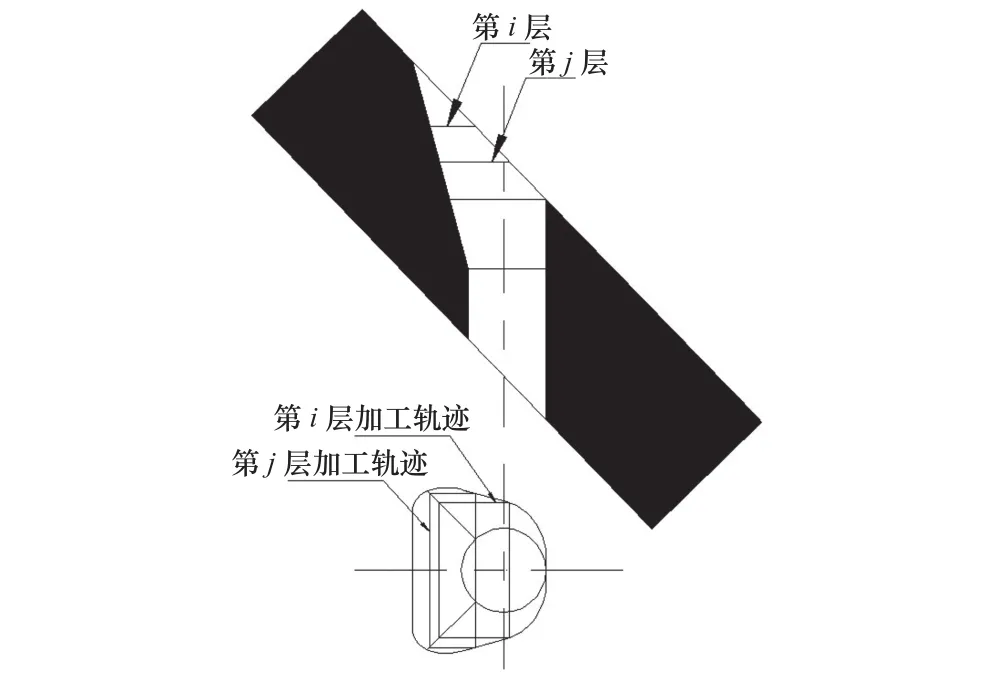
图9 扩散型孔逐层加工示意图

根据表2的试验，结果如图10所示。

从图10可以看出，试验参数1所采取的放电能量小于稳定值，即所加工的初始深度小于设定5 μm，导致初始段加工深度较浅，而随后逐渐趋于稳定，试验参数2的能量强于参数1而弱于稳定参数，因此其初始段加工深度大于试验参数1而小于稳定参数。最终稳定参数加工结果经检测纵截面表面轮廓度即平面度为 0.008 3 mm。

图10 扩散型孔试验加工结果

2 转角伺服加减速对扩散型孔横截面轮廓度影响研究

2.1 电火花横向扫描加工简析

电火花铣削加工三维结构是采用简单的中空圆柱形电极，按照一定的加工层厚逐层切片式扫描加工，电火花端部放电切片式扫描加工示意图如图11所示，圆柱电极首先沿轴向进给至工件表面，然后以Vx横向移动，同时，根据事先测试好的电极/工件损耗比，电极在横向移动的同时，按照一定的速度Vz轴向向下进给以保持稳定的放电间隙来进行持续的放电加工。

图11 扫描加工示意图

在电火花伺服扫描加工每一层时，检测电路实时检测电极端面的电压电流信号，以判别3种放电状态：开路、火花放电以及短路。

当电火花的放电能量和其他预定的加工条件一定时，横向扫描的加工速度直接影响当层的加工深度，而影响横向扫描加工速度的主要影响因素有两个：一是电极向下进给的速度Vz，Vz控制主要由电极的损耗补偿值是否精确来保证；二是机床的伺服加减速特性，尤其在转角处加工时尤为明显。

从图9可以看出，扩散型孔的横截面加工轨迹为矩形，每层有4个弯。本文主要研究转角处的伺服加减速特性对扩散型孔横向截面轮廓度的影响。

2.2 横向扫描速度对加工深度的影响

当电极横向扫描速度愈慢，在该处加工时间愈长，加工深度就会愈大，极端情况下，如果横向扫描速度为零，则就转化为钻孔加工；如果横向扫描速度过快，每层加工深度过浅，可能形成不完全加工的结果，横向扫描速度对加工深度的影响如图12所示。

图12 扩散型孔试验加工结果

而影响电极扫描速度最敏感的部位为电极移动方向发生变化，尤其是90°转角，因在转角处，机床各轴的伺服运动会存在不可避免的加减速问题。

对比扫描速度和加工深度的图，当扫描速度等于0时，铣削加工将转化为钻孔，导致该位置处深度加大。而从扫描示意图可以看出，如果在90°转角处，运动轴的伺服加减速控制测量将速度降为0将导致各转角处的深度明显加深，从而影响零件的轮廓度。

因此，需要对90°转角处的加减速和路径进行重点规划设计。

2.3 横向进给速率即转角误差控制

在数控机床加工过程中，伺服电机按照根据编程控制运动轴按照规划的插补和加减速进行运动，其中加减速运动控制主要用来避免各轴不连续的进给率，从而保护机床并保证可靠的精度。

对于直线段来说，常采用S型速率控制曲线，如图13。图13分为3段式：第一段为加速段，包含区域（1）～（3）；第二段为匀速段，即区域（4）；第三段与第一段相反，为减速段，包含区域（5）～（7）。在数控加工中，若采用S型加减速控制策略，在起始和结束时机床会产生明显的振动，影响加工的稳定性。尤其在两段直线呈90°时，会产生更加明显的振动，对于航空涡轮微小扩散型气膜孔的加工精度影响更大，气膜孔的三维尺寸精度无法保证。为此，本文对带较大夹角的两段直线加工，重新规划加减速策略，使过程中速率的变化更加顺滑。

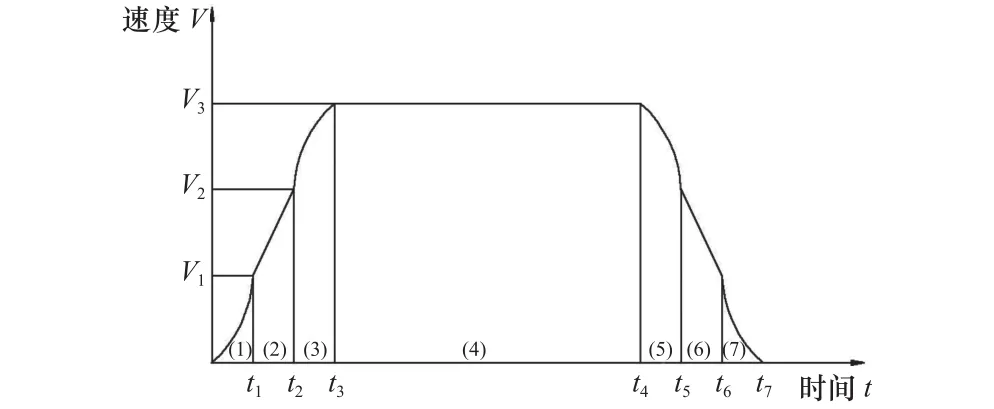
图13 S 型加减速控制曲线

针对图13中S型加减速各段控制的数学方程如下。

式中：V为速率；t为时间；Jmax为最大波动值；aset为自定义加速度。

在数控控制中，顺滑的加工路径和进给率规划是制定合理混合进给率和低转角误差的基础。本文以呈任意角度θ的两直线为例进行误差分析说明，如图14。

图14 带夹角路径误差示意图

根据三角函数关系可以得出最大允许误差emax和终端误差e以及θ之间的关系：

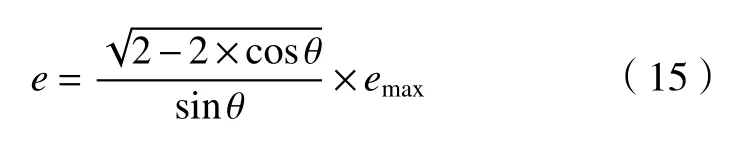
因此，可以用两直线之间的夹角θ和允许误差e来规划转角速率。

针对上述两夹角误差示意图中的P1P2段和P2P3段进行分析。从S型速率控制曲线图中可以看出，减速区有（5）～（7）共3个区域，根据P2P3段和P1P2段不同的连接位置，确定不同的混合进给速率规划，如图15所示。

图15 两段S型伺服进给混合控制示意图

针对图15a，即区域（5）分析，多项式如下。

式中：

针对图15b，即区域（6）分析，多项式如下。

式中： β =V1+V2+asett5。

针对图15c，即区域（7）分析，多项式如下。

式中：

在试验编程时，根据零件的图纸三维轮廓精度要求，对emax，加减速时间，以及P1P2路径的进给速度V1，程序将根据上述多项式自动求解处转角进给速度V，以及在夹角θ到混合进给率曲线规划之间的时间t。

2.4 试验

为验证算法的有效性，采用实际的试验测试验证，试验条件如表3所示，不同转角伺服控制策略的试验结果如图16所示。

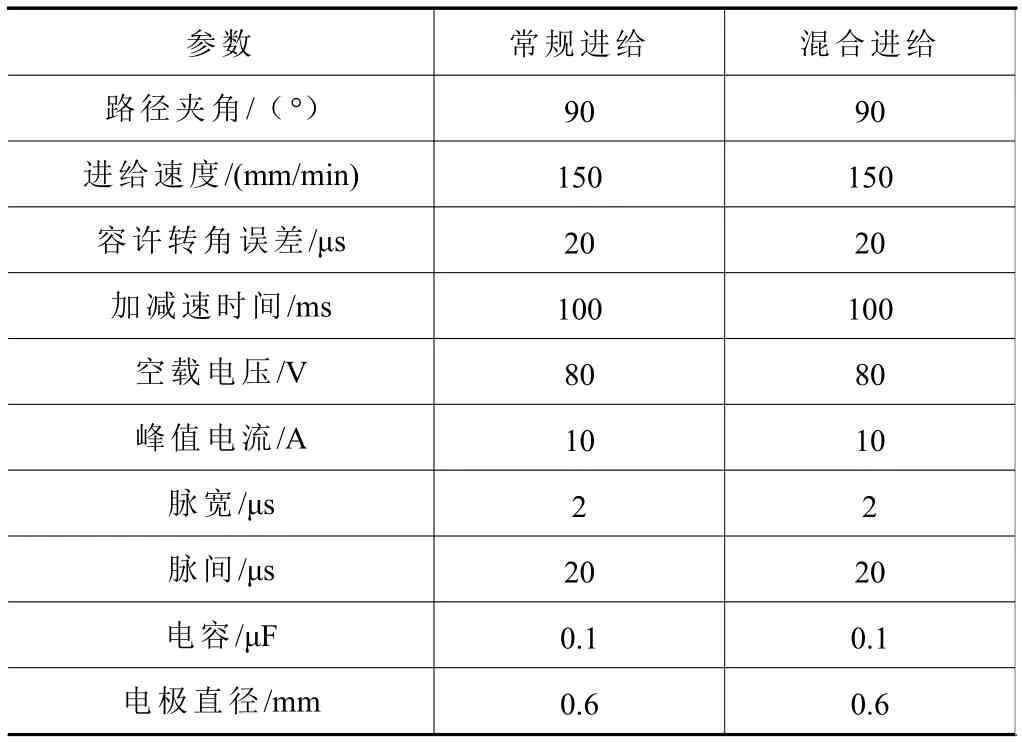
表3 不同转角伺服进给控制试验参数表

从扩散型孔横截面图16可以看出，当转角处采用混合转角伺服进给控制时，90°转角处因没有多大的速度下降，转角处停留的时间较短，不会造成明显的内凹现象。

图16 不同转角伺服进给控制试验扩散型孔横截面图

3 结语

针对航空涡轮叶片扩散型气膜孔加工，国内普遍采用传统电火花成型工艺和电液束工艺加工，而对电火花铣削加工工艺的研究较少。同时关于电火花铣削加工技术的研究主要集中在电极等损耗补偿、电参数对加工表面粗糙度以及重铸层厚度的影响等方面，缺乏对加工中影响气膜孔轮廓度的研究，本文创新点在于针对铣削加工中分层厚度、运动轴90°转角伺服加减速控制等关键工艺进行理论与实验探究，分析其对三维结构纵横截面轮廓度的影响，提高加工精度，得到以下结论：

（1）针对扩散型气膜孔纵截面，在合适的体积损耗比下，当初始加工深度大于或小于理想分层厚度时，其仅对初始阶段一小段长度内的加工深度有影响，随后在理论加工层厚附近趋于稳定。为获得精度较高的扩散型气膜孔纵截面轮廓度，需要设置合理的放电参数、初始放电间隙等控制初始加工深度。

（2）针对扩散型气膜孔横截面，采用混合S型伺服进给控制策略，对铣削加工各层横向截面90°转角处的深度控制精度较高，能够有效降低常规转角伺服控制引起的内凹截面。