叶片稠度对压气机最大有效静压升影响的数值模拟

2022-08-30 09:18王同辉王志强王学高

南京航空航天大学学报 2022年4期

王同辉，王志强，王学高

（南京航空航天大学能源与动力学院，南京 210016）

压气机的长度、重量在整台发动机中占比很大，生产、维护费用高昂，并且研发难度大，技术含量高，其性能对整台发动机的性能有决定性的影响。因此，压气机是航空发动机最关键的部件之一，其性能优劣直接影响整机的研制［1］。

压气机的不稳定工作状态主要有旋转失速和喘振两种。旋转失速和喘振现象是叶轮机械中最严重的气动问题。对航空燃气涡轮发动机而言，进入旋转失速和喘振状态不仅会对压气机耐久性造成影响，而且会引起性能降低，严重时甚至导致发动机熄火。因此在发动机实际运行过程中要确保压气机不能进入旋转失速和喘振状态。因而在压气机的设计过程中，需要一种可靠的方法来评估一台新压气机的稳定裕度，压气机的稳定边界预测问题显得十分重要［2］。正因为如此，迄今为止，压气机稳定边界预测方法仍然作为外国公司的核心商业机密不予公布。

多年来，随着人们对压气机内部流动不断深入研究，主要得到了3 类关于压气机稳定性的分析方法。第一类是经验关联法。在研究压气机稳定性的早期，科研工作者对大量的实验数据进行总结分析和研究，将多个设计参数和工作参数关联起来，建立起判断压气机稳定性的准则参数，以此作为压气机失稳的判断标准。在这一阶段，Emmons等［3-9］提出了多种评估压气机稳定边界的经验准则，其中具有代表性的有：Dunham［7］提出将压气机压升系数和流量系数关联曲线上导数为零的点作为压气机的失稳边界点；Leiblein 等［8］提出将扩散因子作为压气机稳定性判断的近似准则；Koch［9］提出用最大静压升系数来评估压气机的最大压升潜力。在这类方法中，Koch 提出的最大静压升系数法最具代表性，其关联的影响因素最为全面。第二类方法以小扰动的线性稳定性理论为主，用于预测风扇/压气机或压缩系统的工作稳定性［10-11］。第三类方法不仅关心风扇/压气机或压缩系统在平衡工作点受小扰动的稳定性，还非常重视有限扰动对稳定性的影响及其发展情况，以及压气机失速后两类失速流态——旋转失速和喘振的性质，这类方法为建立在时域上的时间推进法［12-18］。

20 世纪80 年代，Koch 提出了采用最大失速静压升判断压气机气动稳定性的方法［9］，该方法属于经验关联法，这类型的方法依据实验数据，使用经验关系式来判断压气机状态点是否失稳，因此有一定的误差，但是其优点是使用简单、便捷。相对于另外两种方法，其优势为：（1）在压气机设计阶段，已知压气机设计参数时，就可以使用该判据进行稳定性判别；（2）该判据适用性较广，可以用于其他气动计算程序中。

上述3 类压气机稳定性分析方法均存在不足之处，但有文献表明，Koch 最大有效静压升系数法经过不断发展之后，至今仍然被GE 公司使用，此前，已有一些关于最大有效静压升的应用［19-23］，但是文献［9］公布的最大有效静压升的预测曲线是否准确，国内尚无人开展过系统的验证，并且国内对于设计参数对压气机有效静压升影响的研究甚少，对该方法的有效性和适用性也没有开展系统的研究。

为探究相关设计参数对压气机最大有效静压升的影响，本文针对某单级低速压气机，通过改变转静子叶片数，构建了不同叶片稠度的压气机模型，采用三维数值模拟的方法，研究了叶片稠度的改变对压气机最大有效静压升系数的影响。

1 研究对象

本文的研究对象为课题组设计的一台等内外径的单级轴流压气机，负荷系数为0.35，静子叶片的固定形式为悬臂式，该压气机的设计参数如表1所示，其中，转静子的设计参数值用斜杠隔开。由于仅研究轴向均匀进气情况，各工况的流场均可近似认为轴对称分布，叶栅各通道流动状况相似，为了节省计算资源和计算时间，本文针对不同计算模型，均开展了单通道的数值模拟。计算模型的3D视图如图1 所示。

表1 压气机设计参数Table 1 Compressor design parameters

图1 计算模型Fig.1 Computational model

2 数值模拟方法

本文的数值模拟计算采用NUMECA FINE/Turbo 软件包，计算类型为定常，求解流动方程为雷诺平均的 N-S 方程，湍流模型使用Spalart-Allmaras（S-A）一方程模型。网格划分采用O4H 网格，即叶片周围采用O 网格，主流区及进出口区域采用H 网格。对上述计算模型进行了网格无关性验证，最后确定的满足计算要求的网格数为305 万个，第一层网格厚度为0.006 mm。计算结果显示壁面处的Y+都在10 以内，说明第一层网格的厚度满足S-A 湍流模型的计算要求。

为了研究叶片稠度对压气机最大有效静压升的影响，针对上述单级低速压气机，通过改变转静子叶片数，构建了不同叶片稠度的压气机模型，稠度变化方案如表2 所示。表中，R36-S39（ori）表示基准型压气机，其转子叶片数为36，静子叶片数为39，R33-S36 表示此压气机的转子叶片数为33，静子叶片数为36，其余与之类似，表中还给出了不同叶片数情况下，压气机转静子叶片的稠度和无量纲扩散长度L/g2。

表2 压气机转静子叶片数改变方案Table 2 Scheme of changing the number of compressor stator blades

3 最大静压升系数法

Koch 基于大量低速轴流压气机和部分高速风扇/压气机实验数据的支持，将风扇/压气机叶栅通道类比于二维扩压器，提出了最大静压升系数的概念来评估压气机的压升潜力，得到了压气机失速时的最大有效静压升系数Ch，ef与无量纲扩散长度L/g2的关联曲线，如图2 所示［9］。利用该关联曲线即可在压气机的设计阶段，根据各级的无量纲扩散长度预估出各级的最大有效静压升系数，从而预测出整台压气机的稳定边界，为压气机的设计提供了极大的便利。

图2 最大有效静压升系数预测曲线[9]Fig.2 Prediction curve of maximum effective static pressure rise coefficient[9]

本文采用数值模拟的手段对该方法展开研究，下面将对该方法进行简单介绍。压气机各排的无量纲扩散长度的计算为式中：Cp为气体的定压比热容，γ为绝热指数，T1为级进口面平均静温，p1和p2分别为级进出口截面的静压值（本文计算时分别取为进出口截面流量平均的静压值，进口截面取距转子前缘20 mm 处，出口截面取距静子尾缘20 mm 处），U为牵连速度，对于平直流道，U1=U2。

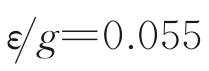
图3 雷诺数修正系数[9]Fig.3 Reynolds number correction factor[9]

图4 叶尖间隙修正系数[9]Fig.4 Tip clearance correction factor[9]

图5 轴向间隙修正系数[9]Fig.5 Axial gap correction factor[9]

式中：S为中径处的栅距，ξ为中径处的安装角（与轴向夹角）。

同时还要考虑速度三角形的影响，用级平均的有效动压头修正系数Fef，Stage（有效动压头修正系数为有效动压头和自由流动压头的比值，具体公式见文献［9］）对静压升系数进行修正，最终，压气机的有效静压升系数为

4 计算结果及分析

本文对转静子叶片数不同的各压气机进行相同边界条件下的数值模拟，计算通过逐渐增大背压使压气机由堵塞工况（大流量）向失速工况（小流量）推进，取数值计算最后一个稳定收敛的解作为稳定边界工况点。对各压气机的计算结果进行对比，分析叶片稠度对压气机性能和最大失速静压升的影响。

图6 为稠度不同的各压气机特性对比图，其中图6（a）为效率特性，图6（b）为压比特性。对比图中转子叶片数相同，静子叶片数不同的3 组曲线可以发现，随着静子叶片数的增加，压气机大流量工况的效率和压比均有所下降，而小流量工况的压比和效率基本没有变化，此外，随着静子叶片数的增加，压气机失速点流量呈逐渐减小的趋势，说明静子稠度的增加达到了扩大压气机稳定工作范围的效果。这是因为在大流量状态下，压气机内部的流动状态相对较好，没有出现明显的流动分离现象。静子叶片稠度的增加，增大了气流与叶片之间的摩擦面积，导致摩擦损失增大，从而导致大流量状态下压气机的压比和效率都随稠度的增加而减小。而在小流量状态下，由于来流迎角的增加，逆压力梯度也随之增大，静子通道内会出现附面层分离现象。此时静子稠度的增加，虽然也增加了摩擦损失，但同时也增加了静子通道内的扩压长度，减小了逆压力梯度，达到了抑制附面层分离、减小流动损失的效果。综合来看，在小流量状态下，静子稠度的增加对压气机效率和压比的影响较小。此外，由于静子稠度的增加，具有抑制附面层分离的效果，从而使得压气机能工作在更高的背压下，即扩大了压气机的稳定工作范围。

进一步对比图6 中静子叶片数相同、转子叶片数不同的3 组曲线可以发现，随着转子叶片数的增加，压气机大流量工况的效率和压比均有所下降，而小流量工况的压比和效率却是增加的。这说明与静子叶片数增加带来的影响相同，转子叶片数的增加，在大流量工况下，增大了摩擦损失，但在小流量工况下，可以达到抑制流动分离，改善压气机内部流动的效果，使得压气机效率和总压比得到提升。通过对比还可以发现，静子叶片数相同时，随着转子叶片数的增大，压气机的稳定工作范围基本不变，稳定边界点流量变化不明显，但其稳定边界点的效率和压比都随着转子叶片数的增加而增大，压气机近失速点压升能力增强。

图6 叶片数不同时压气机的效率和压比特性对比图Fig.6 Comparison diagram of compressor efficiency and pressure ratio characteristics when the number of blades is different

综合转静子叶片稠度变化对压气机性能的影响可以看出，在不同工况下，转静子叶片稠度的变化对压气机性能的影响是相同的，在大流量工况下，稠度增大会增大摩擦损失，降低压气机性能，而在小流量工况下，稠度的增加，可以起到抑制流动分离，减小流动损失，提高压气机性能的作用。另外，针对本文研究的这组压气机而言，流动失稳可能起始于静子通道，所以静子稠度的增加可以扩大压气机的稳定工作范围，而转子稠度的增加并没有与之类似的效果。

为了进一步验证上文的分析，给出了静子叶片数不同的压气机模型在近失速工况下的流场分布，图7 为静子叶片通道内不同轴向截面处的相对马赫数云图。从图中可以看出，静子叶片通道内的流动分离主要集中在两个区域，一个是叶根区域由径向间隙处泄漏流引起的泄漏涡，另一个是顶部附近的叶片附面层分离。对不同压气机的马赫数云图进行对比，可以发现，静子叶片数变化时，马赫数云图变化很小。随着静子叶片数的增加，静子叶片通道内的分离涡略有减小，这是因为随着静子叶片数的增加，叶片对气流的约束略有增强，从而抑制了流动分离，减小了流动损失。结合上文压气机特性线分析，在近失速区，静子叶片数的增加一方面使得摩擦损失增大，另一方面又能够抑制流动分离，所以近失速区压气机的效率和压比基本不变。此外，从特性变化可以看出，静子叶片数的增加，可以使得压气机失速点流量减小。图7 中对比的各压气机虽然都是在近失速工况下，但各压气机的工作流量是不同的。静子叶片数最多的压气机其近失速点工作流量最小、负荷最大，但其静子叶片通道内的流场结构与其他压气机相比没有恶化，这也从一个侧面说明，静子叶片数的增加可以更好地控制静叶内部的流动分离，提高压气机的扩压能力。

图7 静子叶片数不同时近失速点相对马赫数分布Fig.7 Relative Mach number distribution near stall point when the number of stator blades is different

图8 为转子叶片数不同的压气机模型在近失速工况下，转子叶片通道10%叶高S1 流面熵云图。从图中可以看出，转子叶片吸力面尾缘的高熵区非常明显，这说明转子叶片吸力面尾缘发生了较严重的气流分离，造成了很大的流动损失。对比可以发现，随着转子叶片数的增加，转子叶片尾缘高熵区范围逐渐变小，且熵增也逐渐减小，这说明叶片数的增多有利于气流组织，可以抑制附面层分离，改善压气机内部流场，减小流动损失。结合上文压气机特性线分析，在近失速区转子叶片数的增加虽然使得摩擦损失增大，但同时抑制了流动分离，所以近失速区压气机的效率和压比反而增大了，相应的扩压能力也得到了提高。

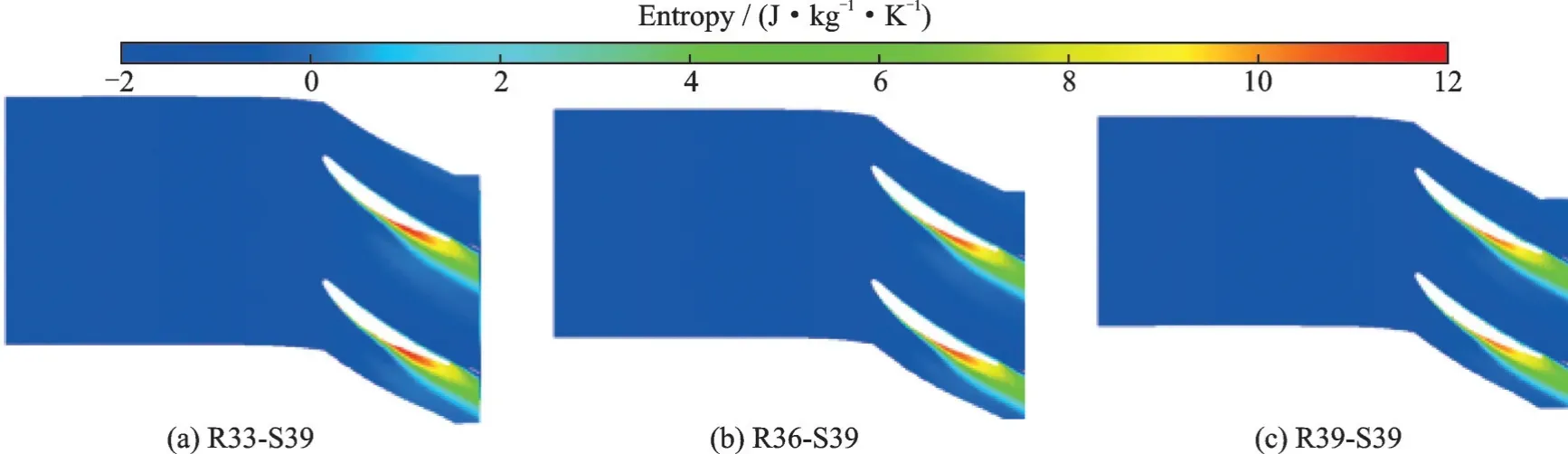
图8 转子叶片数不同时近失速点10%叶高S1 流面熵分布Fig.8 Entropy distribution of S1 flow surface at 10% blade height near stall point when the number of rotor blades is different

图9 为叶片数不同时压气机的静压升系数随流量变化曲线。从图中可以看出，叶片数不同时，压气机的静压升系数均随着流量的减小而增大，静压升系数在稳定边界工况点达到最大值，这说明将最大静压升系数作为预测压气机稳定边界的判据是可行的。

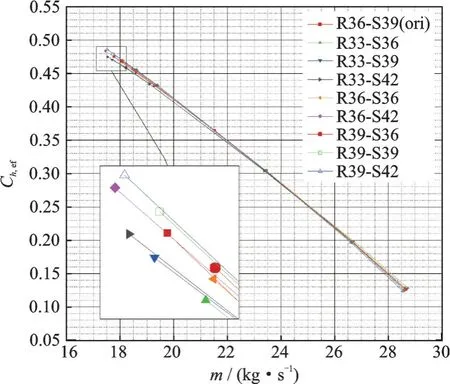
图9 压气机的静压升系数随流量变化曲线Fig.9 Variation curves of compressor static pressure rise coefficient with flow

图10 为叶片数不同时各压气机的最大有效静压升系数对比图，同时，图中还给出了文献［9］提供的最大有效静压升系数关联曲线。从图中可以看出，转静子叶片数不同时，各压气机的最大有效静压升系数较为均匀地分布于Koch 最大有效静压升系数预测曲线的周围，计算所得的最大有效静压升系数的变化趋势与Koch 最大有效静压升系数预测曲线基本一致，但相对位置均有所偏高，表明数值计算得到的不同压气机最大有效静压升略高于预测值。表3 中给出了叶片数不同时，最大有效静压升系数的数值模拟结果、预测值以及两者间的相对误差。由表3 可知，R33-S39 的数值计算结果与预测值的相差最大，但相对误差也仅为3.28%，这说明本文按照Koch 提出的最大有效静压升系数法的数值计算结果与其通过实验结果所得的关联曲线非常接近，表明计算结果的可靠性足够高，同时也从数值模拟的角度验证了以最大有效静压升作为压气机稳定性判据的有效性。为了便于读者对本文计算结果进行验证，表4 给出了R36-S39 算例的详细气动参数。

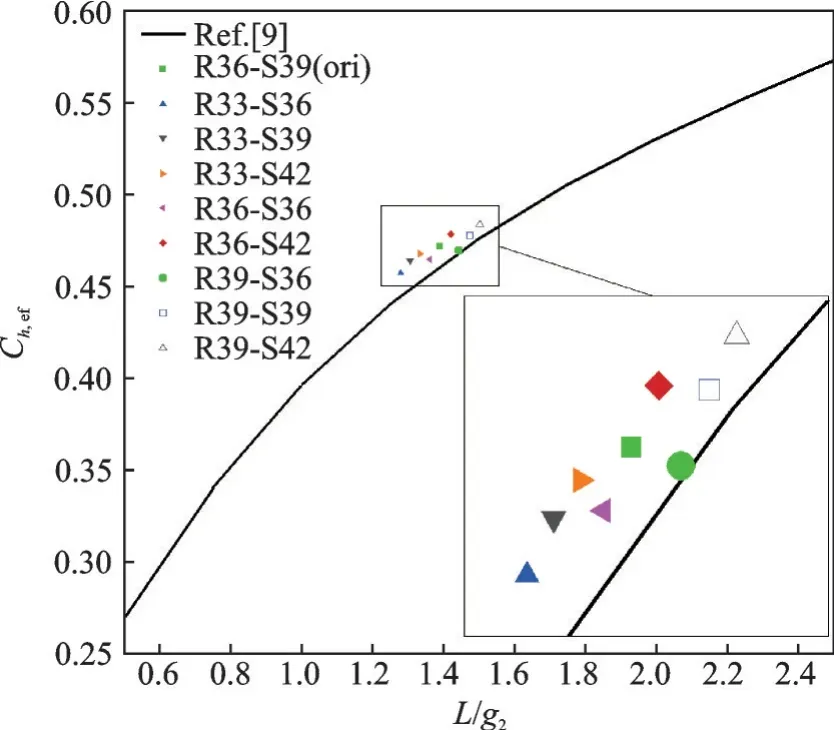
图10 压气机的最大有效静压升系数对比图Fig.10 Comparison diagram of maximum effective static pressure rise coefficient of compressor

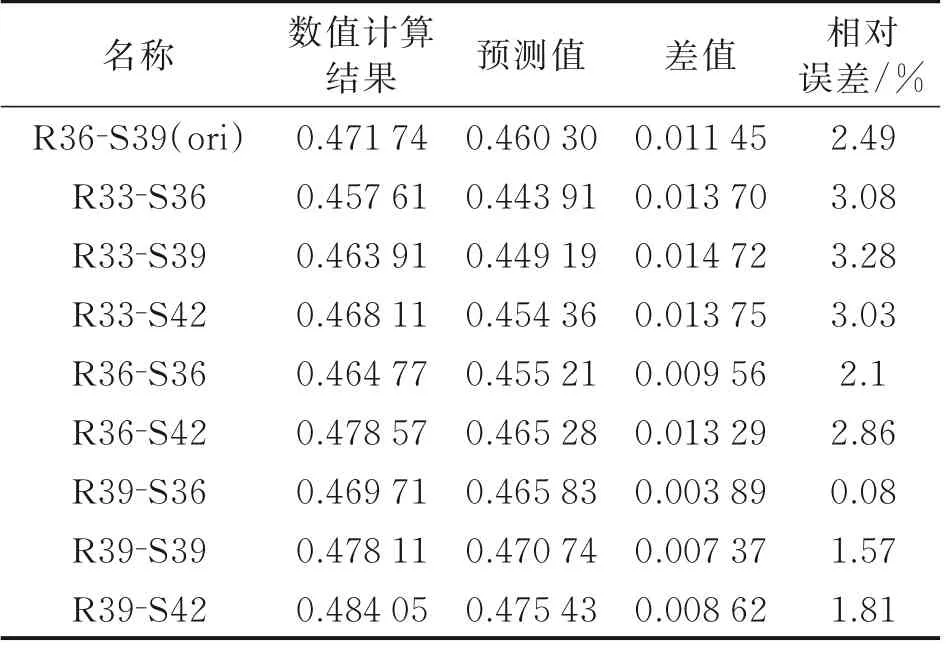
表3 最大有效静压升系数数值计算结果与预测值的对比Table 3 Comparison between numerical calculation results and predicted values of maximum effective static pressure rise coefficient

表4 R36-S39 气动参数Table 4 R36-S39 aerodynamic parameters

其次，通过对各压气机最大有效静压升系数的对比可得，当转子叶片数相同时，压气机的最大有效静压升系数随着静子叶片数的增加而增大，当静子叶片数相同时，压气机的最大有效静压升系数也随着转子叶片数的增加而增大。结合上面的压气机特性曲线可知，当转静子叶片数增加时，压气机近失速点压比均增大，压气机的最大压升能力增强，最大有效静压升系数增大。

5 结论

本文针对某单级低速压气机，通过改变转静子叶片数，构建了不同叶片稠度的压气机模型，通过三维数值模拟的方法，研究了转静子叶片稠度变化对压气机最大有效静压升的影响，得出以下结论：

（1）转静子叶片数的增加都能够抑制附面层分离，减小流动损失，在近失速点，压气机压比随着叶片数的增加而增大，压气机的最大压升能力增强，其最大有效静压升也增大。在叶片数改变时，数值计算所得最大有效静压升系数的变化规律与Koch 最大有效静压升预测曲线的变化趋势相同，即随着叶片稠度的增大，压气机的最大有效静压升系数增大。