离散速度方法及其在跨流域问题中的应用研究进展
杨鲤铭,李志辉,舒 昌,5
(1.南京航空航天大学航空学院,南京 210016;2.南京航空航天大学非定常空气动力学与流动控制工业和信息化部重点实验室,南京 210016;3.中国空气动力研究与发展中心超高速空气动力研究所,绵阳 621000;4.国家计算流体力学实验室,北京 100191;5.新加坡国立大学机械工程系,新加坡 119260)
飞船返回舱、HTV-2、东风-17 等往返大气层与空间轨道跨流域飞行器(图1)的研究,一直以来都备受各军事和航天强国的关注,在载人登月、深空探测和国防领域有着重要的应用价值。然而,由于这类飞行器的飞行高度范围非常大,经常会跨越稀薄流和连续流整个流域范围,对试验研究和数值模拟都提出了严苛的考验[1-5]。一方面,由于这类飞行器所需要考虑的相似参数众多,流动相似准则要求苛刻,地面风洞实验设备对于同时复现其所处的低雷诺数与高焓非平衡流动特征通常无能为力,而且自由飞试验的代价极大,数据采集也非常困难。另一方面,由于飞行轨迹跨越不同的流域,对飞行器的流动模拟需要综合考虑全流域范围的计算精度和计算效率。此外,即便在某一环境克努森数下,飞行器周围流场的局部克努森数也会跨越多个数量级,同时包含连续流、滑移流、过渡区域的高度稀薄流,致使该问题很难被准确高效地求解[1-2,6-8]。

图1 往返大气层与空间轨道跨流域飞行器示意图(图片源于网络)Fig.1 Schematic diagram of flight vehicles covering different flow regimes between the atmosphere and space orbit(pics.from the network)
相较于实验研究,数值模拟无疑是解决该类问题的一种经济有效的手段。但由于稀薄效应的存在,传统的基于连续性假设的Navier-Stokes 方程不再适用于该类问题[9]。为了有效地研究该类问题,通常需要借助于从分子动理学理论(分子运动论)发展而来的Boltzmann 方程。该方程是位置空间、速度空间和时间的七维多相空间几率密度分布函数方程[10],同时其碰撞积分项是一个结构复杂未有明确表达式的五重积分,因而直接求解极为困难。基于该方程,通过合理简化,目前发展了两类典型的数值求解算法。第一类是粒子方法,它通过模拟假想粒子的迁移和碰撞过程来实现对流场的仿真,建模过程等价于对Boltzmann 方程的输运项和碰撞项进行解耦处理。典型代表为直接模拟蒙特卡罗(Direct simulation Monte Carlo,DSMC)方法[4,8,11-13]。第二类是离散速度或离散坐标法(Discrete velocity or discrete ordinate method,DVM 或DOM[14-18]),其在位置空间和速度空间同时离散求解Boltzmann 方程,并且为了避免对碰撞积分不定式的计算,通常采用简化模型来近似碰撞积分项。
DSMC 方法是现阶段解决高超声速飞行器在稀薄流域最有效实用的粒子类方法,由Bird[19]首次提出。该方法的关键是在小于当地分子平均碰撞时间步长Δt内将分子运动和碰撞解耦[3-4,8-9],即让所有分子运动一定距离并考虑边界反射,然后计算此时间段内具有代表性的分子间碰撞。在碰撞取样数趋于无穷大时,DSMC 方法模拟得到的速度分布函数收敛到Boltzmann 方程的修正形式[20]。所以,为了确保模拟不失真,通常要求DSMC 方法的网格尺寸小于分子平均自由程,且时间步长小于分子平均碰撞时间。在稀薄流区域,由于分子数较少,分子平均自由程和平均碰撞时间较大,DSMC方法具有较高的计算效率和计算精度。但在连续和近连续流区域,由于分子平均自由程和平均碰撞时间较小,DSMC 方法的计算效率受到了极大的限制。此外DSMC 方法还存在统计噪声问题,以及不便应用于非定常流动模拟和不易于采用隐式算法加速等困难。为了应用于跨流域问题的求解,一些学 者 提 出 了Navier-Stokes/DSMC 耦 合 算 法[21-23],其思想是将计算域划分为不同的子区域分别应用DSMC 方法和Navier-Stokes 方程求解器进行求解。虽然该类耦合算法能在各自的区域获得准确高效的计算结果,但区域划分和不同区域间的数据交互较为困难,而且一般还需要设置缓冲区。Torre等[24]发现,该类耦合算法的计算结果对区域划分和缓冲区的设置非常敏感。近年来,一些改进的粒子类方法也被相继提出用于克服原始DSMC 方法在低速流动统计噪声过大的问题,以及在连续和近连续流区域网格尺寸和时间步长受限于分子平均自由程和分子平均碰撞时间的不足。例如,Sun 和Boyd[25]提出了DSMC 信息保存(Direct simulation Monte Carlo-information preservation,DSMC-IP)方法;Fei 等[26]提出了多尺度的统一粒子BGK(Unified stochastic particle-BGK,USP-BGK)方法等。
不同于粒子类方法,DVM 直接更新离散分布函数,有效避开了统计噪声问题,并且可以方便地引入传统计算流体力学的隐式加速算法来提高计算效率。在DVM 框架下,通过引入气体分子碰撞松弛参数和当地平衡态速度分布函数来建立Boltzmann 方程碰撞积分统一模型,同时利用高效算子分裂方法和大规模并行技术来求解该模型方程,Li 和Zhang[27]提 出 了 气 体 动 理 论 统 一 算 法(Gas kinetic unified algorithm,GKUA);通过利用Boltzmann-BGK 方程的局部积分解来同时计算介观 方 程 和 宏 观 伴 随 方 程 的 通 量,Xu 和Huang[28]提出了统一气体动理学格式(Unified gas kinetic scheme,UGKS);通过利用Boltzmann-BGK 方程的局部特征解来计算介观方程的通量,Guo 等[29]提出了离散统一气体动理学格式(Discrete unified gas kinetic scheme,DUGKS)。随后,Chen 等[30]通过对介观方程和宏观伴随方程的通量进行简化,提出了简化版本的UGKS;通过引入LU-SGS 技术和多重网格加速收敛技术,Zhu 等[31]改进了UGKS 的计算效率。此外,在采用传统DVM 求解介观方程的基础上,通过引入宏观伴随方程并利用含碰撞项Boltzmann-BGK 方程的局部解来计算该方程通量,Yang 等[32]提 出 了 改 进 离 散 速 度 方 法(Improved discrete velocity method,IDVM);Su 等[33]通过在计算宏观伴随方程通量时引入高阶修正项,提出了合成迭代加速算法(General synthetic iterative scheme,GSIS)。由于在通量计算过程中同时考虑了分子迁移和碰撞的影响,基于DVM 框架发展的算法的网格尺度和时间步长不再受限于分子平均自由程和平均碰撞时间,因而有效地克服了DSMC 方法在连续和近连续流区域的计算困难,实现了全流域的统一求解。
但由于需要在位置空间和速度空间同时离散,DVM 所需的存储量和计算量非常大,因而早期发展较为缓慢。近年来,随着计算机内存和运算速度的提升,基于DVM 框架发展的算法已取得了喜人的成绩并逐渐被应用于航天科技、微电子机械系统和真空技术等多个领域。本文首先对该类方法的研究进展进行回顾,尤其是GKUA 和UGKS 两种算法的构造途径,并介绍他们在跨流域问题中的应用。随后,本文将介绍作者团队近年来发展的IDVM 及其研究进展,并通过引入双时间步格式构造非定常隐式IDVM,用于非定常跨流域问题求解。最后,通过剖析基于DVM 框架发展的数值方法面临的挑战,展望未来跨流域问题的一些研究方向。
1 Boltzmann模型方程和DVM框架
1.1 Boltzmann 模型方程和速度空间离散
通过引入气体分子速度分布函数f,则气体动力学中感兴趣的各种宏观量便可以通过对f求矩而得到。由此可见,除了采用常见的宏观守恒律方程,流体系统亦可由分布函数f的演化方程来描述。1872 年,Boltzmann 给出了分布函数对位置空间、速度空间和时间的变化率的关系,即Boltzmann 方程
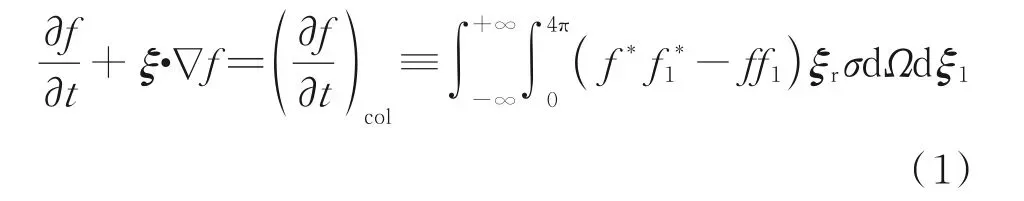

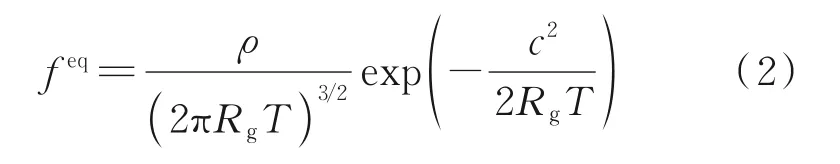
式中:c=ξ-u为分子的最可几热运动速度;u为宏观速度;ρ为密度;T为温度;Rg为气体常数。除特殊说明外,本文中约定用黑体来表示矢量,用对应的白斜体来表示矢量的长度。
依据速度分布函数f的定义以及分子碰撞过程中的质量、动量和能量守恒关系(即相容性条件),气体动力学中常见的宏观量可以表示为


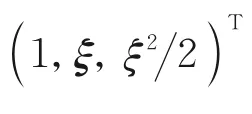
由于方程(1)的碰撞项过于复杂且对于流体力学计算难以形成明确的数学表达式,在速度空间直接离散求解该方程对于实际问题的表征难有意义[34]。因此,各类简化的碰撞模型被提出用于近似该碰撞项,例如BGK 模型[35],ES-BGK 模型[36]和Shakhov-BGK 模型[37]等。BGK 模型由Bhatnagar,Gross 和Krook 提出,它可以满足质量、动量和能量守恒,满足熵增条件,并且导出的平衡态即为Maxwell 分布。但是,该模型对应的普朗特数为1,与通过原始方程(1)推导得到的正确值2/3 不一致,因此不能同时保证正确的黏性系数与热导率。ES-BGK模型由Holway 提出,通过在平衡态分布函数中引入应力修正项来实现对BGK 模型普朗特数的修正;Shakhov-BGK 模型则通过在平衡态分布函数中引入热流修正项来实现对BGK 模型普朗特数的修正。由于可以恢复正确的普朗特数,ES-BGK 模型和Shakhov-BGK 模型都能同时保证正确的黏性系数与热导率。但大多数情况下Shakhov-BGK 模型的精度优于ES-BGK 模型,因此Shakhov-BGK 模型获得了更广泛的应用[38]。采用Shakhov-BGK 模型作为碰撞项的Boltzmann 方程可以改写为

式中Pr为普朗特数。相较于方程(1),采用方程(7)可使得求解过程大为简化。因此,目前基于DVM 框架发展的算法大都是直接求解方程(7)。
虽然Boltzmann 模型方程的碰撞项已大为简化,但分布函数f仍然是时间、位置空间和速度空间的七维变量,需要离散化方能数值求解。DVM首先在速度空间对Boltzmann 模型方程进行离散,获得离散速度形式的Boltzmann 模型方程


由于速度空间的网格量直接影响DVM 的计算量和存储量,为了尽可能优化速度空间的网格分布,Gutnic 等[43]、Kolobov 和Arslanbekov[44]、Chen等[45]发展了速度空间自适应DVM。该方法的内存需求相较于采用均匀网格的Newton-Cotes 求积可以降低1~2 个数量级,但由于采用自适应算法之后不同位置空间网格的分布函数对应的离散速度不一致,需要频繁的插值运算,程序处理较为复杂。最近,Zhao 等[46]采用降阶模型对计算结果进行模态分析,通过提取主导模态对应的离散速度点,并仅更新这些离散点的分布函数,有效减少了DVM 的计算量。但由于不同来流参数对应的主导模态不一致,该方法仅适用于来流参数变化较小的流动问题求解。为了应对工程实际问题中通常需要计算一系列不同来流参数工况的情形,Yang等[47]进一步提出了基于参数化的降阶离散速度方法。首先,从全部工况中挑选少数工况作为预计算工况,并利用IDVM 计算其结果。其次,基于这些预计算工况得到的离散分布函数,采用奇异值分解求出主导模态对应的降阶子空间,并利用对数和指数映射,在Grassmann 流型及其切空间上插值计算其余工况所对应的降阶子空间。最后,通过离散经验插值算法搜寻降阶子空间对应的离散速度点,从而构成缩减的离散速度空间。基于此,其余工况便可以直接在对应的缩减离散速度空间上进行求解,从而有效地减少了计算量。
此外,由于DVM 中采用数值求积来计算宏观量,其结果必然会与直接积分存在误差,因而导致相容性条件不能精确满足,影响结果精度和数值稳定 性。为 了 解 决 这 一 问 题,Titarev[48],江 定 武等[49],Yang 等[50]发展了守恒型DVM,通过引入内迭代强制满足相容性条件。采用该类方法可以在较稀的速度空间网格上得到网格无关解,减少的计算量最大可达2/3。
1.2 GKUA 研究进展
针对航天飞行器再入各流域多尺度非平衡绕流特点,为了反映再入过程不同流域气体分子相互作用、稀薄程度、分子模型与内部能量变化关系,通过引入气体分子碰撞松弛参数ν和当地平衡态速度分布函数fS来模型化表征Boltzmann 方程碰撞积分项对航天飞行器再入跨流域气动力/热绕流特性,可确立描述各流域全局马赫数复杂流动输运现象统一的Boltzmann 模型速度分布函数方程,其无量纲形式为

由此,可将最新的计算流体力学中的有限差分格式等引入到基于离散速度坐标形式的Boltzmann 方程中,在位置空间和时间方向对该方程进行求解。基于此,Li 等[51-52]提出了GKUA用于模拟高超声速跨流域流动问题。其中,采用算子分裂思想结合二阶显式Runge-Kutta 方法和无波动、无自由参数、具有耗散性(Nonoscillatory nonfree dissipative,NND)差分格式[53],方程(10)可以在位置空间和时间方向进一步离散为
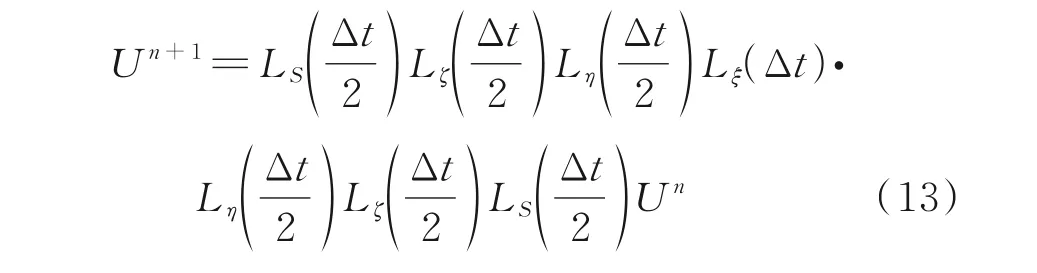
式 中:LS、Lξ、Lη、Lζ分 别 为 如 下 方 程 的 二 阶 差 分算子

完成分布函数更新后,便可利用方程(3)和方程(6)计算新时刻的守恒量和热通量,并利用方程(2)和(8)计算新时刻的当地平衡态分布,从而开始下一时刻推进求解。该方法中,时间步长Δt仅由差分格式稳定性条件决定,与当地气体分子平均碰撞时间无关[3,20,34,52]。另外,由于其宏观流动量是通过离散速度分布函数对所有离散速度坐标点进行离散积分归约求和来更新,与常规计算流体力学位置空间具体网格尺度无关,因而位置空间流场网格划分不受任何限制,可在大尺度网格快速计算收敛,确保了GKUA 计算复杂飞行器高超声速气动力/热绕流特性,解决实际应用问题的准确可行性[54-59]。
除了有限差分格式,吴俊林等[55]还发展了基于有限体积格式的GKUA。另外,为了提高计算效 率 和 稳 定 性,Peng 等[56]发 展 了 隐 式 版 本 的GKUA。由于仅求解介观Boltzmann 型速度分布函数方程并且在同一时间步内每个离散速度坐标点处的分布函数的求解是相互独立的,GKUA 的计算过程较为简单,且非常易于在离散速度空间分块并行求解。基于HPF、MPI+OpenMP、MPI+OpenACC 程序构架,各种并行版本的GKUA 被提出并应用于跨流域工程实际问题求解。此外,考虑到高温多原子气体必然会存在转动和振动自由度,为了准确模拟高温高马赫数下多原子气体内能激发对跨流域非平衡流动的影响,李志辉等[57]发展了同时考虑平动-转动能松弛特性的GKUA,彭傲平等[58]发展了同时考虑平动-转动-振动能松弛特性的GKUA。 应用发展的算法,李志辉等[3,6,27,34,52,57]构建了适用于返回舱从外层空间自由分子流再入到近地面连续流的跨流域空气动力学一体化模拟平台。图2 展示了采用该平台计算得到的返回舱再入120~70 km 流场压力分布。最近,结合空间站建设与运维,为了研究服役期满大型航天器如空间实验室、货运飞船等再入气动力/热环境致结构变形/失效解体的非线性力学响应行为,李志辉等[54,59]将瞬态热传导方程与材料热弹性动力学方程引入GKUA 中,构建了跨流域动态力/热耦合计算平台,实现了再入强气动力/热环境致材料变形/失效解体的统一求解,如图3 所示。研究表明,GKUA 作为一种基于气体分子速度分布函数演化更新实时捕捉宏观气体流动特征的介观模拟方法,可以较好地求解全流域气体流动问题,在航空航天领域得到了成功运用。目前算法考虑了多种非平衡效应,包括平动-转动非平衡、平动-转动-振动非平衡,建立了可靠模拟大型复杂结构航天器(如我国天宫一号目标飞行器)服役期满离轨陨落再入解体跨流域高超声速气动力/热非平衡绕流问题的气体动理论统一算法大规模并行计算应用研究平台。

图2 返回舱以第一宇宙速度7.5 km/s 再入跨流域(120~70 km)气动模拟软件系统实时计算与姿态配平绕流压力分布[3]Fig.2 Real-time computing pressure distribution during the spacecraft capsule re-entry (120—70 km) with the first cosmic velocity of 7.5 km/s[3]
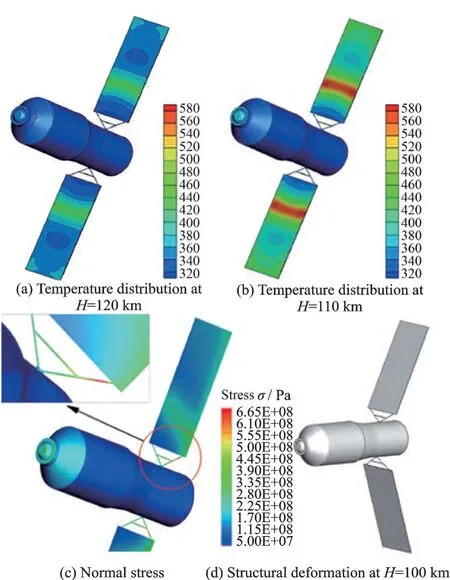
图3 类天宫飞行器在H = 120~100 km、v∞= 7.6 km/s 条件下强气动力/热环境致结构温度变化和稳态变形[54]Fig.3 Temperature distributions and steady-state deformation of structure at H = 120—100 km and v∞=7.6 km/s around Tiangong type spacecraft by strong aerodynamic heating[54]
1.3 UGKS 研究进展
与GKUA 不同,UGKS 同步求解了介观的Boltzmann 模型方程和对应的宏观伴随方程。宏观伴随方程实际上对应于Boltzmann 模型方程在速度空间求守恒矩

式中:xij为单元界面位置;f(xij,ξα,t)为单元界面上的离散分布函数;f(xij-ξαt,ξα,0)为单元界面周围的初始离散分布函数;fS(xij-ξα(tt′),ξα,t′)为t′时 刻 单 元 界 面 周 围 的 平 衡 态 分 布 函数。实际计算中,f(xij-ξαt,ξα,0)可由n时刻单元中心的离散分布函数插值计算得到,而平衡态分布fS(xij-ξα(t-t′),ξα,t′)则 可 由 宏 观 物 理 量 及其导数来计算。最终,f(xij,ξα,t)可写为

由于f(xij,ξα,t)是时间的函数,通量计算时需要取其在(0,Δt)积分的时间平均
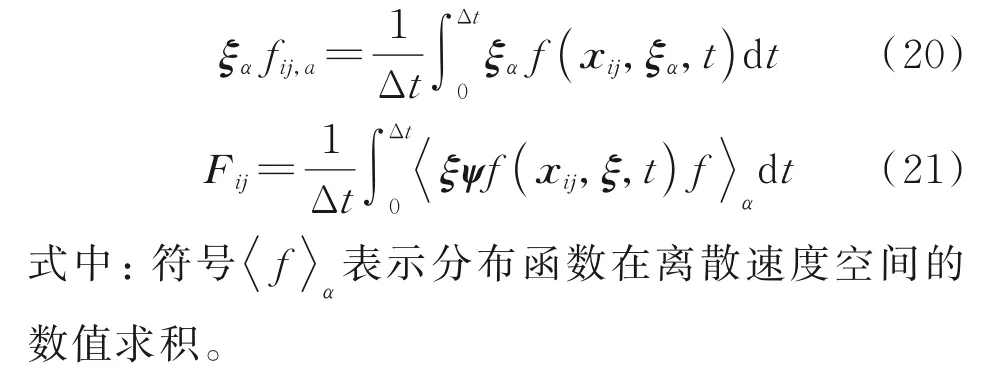
由方程(18)可知,当分子迁移时间远小于分子平均碰撞时间时(t≪τ),单元界面分布函数中初始分布f(xij-ξαt,ξα,0)占主导,表现为自由分子流情形的完全自由迁移现象;而当分子迁移时间远大于分子平均碰撞时间时(t≫τ),单元界面周围的平衡态分布fS(xij-ξα(t-t′),ξα,t′)占主导,表现为连续流情形的分子频繁碰撞现象。由于实际计算中分子的迁移时间即为网格尺度对应的时间步长Δt,方程(18)等效于在网格尺度上的流动建模,将主导稀薄流的分子自由迁移机制和主导连续流的分子碰撞机制的权重与网格尺度有机联系起来。由于通量计算时分子的迁移和碰撞过程相互耦合,UGKS 的推进时间步长不受限于当地分子的平均碰撞时间,且其网格尺度也不受限于当地分子平均自由程,从而使得该方法在全流域均可获得准确高效的计算结果。
基于上述优势,UGKS 已成功应用于从连续到稀薄流的许多流动计算中。例如,Liu 等[61]发展了同时考虑平动-转动能松弛特性的UGKS;Wang等[62]发展了同时考虑平动-转动-振动能松弛特性的UGKS;Sun 等[63]将UGKS 应 用 于 辐 射 传 热 问题;Xiao 等[64]将UGKS 应用于多组分流问题;Liu和Xu[65]将UGKS 应用于等离子体问题;Tan 等[66]将UGKS 应 用于中子输 运问题;Liu[67]将UGKS 应用于颗粒流问题等。同时,为了进一步提高UGKS的 性 能,Chen 等[68]和Yang 等[69]发 展 了 内 存 缩 减UGKS 用于定常跨流域流动问题的求解;Zhu等[70-71]发展了隐式版本的UGKS 用于定常和非定常流动问题求解,使得计算效率提高了1~2 个数量 级。应用UGKS,Li 等[72]模拟了类X38 高超声速飞行器在不同克努森数时的气动力/热问题并与DSMC 结 果 进 校 了 比 较,如 图4 所 示。Chen 等[45]结合动网格技术,应用UGKS 模拟了稀薄环境下喷流推进问题,如图5 所示。该问题中,喷管内部为连续流动,而喷管外部为稀薄流动,因此需要保证算法在连续到稀薄整个流域范围都能获得可靠的计算结果。

图4 采用UGKS 和DSMC 计算的类X38 飞行器温度场比较(Argon, α=20°)[72]Fig.4 Comparison of temperature contours of X38-like model[72]

图5 稀薄环境下喷管喷流计算结果[45]Fig.5 Numerical results of gas injection to the rarefied atmosphere[45]
1.4 IDVM 研究进展
GKUA 仅求解Boltzmann 型速度分布函数方程,而且同一时间步内每个离散分布函数的演化是相互独立的。因此,该算法实施较为简单,且非常易于在离散速度空间分块并行求解。由于其与分子层级的迁移和碰撞解耦无关,GKUA 的时间步长仅由所使用的差分格式的稳定性条件决定。不仅时间步长与分子平均碰撞时间无关,而且位置空间网格划分尺度也与气体分子平均自由程无关,确保了GKUA 在大网格尺度计算复杂高超声速飞行器气动力/热非平衡绕流问题的高可靠性与工程置信度。然而,由于GKUA 的宏观量由当地各离散速度坐标点的分布函数实时归约求和进行更新,Boltzmann 型速度分布函数方程的碰撞项和对流项同步显式或隐式离散差分计算,对连续流问题的求解按所用差分格式稳定性条件确定的时间步长会使得收敛变慢。相比较而言,UGKS 同步求解了Boltzmann 模型方程和相应的宏观伴随方程,并将分子的迁移和碰撞过程耦合处理。同时,由于同步求解了宏观伴随方程,其结果可用于预估新时刻的平衡态,从而实现了Boltzmann 模型方程中碰撞项的全隐式离散,保证了连续流区域的计算效率。但是,由于通量计算时所采用的Boltzmann-BGK 方程的局部积分解较为复杂,稀薄流区域的计算效率受到了一定的影响,而且为了获得单元界面的积分解,需要联立界面周围所有的离散分布函数来计算界面的平衡态分布。
在上述两种算法的启发下,为了保证从稀薄到连续整个流域范围的计算精度和计算效率,同时使算法的实施较为简单,Yang 等[73]发展了IDVM。与UGKS 类似,该算法也同步求解了Boltzmann 模型方程和相应的宏观伴随方程,以便实现Boltzmann 模型方程中碰撞项的全隐式离散。但不同于UGKS,IDVM 在求解Boltzmann 模型方程时仍然将分子的迁移和碰撞过程解耦处理,以便保持同一时间步内每个离散分布函数的演化相互独立的优势。此外,为了提高连续流区域的计算精度和计算效率,IDVM 在求解宏观伴随方程时同时考虑了分子的迁移和碰撞过程对通量计算的影响。具体地,IDVM 将Boltzmann 模型方程和相应的宏观伴随方程离散为如下形式

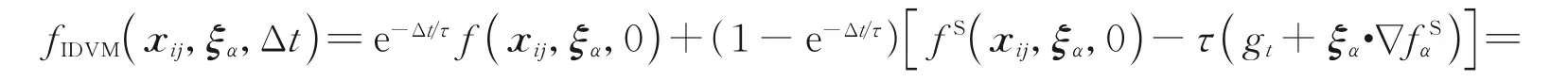

式中:fDVM为不含碰撞项Boltzmann 方程在单元界面的局部解,即方程(25);fNS为对应于连续流极限的分布函数。将方程(26)代入方程(4),即可得到宏观伴随方程的通量

由方程(25)和方程(26)可知,IDVM 在计算Boltzmann 模型方程通量和宏观伴随方程通量时所采用的单元界面分布函数是不一样的。原因在于,采用不考虑分子碰撞影响的分布函数来计算Boltzmann 模型方程的通量虽然会影响该方程在连续流区域的计算精度和计算效率,但却可以保证同一时间步内每个离散分布函数的演化是相互独立的,以保持算法的简单性。实际上,在连续流区域由宏观伴随方程主导流场的解,而且此时宏观伴随方程的通量即为Navier-Stokes 方程的通量,因此只要引入合理的宏观伴随方程即可获得该区域的准确计算结果。综上所述,该策略既保持了原始DVM 的简单性优势,也提高了连续流区域的计算精度和计算效率。但是,由于Boltzmann 模型方程的通量和宏观伴随方程的通量计算不一致,该方法在理论上还存在不自洽的问题,其具体影响和改进措施还有待进一步研究。最近,通过引入LU-SGS迭代,Yang 等[74]发展了三维隐式IDVM 用于定常跨流域流动问题的求解。如图6 所示,在连续流区域,IDVM 相较于传统DVM 计算精度更高,且计算效率提高了1~2 个数量级。另外,通过引入内迭代技术,Yang 等[75]实现了定常IDVM 计算效率的进一步提升,并模拟了高超声速稀薄流状态下的猎户座飞船返回舱的气动力/热问题,如图7 所示。

图6 三维顶盖驱动流问题的计算结果[74]Fig.6 Numerical results for 3D lid-driven cavity flow[74]
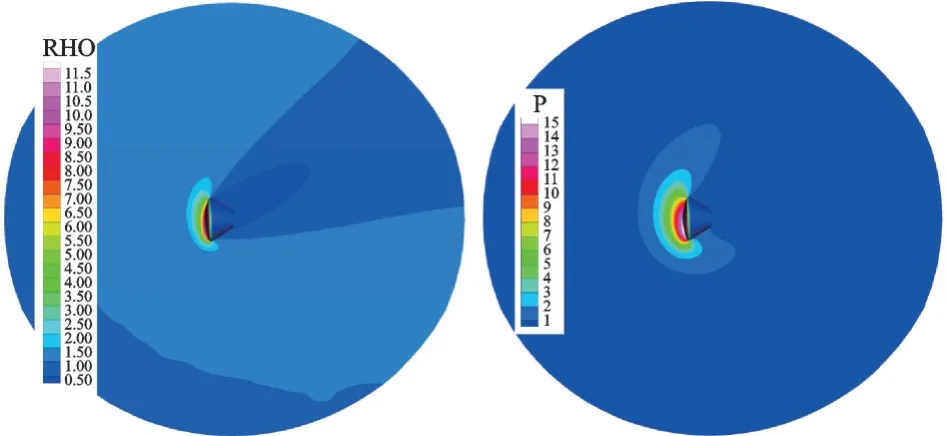
图7 猎户座飞船返回舱高超声速稀薄流的密度和压力分布[75]Fig.7 Density and pressure contours for hypersonic rarefied flow around an Orion crew module[75]
2 非定常隐式IDVM 及其应用
2.1 非定常隐式IDVM
为了实现非定常跨流域流动问题的准确高效求解,本文将先前发展的隐式定常IDVM 进一步拓展到了非定常情形。基于双时间步LU-SGS 迭代的思想,在Boltzmann 模型方程和宏观伴随方程中同时增加了伪时间导数项


2.2 算例验证
为了验证上述非定常隐式IDVM 的性能,本文模拟了墙壁束缚瑞利流,并将计算结果与非定常隐式UGKS 进行比较。如图8 所示,初始时刻两个间隔1 m 长4 m 的平行平板之间充满静止的氩气。平板的温度和氩气的温度均为273 K,氩气的分子质量为6.63×10-26kg,对应的气体常数为Rg=208.13 J/(kg·K)。启动瞬间,左右两侧的平板以10 m/s 的速度向上运动,平板温度为373 K。由于几何对称性,实际计算中仅考虑左半侧区域流场。
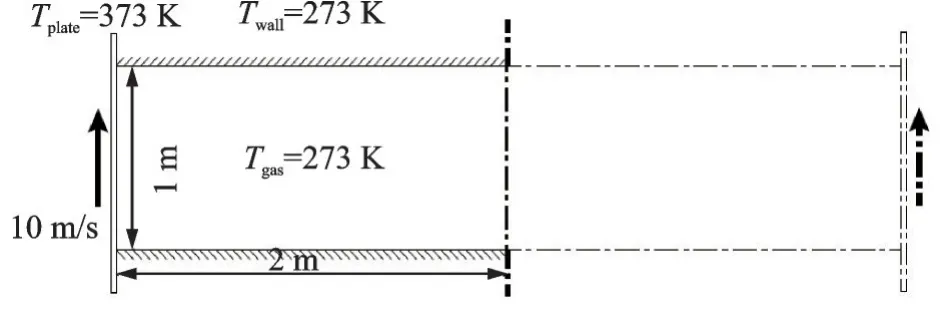
图8 墙壁束缚瑞利流示意图[71]Fig.8 Schematic for wall-bounded Rayleigh flow[71]
为了与文献条件一致,本文将该算例的克努森数取为Kn= 0.05。分子速度空间采用包含28×28 个离散点的Gauss-Hermite 积分,位置空间采用12 800 个均匀四边形非结构网格进行离散。无量纲的外迭代时间步长取为Δt=0.01。图9 展示了t= 1.5 时刻水平和垂直中心线温度、x方向速度分量和y方向速度分量分布,当前计算结果与UGKS结果较好吻合。另外,图10 展示了t= 1.5 时刻上下平板的压力、热通量和切应力分布,当前结果也与GUKS 结果吻合良好。该算例验证了提出的方法在非定常跨流域流动的计算能力。

图9 墙壁束缚瑞利流在Kn = 0.05 和t= 1.5 时水平中心线和垂直中心线流动变量分布图Fig.9 Flow variables along the horizontal and vertical central lines for wall-bounded Rayleigh flow at Kn = 0.05 and t= 1.5

图10 墙壁束缚瑞利流在Kn = 0.05 和t= 1.5 时上下表面流动变量分布图Fig.10 Flow variables along the upper and bottom surfaces for wall-bounded Rayleigh flow at Kn = 0.05 and t= 1.5
3 总结与展望
本文首先回顾了基于速度空间离散的几类Boltzmann 模型方程求解算法,展示了它们在低速到高超声速、连续到稀薄全流域范围的应用。同时,本文还将笔者前期发展的定常隐式IDVM 扩展到了非定常情形,并通过非定常跨流域问题进行了验证。这类方法由于直接演化分布函数,可以有效避免粒子类方法的统计噪声问题,同时可以采用传统计算流体力学中的加速技术来提高计算效率。在微电子机械和真空技术等低速跨流域问题以及不含离解和电离化学非平衡效应的高速跨流域问题中,该类算法已经展现出一定的优势。但是对于航天领域涉及的高温高速和真实气体效应的非平衡流动,该类算法也还存在许多丞待解决的问题,需要持续不断地改进完善。
(1)由于基于DVM 框架发展的算法需要在位置空间和速度空间同时进行离散,因而实际工程问题的计算量和内存开销非常大。尤其是对于高超声速跨流域问题,由于流动速度和温度非常高,速度空间截断区域也需要相应扩大,方能保证求矩计算宏观量的精度。最近,Liu 等[76]和Xu[77]提出了统一气体动理学波粒子(Unified gas kinetic wave particle,UGKWP)方法,采用粒子来表征稀薄效应部分的贡献,而连续效应部分的贡献直接采用解析的方式来计算。在连续流区域,UGKWP 方法自动退化为Navier-Stokes 方程求解器,而在稀薄流区域,该方法也具有粒子在速度空间自适应分布的优势。但是,由于引入了粒子的计算,UGKWP 方法同样也存在统计噪声问题,以及不便应用于非定常流动求解和不易于采用传统计算流体力学的加速技术来提高计算效率的问题。
(2)在Boltzmann 模型方程中,每增加一种能量松弛方式和化学组分,都需要增加相应的分布函数来对其进行描述。对于高超声速稀薄流动问题,由于温度通常高达10 000 K,不仅需要考虑分子的转动松弛和振动松弛,还需要考虑离解和电离化学非平衡效应,这给基于DVM 框架发展的算法带来了极大的困难和挑战。一方面是如何建立合理的模型方程,另一方面是如何设计针对模型方程的高效数值算法。文献[78]从量子力学的角度出发建立了WCU 方程,对每个能级的分布函数写出了一个Boltzmann 方程,其迁移项保持不变,而碰撞项是单组分Boltzmann 方程碰撞项的唯象扩展。该模型方程有望实现对真实气体效应的模拟,但由于求解困难,目前文献中尚未发现可工程实用的相应算法。

