机动弹头舵轴热环境分析

张志刚，赵金山，粟斯尧，孔荣宗，陈 挺

（1.南京航空航天大学航空学院，南京 210016；2.中国空气动力研究与发展中心超高速空气动力研究所，绵阳 621000）

为了实现高机动性，高超声速机动弹头一般在尾部布置有若干气动舵［1-2］，例如美国的“潘兴Ⅱ”导弹（图1），气动舵和弹体通过舵轴连接，两者之间会存在几毫米高的缝隙，如图2 所示［3］。有迎角情况下缝隙内的流动非常复杂，舵轴前缘等位置可能存在热流峰值，对弹体产生破坏，因此需要对偏转缝隙内部的热环境进行准确预测［4-8］。但目前国内外对舵轴缝隙的局部热环境开展的研究相对较少［9-18］，对舵轴及其干扰区热流的量值和变化规律尚未有明确的认识。其原因主要有两个方面，一是目前高超声速机动弹头的控制舵通过舵轴与弹身连接，从飞行器前体发展而来的气流进入舵轴缝隙后受到强压缩作用，进而产生复杂的流场结构造成理论计算的难度很大，且计算代价极大，在机理研究方面无法提供完备的数据支撑。二是由于风洞尺寸的限制，往往需要对模型进行缩比，而由于缝隙的尺寸相对于弹体只有千分之一量级，缝隙尺寸也远远小于当地边界层厚度，如果对弹体直接进行缩比试验，有可能得到的试验结果与真实情况相差很大，不能真实模拟飞行条件下缝隙内部的流动状况；如果采用局部试验模型，如何模拟当地的流动情况成为试验的难题。

图1 美国“潘兴Ⅱ”导弹Fig.1 Pershing 2 ballistic missile

图2 高超声速飞行器空气舵安装示意图[3]Fig.2 Installation diagram of air rudder for hypersonic vehicle[3]

因此，关于高超声速机动弹头舵轴热环境的研究相对较少。目前随着高超声速飞行器的发展，舵轴区域的热防护设计对局部热环境的预测精度提出了更高的要求，如何解决这一难题迫在眉睫［19］。

目前的有效手段是理论计算与风洞试验相结合，即通过可靠的理论预测手段，分析舵轴及其干扰区峰值热流随迎角、舵偏角、缝隙高度等因素的变化规律，从而构造合理的试验模型，并开展风洞试验，利用风洞试验结果和理论研究得到的规律，去预测飞行条件下的热环境［20-21］。

本文基于这一思想，利用风洞试验与理论研究相结合的方法对舵轴的局部热环境进行研究。首先构建长约1 m 的球双锥带舵外形，然后在激波风洞上开展测热试验，获得大面积区域、舵轴等位置的热流分布，同时针对试验工况开展Navier-Stokes方程（N-S 方程）数值模拟，与激波风洞试验结果进行对比，验证方法的可靠性。在此基础上，对相同高度，不同马赫数、不同迎角、不同舵偏情况下开展大量的数值模拟，获得舵轴热环境随马赫数、迎角、舵偏角等因素的变化规律，最终建立多参数插值拟合方法，通过该方法可以对舵轴峰值热环境在不同飞行状态下的热流变化开展快速预测。

1 试验设备及流场条件

1.1 试验设备及测量手段

舵轴缝隙热环境试验在Φ2 m 激波风洞（FD-14A，如图3 所示）上开展。该风洞是由内径150 mm 的激波管和相应的喷管、试验段、真空箱组成，其型面喷管出口直径为1.2 m，锥形喷管出口直径为2 m，试验段横截面积为2.6 m×2.6 m。风洞试验气体为氮气，采用氢气或氢气与氮气混合气体驱动，驱动压力可达60 MPa，模拟最高总温为4 000 K。风洞通过更换喷管及喉道来获得不同的来流马赫数，通过调节高低压段的压力来获得不同的雷诺数，以实现不同的模拟环境。该风洞可模拟的马赫数范围是6～24，单位雷诺数范围是1×10-6～1×10-8m-1，试验有效时间为4～18 ms。

图3 Φ2 m 激波风洞（FD-14A）Fig.3 Φ2 m shock wind tunnel（FD-14A）

试验中主要采用的测量手段有Φ/2 mm 点式铂薄膜热流传感器和型面热流传感器，如图4 所示。其中，点式铂薄膜热流传感器主要用于测量舵基板、舵底及弹身大面积区热环境，型面热流传感器用于测量舵轴曲面的热环境。

图4 两种热流传感器Fig.4 Two kinds of heatflux sensors

1.2 试验模型及流场条件

试验模型采用圆锥带舵外形，模型总长约1 m，4 个三角舵呈十字布局安装在模型尾部，如图5 所示。为了便于表述，按照正迎角时的来流方向，将模型上的舵面根据位置不同分别称为迎风舵、水平舵和背风舵。空气舵与模型身部通过舵轴连接，舵缝隙高度约2.5 mm，舵轴中部沿周向均布8 个热流传感器（图5（c））。试验来流马赫数约为10，Re/L≈2×107m-1，测量迎角为20°，边界层在舵前完全转捩为湍流。

图5 飞行器舵面位置示意图Fig.5 Diagram of the vehicle rudder

1.3 数值计算方法

本文采用有限体积方法离散求解三维直角坐标系下的完全气体N-S 方程［22］。

通过对网格控制体单元内的无黏通量与黏性通量进行积分，同时结合Gauss 定理［23］。本文将耗散大的矢通量分裂格式Steger-Warming 格式［24］与耗散小的基于解析黎曼求解器的Godunov 格式［25-26］混合使用，以提高计算稳定性，同时使格式在边界层模拟中具有低耗散特性［27］。无黏项采用隐式格式，黏性项采用显示二阶中心格式，最后采用LU-SGS 方法［28-29］进行时间推进求解，并使用局部时间步长加速计算收敛。由于本文计算的工况主要为低空高雷诺数湍流工况，采用的湍流模型为目前较为常用的k-ωSST 湍流模型［30-33］。

本文采用的计算网格及边界条件如图6 所示。其中深红色网格对应固壁边界，设置为无滑移等温壁条件，壁面温度Tw=283 K；粉色网格对应自由来流边界，具体参数如表1 所示；绿色网格对应超声速外推出口边界。特别值得指出的是，由于在风洞试验中，模型位于流场核心区内，且气流方向与模型中心线完全一致，因此为节省计算量，本文仅采用半模开展了数值模拟，蓝色网格设置为对称边界。网格数为271（流向）×241（周向）×81（法向）个，且为保证边界层内流动结构的模拟，在靠近壁面附近进行了网格加密，壁面法向第一层网格间距为2×10-3mm。

图6 网格示意图Fig.6 Computation grid

需要指出的是，为验证计算结果的网格无关性，本文对3 个方向的网格进行了加密。结果表明，加密网格后计算得到的流场结构和物面热流分布均与加密网格前的计算结果基本一致。

以上分析表明，本文采用的数值模拟方法可以正确模拟激波干扰类型，具有较高精度和较好的网格无关性，可用于开展舵轴热环境计算分析。且为减少计算量，本文后续在开展所有工况的计算仿真时，均采用原始3 个方向没有进行加密的网格，仅在有舵偏角情况下，对舵偏进行了调整，整体网格拓扑结构、网格量及法向第一层网格间距保证不变。

1.4 试验结果对比验证

为验证计算方法的可靠性，首先针对模型在Ma≈10、Re/L≈2×107m、迎角约20°条件下，开展了数值仿真，并与风洞测热试验数据开展了对比分析。图7 是20°迎角时弹体下表面中心线热流计算与试验结果比较，纵坐标为热流，横坐标为从驻点开始沿0°子午线至舵根前沿垂直投影到模型身部的x向长度。图中的点为试验结果，曲线为数值计算结果，可以看出，在第一锥的锥面上x=0.05 m附近发生了转捩，热流明显上升，在第二锥上由于半锥角较第一锥要小，热流下降至一个平台。从结果对比来看，试验数据存在一定的波动，但总体而言计算结果和试验结果吻合较好。证明在大面积区域本文采用的数值计算方法较为可信。

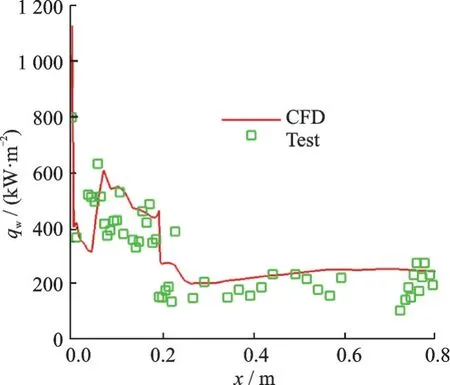
图7 20°迎角时弹体下表面中心线热流对比分析Fig.7 Comparative analysis of heatflux in the center line of the lower surface of the missile at 20 degree of attack

图8 是Ma≈10、Re/L≈2×107m-1、迎 角20°条件下水平舵轴表面热环境计算与试验结果的对比，纵坐标为热流，横坐标为沿舵轴中部一周的角度，其中舵轴朝向弹体头部方向为Φ=0°，逆时针沿舵轴轴向半周朝向弹尾部位为Φ=180°，再次返回朝头部方向为Φ=360°。

图8 水平舵轴热环境计算与试验结果对比Fig.8 Comparison between calculation heatflux and test results of horizontal rudder shaft

可以看出，计算结果与试验结果吻合较好，很好地模拟出了舵轴一周的热流分布规律。舵轴表面热流峰值出现在约Φ=20°位置，这是由于存在20°的迎角，之后热流迅速下降，在舵轴背风面（Φ=200°附近）热流非常低，整体上呈现在峰值两侧对称分布。证明了本文采用的数值计算方法在模拟舵轴热环境方面具有较高的可信度。

2 不同工况舵轴热环境分布规律

为了对舵轴热环境随马赫数、高度、迎角、舵偏角的变化规律进行研究，选取马赫数5～15、高度10～50 km、迎角0°～40°、舵偏角-10°～10°情况下的240 个组合典型状态，计算得到了舵轴位置热环境分布特征，具体计算状态如表1 所示，其中舵偏角的定义为从模型尾部向前看，控制舵顺时针偏转为正舵偏，控制舵逆时针偏转为负舵偏。由于所有工况均为飞行条件，故在开展计算时，来流湍流度均设置为0.2‰。

表1 计算状态表Table 1 Typical flow field

图9～11 分别是马赫5、高度20 km、15°迎角条件下迎风舵、水平舵、背风舵附近的流场及物面压力分布云图。从图9（a）可以看到，由于模型头部弓形激波与舵本身产生的激波相互干扰，进而导致迎风舵前缘压力的明显上升。且从图9（b）中可以看到，模型前体气流沿流向进入缝隙后，在空气舵和模型基体形成的受限空间内由于局部强压缩效应，导致舵轴前缘及缝隙中的压力值依然处于较高水平。

图9 迎风舵附近局部流场压力分布Fig.9 Pressure contour of the windward rudder

从图10 可以看到，在有迎角条件下，相对迎风舵，头部弓形激波对水平舵产生的干扰相对较弱。特别值得指出的是，由于气流对水平舵面两侧的干扰程度不同，进而导致水平舵下表面的压力值明显高于上表面。且由于上下表面气流的压差，造成下表面气流上洗，对舵轴产生强烈冲击效应。

图10 水平舵附近局部流场压力分布Fig.10 Pressure contour of the horizontal rudder

从图11 可以看到，由于该舵处于背风区，头部激波由于激波角较大，不会与该舵产生激波干扰，基本对舵体无影响，舵轴局部压力值也处于极低水平。

图11 背风舵局部流场压力分布Fig.11 Pressure contour of the leeward rudder

为直观了解该飞行器控制舵及对应舵轴区域气动热环境分布特征，图12 给出迎风舵、水平舵、背风舵及其舵轴上的热流分布。可以看出，对于控制舵表面的热流分布规律与压力基本完全相同，在15°迎角条件下，迎风舵热流最高，水平舵次之，背风舵最低。但是对于舵轴峰值热流，水平舵最高，迎风舵次之，背风舵最低。这是由于有迎角时水平舵轴受到下表面气流的上洗作用，舵面两侧压力差异较大，高温气流受迫从舵轴附近的缝隙泄流，造成热流明显上升。而迎风舵轴，虽然所处位置压力较大、舵面热环境严酷，但舵轴位于边界层底层，且舵面两侧压力基本相当，直接作用于舵轴上的气流能量相对水平舵更低，进而导致热流值也相对较小。背风舵轴位置压力较小、热环境缓和，且基本无泄流发生，因此热环境最为缓和。

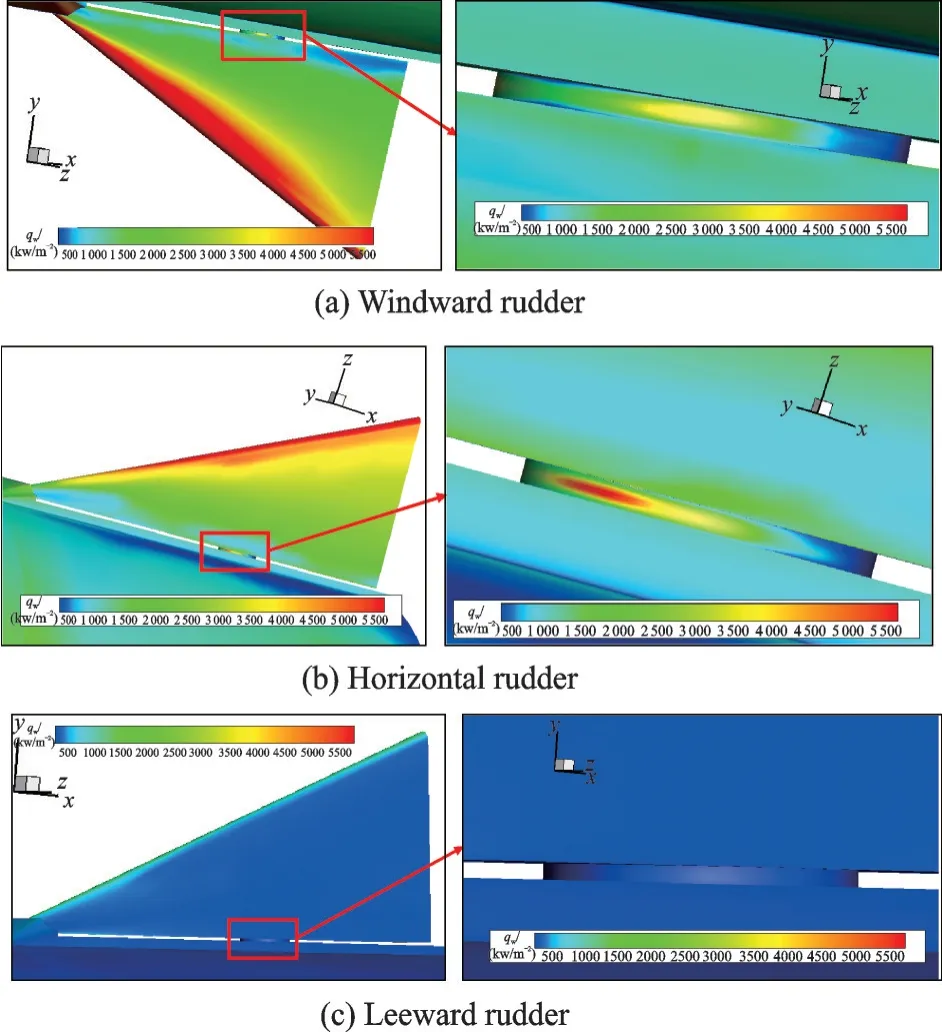
图12 舵面及舵轴热流分布规律Fig.12 Heatflux distribution of the rudder surface and rudder shaft

因此，本文重点针对热环境最为严酷的水平舵轴，分析迎角、舵偏角、马赫数等因素的影响规律。

2.1 迎角对热环境的影响分析

由于不同工况下，舵轴的热流量值相差较大，为了便于对比，本文采用以弹体迎风子午线相应位置的热流为参考值，对舵轴峰值热流进行无量纲化处理。本文首先在高度H=20 km、来流马赫数Ma∞=5 条件下，分析水平舵轴上的峰值热流随迎角和舵偏角的变化规律，如图13 所示，图中的每个点表示一个状态的计算结果。

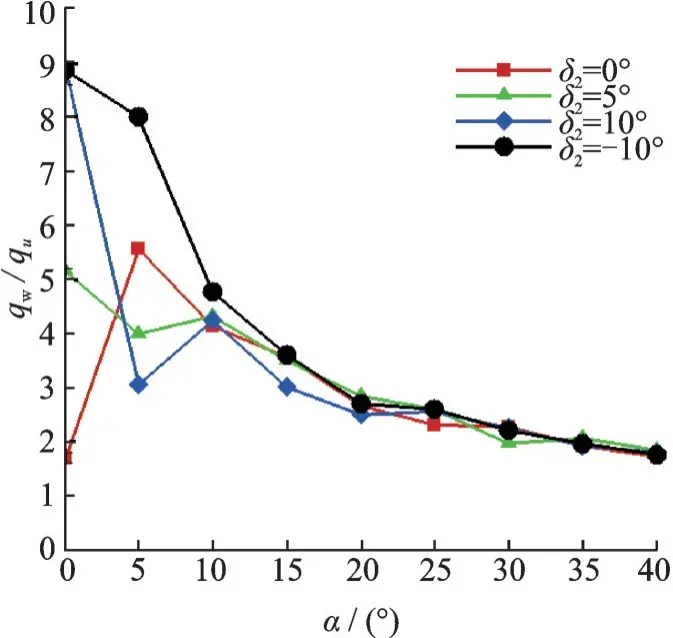
图13 高度H=20 km、马赫5、不同舵偏峰值热流随迎角变化规律Fig.13 Variation of peak heatflux of different rudders with angle of attack(H=20 km, Ma=5)

从计算结果中可以看到，在0°迎角情况下，水平舵在0°舵偏条件下的热流峰值最低，这是由于0°迎角0°舵偏情况下，舵的前半部分对舵轴起到了遮挡作用；随着舵偏角的增大，遮挡效应减弱，热流值逐渐上升；同时可以看出，当舵偏δ=10°和δ=-10°时，由于流场结构完全对称，故舵轴热流峰值也一致。

当来流迎角增加至5°时，舵偏角δ=-10°时对应的舵轴峰值热流最高，0°舵偏热流次之，随舵偏角的增大，热流下降。这是由于负舵偏时气流直接作用于舵轴，导致舵轴热流高于相应迎角条件下的正舵偏对应的舵轴热流。当来流迎角进一步增大时，舵轴上的无量纲热流峰值呈迅速下降。但当迎角大于10°迎角后，舵偏角对无量纲热流的影响较小。分析原因在于，在大迎角条件下，由于气流上洗作用导致的气动加热效应明显强于舵面偏转带来的影响。

2.2 马赫数对热环境的影响分析

本文进一步固定高度H=20 km，通过改变来流马赫数Ma∞=5、10、15，分析迎角和舵偏角对水平舵轴上的峰值热流的影响规律。

从图14 可以清楚地看出，在来流马赫数Ma∞=10、15 条件下，舵轴无量纲峰值热流随舵偏及迎角的变化规律与来流马赫数Ma∞=5 条件下的结果（图13）类似。同时，本文发现随着来流马赫数增大，在相同舵偏角条件下，迎角α=0°情况下无量纲热流呈上升趋势，大迎角情况下反而呈下降趋势。且在大迎角条件下，马赫数和舵偏对舵轴无量纲热流的影响均减小。

图14 高度H=20 km、不同马赫数、不同舵偏峰值热流随迎角变化规律Fig.14 Variation of peak heatflux of different rudders with angle of attack at different Mach numbers(H=20 km)

3 舵轴热环境关联分析

在分析舵轴无量纲峰值热流随迎角、舵偏角及马赫数变化规律的基础上，本文以迎风舵前无干扰热流值为无量纲参考值的无量纲热流作为拟合对象，建立了以高度、马赫数、迎角和舵偏角为参数的插值拟合方法，通过该方法可以在给定的工况条件下，考虑高度、马赫数、迎角以及舵偏角的影响，通过线性插值以获得该工况下舵轴热环境。

具体拟合公式为

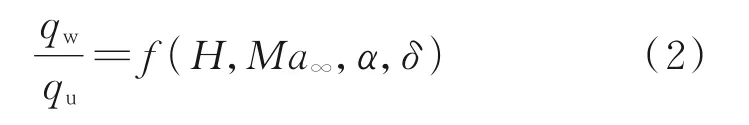
本文首先采用该拟合公式在高度H=15 km条件下，针对迎角α=0°、3°、6°、9°、12°、15°六个不同状态开展了估算，并将估算结果与采用数值求解N-S 方程模拟方法在高度H=10 km、20 km 条件下的结果开展了对比分析，如图15 所示。可以看出，在6 个不同迎角条件下，采用关联公式得到插值结果处于高度H=10 km、20 km 对应迎角的数值计算结果包络范围内。这说明，本文建立的数据拟合方法具有一定可行性。

图15 15 km 舵轴峰值热流拟合结果与高度包络对比Fig.15 Comparison of peak heatflux fitting results and the CFD results at 15 km

为了进一步验证式（2）在不同高度条件下舵轴热流拟合的适用性。本文继续针对高度H=45 km 条件下的无量纲热流数据进行了拟合，并将拟合结果与高度H=30 和50 km 条件下的数值计算结果开展了对比分析（图16）。结果表明，本文建立的方法可以通过有限的数据插值获得各个高度下舵轴的热流峰值，从而可以实现沿弹道对机动再入飞行器舵轴热环境开展估算，且具有一定通用性。

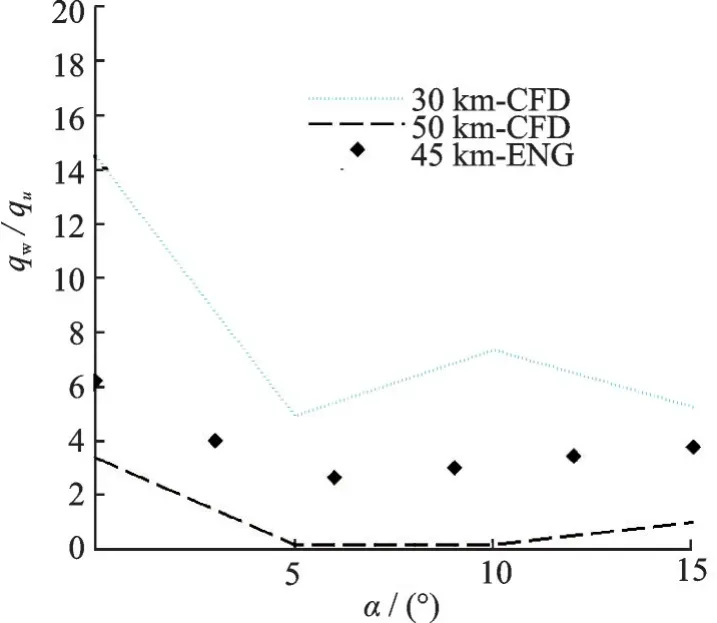
图16 45 km 舵轴峰值热流拟合结果与高度包络对比Fig.16 Comparison of peak heatflux fitting results and the CFD results at 45 km

4 结 论

本文采用数值模拟方法和地面风洞试验方法，针对舵轴热环境开展了影响参数研究，初步得到了高度、迎角、舵偏角对舵轴局部热环境的影响规律，并建立了以高度、马赫数、迎角和舵偏角为参数的舵轴热环境工程关联方法。通过研究，可以得出以下结论：

（1）试验和计算结果均表明，舵轴表面及其干扰区的峰值热流是非常高的，必须在飞行器设计阶段引起足够的重视。

（2）对于本文研究的十字布局弹头，大迎角时由于气流上洗作用，水平舵轴热环境最为恶劣，其次是迎风舵轴，背风舵轴热环境较为缓和。

（3）通过对不同工况下舵轴附近流场结构及物面载荷的数值计算结果分析，初步获得了舵轴热环境峰值随马赫数、迎角、舵偏角等的变化规律，分析表明，在小迎角条件下，水平舵轴的无量纲热流随舵偏角和马赫数逐渐上升，但在大迎角情况下，马赫数和舵偏对舵轴无量纲热流的影响较小。

（4）本文初步建立了考虑高度、迎角、马赫数和舵偏角影响效应的舵轴峰值热流插值方法，且与数值计算结果对比表明，该方法在一定范围内可对飞行工况下的舵轴热环境进行预测，且具有一定通用性，可以在工程先期设计中，实现对舵轴热环境沿飞行历程的快速预测。