基于蒙特卡洛的飞机控制分配鲁棒性评估方法

王晓光，尚永爽，杜 军，贾文铜，史静平，吕永玺

(1.空军工程大学航空工程学院，陕西 西安 710038；2.中国人民解放军93184部队，北京 100076；3.西北工业大学自动化学院，陕西 西安 710072)

0 引言

随着现代飞行器设计对于机动性、安全性和可靠性要求的不断提高，越来越多的飞机舵面可作为主操纵系统的控制面控制飞机的运动[1-2]。对于给定的期望三轴力矩，多操纵面飞机可以有多种组合偏转形式实现相同的控制目标，针对具有多操纵面配置的飞行器开展多操纵面控制分配技术的研究成为一种必然。

多操纵面布局飞机的控制问题本质上是一个多目标优化问题，如巡航阻力最小、起飞升力最大等[3-4]。目前可用于线性过驱动系统控制分配优化求解的方法可归纳为三类[5-6]：一是广义逆类分配方法，主要包括：伪逆法、加权伪逆法、再分配伪逆法、多级伪逆法等；二是几何类分配方法，主要包括：串接链法、直接分配法和对边搜索法等；三是数学规划类方法，包括：面搜索法、不动点迭代法、有效集法、基于频域加权的二次规划法等。

鲁棒性是反映控制系统性能优劣的重要指标[7]。为评估不同控制分配方案的优劣，国内外学者经常将系统的鲁棒性作为指标来进行控制分配的效果评估。文献[8]从控制系统鲁棒性角度出发，针对多操纵面飞机气动效能的交叉耦合不确定性，提出了一种基于混合优化的鲁棒控制分配策略，建立了鲁棒混合优化控制分配模型。文献[9]针对具有冗余执行机构的过驱动系统，在考虑控制效率不确定性的条件下，提出了一种基于鲁棒优化理论的控制分配算法，有效降低了控制效率不确定性的影响，使分配结果更为合理，一定程度上提高了控制分配算法的鲁棒性，改善了飞控系统的性能。文献[10]基于广义逆控制的飞控系统，分析了控制系统的不确定性以及在控制效能矩阵存在不确定性时的飞控系统鲁棒性问题。文献[11]针对一类具有不确定时变参量的线性参变过驱动系统的控制分配问题，考虑系统的不确定参量扰动和执行器物理约束，建立了含有时变不确定因子的控制分配优化模型，并根据鲁棒优化思想，采用矢量变换技术处理时变不确定因子，得到了一种基于有约束锥二次凸优化模型的鲁棒控制分配算法，实现对过驱动系统伪控指令的在线优化分配。文献[12]针对无人机广泛采用先进操纵面带来的控制分配问题，提出了基于闭环广义逆的鲁棒控制分配新方案，在基于广义逆的控制分配方法基础上，加入了控制量对应状态的反馈，分析了该方案的可行性。同时，鲁棒控制分配方法也在国内外航天、航海等其他领域有所应用[13-15]。

然而，上述文献均是针对不同的控制分配方法，从不同的角度出发评估某一特定控制分配方法的鲁棒性，很难适用于其他控制分配方法。因此，有必要构建一种通用的多操纵面飞机控制分配鲁棒性评估方法，为过驱动系统的控制分配效果提供较为统一的评价准则。基于此思路，本文给出了一种通用的基于蒙特卡洛方法的控制分配鲁棒性评估框架；建立了过驱动系统的控制分配方法鲁棒性评估函数；对伪逆法、串接链法和面搜索法三种典型的分配方法进行了仿真验证，并给出了结论。

1 鲁棒性评估思路和框架

对飞机飞行品质的评估是基于飞机飞行控制律进行的，评估需考虑的不确定性包括：质量数据的不确定性、系统输入量的不确定性、气动数据库的不确定性等。其一般实现过程：在考虑上述不确定性的情况下，设计出控制律之后，通过随机模拟的方法对飞机的一些特征量(气流角、位置、被控量的调节时间和超调量等)进行统计分析，来获得控制律在不确定参数下鲁棒性能的量化值。但过驱系统分配方法鲁棒性的研究，有别于已有控制律的飞行品质评估[16]。由于过驱系统的设计目的是将期望的三轴力矩系数合理地分配到各个舵面，因此在研究过驱系统的参数不确定时只需考虑舵面效率的不确定性。对于线性过驱系统分配方法的鲁棒性研究是基于控制效能矩阵中参数的不确定性。

本文针对过驱系统分配方法进行鲁棒性评估的基本思想：考虑舵面效率的不确定性范围，根据鲁棒性要求的精度和置信度确定最小仿真次数；基于蒙特卡洛方法[17]进行随机模拟仿真获得实际三轴力矩系数，建立过驱系统分配方法鲁棒性的评估函数；针对不同的分配方法求得鲁棒性能量化值，进而可以比较分析各个方法鲁棒性的优劣。

进行过驱系统分配方法鲁棒性评估的具体步骤如下：

1) 确定控制效能矩阵中参数的不确定性范围；

2) 由给定精度和置信因子确定最小仿真次数，并且产生满足分布的控制效能矩阵参数的随机数；

3) 建立过驱系统分配方法鲁棒性评估指标函数；

4) 进行多次仿真，获得仿真结果后进行参数概率统计分析，依据鲁棒性评估指标函数验证控制分配算法的鲁棒性；

5) 比较不同控制分配方法的鲁棒性，为控制分配方法的选择提供依据。

过驱系统分配方法的鲁棒性研究验证过程如图1所示。

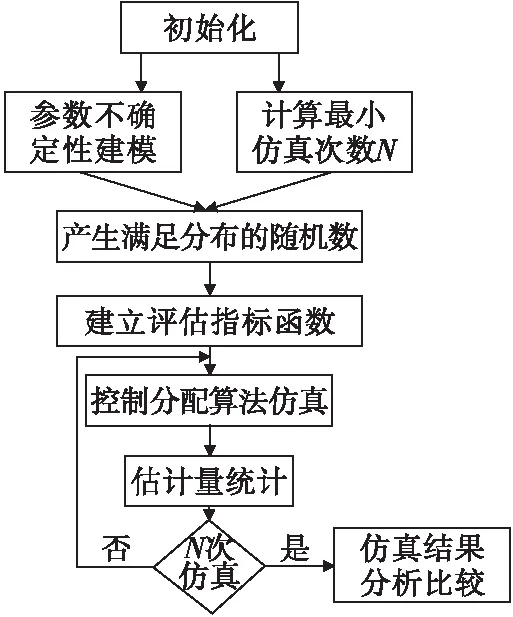
图1 基于蒙特卡洛的过驱系统分配方法鲁棒性验证框图Fig.1 Robustness verification diagram of overdrive system’s control allocation method based on Monte-Carlo

2 过驱系统分配方法鲁棒性评估指标函数

2.1 相关概率统计基础

2.1.1 3σ原则

对于分布为N(μ,σ2)的随机变量x，数值分布在(μ-3σ,μ+3σ)中的概率为0.997 3，可以认为正态随机变量的取值在(μ-3σ,μ+3σ)区间内，这就是所谓的3σ原则。在参数不确定性建模时，采用3σ原则能保证构成参数不确定项的随机变量基本可以限定在3σ分布范围内，从而避免因为参数值出界而导致的系统不稳定。

2.1.2 最小仿真次数确定方法

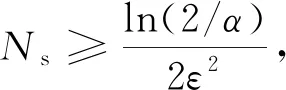
2.1.3 均值和方差的估计值计算

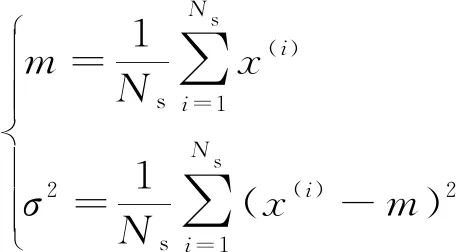
(1)

当样本数量足够多时，样本均值的置信区间为：

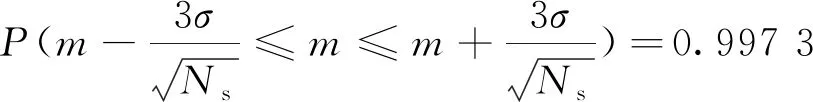
(2)

2.2 鲁棒性评估指标函数的建立

过驱系统分配方法的实质是按照一定的指标要求将期望的三轴力矩系数合理地分配到各个舵面上去，其最基本的要求是分配系统的实际三轴力矩系数能够跟踪上期望的三轴力矩系数，如图2所示。

图2 分配系统的基本框图Fig.2 Basic block diagram of the allocation system

对于过驱系统分配方法鲁棒性的评估也是针对实际三轴力矩系数和期望三轴力矩系数之间的差别来入手。对于给定的三轴期望力矩系数，在控制效能矩阵参数存在不确定性的情况下进行N次仿真后，可求出实际三轴力矩系数的均值和方差值，并且可以确定均值相应的置信区间，根据这些统计信息便可以评估在给定的三轴期望力矩系数下分配方法的鲁棒能力。

具体在仿真验证过程中，采取下式所示的性能评估函数

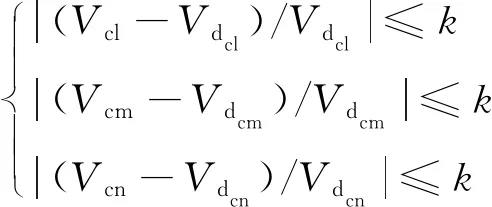
(3)

式(3)中，Vcl、Vcm、Vcn分别为实际的滚转力矩系数、实际的俯仰力矩系数和实际的偏航力矩系数；Vdcl、Vdcm、Vdcn分别为期望的滚转力矩系数、期望的俯仰力矩系数和期望的偏航力矩系数；k是评估指标系数，是一个无量纲量，它反映了评估函数对实际输出的力矩系数和期望的力矩系数二者之间的差别要求。k的选用原则是结合飞机舵面效率的不确定性，以尽可能清晰、准确地体现控制分配方法的鲁棒性。如果指定了k的值，则可以在仿真中记录满足性能评估标准要求的次数n，显然，0≤n≤N。n的大小代表了在评估指标系数k下分配方法的鲁棒性，n值越大则说明在评估指标系数k下该分配方法的鲁棒性越强，反之亦然。因此控制分配方法鲁棒性的优劣还可以表现在累积频数曲线中。

3 鲁棒性验证

一般来说，线性过驱动系统可描述为：假设控制变量为u(t)∈Rm1，期望的虚拟变量是v(t)∈Rm2，线性过驱动系统的分配问题就是在给定v(t)及映射Be:Rm1→Rm2(m1>m2)的情况下，求解不定方程Beu(t)=v(t)，使u(t)在不超出约束Ω的情况满足一定的性能指标。

从数学描述上看，线性过驱动系统的分配求解问题是一个受约束的线性方程组求解问题，由于控制变量的维数大于虚拟变量的维数，分配问题的解有三种情况：多解、唯一解、无解。从数学映射关系上分析，线性过驱动系统的分配问题求解是根据映射Be:Rm1→Rm2(m1>m2)找到一种反映射，使解不超出约束；并且这种反映射还可能包含其他系统性能指标。这些指标在保证等式约束Beu(t)=v(t)的同时，还使线性过驱动系统的分配求解与工程设计的需求相匹配。

以Admire多操纵面飞机为例，在马赫数为0.4，高度为3 000 m的状态点下得到控制效能矩阵：

将Be作为标称效能阵，同时选取精度ε=0.05，置信因子α=0.04，结合最小仿真次数的计算公式，得到最小仿真次数Ns≥782.4，故可取仿真次数N=800，对于控制效能矩阵中的任意参数bij，设定每个舵面舵效值的不确定性为50%。在此基础上进行控制分配方法鲁棒性评估验证，评估验证过程中涉及控制分配方法的具体步骤详见文献[18]。

3.1 伪逆分配方法的鲁棒性评估

给定期望的三轴力矩系数：

vd=[0.03 0.3 -0.03]。

(4)

进行N次蒙特卡洛仿真后得到伪逆法对应的实际无量纲三轴力矩系数曲线如图3所示。

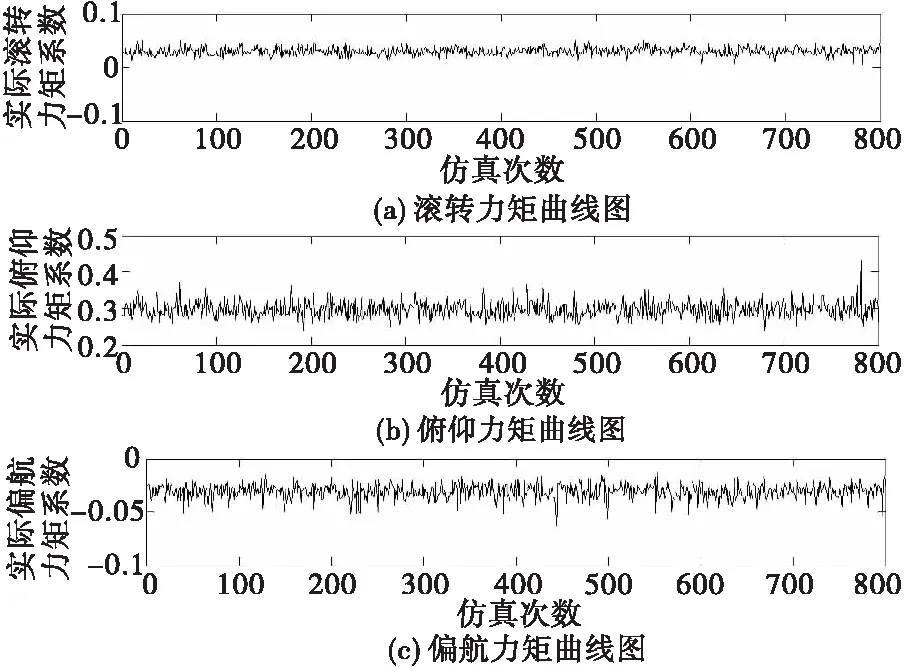
图3 控制效能矩阵不确定时的伪逆法三轴力矩系数Fig.3 Triaxial torque coefficients of pseudo inverse method for uncertain control efficiency matrix

统计得到实际三轴力矩系数的均值与标准差，并求其对应的样本均值置信区间，结果如表1所示。

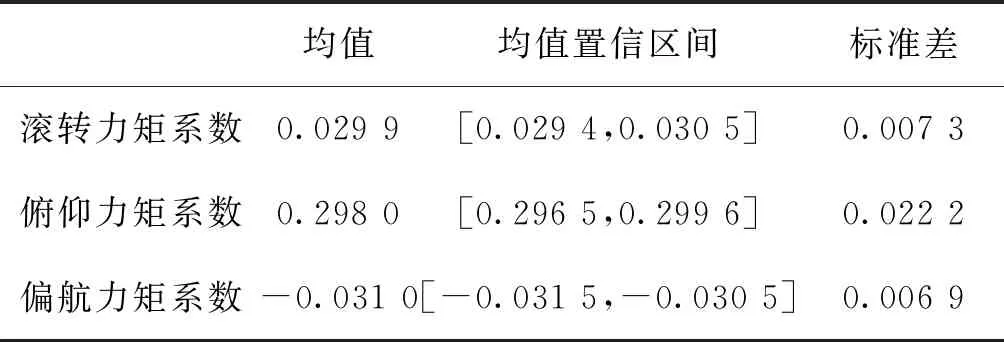
表1 伪逆法仿真结果统计Tab.1 Simulation result statistics for pseudo inverse method

结合图3和表1来看，在舵面效率存在50%的不确定性时，通过蒙特卡洛仿真验证可知，实际的三轴力矩系数均在期望三轴力矩系数附近，伪逆法对于舵效的不确定性具有一定的鲁棒性。

伪逆分配法考虑控制效能矩阵不确定时的累积频数曲线如图4所示。

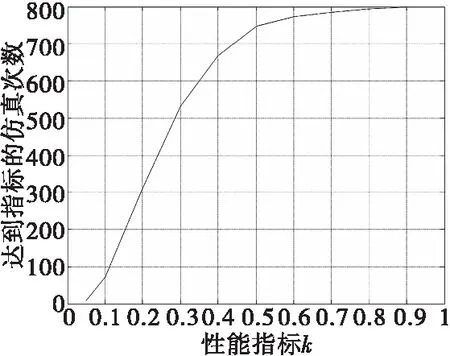
图4 控制效能矩阵不确定时的伪逆法累积频数曲线Fig.4 Frequency accumulating curve of pseudo inverse method for uncertain control efficiency matrix

考虑舵效值的50%不确定性，结合图4可知，当评估指标系数k=0.5时，达到指标的仿真次数为752，也就是说此期望状态下对于控制效能矩阵参数的不确定性，伪逆法得到的实际三轴力矩系数值与期望三轴力矩系数之差有94%的概率不超过期望三轴力矩系数的一半。

3.2 串接链分配方法的鲁棒性评估

给定期望的三轴力矩系数vd不变，进行N次蒙特卡洛仿真后得到串接链法对应的实际无量纲三轴力矩系数曲线如图5所示。

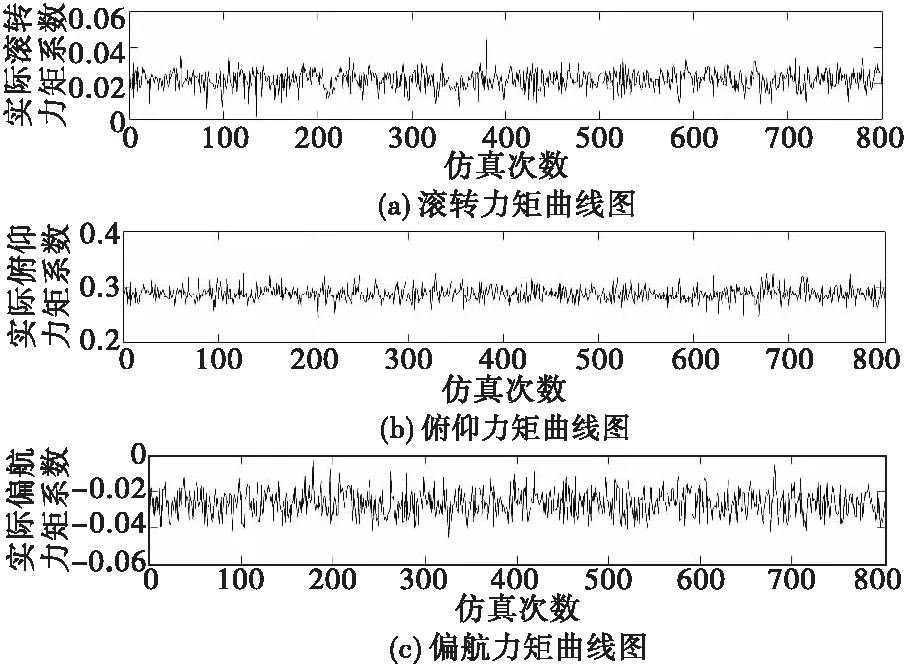
图5 控制效能矩阵不确定时的串接链法三轴力矩系数Fig.5 Triaxial torque coefficients of daisy chain method for uncertain control efficiency matrix

统计N次蒙特卡洛仿真后实际三轴力矩系数的均值与标准差，求得其对应的均值置信区间，如表2所示。

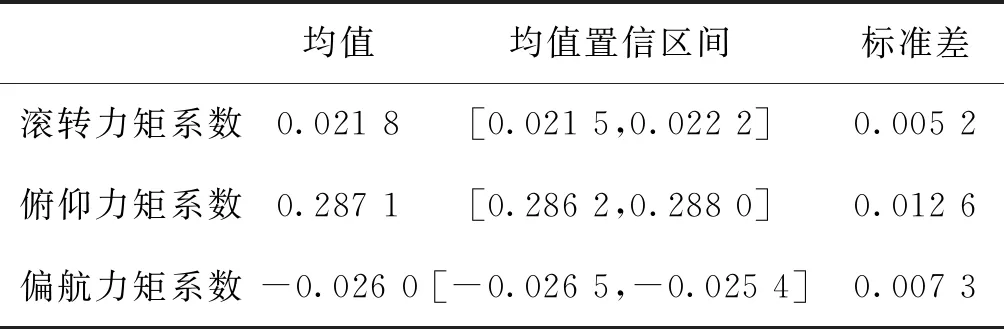
表2 串接链法仿真结果统计Tab.2 Simulation result statistics for daisy chain method

结合图5和表2中数据来看，在舵面效率存在50%的不确定性时，同伪逆法相比，串接链法均值离期望力矩系数较远，且期望的三轴力矩系数在均值置信区间之外，说明仿真得到的力矩系数与期望力矩系数差别较大；标准差总体上比伪逆法大，说明仿真结果分布较为分散。因此，从仿真统计结果分析，可以认为该方法在舵面效率存在50%的不确定性时鲁棒性比伪逆法差。

串接链分配方法考虑控制效能矩阵不确定时的累积频数曲线如图6所示。

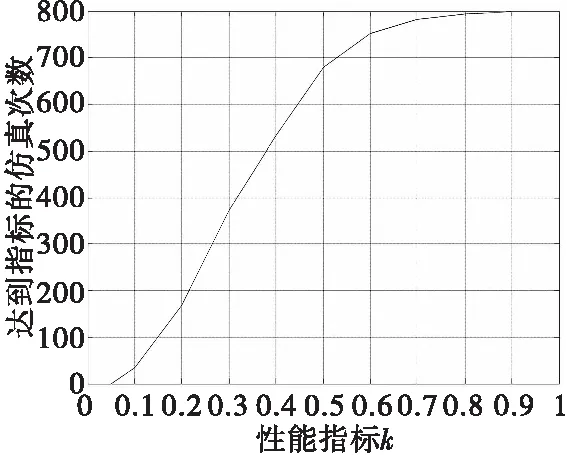
图6 控制效能矩阵不确定时的串接链法累积频数曲线Fig.6 Frequency accumulating curve of daisy chain method for uncertain control efficiency matrix

考虑舵效值的50%不确定性，结合图6可知，当k=0.5时，此期望状态下对于所有的控制效能矩阵参数的不确定性，串接链法达到指标的仿真次数为679，也就是说此期望状态点下对于控制效能矩阵参数的不确定性，串接链法得到的实际三轴力矩系数值与期望三轴力矩系数之差有84.88%的概率不超过期望三轴力矩系数的一半。总体来说，串接链法对于舵效不确定性的鲁棒性比伪逆法差。

3.3 面搜索分配方法的鲁棒性评估

给定期望的三轴力矩系数vd不变。进行N次蒙特卡洛仿真后得到面搜索法对应的实际无量纲三轴力矩系数曲线如图7所示。

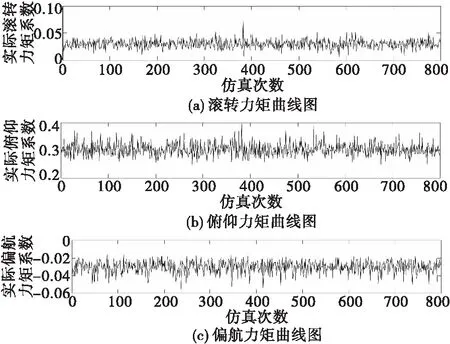
图7 控制效能矩阵不确定时的面搜索法三轴力矩系数Fig.7 Triaxial torque coefficients of surface search method for uncertain control efficiency matrix

统计N次蒙特卡洛仿真后实际三轴力矩系数的均值与标准差，并求其对应的均值置信区间如表3所示。

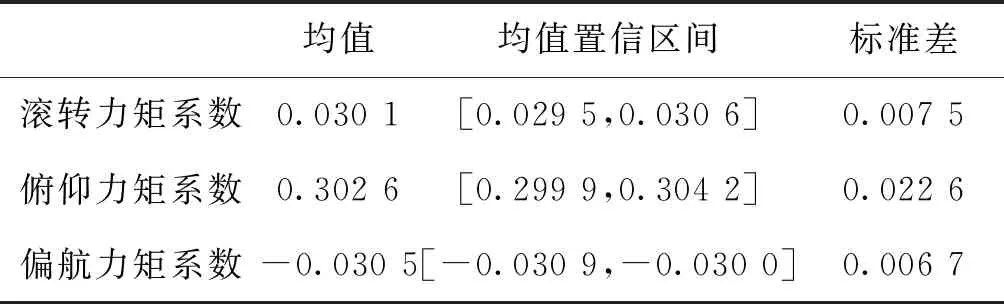
表3 面搜索法仿真结果统计Tab.3 Simulation result statistics for surface search method

结合图7和表3来看，在舵面效率存在50%的不确定性时，通过蒙特卡洛仿真验证可知，面搜索法计算得到的三轴力矩系数均值在期望三轴力矩系数附近，且期望的三轴力矩系数均在均值置信区间之内，说明面搜索法仿真得到的力矩系数与期望力矩系数差别不大，面搜索法对于舵效的不确定性具有一定的鲁棒性。但该方法的仿真结果统计中标准差总体上稍大，说明该方法的仿真结果分布较散。

考虑控制效能矩阵不确定时的累积频数曲线如图8所示。

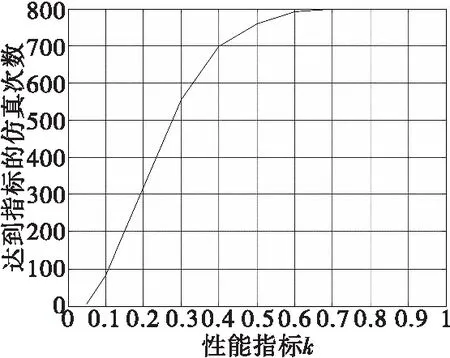
图8 控制效能矩阵不确定时的面搜索法累积频数曲线Fig.8 Frequency accumulating curve of surface search method for uncertain control efficiency matrix

考虑舵效值的50%不确定性，结合图8可知，k=0.5时，此期望状态下对于所有的控制效能矩阵参数的不确定性，面搜索法达到指标的仿真次数为758，也就是说此期望状态点下对于控制效能矩阵参数的不确定性，面搜索法得到的实际三轴力矩系数值与期望三轴力矩系数之差有94.75%的概率不超过期望三轴力矩系数的一半，优于伪逆法和串接链法。

总体来说，通过综合对比仿真结果统计和累积频数曲线可以发现：与前两种方法相比较，面搜索方法的鲁棒性最强。究其原因在于面搜索法的分配效率最高，在分配时能够最大限度达到转矩可达集边界，进而当控制效能矩阵存在不确定时能够体现较强的鲁棒性。

4 结论

本文提出一种多操纵面飞机控制分配的鲁棒性评估方法，在建立鲁棒性评估指标函数的基础上，基于蒙特卡洛方法，进行了数值计算仿真，对伪逆、串接链和面搜索三种控制分配方法进行了鲁棒性评估。仿真结果表明，该方法可以有效实现控制分配方法的鲁棒性评估，具有较好的通用性和较高的评估准确度，能够为控制分配的性能评估提供有效的技术支撑和参考。仿真结果显示，在控制效能矩阵存在50%不确定性的情形下，面搜索法的鲁棒性能最好，伪逆法次之，串接链法的鲁棒性能最差。