考虑纤维角度变化的各向异性材料柔顺机构拓扑优化设计

占金青,秦洋洋,刘敏

(华东交通大学 机电与车辆工程学院,南昌 330013)

柔顺机构是利用其柔性部件或机构整体的弹性变形将力、运动和能量从输入端传递到输出端的一种机构[1-3]。与传统的刚性机构比较,柔顺机构具有结构简单、无摩擦、重量轻、易加工、精度高等优点。因此,柔顺机构在航空航天、微机电系统、医疗器械、精密定位操作等领域中具有广阔的应用前景[4-6]。

目前,柔顺机构拓扑优化设计研究大多采用单一材料设计[7-10],然而单一材料柔顺机构表现出变形与承载的局限性。与各向同性材料相比,复合材料具有独特的各向异性特性,这为柔顺机构克服以上不足提供一种有效途径[11]。梁森等[12]在给定层合纤维方向下,采用水平集方法进行复合材料层合结构拓扑设计。Li等[13]基于经典层合板理论推导平面应力问题的层合板本构关系,建立各向异性材料柔顺机构拓扑优化模型,进行单输入多输出柔顺机构设计。Tong等[14]考虑给定层合纤维方向的前提下,进行常刚度层合板的柔顺机构拓扑优化设计,分析不同层合板每层的固定纤维方向对拓扑构型、变形能力和应力的影响。Tong等[15]提出以层合参数和单元相对密度为设计变量的常刚度层合板纤维方向与拓扑联合优化数学模型,实现了机构构型和层合纤维方向的联合优化设计,但是每层所有的设计单元的纤维角度都是一样的,没有进行单层的纤维角度优化。在此基础上,将该方法进行柔性机翼前后缘层合板纤维方向与构型设计[16]。综上所述,现有的各向异性材料柔顺机构拓扑优化设计研究主要考虑固定纤维角度的情况,没有进行设计单元的纤维角度优化。

本文提出一种考虑纤维角度变化的各向异性材料柔顺机构拓扑优化设计方法。采用改进的固体各向异性材料惩罚模型引入变化的设计单元纤维角度,以柔顺机构的互应变能最大化为目标函数,以材料体积为约束,建立考虑纤维角度变化的各向异性材料柔顺机构拓扑优化数学模型,采用移动渐近算法求解各向异性材料柔顺机构拓扑优化问题。

1 各向异性柔顺机构拓扑优化模型

1.1 正交各向异性材料的弹性特征

由正交各向异性理论,在纤维主方向坐标系中,二维正交各向异性材料弹性矩阵C可表示为[17]

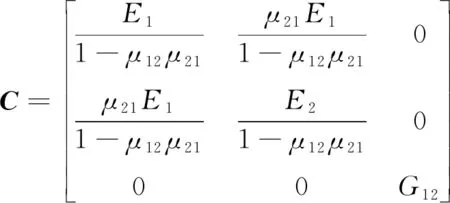
(1)

式中:G12为材料的剪切模量;E1、E2、μ12、μ21分别代表单层材料的纵向模量、横向模量、纵向泊松比和横向泊松比,4个材料参数存在以下关系

(2)

当纤维主方向局部坐标系和全局坐标系存在相对转动θ,局部坐标下的应力σ和全局坐标下的应力σ′之间关系可表示为

(3)

式中:σx和σy分别为局部坐标系下的x和y方向的应力;τxy为局部坐标系下的剪切应力;σ′x和σ′y分别为全局坐标系下的x′和y′方向的应力;τ′xy为全局坐标系下的剪切应力。

式(3)可改写为

σ=T·σ′

(4)

式中T为转换矩阵。

局部坐标下的应变ε和全局坐标下的应变ε′之间关系可表示为

(5)

式中:εx、εy和εxy为局部坐标下的应变;ε′x、ε′y和ε′xy为全局坐标系下的应变。

其中

(6)

式(5)进一步可改写为

ε=RTR-1ε′

(7)

在平面应力状态下,正交各向异性材料的本构方程为

σ=Cε

(8)

由式(4)和式(7)代入式(8),可求得全局坐标下的弹性矩阵C′为

C′=T-1CT-T

(9)

1.2 改进的SOMP插值模型

传统的SOMP插值模型[11]仅将固体各向同性材料插值方法拓展到各向异性材料,分别对材料的3个弹性模量进行插值,并未考虑设计单元纤维角度变化的情况。本文考虑纤维角度变化的各向异性材料,采用改进的SOMP插值模型[18]对各向异性材料主方向的弹性模量进行惩罚

(10)

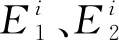
1.3 柔顺机构拓扑优化模型

为满足机构运动要求,以柔顺机构的互应变能最大化为优化目标函数,互应变能越大,表示柔顺机构的变形能力越大,并且以机构的体积为约束,采用改进的SOMP材料插值模型建立考虑纤维角度变化的各向异性材料柔顺机构拓扑优化数学模型为

(11)

2 灵敏度分析及过滤技术

2.1 灵敏度分析

移动渐近算法[19](Method of moving asymptotes, MMA)具有很好的稳定性和鲁棒性,本文采用MMA算法进行更新设计变量。

由式(11),柔顺机构的互应变能对单元密度变量的灵敏度可求得为

(12)

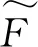
(13)

同理,柔顺机构的互应变能对单元纤维角度变量的灵敏度可求得为

(14)

其中

ke(θe)=∬BTT(θe)-1CT(θe)-TBtdxdy

(15)

充满材料的单元刚度矩阵ke对单元纤维角度变量求导,可得

(16)

式中t为设计域厚度。

由式(11),体积约束对单元密度变量的灵敏度求得为

(17)

式中ν0为充满材料单元的体积。

单元纤维角度变化不会引起材料体积改变,因此体积约束对单元纤维角度变量的灵敏度为

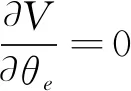
(18)

2.2 过滤技术

为了避免柔顺机构拓扑优化结果出现棋盘格和网格依赖等数值不稳定性问题,采用密度过滤方法[20]修正单元密度变量,其可表示为

(19)

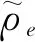
wej=max(0,rmin-de,j)

(20)

式中de,j为单元e和单元j质心之间的距离。

3 数值算例

选取夹持器和咬合机构两个数值算例来验证所提出方法的有效性。材料选取为玻璃纤维增强环氧树脂,其参数为E1=39 GPa,E2=8.4 GPa,G12=4.2 GPa,μ12=0.26,单元密度变量的初始值设置为0.4,过滤半径rmin设置为1.5;考虑纤维角度优化时,单元纤维角度变量的初始值设置为0。

3.1 夹持器

图1所示为夹持器的设计域、作用载荷、输出作用及边界条件。夹持器的设计尺寸L×L为8 mm×8 mm,厚度t=0.1 mm,设计域左边的上下两端固定,作用载荷F=0.4 N,施加在左端中点处。输入、输出端的弹簧系数均为3.5×104N/m,允许的材料体积比为0.25。由于设计域具有对称性,故选取夹持器设计域的上半部分进行优化设计,设计域离散为80×40个平面四节点单元。

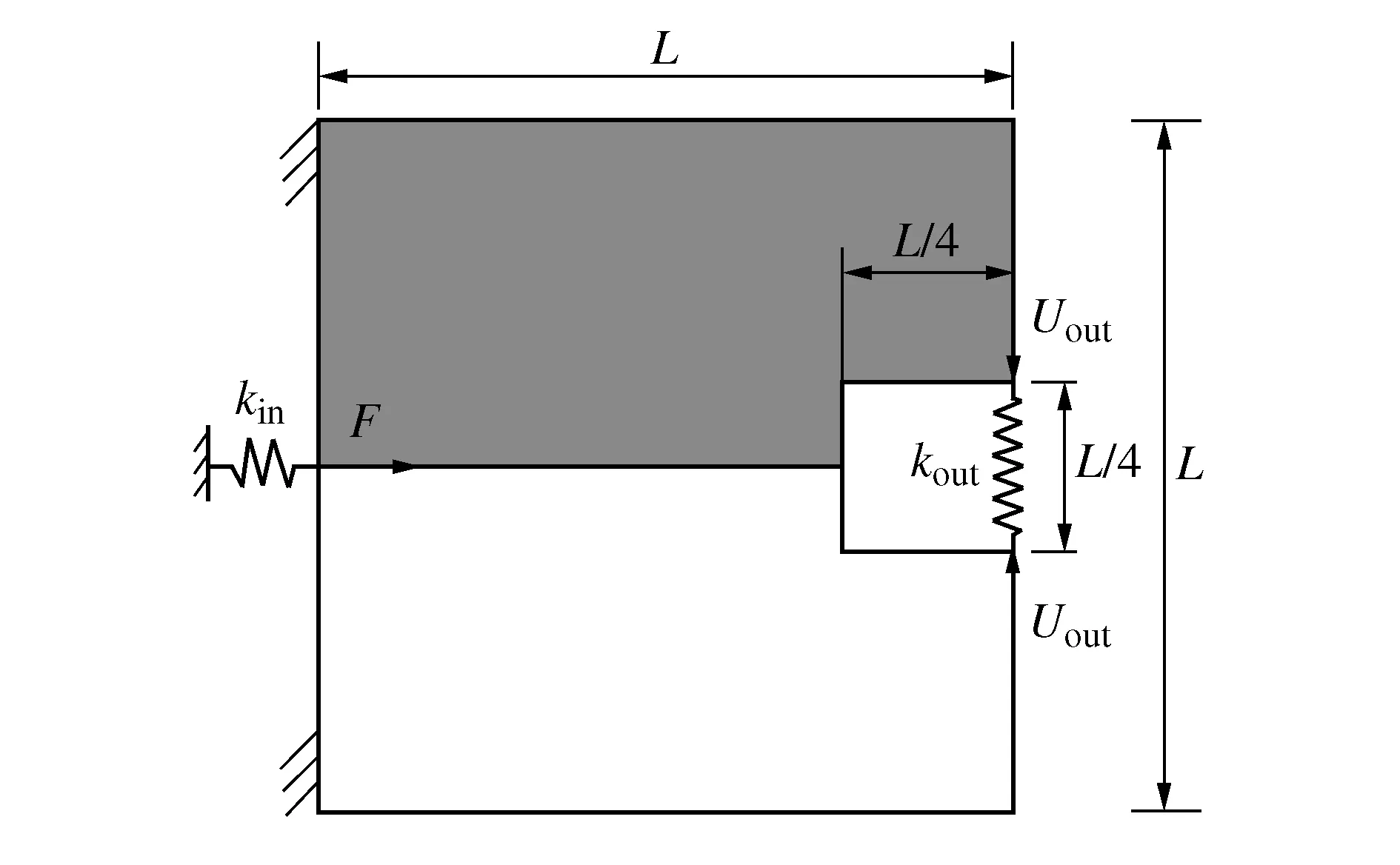
图1 夹持器设计域

为了验证所提出方法的有效性,设计参数均相同条件下将考虑纤维角度变化拓扑优化结果与固定纤维角度拓扑优化结果进行比较。首先,考虑纤维角度变化的各向异性材料夹持器拓扑优化结果如图2所示。

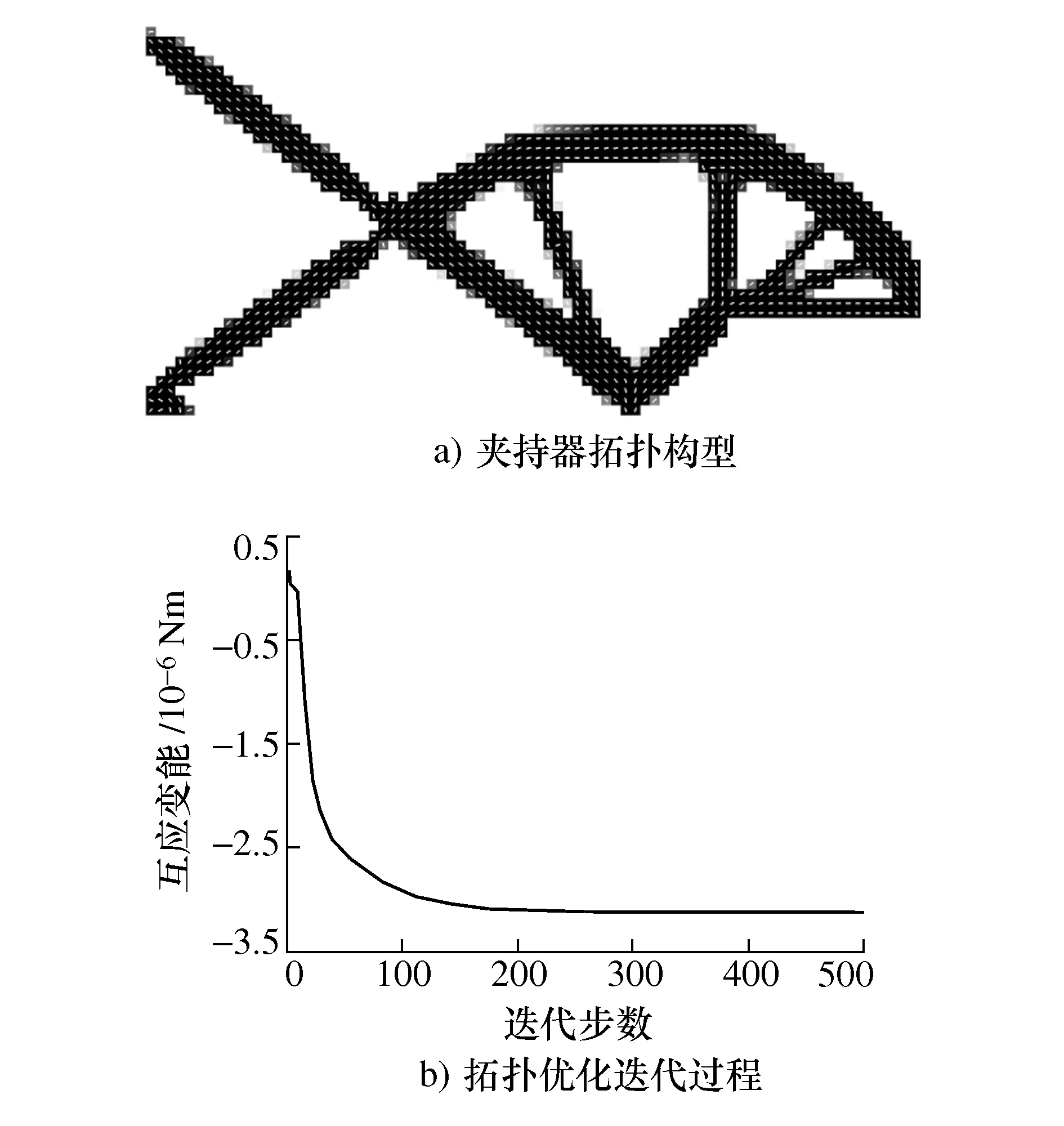
图2 考虑纤维角度变化的各向异性材料夹持器拓扑优化

由图2a)可知,考虑纤维角度变化拓扑优化获得夹持器构型中纤维角度会进行相应的调整,以使得机构的互应变能达到最大;优化目标互应变能的迭代过程中,仅当迭代到150步,迭代趋于平稳后逐渐收敛,如图2b)所示。

考虑固定纤维角度分别0、45°和90°进行各向异性材料夹持器拓扑优化设计,获得的夹持器构型和优化目标互应变能迭代图分别为如图3、图4和图5所示。3种固定纤维角度拓扑优化设计获得的夹持器构型有很大的不同;其中纤维角度固定为45°获得的夹持器的互应变能(2.153×10-6Nm)最大,如表1所示。

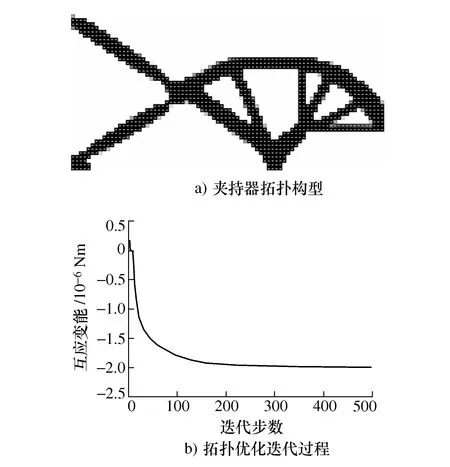
图3 纤维角度为0的各向异性材料夹持器拓扑优化

图4 纤维角度为45°的各向异性材料夹持器拓扑优化

图5 纤维角度为90°的各向异性材料夹持器拓扑优化

表1 不同纤维角度条件获得的夹持器的互应变能 Nm

与纤维角度固定拓扑优化结果相比,考虑纤维角度变化拓扑优化获得的夹持器构型有所不同,并且夹持器的互应变能(3.131×10-6Nm)也更大,为纤维角度固定为45°获得的夹持器互应变能的1.45倍,考虑纤维角度变化进行夹持器拓扑优化设计能够有效地提高夹持器的变形性能,这表明提出的设计方法是有效的。

3.2 咬合机构

图6所示为咬合机构的设计域、作用载荷、输出作用及边界条件。柔顺咬合机构的设计尺寸为8 mm×8 mm,厚度t=0.1 mm,设计域左边的上下两端固定,作用载荷F的大小为0.18 N,施加在右边上、下两端处。输入、输出端的弹簧系数均为3.0×104N/m,允许的材料体积比为0.25,由于设计域具有对称性,故选取咬合机构设计域的上半部分进行优化设计,设计域离散为80×40个平面四节点单元。

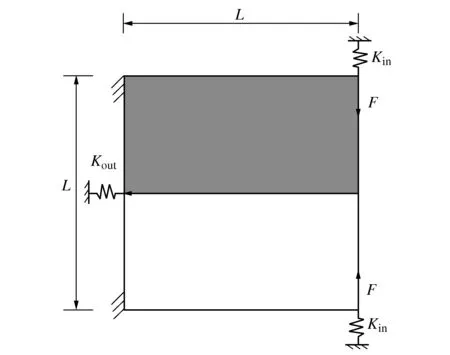
图6 咬合机构设计域

考虑纤维角度变化的各向异性材料咬合机构拓扑优化结果如图7所示。同样,考虑纤维角度变化拓扑优化获得咬合机构构型中纤维角度会进行相应的调整,以使得机构的互应变能达到最大;优化目标互应变能的迭代过程中,当迭代到75步,迭代趋于平稳后逐渐收敛,如图7b)所示。

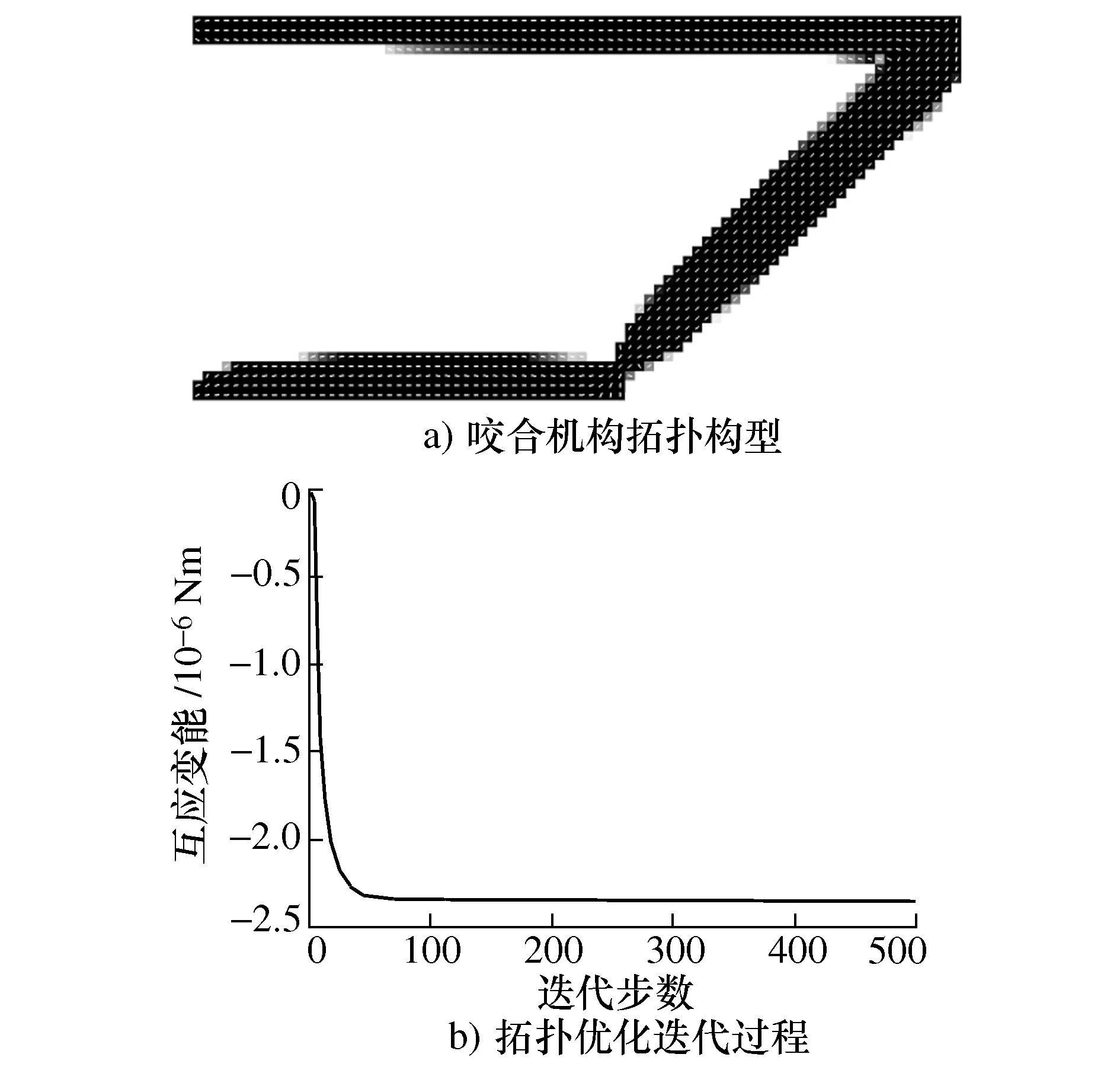
图7 考虑纤维角度变化的各向异性材料咬合机构拓扑优化

考虑纤维角度固定分别0,45°和90°进行各向异性材料咬合机构拓扑优化设计,获得的咬合机构构型和优化目标互应变能迭代图分别为如图8、图9和图10所示。3种固定纤维角度拓扑优化获得的咬合机构构型有很大的不同,其中固定纤维角度为0获得的咬合机构的互应变能(2.000×10-6Nm)最大,如表2所示。

表2 不同纤维角度条件获得的咬合机构的互应变能 Nm

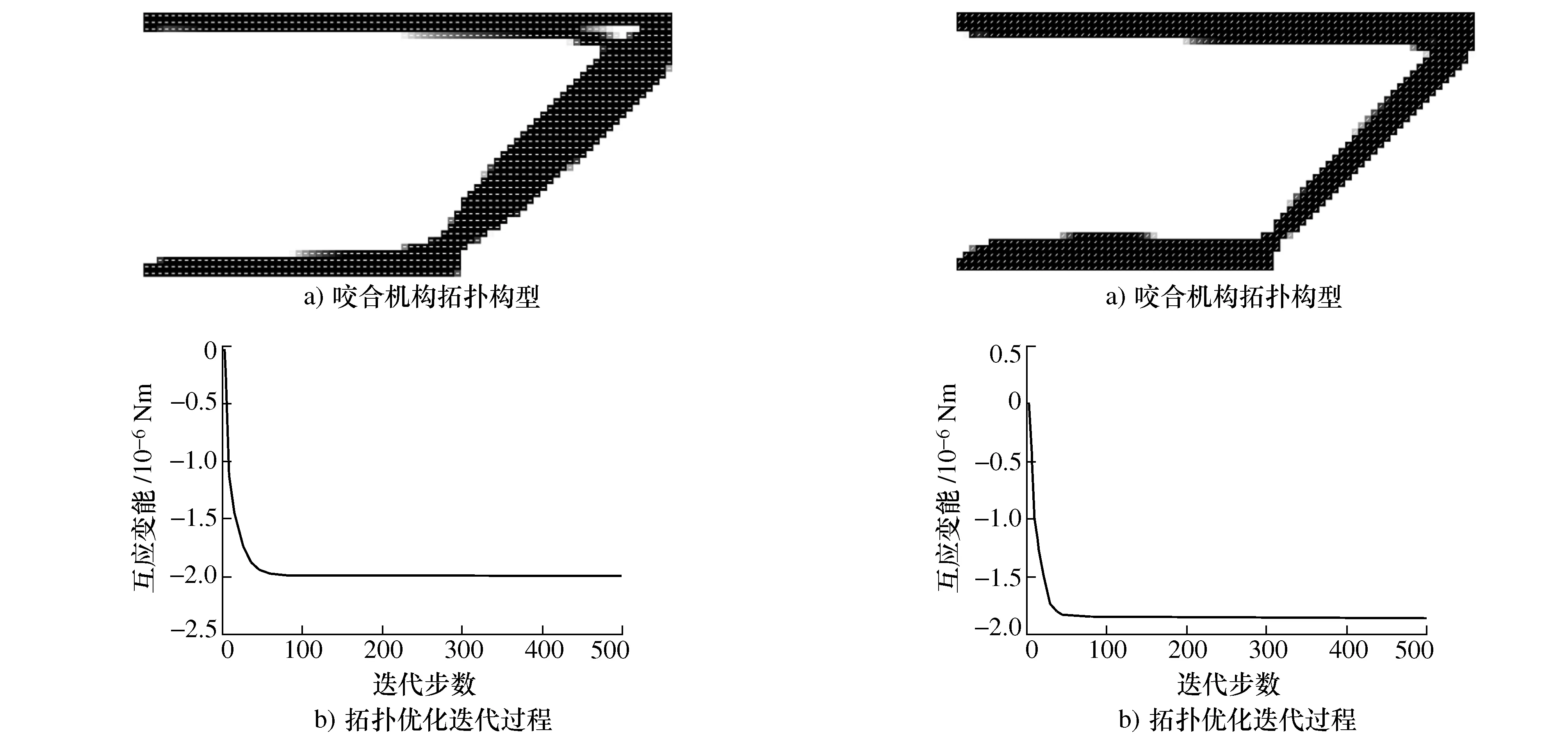
图8 纤维角度为0°的各向异性材料咬合机构拓扑优化 图9 纤维角度为45°的各向异性材料咬合机构拓扑优化

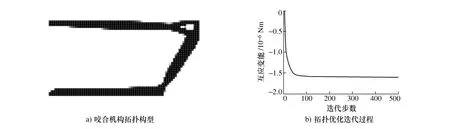
图10 纤维角度为90°的各向异性材料咬合机构拓扑优化

与纤维角度固定拓扑优化结果相比,考虑纤维角度变化拓扑优化获得的咬合机构构型有所不同,并且咬合机构的互应变能(2.354×10-6Nm)也更大,为纤维角度固定为0获得的咬合机构互应变能的1.18倍,考虑纤维角度变化进行咬合机构拓扑优化设计能够有效提高咬合机构的变形性能;同样,这表明提出的设计方法是有效的。

4 结论

本文提出了一种考虑纤维角度变化的各向异性材料柔顺机构拓扑优化设计方法,采用改进的固体各向异性材料惩罚模型引入变化的设计单元纤维角度,构建考虑纤维角度变化的各向异性材料柔顺机构拓扑优化数学模型,采用移动渐近算法(MMA)更新设计变量,通过数值算例验证提出设计方法的有效性。可以得出以下结论:

1) 考虑纤维角度变化拓扑优化获得的柔顺机构构型中纤维角度会进行相应的调整,以使得机构的互应变能达到最大。

2) 与固定纤维角度拓扑优化结果相比,考虑纤维角度变化拓扑优化获得的柔顺机构构型有所不同,并且机构的互应变能有较大提高,其中,夹持器的互应变能提高了45%,咬合机构的互应变能提高了18%。

3) 考虑纤维角度变化拓扑优化获得的柔顺机构的变形性能有显著提高,但是没有考虑到强度失效问题,如何将本文方法扩展到各向异性材料柔顺机构强度设计问题,将是今后的研究工作重点。