基于触点接触的导电滑环的接触力学分析

孙 斌，冯 静，沈 彤，申 振

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

滑环主要是用来传输电源和信号的机电装置，主要的零部件有接触电刷组件、导电环、刷架座、主轴等部件，通过接触电刷组件与导电环滑动接触来传递电流、信号等。目前广泛应用的汇流环接触结构形式主要有活塞式结构、簧片悬臂式结构、金属刷丝结构等。这3种结构的接触形式各有优缺点，其中悬臂式结构靠簧片产生接触压力，在簧片末端安装触点，触点磨损量较少，压力在很长时间内可以保持稳定，对于传输大电流，可采用簧片并联方式。本文以触点与导电环的接触形式进行接触应力分析。

吴加俊等以单丝电刷与导电环为接触对象，基于赫兹理论推导出了接触应力解析公式，并通过有限元软件 ABAQUS模拟仿真分析，将有限元分析与理论解进行对比，验证了解析公式的正确性。周文韬等对单丝电刷导电滑环进行了二维结构有限元仿真分析，并建立了导电滑环机械磨损寿命预测的理论公式。马春生等针对一种新型大功率滚动式汇流环装置，利用三维软件 Solidworks 进行参数化建模，然后导入有限元软件Ansys Workbench 后进行静力学分析，得到了内、外环上接触应力的分布情况。文广对以某滑动式汇流环的主要结构——金属丝-环芯摩擦副为研究对象，利用有限元法对其进行瞬态动力学分析，考察结构在冲击载荷作用下的瞬态响应，研究转速和冲击载荷大小对其瞬态响应的影响。

本文以触点与导电环为接触对象，将其抽象为球体与凹槽面的接触形式，给出基于赫兹接触应力的公式，并基于Matlab设计了接触应力的图形用户接口(GUI)界面，利用Ansys Workbench 对模型进行接触应力对比分析，验证了理论公式的正确性，为接触组件的耐磨特性做进一步的研究打下基础。

1 触点导电滑环的几何模型

导电滑环现实中的工作状态如图 1 所示，电刷通过与导电环接触产生弹性力，电刷作为风电滑环核心零件，由贵金属电刷触点、弹性刷臂组成。电刷末端焊有触点，靠弹性力触点与导电环保持稳定接触。

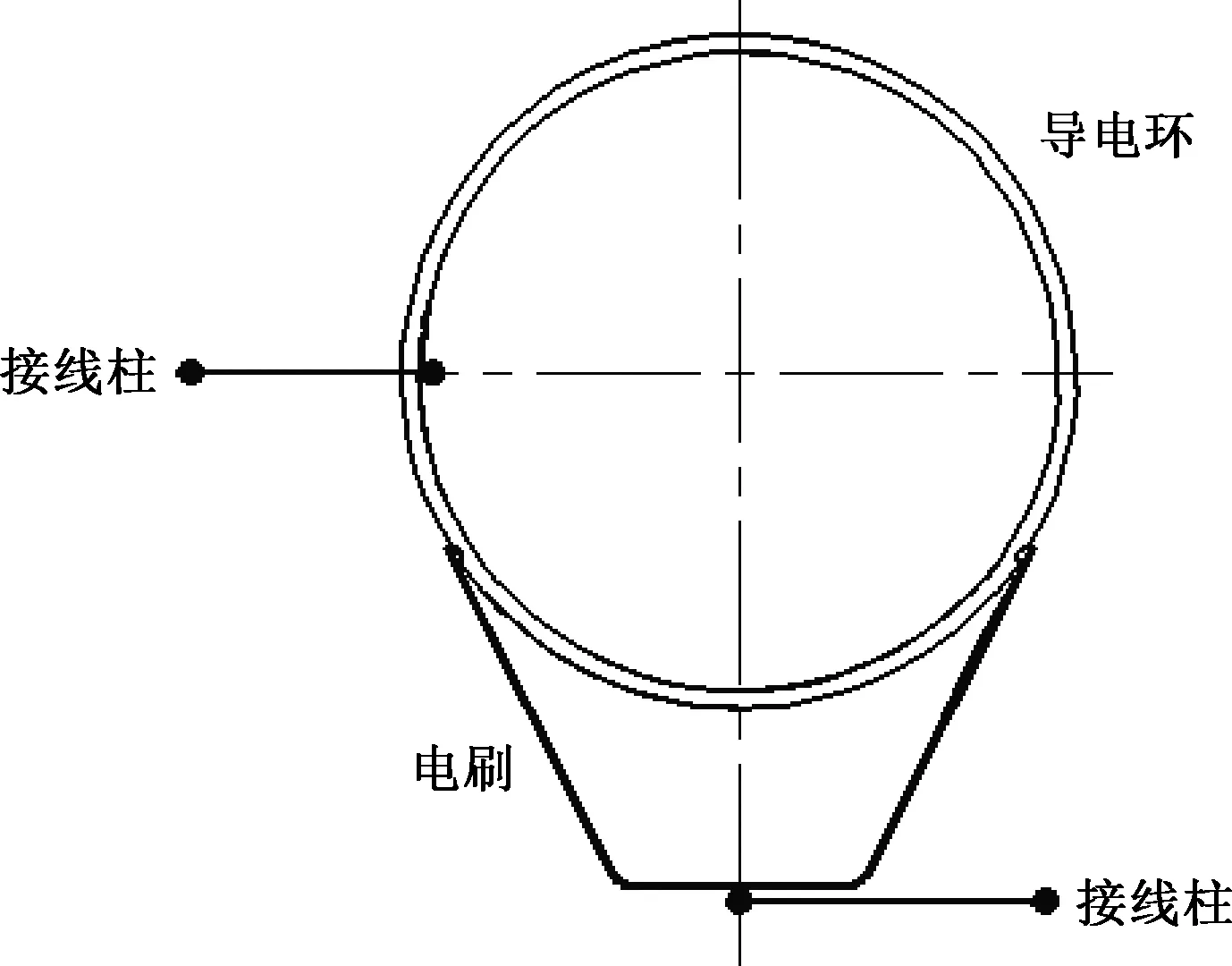
图1 触点导电滑环工作原理图

为了简化分析，取触点与导电环接触的那一部分进行分析，将导电环简化为圆弧凹槽结构，凹槽半径为，触点为光滑的半球体结构，半径为，凹槽圆柱体的半径为，两者在刚刚接触还未变形时，只有一个公共的点对点接触点，如图 2所示。由此，该几何模型就被抽象为圆弧凹槽面与半球体接触的状态。

图2 触点导电滑环接触模型

根据文献[7]提供的任意曲面的赫兹型点接触问题的求解，赫兹认为在接触区域，曲面上任意两点之间的距离为：

(1)

接触区域的接触应力分布与接触区域点的位置有关，在接触区域中心点的应力最大，边缘上的应力为零。一般假设接触应力呈半椭球状分布：

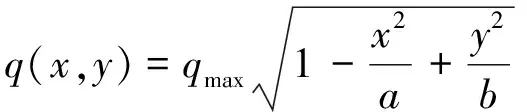
(2)

式中:表示接触区域的最大接触应力；，表示接触区域椭圆的长轴与短轴。

根据接触应力与外力平衡的关系：

(3)

式中:表示受到的外力。

这样求解接触应力就变成了求解、、在考虑接触变形过程中必须满足协调方程，利用波西呢斯克解，得到接触区域参数如下：

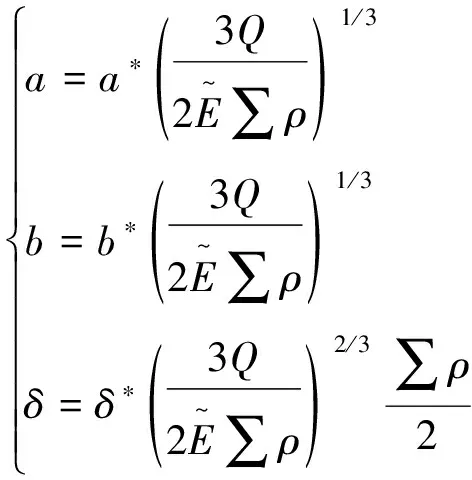
(4)

至此，最大接触应力就可以求得。近似计算方法参考文献[7]的第2种近似计算方法。

2 MATLAB的GUI界面设计

为了方便计算接触应力与接触变量，特设计了GUI界面，采用文献[7]第2种近似计算方法的GUI界面如图3所示。

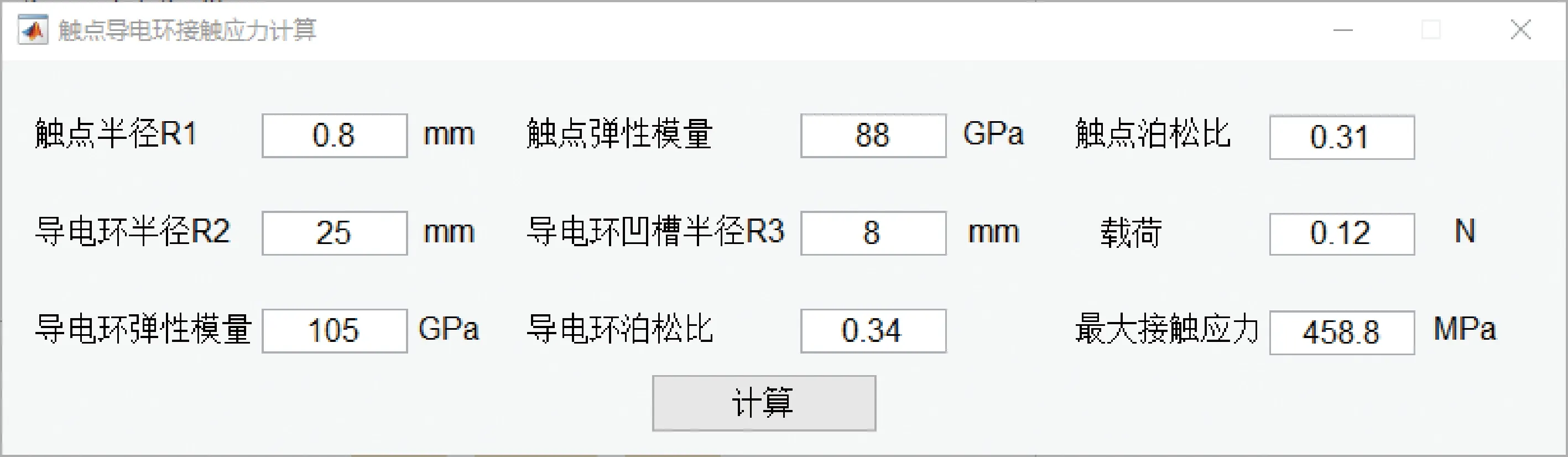
图3 触点接触应力GUI界面

3 有限元仿真分析

为了实现对触点电刷接触的有限元仿真分析，设计以下利用 Ansys Workbench14.5软件进行仿真的分析流程：

(1) 首先，在 Ansys Workbench14.5里建立触点与导电环的接触模型，触点的材料为 AgNi，密度=10 g/cm，弹性模量=88 GPa，泊松比=0.31，触点半径=0.8 mm，导电环材质为铜，半径=25 mm，凹槽半径=8 mm，弹性模量=105 GPa，泊松比=0.34。为了节省计算机资源，这里只取导电环与触点接触的部分分析，并利用四分之一模型进行分析。

(2)网格划分：网格划分采用Ansys Workbench14.5自动划分的方式，这样划分出来的网格并不能保证接触状态的计算精度。为了保证接触计算的精度，触点与导电环的接触区域采用 Sphere of Influence 的局部网格划分方式进行精细划分，共生成有限元单元150 399个，建立的网格有限元模型，如图 4 所示。对有限元模型施加载荷与约束，进行求解，求解的载荷0.12 N的接触应力图如图5所示。有限元解与理论解的对比结果如表1所示，有限元解与理论解误差相差不大。

表1 触点与导电环接触有限元解与理论解结果对比表

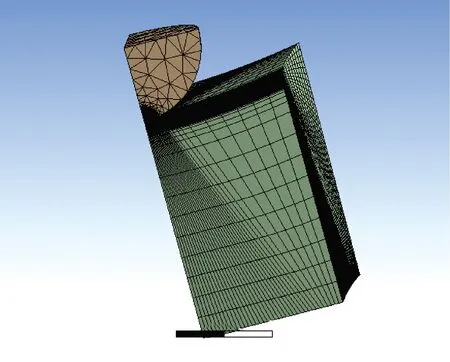
图4 触点接触有限元模型

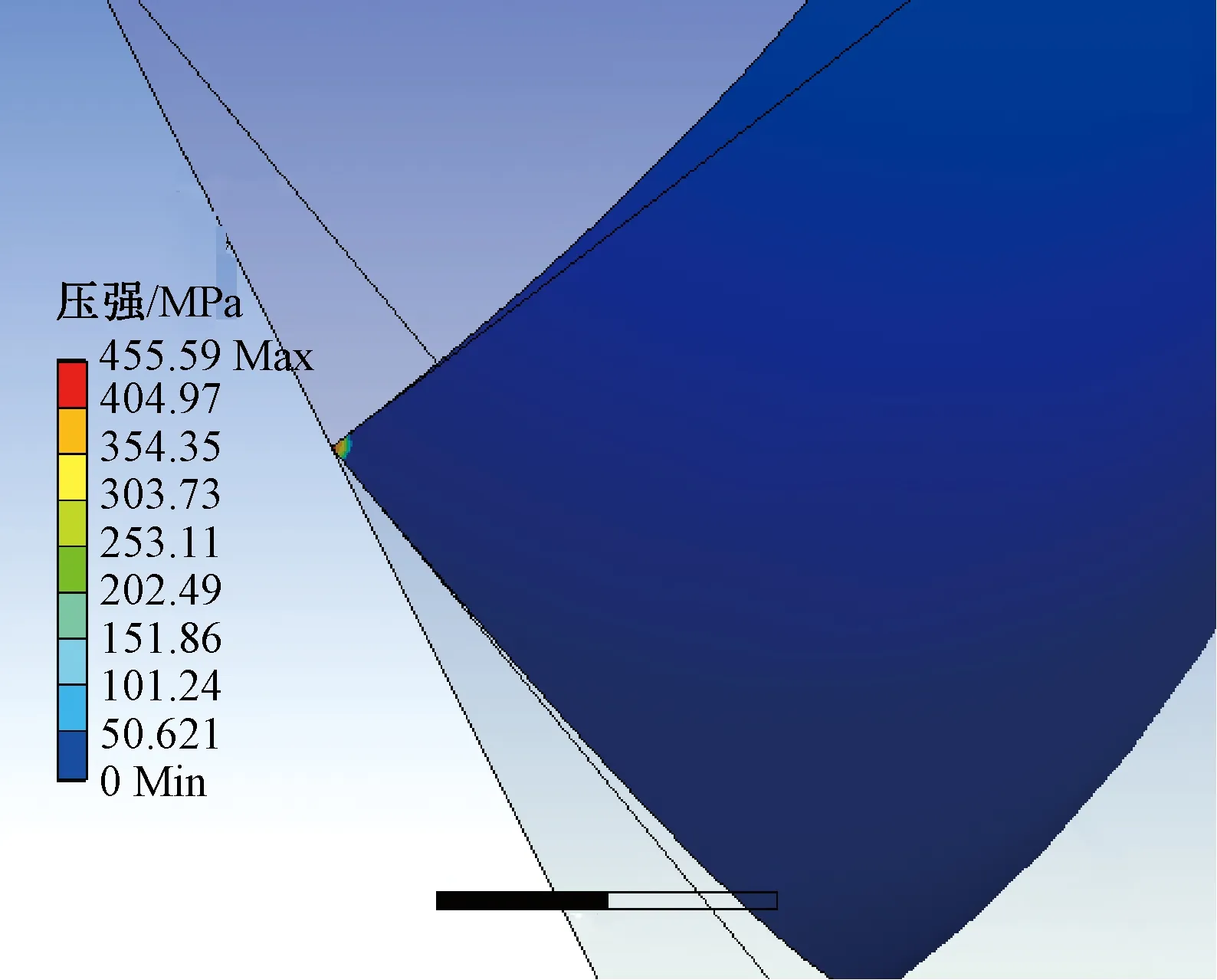
图5 载荷0.12 N下的有限元解

4 结 论

(1) 将触点和导电环的接触抽象为圆弧凹面与半球体接触的几何模型，结合深沟球轴承有关赫兹接触应力的公式，给出圆弧凹面与半球体接触的解析公式。

(2) 为了方便工程计算，编写了基于解析公式的MATLAB的GUI界面。

(3) 基于ANSYS WORKBENCH对接触模型进行了有限元分析，分析了不同载荷下的有限元解，将有限元解与理论解进行分析对比，2种解误差较小，验证了解析公式的有效性。