基于半正定松弛的赋形方向图主瓣波纹控制方法

窦修全，胡孟凯，杜宇峰，苗 峻

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北省电磁频谱认知与管控重点实验室，河北 石家庄 050081)

0 引 言

赋形方向图综合技术可以实现特定区域的照射，提高能量增益，因此该技术在雷达、声呐、卫星通信等领域具有广泛的应用前景。近年来，研究人员已经提出了很多赋形方向图综合方法。这些方法大致可以分为以下几类。一类是基于梯度的优化方法，李欣等提出了一种基于Broyden-Fletcher-Goldfarb-Shanno (BFGS)的赋形方向图综合方法，J.Liang等提出了2种基于交替方向乘子法(ADMM)的方法，但这类方法需要多次迭代，且容易陷入局部最优解。另一类是基于进化算法的优化方法，D.W.Boeringer等提出了一种基于粒子群优化(PSO)的方法，Y.Jiang等提出了一种基于遗传算法(GA)的优化方法，这类方法可以找到全局最优解，但需要调整大量参数。另外，还有一类基于凸松弛的方法，这类方法是目前应用最多的，B.Fuchs等提出了一种基于序贯凸优化(Sequential convex optimization)的方法，B.Fuchs提出了一种基于半正定松弛(SDR)的方法，P.Cao等提出了一种基于二阶锥规划(SOCP)的方法，Q.Lu等提出了一种基于一阶迭代凸近似的方法。这类方法通过约束主瓣和旁瓣的幅度寻找可行解，从而使得到的方向图逼近期望的赋形方向图，但当给定的主瓣约束不合适时，往往找不到可行解。针对这一问题，本文提出了一种基于半正定松弛的主瓣波纹控制方法，该方法将主瓣波纹控制表示为一个最优化问题，然后通过半正定松弛技术得到该问题的解。仿真结果表明，该方法更加稳定，使赋形方向图综合问题总能找到可行解，且能有效地降低赋形方向图的主瓣波纹。

1 问题建模

假设有一均匀线阵，如图1所示，阵元数为，阵元间距为，则该阵列的阵因子为：

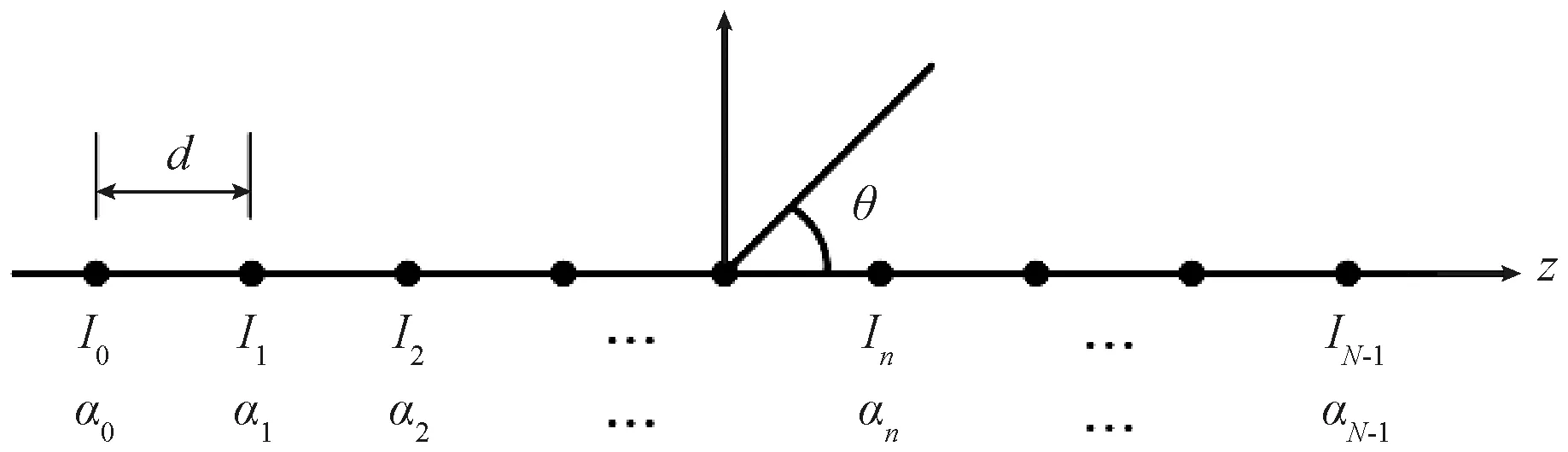
图1 均匀线阵模型

(1)

式中：和分别为各阵元激励的幅度和相位；=2π，为波数，为波长。

令：

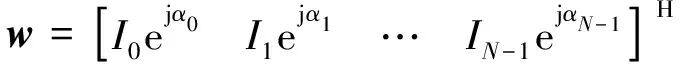
(2)

(3)

则式(1)可改写为矢量形式：

()=()

(4)

式中：为激励矢量；()为导向矢量。

已有的方法通过约束主瓣和旁瓣的包络来寻找可行解，可用如下模型表示：

式中：表示主瓣区域；()和()分别表示主瓣的下界和上界，上界与下界的差值表示主瓣的波纹；表示副瓣区域；()表示副瓣的上界。

但是当给定的主瓣约束不合适时，比如式(5b)中的上界与下界太接近时，该方法可能找不到可行解，但如果上界与下界相距较远时，主瓣波纹又会过大。针对这一问题，本文提出了基于半正定松弛的主瓣波纹控制方法。该方法将主瓣波纹控制表示为一个最优化问题，既能保证总能找到可行解，又能尽可能降低主瓣波纹。根据这一思想，可将式(5)改写为：

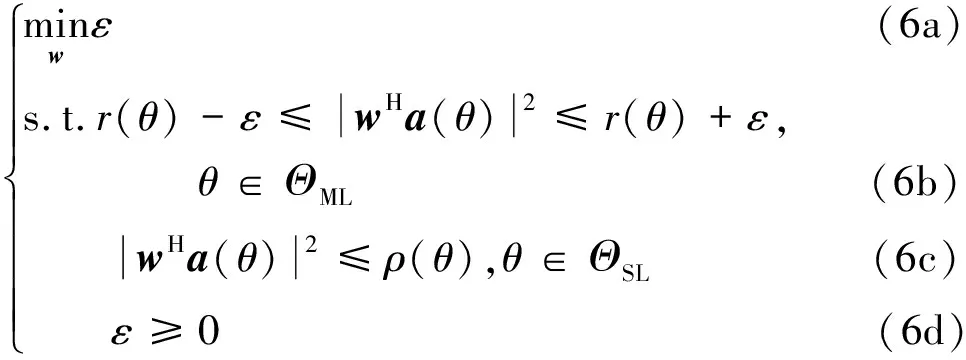
式中：()表示期望的主瓣形状；2表示主瓣波纹的大小。

式(6)的含义是在获得期望的赋形方向图的同时，最小化主瓣波纹。

2 优化求解

式(6b)包含非凸约束，所以式(6)为一个非凸问题，很难直接优化求解，因此本文采用半正定松弛技术来求解。

首先对式(6)进行等价变换，令=，=()()，则式(6)等价于：

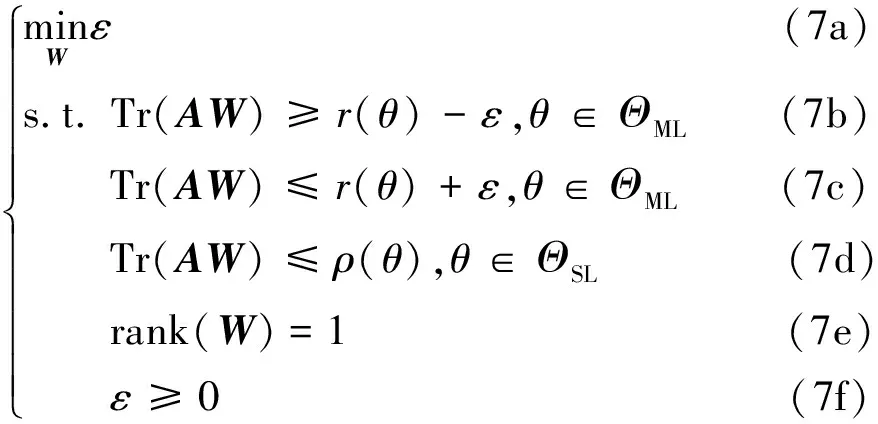
式中:仅有式(7e)为非凸约束，忽略该约束，可得到一个标准的凸问题，该问题可通过CVX求解。

在得到最优解后，为了满足式(7e)，还需要从中抽取秩1向量，常用的方法为特征值分解，即最优的激励向量为:

(8)

式中：为的最大特征值;为其对应的特征向量。

3 仿真实验

为了验证该方法的有效性，本文进行了一组仿真实验，对比了本文方法和文献[10]中方法实现的不同参数的平顶方向图的主瓣波纹大小。仿真参数设置为：阵元数=20，阵元间距=2。所有实验都在64位PC机上完成，CPU为Intel Core (TM) i5-7500 CPU，随机存储器(RAM)为4 GB，使用的仿真软件为64位的MATLAB R2012b。

图2～图4对比了波束中心相同、波束宽度不同的平顶方向图，图3与图5对比了波束中心不同、波束宽度相同的平顶方向图。可以发现，本文提出的方法均能获得比参考方法更小的主瓣波纹，尽管仅提高了约0.1 dB，但将主瓣波纹控制表示为一个最优化问题，避免了人工设置参数不合适时可能找不到可行解的问题，因此，该方法更加稳定。

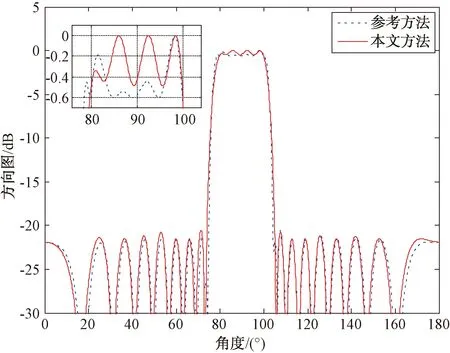
图2 波束中心为90°，波束宽度为20°的平顶方向图对比

图3 波束中心为90°，波束宽度为30°的平顶方向图对比

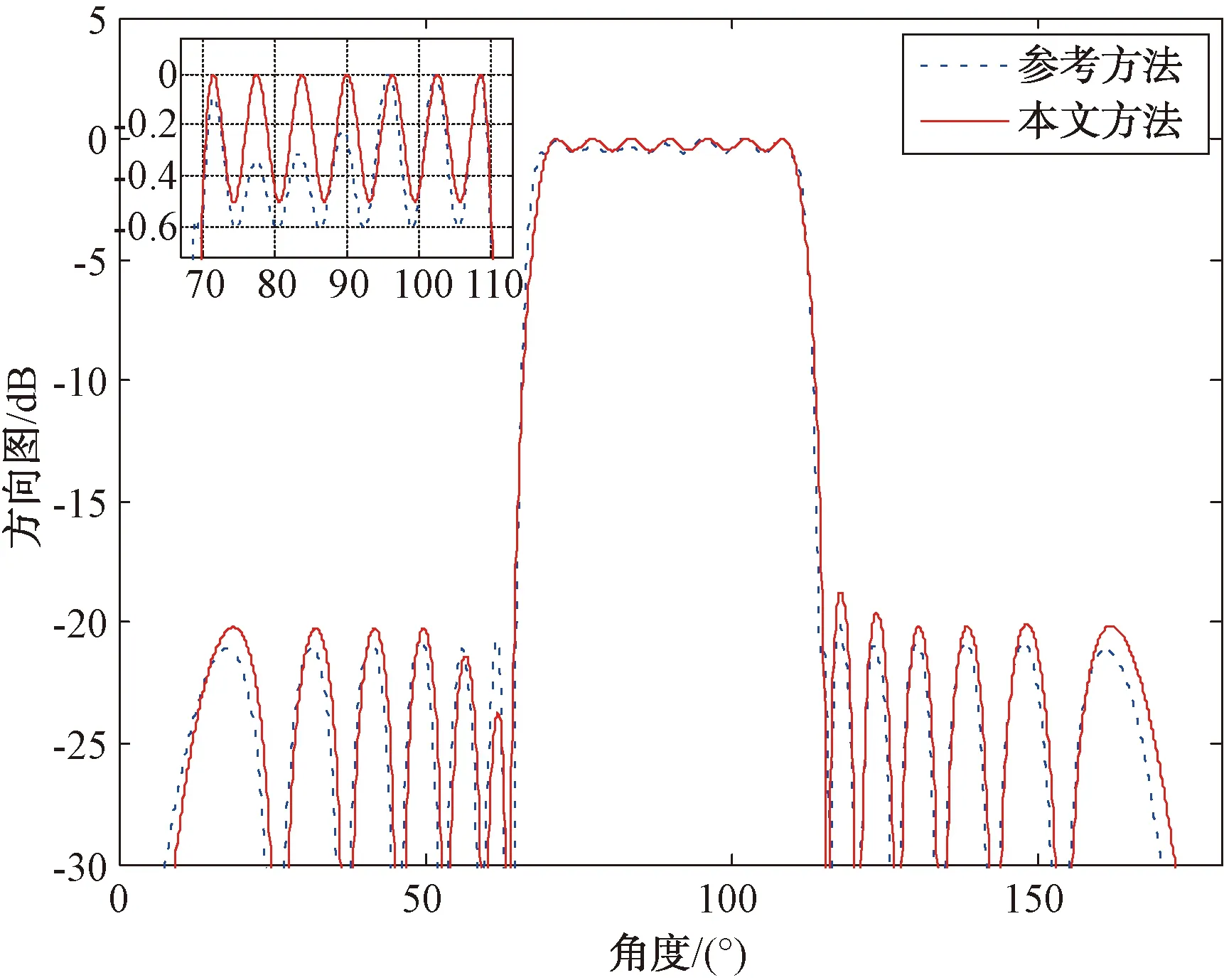
图4 波束中心为90°，波束宽度为40°的平顶方向图对比

图5 波束中心为60°，波束宽度为30°的平顶方向图对比

4 结束语

已有的赋形方向图综合方法在给定的主瓣约束不合适时，可能找不到可行解，因此不能有效地控制主瓣波纹。针对这一问题，本文提出了一种基于半正定松弛的主瓣波纹控制方法，该方法将主瓣波纹控制表示为一个最优化问题，然后通过半正定松弛技术得到该问题的解。仿真结果表明，该方法更加稳定，使赋形方向图综合问题总能找到可行解，且能有效地降低赋形方向图的主瓣波纹。