地铁曲线波磨段e型弹条大圆弧共振断裂因素研究
吴浩,韦凯,王显,李昕,王平
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都610031;2. 西南交通大学 土木工程学院,四川 成都 610031)
弹条作为扣件系统中的关键部件,为轨道结构提供必要的扣压力。近年来,地铁线路中弹条失效现象时有发生,严重危及行车安全。基于e型弹条的断裂原因分析已有较多研究。在弹条受力状态分析方面,陈宪麦等[1-2]应用有限元方法计算分析了e型弹条在服役条件下的应力状态,认为小圆弧处应力集中是造成弹条小圆弧处断裂的原因。尚红霞等[3]通过研究弹条安装状态下的受载特征规律,发现弹条中肢插入铁垫板孔过深导致弹条小圆弧与中肢连接处产生应力集中,使得弹条在列车荷载作用下于小圆弧处发生断裂。张松琦等[4]针对e型弹条过安装导致的小圆弧断裂问题,提出了e 型弹条结构优化方案。在弹条动力特性研究方面,尚红霞[5]应用模态分析方法得到e 型弹条自由状态下的固有频率及其振型特征。进一步地,THOMPSON 等[6]通过试验研究发现,不同服役状态下弹程(扣压力)会对弹条高频振动特性产生影响,弹条固有频率与其安装弹程密切相关。在此基础上,王绍华等[7]提出一种基于模态分析的弹条扣压力测试方法,通过测试安装状态下扣件弹条固有频率,即可间接得到弹条的实际扣压力。为了科学探究钢轨波磨对弹条的激振影响,肖宏等[8]应用时频域响应关系分析方法,分析研究了弹条固有振动特性。研究发现,弹条固有频率与波磨通过频率一致引发共振,导致小圆弧处拉压、扭转应力增大,引起该位置断裂。以往研究表明,钢轨波磨引起弹条共振是导致弹条异常断裂的主要外因,另外,弹条安装过程中小圆弧处容易产生应力集中也造成不利影响。这些研究均是集中在分析弹条小圆弧断裂的影响因素,鲜有研究能够探究弹条发生大圆弧断裂的原因。鉴于此,本文应用非线性有限元法和模态分析方法,结合运营线路现场波磨测试结果,深入研究曲线段钢轨波磨对e 型弹条的激振影响,分析e 型弹条断裂失效的影响因素,以期解释弹条大圆弧处折断原因。
1 现场调研
某地铁快线设计时速120 km/h,运营线路地处沿海区域,气候湿热,轨道结构服役环境较为潮湿。该线大量铺设了DTⅢ型扣件系统,自开通运营后,线路曲线段陆续出现扣件弹条断裂失效现象,并伴随出现钢轨波磨病害。根据现场弹条断裂统计调研情况可知,e 型弹条断裂位置主要集中在弹条小圆弧和大圆弧两处,如图1所示。

图1 现场弹条断裂情况Fig.1 Fracture condition of clip on site
现场通过钢轨波磨测试装置CAT 对波磨较为严重的曲线段进行了测试。测试结果发现,钢轨波磨主要出现在小半径曲线段(R800 和R700),钢轨波磨波长范围为20~50 mm。其中,主要波长表现为31~40 mm,列车以103 km/h 速度通过时,对应波长31~40 mm 波磨导致的通过频率为715~923 Hz。
2 e型弹条三维非线性有限元模型
2.1 有限元模型
本文基于DTⅢ型扣件系统建立弹条有限元模型。模型主要包括弹条、轨距挡块以及铁垫板局部。单元类型选用四面体实体单元,模型共划分73 997个网格和15 343个节点,如图2所示。

图2 有限元模型Fig.2 Finite element model
2.2 材料属性
e 型弹条材料采用60Si2MnA,其本构模型采用理想双线性强化弹塑性模型,弹条屈服强度为1 375 MPa,极限强度为1 570 MPa。轨距挡块材料为玻璃纤维增强聚酰胺66,铁垫板材料采用QT450-10球墨铸铁,材料详细参数见表1。
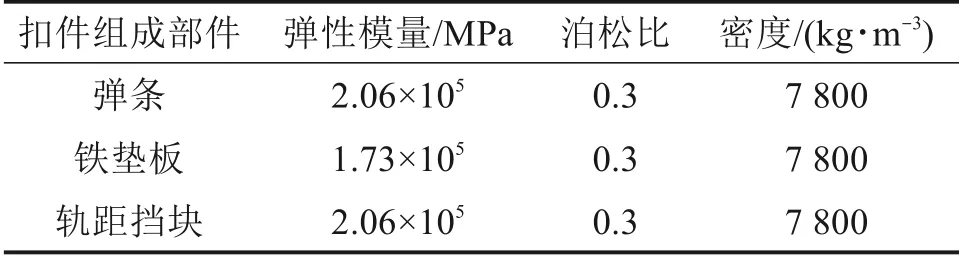
表1 材料参数Table 1 Material parameters
2.3 接触关系设置
e 型弹条正常服役状态下边界条件复杂,采用非线性接触理论处理弹条与铁垫板之间的接触状态[9-10],接触算法采用增广拉格朗日算法。模型部件各部分接触关系设置见表2。

表2 接触关系设置Table 2 Contact settings
3 弹条刚度非线性模态分析理论
弹条的固有模态频率与其自身刚度有关,为反映弹条在真实受载条件下的固有频率,需要充分考虑引起弹条刚度变化的影响因素。因此,本文结合弹条刚度非线性特性和模态分析方法,研究弹条刚度特性对其固有频率的影响规律。
3.1 模态分析
模态分析是常用于研究结构振动特性的一种方法。根据弹性力学建立弹条系统运动方程:

式中:[M]为弹条的质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{x}为弹条位移向量,其1 阶导数{x}为弹条振动速度向量;{F(t)}为弹条所受的外界荷载向量。当F(t)=0 时,得到扣件系统自由振动方程。在弹条的动力特性分析过程中,通常不考虑阻尼的作用及影响,即可得到无阻尼振动方程为:

得到相应的特征方程为:

式中:方程的根ωi为弹条第i阶模态固有频率(i=1,2,…,n)。
3.2 弹条刚度非线性
弹条的实际振动情况复杂,其固有振动特性与弹条趾端边界条件密切相关。在e型弹条的振动特性研究中,弹条趾端边界条件可以视作弹性边界支撑,从而可以通过边界弹簧来假定[11],如图3所示。因此,弹条趾端边界刚度可以等效为切向边界弹簧和法向边界弹簧的刚度。

图3 弹条趾端弹性约束边界条件Fig.3 Elastic constrained boundary conditions at the toe of clip
改变弹条边界约束条件,本质上是改变相关自由度上的边界刚度。在有限元计算中,对安装状态下的弹条进行实体单元划分处理,弹条单元刚度矩阵由2部分组成[12-13],如式(4)所示:
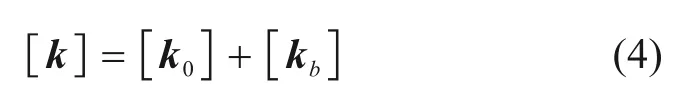
式中:[k0]为弹条自身固有刚度矩阵;[kb]为由边界约束条件所引起的附加刚度矩阵。
4 e型弹条静动力计算分析
4.1 弹条静力计算分析
应用有限元软件对e 型弹条安装过程进行静力计算分析,弹条中肢插入深度为68 mm,安装弹程13 mm。在弹条正常服役条件下,弹条小圆弧内侧区域和大圆弧内侧靠近铁垫板区域处应力较大,最大等效应力为1 487 MPa,小于弹条极限破坏强度,如图4所示。
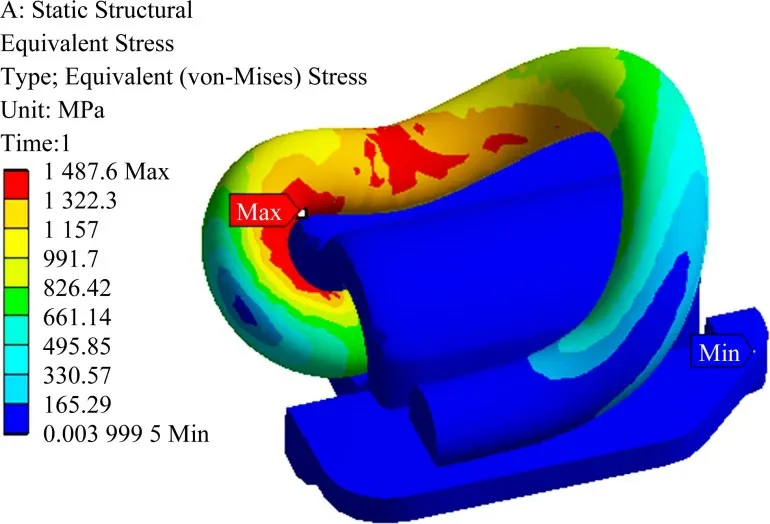
图4 等效应力Fig.4 Equivalent stress
弹条扣压力与弹程基本成线性关系,斜率约为1 kN/mm,如图5 所示。当弹条趾端变形达到初始弹程13 mm 时,由有限元模型计算得到的弹条安装状态下的扣压力为11.8 kN,满足扣件设计扣压力要求。

图5 扣压力与弹程的关系Fig.5 Relationship between the clip clamping force and clip displacement
4.2 弹条安装状态模态分析
弹条在正常安装条件下已经产生了趾端变形,此时弹条处于预应力状态,进一步计算得到弹条服役状态下的固有频率及其振动特性,见图6,对应振型描述与计算结果验证见表3。

表3 振型描述Table 3 Modal description

图6 安装状态弹条固有频率Fig.6 Natural frequency of clip in installation state
4.3 弹条共振条件下应力状态分析
图7是弹条在共振状态下的等效应力云图。弹条在第1 阶固有频率发生共振时,最大mises 等效应力点为弹条小圆弧与中肢连接处。弹条在第2阶固有频率发生共振时,最大mises 等效应力点为弹条大圆弧靠近跟端处。

图7 弹条共振条件下等效应力Fig.7 Equivalent stress of clip under resonance condition
扣件弹条实际受载情况是复合型受载模式,而在弯曲、拉压和扭转问题中,扭转问题的疲劳极限往往小于弯曲和拉压问题的疲劳极限。因此,弹条在共振状态下的剪应力最大处可能为弹条疲劳裂纹萌生的危险点,计算得到弹条在第1 和2 阶固有频率发生共振时的剪应力结果如图8所示。

图8 弹条共振条件下剪应力Fig.8 Shear stress of clip under resonance condition
本节计算得到的弹条等效应力与剪应力最大值与现场弹条小圆弧和大圆弧断裂位置高度吻合,这表明弹条在钢轨波磨的高频激励下引发共振是导致弹条断裂失效的重要原因。
5 曲线段e型弹条固有频率分析
轨距挡块是用来传递横向力、保持和调整轨距的重要部件,列车通过曲线段时,轨距挡块在较大的横向作用力下可能发生横向错动。由于弹条趾端直接扣压在轨距挡块上,因此弹条趾端边界条件与其接触面摩擦因数以及轨距挡块的位移错动密切相关。因此,轨距挡块在横向力作用下的稳定性会显著影响弹条的固有振动特征。
DTⅠⅠⅠ型扣件系统轨距挡块预留装配缝隙为1 mm,如图9 所示。铁垫板底脚距为169 mm(+1,-0.5),钢轨内侧轨距挡块厚度为8 mm,外侧轨距挡块厚度为10 mm,钢轨轨底宽150 mm。考虑到扣件安装时较大的装配误差和磨损状态等不利因素,取轨距挡块与铁垫板之间缝隙为1 mm。
轨距挡块横向受力可以分为2种情况,横向位移方向已在图9中标出。一种为轨距挡块在钢轨横向压力作用下向内横向错动;另一种情况是轨距挡块在钢轨的摩擦作用下向外横向错动。
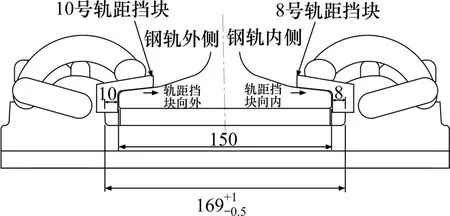
图9 DTⅢ扣件系统Fig.9 DT Ⅲfastener system
为了模拟列车过曲线段时扣件弹条的真实受载条件,本文在仿真计算中设置轨距挡块横向位移荷载范围为-1~1 mm,位移荷载工况间隔0.1 mm。
5.1 轨距块微动横移对弹条固有频率影响分析
轨距挡块横向移动可能会引起弹条趾端与轨距挡块接触面接触状态的变化,进而影响弹条趾端的约束边界条件,改变弹条的固有振动特性。
为了清晰地描述轨距挡块横向错动对弹条固有频率的影响规律,本节取接触面摩擦因数为0.5,在弹条趾端摩阻力条件一定的情况下,计算分析轨距块横移对弹条固有频率的影响,深入研究由边界条件变化引起的弹条非线性刚度特性对弹条固有振动频率的影响规律。
5.1.1 轨距块向内侧横移对弹条固有频率影响
以弹条正常安装状态为初始状态,当轨距挡块发生横移时,弹条趾端与轨距挡块发生相对滑动,趾端摩擦接触状态由黏着接触转变为滑动接触,并且随着轨距挡块继续横移,弹条趾端滑动接触面积逐渐增大并趋于稳定,如图10所示。

图10 趾端摩擦状态变化规律Fig.10 Variation of toe friction state
摩擦状态的改变会导致弹条趾端摩擦约束条件产生变化,为了能更加直观地描述弹条趾端摩擦约束条件随轨距挡块横移的变化规律,本文计算得到弹条趾端表面横向力位移曲线,将曲线斜率等效为弹条趾端受到的摩擦约束强度,如图11所示。通过该力位移曲线可以看出,随着轨距挡块从初始安装状态向内横移,弹条趾端摩擦约束能力首先大幅下降,然后随着轨距块向内横移,趾端摩擦约束能力逐渐上升并趋于稳定。

图11 弹条趾端横向力位移曲线Fig.11 Lateral force displacement curve of clip toe
弹条趾端与轨距挡块的切向摩擦约束主要影响弹条横向约束条件,而弹条第2阶模态振型为大圆弧横向摆动,因此轨距挡块向内横移将会显著影响弹条第2 阶固有频率,计算得到弹条第2 阶固有频率随轨距挡块向内横移距离的变化规律,如图12所示。

图12 第2阶固有频率与摩擦因数关系曲线Fig.12 Second order natural frequency and friction coefficient curve
由图11~12 计算结果可知,弹条第2 阶固有频率与弹条趾端摩擦约束能力密切相关。当轨距挡块向内侧横移时,弹条第2 阶固有频率降低186 Hz。随着弹条趾端约束边界条件先大幅减弱再缓慢增强的趋势,弹条第2阶固有频率也随之呈现出先大幅降低再小幅度上升并逐渐趋于稳定的变化规律。
5.1.2 轨距块向外侧横移对弹条固有频率影响
当轨距挡块从安装位置向外侧横移时,弹条趾端与轨距挡块始终保持黏着接触状态,弹条趾端在较大的摩擦力作用下跟随轨距挡块移动,相对滑移量较小。当横移距离较大时,弹条趾端与轨距挡块黏着接触区域出现小幅度缩小的趋势,如图13所示。
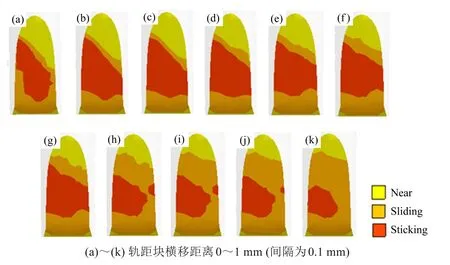
图13 趾端摩擦状态变化规律Fig.13 Variation of toe friction state
图14 是轨距挡块向外侧横移时弹条趾端表面力-位移关系曲线图。由于弹条趾端与轨距挡块摩擦接触状态较为稳定,当轨距挡块从安装初始状态向外出现微小横移时,曲线斜率基本成线性关系,但随着轨距挡块向外横向位移增大,曲线斜率出现逐渐减小的趋势,这表明弹条趾端摩擦约束强度将会随着横移距离增大而小幅度减弱。

图14 弹条趾端横向力位移曲线Fig.14 Lateral force displacement curves of clip toe
由图15~16 计算结果可知,轨距挡块向外侧横移对弹条第2阶固有频率的影响有限。随着轨距挡块向外侧横移距离的增大,弹条趾端摩擦约束条件逐渐减弱,会导致第2 阶固有频率小幅度减小,当横移距离为1 mm时,频率减小约68 Hz。
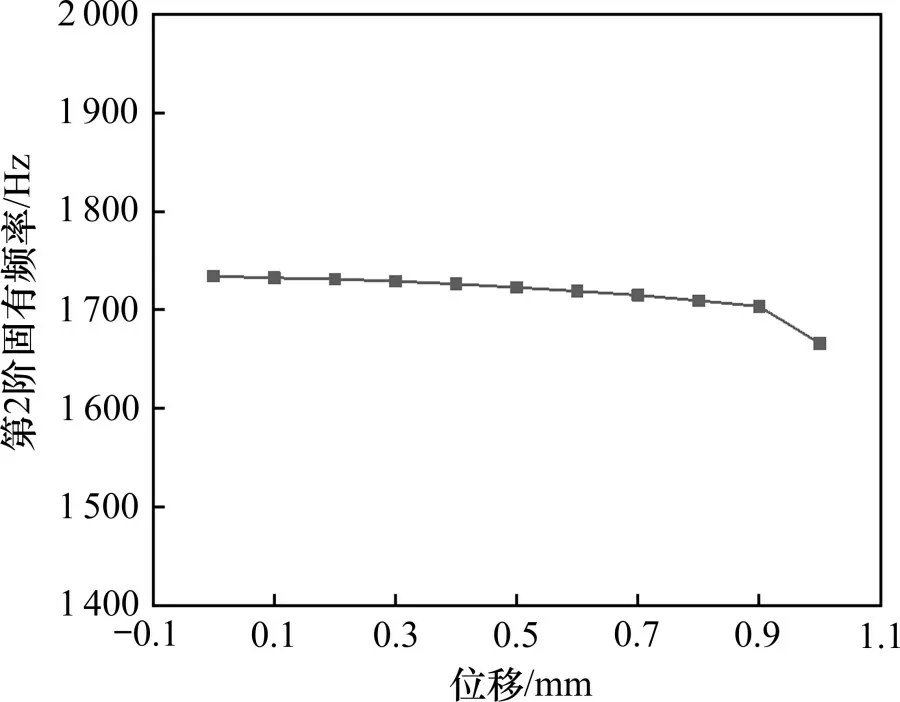
图15 第2阶固有频率与摩擦因数关系曲线Fig.15 Second order natural frequency and friction coefficient curve
5.2 弹条趾端不同摩阻力条件下轨距块微动对弹条固有频率影响分析
弹条趾端摩阻力受线路运营环境条件影响明显。在湿热多雨的沿海地区,线路地下区间隧道内外温差大,隧道内部湿度大[14],而线路高架区间则直接暴露于湿热环境中,总之,湿热地区地铁整体运营环境较为潮湿,长期的潮湿环境将会减小弹条趾端与轨距挡块接触面之间的摩阻力。
考虑到弹条趾端与轨距挡块之间的摩阻力对接触状态的影响,本节取弹条趾端与轨距挡块之间摩擦因数变化范围为0.1~0.5[15-16],计算分析不同摩擦因数条件下,轨距挡块微动对弹条固有频率的影响规律。
5.2.1 弹条趾端不同摩阻力条件下轨距挡块向内侧横移对弹条固有频率影响
当轨距块向内侧横移时,不同摩擦因数条件下弹条趾端力位移关系曲线如图16 所示。由图中曲线斜率的变化规律可知,当轨距挡块向内侧横移时,弹条趾端的摩擦接触状态在不同摩擦因数条件下均会从黏着接触突变为滑动接触。随着弹条趾端与轨距挡块接触面摩擦因数的减小,趾端摩擦状态越易发生突变。

图16 弹条趾端横向力位移曲线Fig.16 Lateral force displacement curves of clip toe
由图17 计算结果可知,弹条趾端摩阻力的降低会导致弹条第2阶固有频率显著降低,当轨距挡块横向位移为0 mm,摩擦因数从0.5 降低为0.1时,固有频率降低幅值约为266 Hz。随着轨距挡块横向位移由0 mm 变化为1 mm(向内横移),不同摩擦因数条件下弹条第2 阶固有频率均会显著降低,且摩擦因数越小,减小幅度越大,当弹条趾端与轨距挡块的摩擦因数为0.1 时,减小幅值可达380 Hz,此时,弹条第2 阶固有频率将会骤减到约1 088 Hz,接近现场波磨较为严重区段的波磨通过频率,进而引发弹条共振。

图17 第2阶固有频率与摩擦因数关系曲线Fig.17 Second order natural frequency and friction coefficient curves
5.2.2 弹条趾端不同摩阻力条件下轨距块向外侧横移对弹条固有频率影响
当轨距块向外侧横移时,计算得到的弹条趾端横向力位移关系如图18 所示。不同摩擦因数条件下,弹条趾端摩擦约束强度均会随着轨距挡块的向外横移呈现逐渐降低的趋势,且摩擦因数越小,该趋势越明显。其中,由图18 可以看出,当弹条趾端摩擦力较小时(摩擦因数为0.1),趾端与轨距挡块发生相对错动,导致弹条趾端摩擦约束作用显著降低。

图18 弹条趾端横向力位移曲线Fig.18 Lateral force displacement curves of clip toe
相比于轨距挡块向内横移的情况,轨距挡块向外横移对弹条趾端摩擦约束条件的影响较小,因此弹条第2阶固有频率减小幅值也相对较小,如图20 所示。但随着弹条趾端与轨距挡块之间摩擦因数的降低,当横移距离较大时,弹条第2阶固有频率同样会显著降低。若弹条趾端与轨距挡块的摩阻力过小,还会引起趾端与轨距挡块的相对错动,导致弹条第2阶固有频率骤降,甚至接近现场波磨通过频率。

图19 第2阶固有频率与摩擦因数关系曲线Fig.19 Second order natural frequency and friction coefficient curves
6 结论与建议
1)e 型弹条在第1 阶固有频率发生共振时,弹条最大等效应力与剪应力位置出现在小圆弧与中肢连接处;e型弹条在第2阶固有频率发生共振时,弹条最大等效应力与剪应力位置出现在大圆弧靠近跟端位置处。该计算结果得到的应力状态危险位置与现场断裂位置高度吻合。
2) 地铁列车通过小半径曲线段时,轨距挡块会在横向作用力下产生微动,导致弹条趾端边界条件改变,进而影响弹条第2阶固有频率,尤其是当轨距挡块向弹条跟端方向错动时,弹条第2阶固有频率大幅下降。
3) 弹条趾端与轨距挡块之间的摩擦因数是影响趾端边界条件的重要因素。弹条趾端摩阻力过小会导致弹条趾端约束能力显著降低,摩擦因数越小,弹条第2阶固有频率越低,并且在轨距挡块产生错动时,弹条第2 阶固有频率降低幅度增大,接近钢轨波磨通过频率,从而引发弹条在第2阶固有频率发生共振,造成弹条大圆弧断裂失效问题。

