基于离散元模型的水泥注浆岩样渗透率演化研究

周栋，丁文其，陈晓庆，张清照，罗泽军

(1. 同济大学土木工程学院地下建筑与工程系，上海，200092；2. 同济大学岩土及地下工程教育部重点实验室，上海，200092)

注浆技术已被广泛应用于地下工程、石油工程、水利坝体工程等工程实践。对裂隙岩体进行注浆不仅能提高岩体的力学性能，而且能显著改变其渗透特性，但目前注浆理论的发展还远远落后于工程实践。在岩体工程的建设与使用过程中，施工扰动及运行中的不确定荷载均会对岩体的力学性能、裂纹的萌生与扩展造成不同程度的影响，且随着裂隙扩展，岩体内部极易形成渗水通道而引发涌水问题，严重时将造成突水灾害。为更好、更安全、更经济地进行工程建设，需要进一步分析不同应力状态下岩体渗透性能的演化规律，揭示其内在机理。

目前，学者们对完整岩石在不同工况下的渗透性能进行了研究。BRACE 等[1]研究了Westerly花岗岩在高围压与高孔压下的渗透性变化规律，认为花岗岩的渗透性受围压与孔压的共同控制，随着有效围压增大，岩样的渗透率降低；LI 等[2]对砂岩全应力-应变曲线渗透性进行了研究，通过砂岩全应力-应变曲线试验得到应力与渗透系数之间的关系。研究表明砂岩的有效应力与渗透系数之间存在3种常见的函数关系即指数、乘幂和多项式关系[3-4]；韩国锋等[5]总结了大量岩石全应力-应变过程中的渗透性试验结果，发现在围压为1～40 MPa，97%的岩样峰值应力时其渗透率与初始渗透率的比值不会超过1 000 倍。采用充填材料后，裂隙岩体的渗透性受到很大影响；陈金刚等[6]以花岗岩为裂隙壁，进行了脆-塑性充填材料的渗透性试验；赵恺等[7]发现无论在加载还是卸载阶段，不同围压下双倍隙宽充填裂隙的渗透率均最低；王鹏飞等[8]采用3D 打印技术研究了10 级粗糙度的贯通充填裂隙类岩石试件的渗透特性，发现围压对贯通充填裂隙渗透率的影响处于主导地位；ZHOU等[9]对不同充填厚度的花岗岩标准试样进行了试验研究，发现充填试样的渗透率在峰值应力附近会大幅度提高。

试验研究表明，注浆虽然能降低岩体的渗透率，但不同的加载应力作用能够引起注浆岩体内部的裂纹萌生和扩展，使得注浆岩体的渗透率发生改变，当裂纹贯通时，岩体的渗透率将大幅度提高。但是既有三轴试验仪器不能实现对岩样裂纹发展的直接观测，为克服室内试验的不足，数值模拟方法逐渐被广泛采用。杨天鸿[10]运用数值软件模拟了岩样在孔隙水压作用下的加载破坏过程；ZHANG等[11]将岩体当成连续介质，考虑到岩体介质的非连续性与大变形特性，采用有限差分法分析了岩体的渗透演化过程；离散元方法已经在岩体力学中得到广泛应用，研究[12-14]表明离散元渗流演化的数值模拟结果与室内试验结果较吻合；TAN 等[15]采用UDEC 数值软件分析了完整花岗岩全应力-应变过程中渗透率的变化规律，发现拉伸微裂纹是引起渗透率增大的主要原因，并得到了体积应变与渗透率变化的线性关系。

综上可知，既有研究主要集中于岩石在全应力-应变下的渗流特性及渗透演化规律，但其研究对象多为完整岩体，而非含裂隙岩体，含注浆材料的裂隙岩体的研究更为少见。采用离散元方法可以从微观层面揭示渗流的内在机理，但是注浆之后的模拟研究较少。本文作者在室内三轴试验的基础上，采用UDEC 数值软件分析浆液填充对岩体渗透性能与力学性能的影响，进而从微观机理层面对复合岩体的渗透演化规律进行分析。

1 岩体注浆加固-渗透特性试验

1.1 试验概况

岩体通常是由岩石基体与裂隙组成，为减少岩石基体的影响，需采用渗透率较小的花岗岩作为试验对象。本文选用山东济南青花岗岩作为岩石基体，其渗透率低至1.4×10-20m2，平均密度为2 930 kg/m3，主要成分为石英、斜长石。试样为直径为50 mm、高度为100 mm 的标准圆柱体，并在其内部填充浆液，注浆材料选用P.O.42.5普通硅酸盐水泥浆液，其渗透率为7.9×10-17m2。试验采用不同充填厚度的光滑岩石裂隙壁，在2个岩石节理壁之间注入厚度分别为2，5 和8 mm 的水泥砂浆，分别命名为试样P2，P5和P8；再将注浆试样放在温度为20 ℃、湿度为95%的养护室养护28 d，然后将试样放置在蒸馏水中饱和24 h；最后，进行渗透测试试验。试验系统示意图如图1所示。

图1 注浆试验渗流测试系统示意图Fig.1 Schematic illustration of test system

为防止渗透过程中蒸馏水从岩样的侧壁通过，在复合岩体外侧用热缩管包裹，并在其上下端设置5道钢丝。试验中，岩体所受围压为5 MPa，以0.005 mm/s 的速率进行加载，当偏应力分别达到5，20 和40 MPa 直至峰值应力时，停止加载并进行渗透率测试。对于每一次渗流测试，试样上、下端的水压力分别为2.2 MPa和0.2 MPa，试样上、下端产生的2.0 MPa压力水头从高压力处流向低压力处；通过记录渗透压差随时间的变化关系，可以得到岩样的渗透率[2]：

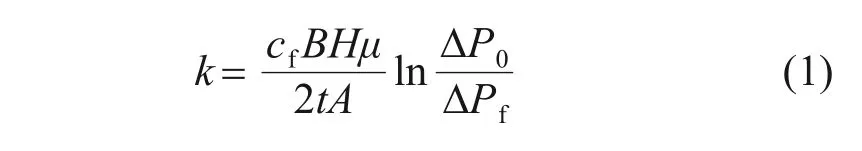
式中：k为渗透率；cf为水的体积压缩系数；B水箱体积；H为岩样高度；μ为水的动力黏滞系数；t为测试时间；A为试样的横截面积；ΔPf为试样的渗透水压差。本试验中cf=4.53×10-10Pa-1，B=175 cm3，H=100 mm，μ=1×10-3Pa·s，A=19.625 cm2，ΔP0=2.0 MPa，ΔPf=0.5 MPa。

1.2 试验结果

对于试样P5，在偏应力加载过程中，试样的渗透率、体积应变及偏应力随轴向应变的变化规律如图2所示。根据CAI等[16]的研究结果可知，当体积应变开始反向时，试样中的裂纹大量扩展，此时对应的应力为裂纹破坏应力；由渗透率的变化曲线可知，当偏应力低于裂纹破坏应力(135 MPa，图2中五角星所示位置)时，试样的渗透率先是小幅度减少，然后再缓慢增大，变化幅度较小；当偏应力大于裂纹破坏应力时，试样的渗透率快速增大，在峰值应力附近，试样的渗透率增大为初始渗透率的8.2倍。此外，试样的渗透率与试样体积应变的变化规律较相似。

图2 试样P5的渗透率、体积应变及偏应力与轴向应变的关系Fig.2 Relationship between permeability,volumetricstrain and deviatoric stress of sample P5 with axial strain

2 UDEC数值模拟分析

2.1 基于泰森多边形方法的UDEC模型

离散元程序UDEC 中的泰森多边形模型可用于岩石力学性质的模拟[17]；相比于PFC 离散元软件，UDEC中需要的材料参数更少，且各参数均有明确的物理意义，当块体间的应力超过抗拉或者抗剪强度极限值时，将产生断裂面，通过获取断裂面的信息，可以对岩石受力过程中不同阶段的裂纹演化进行分析[18]。

本文采用UDEC 对试样微观层面的渗透率演化规律进行分析，利用泰森多边形块体建立的复合岩样模型示意图如图3所示。块体的最小边长为1 mm，试样的中间部分为水泥砂浆材料，整个试样的块体均为不透水弹性材料，花岗岩与水泥砂浆的网格边长均为1 mm。模型的花岗岩区域包含4 595 个块体，33 883 个网格区，29 802 个接触；水泥区域包含520 个块体，3 824 个网格区，3 302个接触。花岗岩与水泥的弹性模量分别为Eg0和Es0，花岗岩块体间、水泥块体间及花岗岩与水泥块体间的接触采用摩尔-库仑模型，见图4。模型参数如法向刚度、剪切刚度、黏结力与抗拉强度均会对试样的宏观性质造成影响，当块体间的抗拉强度或者抗剪强度超过其极限值时，块体间的接触破裂，进而发生滑移现象，滑移过程中块体发生剪胀。正是由于块体的滑移与剪胀致使裂纹不断扩展，进一步在块体间形成渗流通道，因此，裂纹的扩展与岩体的渗透性密切相关。

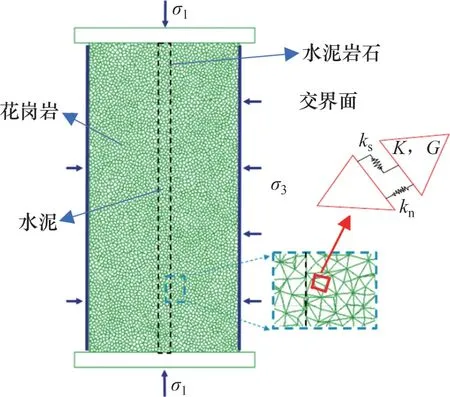
图3 试样P5泰森多边形块体模型示意图Fig.3 Schematic diagram of Voronoi model of sample P5

图4 块体接触模型[19]Fig.4 Block contact model[19]

块体的微观参数与真实参数有一定的区别，可以通过重现试样的宏观力学性质、破坏形式来确定其微观参数；通过一系列数值试验，最终得到适合本次模拟的微观参数，如表1所示。

表1 试样的微观参数Table 1 Microscopic parameters of samples

通过建立数值模型，得到不同充填厚度下试样P2，P5和P8(对应充填厚度分别为2，5和8 mm)偏应力随轴向应变变化的曲线，如图5所示。由图5可见：数值模拟结果与试验结果较接近，从而验证了数值模型的合理性。在偏应力峰前阶段，数值模型的应力-应变曲线与试验结果基本一样，但是在峰后阶段，二者存在一定的差异，试验中偏应力下降更明显，这与岩石的内部破裂现象有关，试验中，岩石的裂纹扩展可以发生在矿物颗粒内部，而模型的裂纹只能发生在接触间，因此本次模拟主要关注偏应力峰值前的应力-应变演变规律。

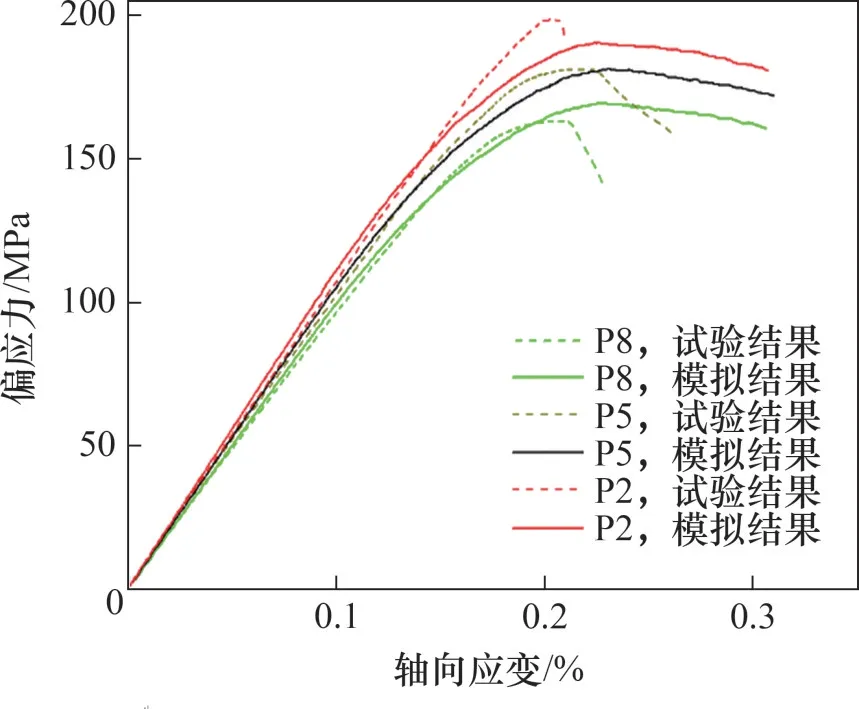
图5 试样偏应力-应变模拟结果与试验结果对比Fig.5 Comparison of simulated and experimental deviatoric stress-strain curve of samples

2.2 试样的渗透模拟

UDEC 模型中的渗流通过块体之间的空隙流动，其满足立方定律，当给定试样的等效水力宽度a，便可以通过式(2)求出渗流流量[15]。

式中：l为渗流路径长度；ΔP为渗透压力差。

由泰森多边形方法建立的试样模型的渗透性与初始设置的水力宽度密切相关，本文不考虑水力耦合作用，围压设置为5 MPa，试样上、下端的水力压差为2 MPa，试验过程中不断增加偏应力，直至达到目标值，在试样的上下端部施加压力水头进行渗流分析，保持试样的左右边界为不透水边界。当试样上、下端的压力差接近于0 MPa 时，停止试验，记录试样底端的流量，通过计算得到试样的渗透率。试样的水力参数如表2所示，流量变化如图6 所示。图6 中，Q为总流量；qˉ为通过裂隙的平均流量；n为裂隙数。通过设置的初始水力宽度，可以得到试样P5 的初始渗透率为2.99×10-18m2，与试验值3.03×10-18m2接近。

表2 试样的水力学参数Table 2 Hydraulic parameters of the samples μm

图6 模型的流量变化示意图Fig.6 Diagram of fluid variation in the model

3 UDEC数值模拟结果

3.1 渗流结果分析

渗透率随偏应力的变化规律如图7所示。由图7可见：在开始阶段，随着偏应力增加，试样的渗透率略有下降，因为当偏应力低于60 MPa 时，试样内部的原有的微孔隙会被压密(处于弹性变形阶段)，尽管水泥内部及胶结面产生少量的微裂纹，但试样的体积总体是压缩的，从而导致试样的渗透率减少；当偏应力为60～80 MPa时，试样的渗透率降至最低，近似为初始渗透率的1/2。当偏应力超过120 MPa时，试样进入弹塑性变形阶段，其渗透率开始增大；当偏应力达到峰值时，试样的渗透率增大为初始渗透率的10.4 倍，模拟结果与试验结果基本一致[9,20]。

图7 试样P5的渗透率随偏应力的变化Fig.7 Changes of permeability of sample P5 with deviatoric stress

为减少初始渗透率对试验分析的影响，对渗透率进行归一化处理(即将不同偏应力条件下的渗透率除以初始渗透率)，结果如图8所示。从图8可以看出：不同的充填厚度试样的渗透率随偏应力的变化规律较为类似，当偏应力小于60 MPa 时，因为试样受力压缩，试样的渗透率减小；当偏应为60～140 MPa 时，试样中有微裂纹发展，试样的渗透率呈现小幅度提升；当偏应力大于140 MPa时，试样的渗透率迅速增大，在偏应力峰值附近的渗透率平均值为初始渗透率的9.9倍。

图8 不同注浆厚度试样量纲一渗透率的变化Fig.8 Changes of normalized permeability of samples with different infilling width

3.2 体积应变与渗流关系

不同水泥砂浆充填厚度的试样的体积应变随轴向应变的变化如图9 所示，其中星形所示应力为裂纹破坏应力。从图9 可以得到体积应变开始增大时的偏应力，从而得到裂纹破坏应力，试样P2，P5和P8对应的裂纹破坏应力分别为145，135和126 MPa。

图9 试样渗透率和体积应变与轴向应变的关系Fig.9 Relationship between permeability and volumetric strain with axial strain

由图9可以看出：体积应变随轴向应变的演化规律与渗透率的变化规律基本一致，均呈现出先减小、后缓慢增大，超过裂纹破坏应力后再大幅度增大的趋势。试样中微裂纹的扩展引起了试样渗透率的变化，试样的体积应变可以看成微裂纹不断发展的结果，因此可以根据体积应变的变化规律预测试样渗透率的变化规律，这对于难以进行渗透率测试的试样是一种可行的替代方式。当偏应力小于裂纹破坏应力时，渗透率变化很小，近似为常数，故本文只对偏应力大于破坏应力时的渗透率进行拟合分析，得到不同注浆厚度试样的渗透率与体积应变的拟合方程，如表3所示，其中k为渗透率，εv为体积应变。随着注浆厚度增大，拟合方程的初始值(εv=0)不断增加，同时曲线的斜率也不断增大。

表3 试样的渗透率与体积应变的方程式Table 3 Equation between permeability and volume strain of samples

3.3 渗流发展

进行三轴试验时，由于实验仪器的限制，试验过程中并不能直观地看到渗流的发展过程，只能测试得到宏观渗透率，但由于注浆试样的复杂性，难以直接判断渗透路径；为了解试验过程中渗透的发生发展过程以及压力水头的产生过程，本文提取UDEC 的渗流发展过程，从微观层面分析注浆试样的渗透演化规律，结果如图10所示。

从图10 可知，当偏应力较小时(20 MPa)，岩石基体较为完整，岩石内部无流量产生，水泥浆的渗透率较大，水主要通过水泥浆流通；当偏应力增大到140 MPa时，水从水泥内部与岩石基体内的微裂纹处同时流动；当偏应力达到160 MPa 时，水主要通过岩石基体的连通微裂纹流动，通过水泥浆的水流量较少；当偏应力达到180 MPa时，水流量主要分布在岩石基体的连通微裂纹处。由此可知，当偏应力较小时，水主要通过注浆体流通，而当偏应力不断增大时，水主要通过岩石基体的连通微裂纹流通而不是通过水泥与岩石壁的交界面流通。

图10 试样P5在不同偏应力时的流量分布Fig.10 Flow distribution in different deviatoric stresses of sample P5

试样P5 在不同偏应力时的水压力分布如图11所示。从图11可知：当偏应力为20 MPa时，试样中的渗透水压力差从上至下呈现等梯度下降；当偏应力变为80 MPa 时，试样中间部位的水压力开始发生变化；当偏应力增大至160 MPa时，试样上部与中部的水压力发生明显改变；当偏应力增大到180 MPa时，试样上端水泥充填物处的水压力消散程度更大。

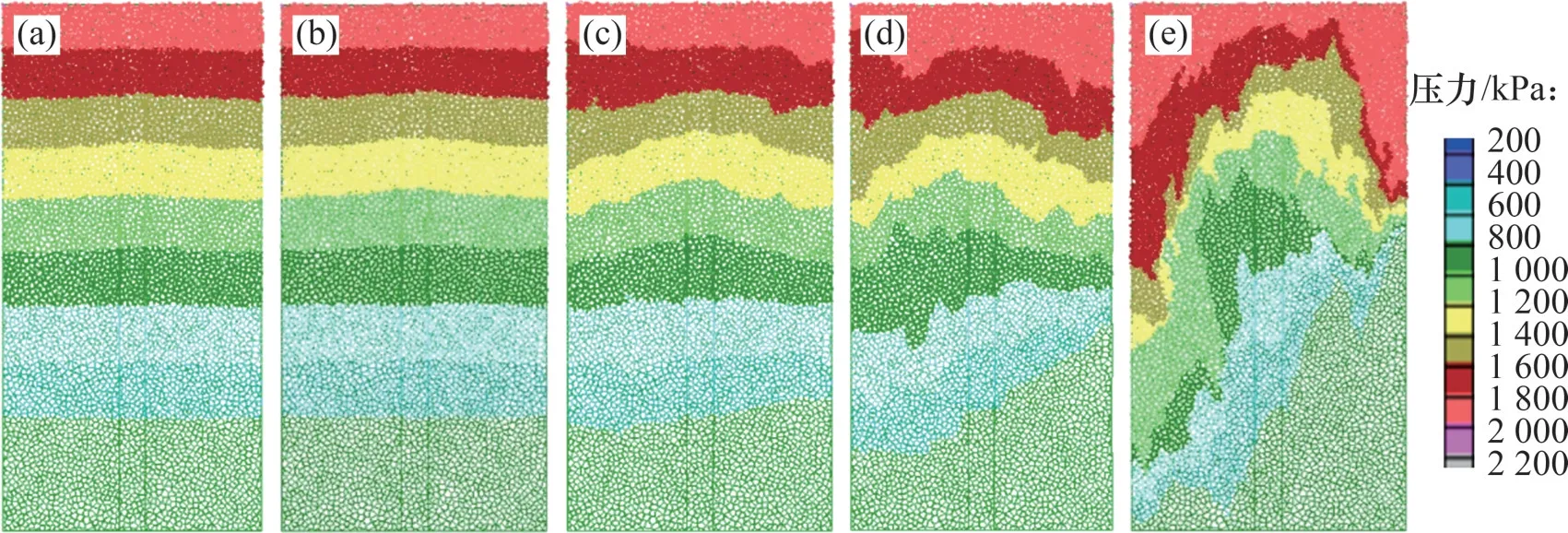
图11 试样P5在不同偏应力时的水压力分布Fig.11 Distribution of water pressure in different deviatoric stresses of sample P5

试样P5 在峰值应力时的渗流路径如图12 所示。由图12 可看出：大流量的水从岩石基体内的连通微裂纹处通过，在试样的左侧区域形成贯通的渗流路径(黑色箭头所示)；由试样的左端上部区域放大图可见，椭圆内部已经出现较多的分离块体(红色箭头所示)，但这些分离的块体内部并没有水流出现，由此可知只有试样内部形成贯通的裂纹，这些裂纹才会对渗流有较为明显的贡献。

图12 试样P5在峰值应力时的渗流路径Fig.12 Seepage passage of sample P5 at peak stress

3.4 微裂纹扩展

从3.2 节可知渗透率与体积应变呈线性关系，为进一步分析偏应力增大过程中试样微裂纹的发展程度，提取不同应力状态下的微裂纹分布，从微观机理上对试样的渗流现象进行分析，结果如图13所示。图13中，红色代表张拉作用引起的微裂纹，黑色代表剪切作用引起的微裂纹。

由图13 可知：当应力较小时，试样中基本没有微裂纹产生；当偏应力达到40 MPa 时，由于水泥的强度较低(只有花岗岩强度的1/10)，在水泥浆区域及水泥与岩石交界面处产生较多的剪切微裂纹；当偏应力增大到80 MPa 时，水泥内部几乎布满剪切微裂纹，在岩石内部也出现零星分布的剪切微裂纹与张拉微裂纹；当偏应力达到140 MPa时，在试样内部布满剪切微裂纹；当偏应力超过160 MPa时，试样中的张拉微裂纹数急剧增加，峰值阶段的张拉微裂纹数量达到最大。

图13 试样P5在不同偏应力时张拉微裂纹与剪切微裂纹分布Fig.13 Distribution of tensile crack and shear crack of sample P5 in different deviator stresses

微裂纹的发展与偏应力的变化规律如图14 所示。由图14 可见：当偏应力较小时，试样中的剪切微裂纹数较多；当偏应力大于80 MPa 时，剪切微裂纹与张拉微裂纹数均以较快速度增加；当偏应力超过140 MPa时，剪切微裂纹数开始减少，张拉微裂纹数仍不断增大，而此时试样的渗透率也开始以较大幅度增加，说明张拉微裂纹数的增大对于试样的渗透率贡献作用更大；当偏应力接近峰值应力184 MPa时，试样的微裂纹总数趋于一定值(约为16 600条)。

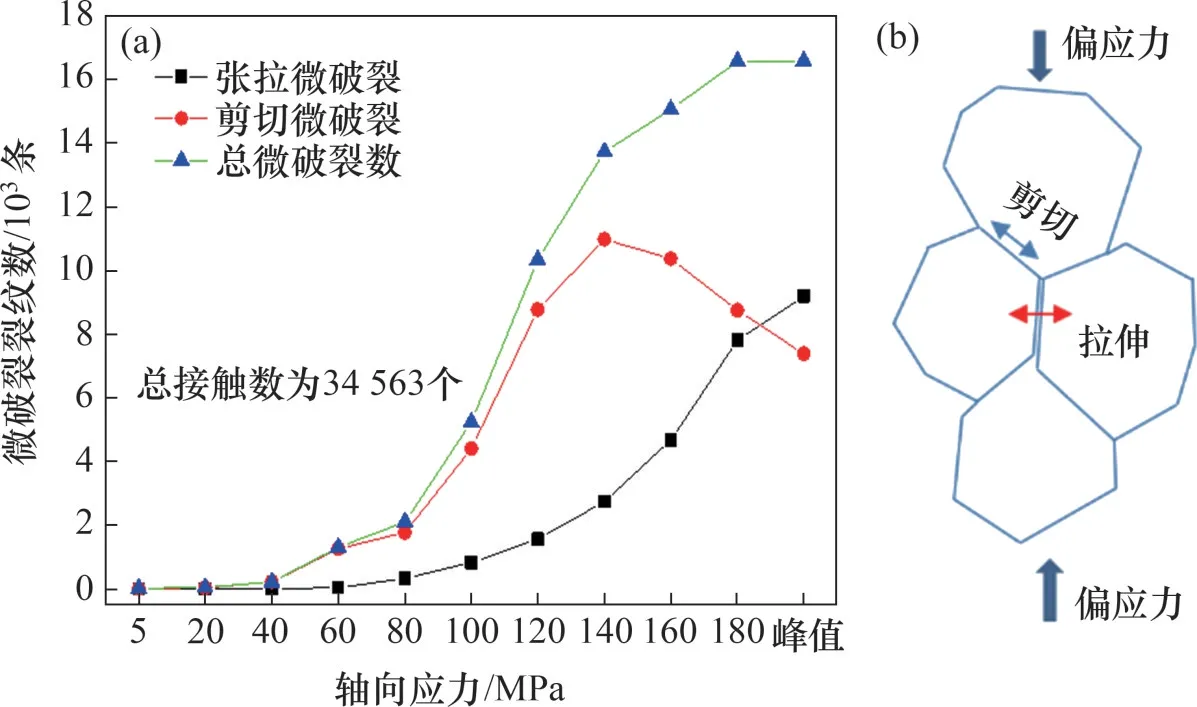
图14 试样P5在不同偏应力时微破裂的演化规律Fig.14 Evolution rule of micro-crack of sample P5 under different deviatoric stresses

4 结论

1) 采用UDEC 软件中的泰森多边形方法可较好地模拟水泥充填岩样的渗流演化规律，应力-应变、渗透变化规律及体积应变的模拟结果均与室内试验结果较接近。

2)随着偏应力增大，试样的渗透率先小幅度减小，之后缓慢增大，但当偏应力超过裂纹破坏应力时，渗透率大幅度增大，峰值应力时试样的渗透率急剧提升，平均峰值应力对应的渗透率为初始渗透率的9.9倍。

3)试样的渗透率与体积应变存在较强的线性关系，通过拟合方程可以快速计算出试样的渗透率。

4)当偏应力较低时，水泥内部的剪切微裂纹较多，压力水头主要通过水泥内部发生渗透；而当偏应力接近峰值应力时，试样中的张拉微裂纹较多，此时压力水头主要通过岩石基体内的连通微裂纹通道产生渗流作用。