基于改进的SSA-RBF的高频地波雷达海杂波抑制方法研究
杨 童,尚 尚,刘 明,张先芝,戴圆强
(江苏科技大学 电子信息学院, 镇江 212100)
高频地波雷达(HF surface wave radar)是一种新型海洋探测雷达,具有超视距环绕传播特性,可以沿着导电海洋平面低衰减传播电磁波还不受地球曲率限制,因此,凭借其超距离探测、全天候、实时精准等优势在海上作业、气象监测、民用商业等方面都起到比较重要的作用.高频地波雷达在对海面移动目标进行探测时,其辐射的高频电磁波会与海浪发生谐振,使得回波中夹杂大量的海浪散射干扰信号,即海杂波,其主要分量是一阶回波,而一阶海杂波在洋流切变的影响下其尖峰会出现频谱分裂,干扰海面目标的有效检测.因此,海杂波的有效抑制对雷达目标检测来说是非常必要的.
目前,国内外许多学者都相应提出许多海杂波抑制方法,主要有分形类[1-3]、子空间分解类[4-6]、对消类[7-9]、非线性预测类[10-12].分形类方法会在海情多变时容易出现目标和海杂波分形差异不显著,这可能导致目标检测效果不理想.子空间分解类方法中海杂波奇异值不能保证一直比目标的奇异值大,单纯将大奇异值部分进行置零,可能造成海杂波抑制不完全的问题.循环对消类方法对消次数的选取一定程度上限制了该算法应用,目前参数的设置还是根据以往经验,若选择不当可能引起目标被误消.随着神经网络的日益成熟,越来越多的学者将神经网络引入到对海杂波内在特性的研究中.文中采用非线性预测类方法,即在混沌理论基础上采用径向基函数(radial basis function,RBF)神经网络建立海杂波的预测模型,实现海杂波精准抑制.
网络的初始参数选取对网络模型的收敛速度和精度有一定影响,需采用优化算法来对RBF的初始参数进行优化,使得海杂波预测和抑制取得更好效果.麻雀搜索算法(sparrow search algorithm, SSA)由于收敛速度快、需要调整的参数少的优点已被应用于无人机航迹规划领域中,但是算法本身还具有许多缺陷,因此一些学者提出了相应改进策略.文献[13]将正余弦算法引入到跟随者位置更新来降低陷入局部最优的可能性,并采用高斯游走来避免算法停滞.文献[14]在发现者位置更新中提出自适应权重,平衡SSA开发和探索能力.此外,将柯西变异和反向学习结合对最优解进行干扰,进一步增强全局搜索能力.然而,上述的改进策略在一定程度上减低陷入局部最优的概率,但是,在应对高维复杂的问题时,算法的表现效果不佳.
针对上述讨论,提出了一种基于改进SSA-RBF(improved SSA-RBF,ISSA-RBF)海杂波抑制算法.改进后的麻雀搜索算法寻优效果优于粒子群算法(particle swarm optimization,PSO)和麻雀搜索算法(SSA),能够有效的优化RBF神经网络.把优化算法寻到的最优解还原成RBF初始参数,再用海杂波训练样本训练网络模型,实现RBF对海杂波内在特性的学习,进而达到海杂波有效预测和抑制的目的[15].采用实测数据进行仿真,结果表明与传统RBF神经网络和粒子群优化的RBF相比,ISSA-RBF海杂波预测精度和抑制效果都更好.
1 麻雀搜索算法及改进
1.1 麻雀搜索算法
SSA是从自然界麻雀觅食和逃避捕食者行为衍生出来的优化算法.整个觅食行为是在发现者-跟随者基础上叠加了侦察预警机制.种群中适应度值比较好的个体作为发现者优先获取食物,加入者跟随发现者进行觅食,同时选取一定比例的麻雀负责察觉危险.SSA通过计算每只麻雀的适应度值并排序,不断更新发现者、加入者、警戒者位置,使得所有个体向适应度最小的位置逐渐靠近,最终获得食物的最优位置.
种群中适应好的个体作为发现者更容易探索到最佳位置.发现者在大规模搜索找到食物后为种群中其余个体指导靠近食物的方向.发现者每次迭代位置更新公式为:
(1)
式中:α为(0,1]之间的随机数;itermax为最大迭代次数;Q是服从标准正态分布的随机数;ST∈[0.5,1];L表示大小为1×d,内部所有元素为1的矩阵;R2和ST分别为麻雀的预警值和安全阈值.
加入者位置更新公式:
(2)
侦察者位置更新公式:
(3)
式中:β为服从标准正态分布的随机数,负责调整步长;K为[-1,1]的随机数;fi为当前麻雀的适应值,fw和fg分别为当前全局最大和最小的适应度值;ε是最小的常数,以避免分母为零.
1.2 改进麻雀搜索算法
1.2.1 混沌精英反向学习
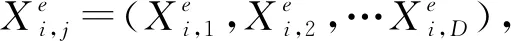
(4)
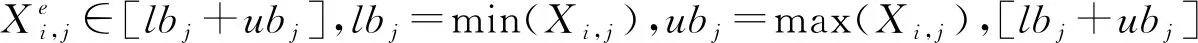
(5)
由于麻雀搜索算法迭代后半部分种群多样性迅速下降,易发生跳不出局部最优的问题,文中提出基于Tent混沌映射精英方向学习策略,在Tent映射基础上利用精英个体比普通个体的反向解更大概率靠近全局最优解的这一优势来初始化种群.改善了SSA的种群多样性,使得搜索空间初始解的分布更具有遍历均匀性,这对算法的寻优效果大有裨益.
1.2.2 自适应变异
以一定概率Pm对当前最优解进行自适应变异并进行贪婪选择,比较变异前后的适应度大小,若变异后个体的适应度值小于变异前,则接受变异.自适应变异概率Pm动态变化过程描述为:
(6)
式中:ts为最优解不发生变化的迭代次数;Pm∈[0,0.9],当3 (7) 式中:Titeration为最大迭代次数;D为麻雀个体维数. 计算前后两代最优解之间的差值以判断最优解随着迭代次数增加有无变化.通过如下公式进行判断: (8) 式中:Xbestt和Xbestt-1分别为前后两代的最优值,通过两者差值K是否为零,判断ts是增加1还是清零.自适应变异借鉴多元宇宙优化算法中物质交换思想产生新的位置为: (9) 式中:Xmutate(t+1)为变异后的个体;p1为[0,1]之间的随机数.对变异个体进行贪婪选择: (10) 式中:Xbest(t+1)为全局最优解;Xmutate(t+1)为变异的个体;rand为[0,1]之间的随机数. 当rand 图1 改进后的ISSA流程Fig.1 Improved ISSA flow chart 文中选用6个测试函数,包括单峰函数F1~F3、多峰函数F4和固定维度的多峰基准函数F5~F6来评估ISSA算法的性能.测试函数的维度、范围、最优值等基本信息见表1,将ISSA性能与粒子群、GWO和原始的SSA进行对比. 为保证实验的公平性,设定最大迭代次数和种群数量分别为500和30.将每个基准函数独立运行30次,通过最优值、平均值和方差这3个指标来反映算法寻优效果.图2为4种算法收敛曲线的对比.从图2可以看出,对于F1~F6测试函数ISSA的收敛速度和求解精度都优于其他对比算法. 表1 测试函数 图2 测试函数收敛曲线Fig.2 Test function convergence curve 表2给出ISSA与其他算法针对6个函数的测试结果,ISSA在优化F1~F3函数时,其平均值和标准差均更小.对于F4来说,ISSA算法的性能与SSA算法相同,但比粒子群和灰狼算法要好的多.在求解固定维度的多峰函数时,ISSA的平均值更接近于理论值,而且标准差明显小于其他算法.实验结果证明,ISSA在保证精度的情况下收敛速度较快,同时显现较强的稳定性. 表2 测试函数优化结果 海杂波是多变量非线性系统,若要分析其内部所有状态参量的信息,就需要将采集的一维海杂波序列扩展到高维空间中,即相空间重构[17].海杂波预测方程为[18]: xi+mτ+1=F(xi,xi+τ,…,xi+mτ) (11) 式中:m和τ为相空间重构的参数,分别为嵌入维数和时间延迟. 获得海杂波预测方程表达式需要借助神经网络强大的学习能力对其进行建模,来完成对预测方程的学习估计,文中选用RBF训练海杂波样本数据来完成这一估计任务.首先把采样的海杂波混沌序列构造出k个m×τ维的训练样本,将其输入RBF神经网络经过隐含层高斯核函数的映射和输出的加权求和得到相应输出.通过k组数据训练之后得到海杂波预测关系式: Yi=f(Xi) (12) 为确保预测具有一定的精度,采用一步预测的方式,则网络的预测值为: (13) 网络初始参数是网络模型收敛速度和精度的关键因素,因此引入ISSA对RBF的3个初始参数wk,ck和σk进行优化.对获得最佳初始参数的RBF网络进行训练,直到达到预定的预测精度或者最大迭代次数时停止训练,得到ISSA-RBF 海杂波预测模型.由于不同距离单元的海杂波都具有混沌特性,故选用一个距离单元的海杂波训练得到预测模型来对相邻距离单元的海杂波进行预测.定义平均补偿率ρ对预测精度进行计算: (14) 式中:err(n)为预测值和海杂波理论值之间的差值;xn为海杂波样本的观测值;var(·)表示方差. 由于同一海域不同距离单元的海杂波内在动力学规律相似,可用其中某一距离单元得到的预测模型去预测相邻距离单元的海杂波.之后从含有目标的雷达回波中减去预测的海杂波,进而达到提高目标检测性能的目的.建立的RBF海杂波预测模型,因为目标和海杂波混沌特性差异而只能预测海杂波,将目标保留下来,避免了其他抑制算法将目标误消的情况[19].海杂波抑制效果用信杂噪比来评价: (15) 式中:Ps,PcPn分别为目标信号,杂波和噪声的功率. 文中高频雷达回波数据来自威海测量的实测数据,雷达的工作频率是3.7 MHz,测试环境为Inter(R) Xeon(R) CPU E5-2450,2.10 GHZ,32GB内存,Windows10 64位,为了减少计算量,加快网络收敛速度的需要,在构建海杂波训练集前将海杂波做归一化处理.将提纯的第31个距离单元的海杂波数据构造训练集,500组训练样本进行800次迭代,精度为0.000 1,对RBF神经网络进行训练.通过C-C方法计算得出海杂波时间序列的时间延迟τ=3,嵌入维数m=4.综合考虑复杂度和精度等因素,隐含层设置为5,故RBF的网络结构为12-5-1. 为提高网络收敛速度和精度,在训练网络之前采用PSO、SSA和ISSA 3种优化算法来优化RBF,通过500组数据和参数调整最终训练得到较好的海杂波预测模型.从图3均方误差曲线可以看出,未改进的SSA-RBF相对于PSO-RBF没有显著优势,经过上述改进策略后ISSA-RBF均方误差曲线明显小于其他算法.当迭代次数最大时,其均方误差值达到0.053 94,因此ISSA-RBF模型训练得到的预测模型效果最优. 将训练好的海杂波模型对无目标的第30个距离单元的海杂波进行预测,为进一步比较神经网络模型预测的效果,将实验信息在表3列出. 图3 均方误差曲线Fig.3 Man square error curve 表3 训练模型和预测的实验结果 从表3可以看出,ISSA优化算法收敛时间最短是51.34 s,并且适应度值最小,以最短的时间获得最佳的初始参数,为网络模型训练奠定基础.ISSA-RBF预测性能均高于其他模型,证明改进的麻雀搜索算法优化RBF网络初始参数效果更好.ISSA-RBF的预测精度相比未优化的网络模型增长4.1%,已高达96.1%.精确预测海杂波,对后面抑制海杂波具有重要意义. 在第30个距离单元分别加入一个远离和靠近海杂波的模拟目标,目标的多普勒频率分别为0.5和0.059 Hz.利用ISSA-RBF模型来预测和抑制含有模拟目标的雷达回波中的海杂波.将预测的海杂波与原始回波相减便得到海杂波抑制后的高频地波雷达的回波数据,图4为海杂波抑制前后与循环对消算法的效果对比. 图4 海杂波抑制效果对比Fig.4 Suppression comparison effect graph of sea clutter 从图中看出循环对消抑制算法都将目标信号误消,而文中算法抑制后海杂波的幅度降低到与背景噪声的幅度接近,且将目标保留下来.目标远离和靠近海杂波时,信杂噪比分别提高了5.84 dB和4.91 dB.少了海杂波的影响,目标凸显出来,雷达对目标的检测性能将得到大幅提高. 为抑制高频地波雷达回波中的海杂波,提高目标检测性能,提出一种改进的SSA-RBF的高频地波雷达海杂波抑制方法,借助RBF神经网络学习海杂波的动力学规律,建立海杂波预测模型,进而完成对临近距离单元海杂波的预测和抑制.为优化网络性能,ISSA提出混沌精英反向学习初始化种群,改进侦查预警向最优解跳跃的更新方式,自适应变异等一系列改进.改进后的SSA用测试函数验证得出,ISSA算法的收敛速度的精度都优于其他对比算法.就预测效果来说,ISSA-RBF的预测精度达到96.1%.最后将预测的海杂波从雷达回波中减去实现海杂波抑制,模拟目标远离海杂波时,抑制前后信杂噪比提高5.84 dB,靠近时提高了4.91 dB.综上所述,ISSA-RBF对海杂波抑制效果与其他模型相比具有一定的优越性,对雷达目标检测有重要意义.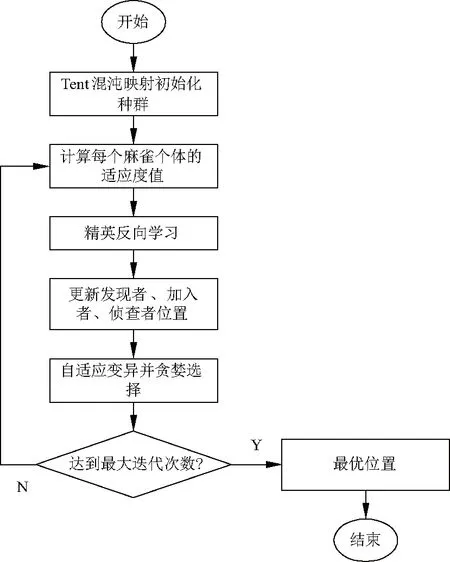
2 ISSA算法的性能测试

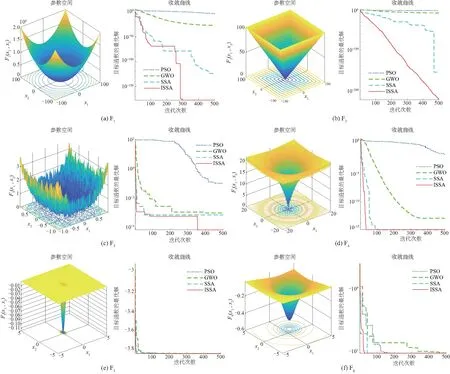
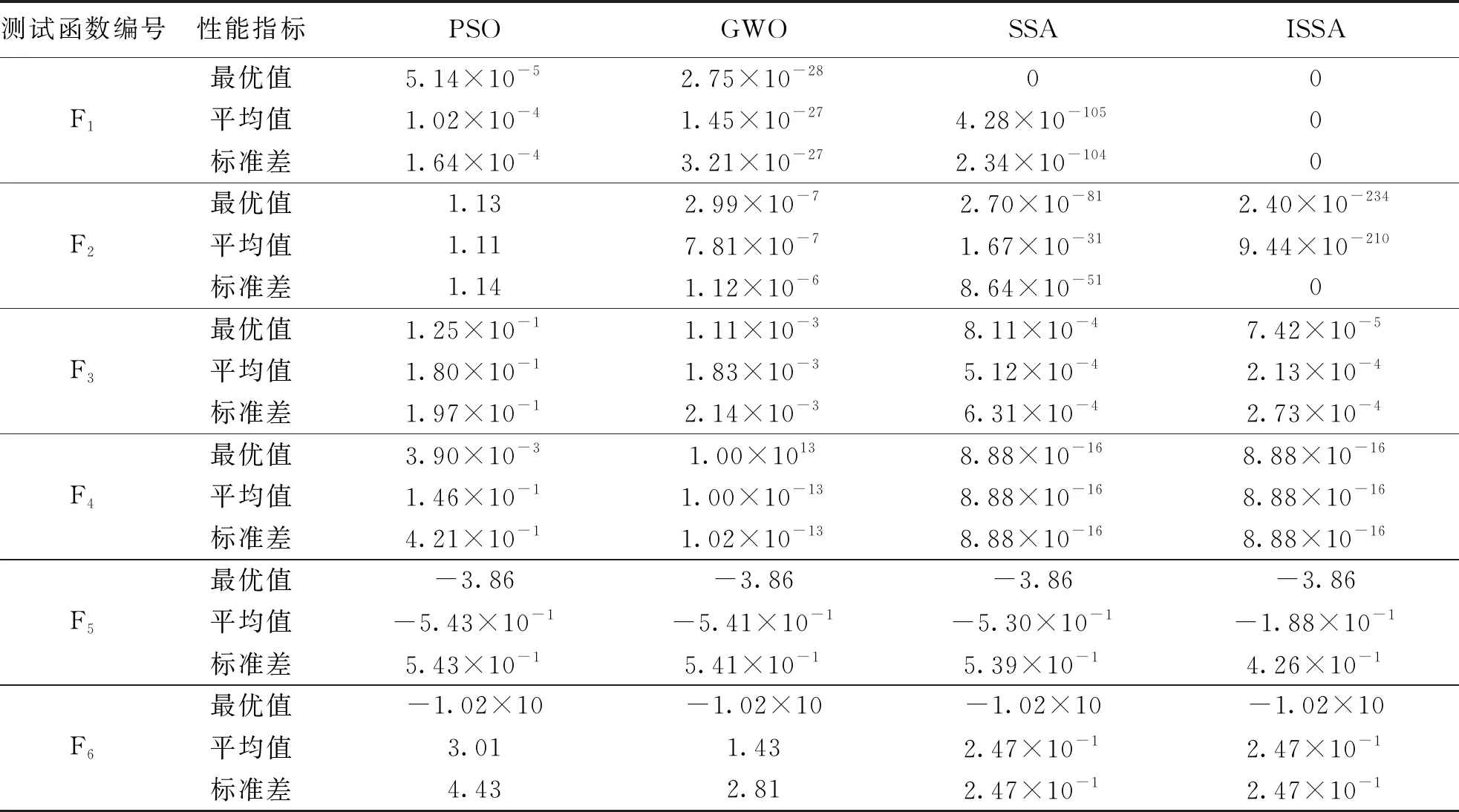
3 海杂波预测及抑制
3.1 海杂波预测
3.2 海杂波抑制
4 实验结果和分析
4.1 海杂波预测实验结果分析
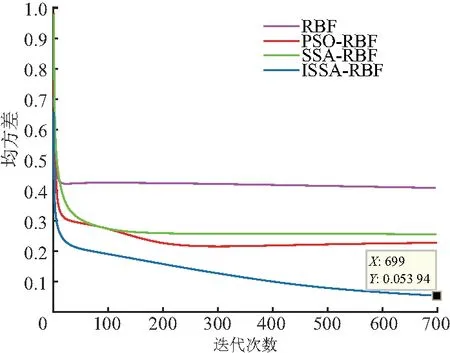

4.2 海杂波抑制实验结果分析
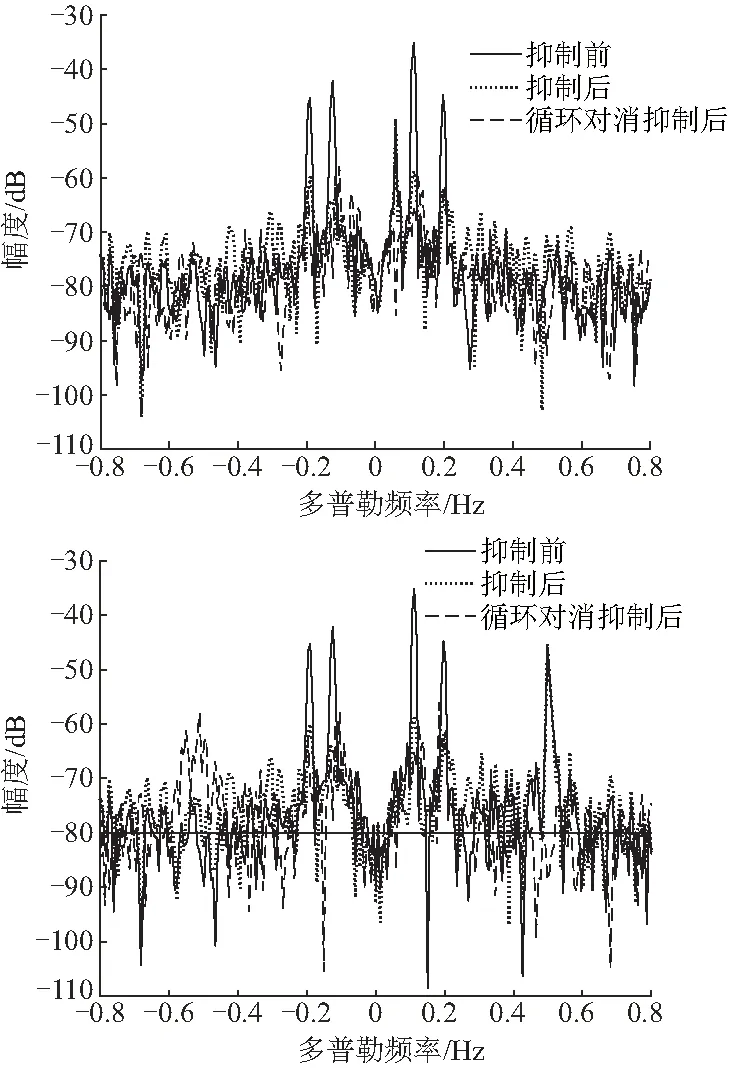
5 结论

