基于Dubins曲线的局部路径规划方法研究
李胜琴,闫祥伟
(东北林业大学 交通学院,哈尔滨 150040)
0 引言
近几年,无人驾驶技术逐渐成为研究热点。无人驾驶技术是系统性问题,主要涉及环境感知、高精度定位、运动预测、车辆控制和路径规划等。要使传统汽车具备全场景的无人驾驶能力,不仅需要保证各个模块功能的正常,更需要各模块之间的协调。所以至今全场景的无人驾驶技术仍处在研发测试阶段,而针对封闭园区、矿区和港口等特定场景,无人驾驶技术已相对成熟。其中矿山智慧化已成为当前采矿业发展的重要趋势。在整个智慧矿山系统中,矿区车辆的路径规划是关键问题之一。路径规划分为全局路径规划与局部路径规划,全局路径由云平台下发到车端,而局部路径的规划则由车载计算平台实时计算产生。在无人自动驾驶系统中,路径规划是关键环节之一,上游承接感知模块,下游承接控制模块,其负责在真实的道路环境中,按照既定的约束条件(如无碰撞、路程最短和时间最短等)寻找一条从开始位置到目标位置的最优路径[1-2]。
目前路径规划按不同算法可分为图搜索类算 法[3-4]、采样类算法[5-6]和人工势场类算法[7-9]等,不同的算法适用的范围都有所不同。冯凯等[10]在基于无人驾驶高精度地图的基础上,通过 A*算法进行了全局路径规划的设计与实现,但此方法需要在已建立的高精度地图基础上实现,对于结构化道路场景,无法满足实时规划。李全勇等[11]提出了改进的Dijkstra 算法,引入路径平滑度,以时间权重为优化目标求解最优路径,但其并没有考虑障碍物距离权重对规划结果的影响。刘冰雁等[12]改进了人工势场函数,调整势场作用区域,构建了以远距点斥力忽略、障碍点引力减弱的综合势场模型,解决了传统人工势场法容易陷入局部极小值的问题,但是并没有对生成的轨迹点进行优化处理。孙上杰等[13]针对强化学习算法收敛速度慢,易产生“维度灾难”的问题提出一种深度学习与强化学习相结合的算法,用于解决6足森林消防机器人的路径规划问题。唐文秀等[14]对于移动机器人立体视觉导航的全过程进行研究,分析立体视觉测量信息到真实三维景物信息的计算、人工势场法进行路径规划这两项关键技术。Shkel等[15]提出基于 Dubins路径的分类方案,能够在有方向约束的2点直接找到最短路径的方法,该方法不需要显式计算候选路径,在实时性上可以满足无人车实时路径规划。
本研究针对矿区场景,基于Dubins曲线,提出一种无碰撞、平滑的局部路径规划算法。通过选取Dubins集合中的4种曲线类型,计算预选路径集合,然后建立车辆可行域模型,对预选路径集合做碰撞检测,提取无碰撞的路径,之后基于分离轴理论,对无碰撞的路径做精确的碰撞检测。并设计评价函数,在无碰撞的路径集合中,结合规划中的影响因素,求解目标路径。最后利用B样条曲线对生成的轨迹做平滑处理,从而获得一条相对最优的局部路径。
1 基本问题描述
矿区的场景相对公开道路场景,道路信息较为多变。矿区的道路随着“采”“排”作业的进行会不定期发生变化,尤其是采掘面和排土场变化频率很大,云平台进行全局路径规划后,矿卡按照路径任务进行循迹行驶,在采掘面和排土场,或者前方存在障碍物需要绕行时,矿卡根据信息决策模块输入的信息,对可行驶区域进行局部路径规划[16]。矿卡在采掘面和排土场的局部路径规划上的问题,可以描述为在目标路径与起点之间规划一条局部最优路径的问题,其中目标路径是由云平台全局路径规划产生,由n个等距的点p(x,y,θ)描述,点之间的间隔为0.2 m,如图1所示,θ为目标路径上轨迹点的航向。图1中的无人驾驶车辆路径规划问题可以归纳为:在已知周围障碍物信息、目标路径信息和车辆参数信息的条件下,求解起点到目标路径点的路径,且该路径须满足车辆运动约束、无碰撞、路径平滑的条件。
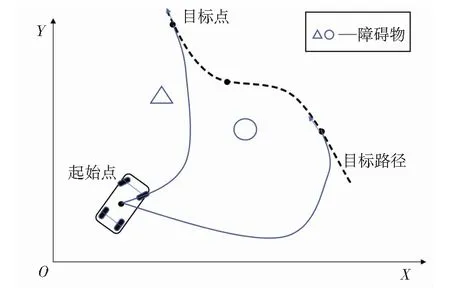
图1 场景描述Fig.1 Scene description
Dubins曲线的路径集合D={LSL,RSR,RSL,LSR,RLR,LRL},包含平面内2个指定运动方向的点之间的最短路径[15]。其中,L表示沿逆时针方向的圆弧路径段;R表示沿顺时针方向圆弧路径段,S表示沿直线运动。图2为D集合中的一种,pi(x0,y0,α)表示初始位姿,pf(x1,y1,β)表示目标点位姿,两圆半径r相等,其中α、β是起点与目标点切线方向与X轴的夹角。

图2 RSL曲线Fig.2 RSL curve
Dubins曲线有6种类型,如图3所示。其中RLR、LRL曲线类型,由于不包含直线路段且圆弧路段曲率过大,使得无人车控制难度增大。在轨迹跟随过程中,应尽量避免大曲率的路径出现,防止在跟随路径的过程中,出现横向偏差过大情况。所以在计算路径时,仅需要求解LSL、RSR、RSL、LSR这4种曲线,再从中选取满足约束的路径作为最优解。

图3 Dubins曲线类型Fig.3 Dubins curve
2 基于Dubins曲线的路径规划方法
2.1 路径求解
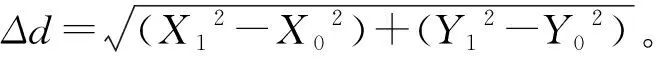
α=γ-θ。
(1)
β=δ-θ。
(2)
(3)
(4)
式中:γ和δ分别为起点、终点与X轴的夹角。通过公式(4)单位化,将转弯半径单位化r= 1,这样处理可简化后续的计算工作。为了简化路径的求解,引入3个算子[13]Lv(x,y,φ)、Sv(x,y,φ)、Rv(x,y,φ)。
(5)
式中:v为在L上所经过的路径长度;φ为在曲线上经过的弧度;x、y为在旋转后的坐标系中路径点的坐标。建立Rq(Sp(Lt(0, 0,α))) = (d,0,β)等式关系,将上述算子带入,则有如下关系式。
pcos(α+t)+2sin(α+t)-sinα-sinβ=d。
(6)
psin(α+t)-2cos(α+t)+cosα+cosβ=0 。
(7)
α+t-q=β{mod 2π}。
(8)
联立式(5) (6) (7)可得到L的隐式解
(9)
(10)
(11)
则L=α-β+2t+p。

图4 求解RSL型Dubins曲线Fig.4 Calculate RSL Dubins curve
同理可求得LSL、RSR、LSR的路径长度L,这里不再赘述。将L反归一化,则可得到目标路径长度。
上述求解的结果为路径集合,其中每一条路径由圆弧和直线组成。对于点对点可能产生的若干种行驶路径,设计损失函数如下
cost=wc×t+ws×p+wc×q。
(12)
其中wc和ws表示曲线段和直线段的权重。通过对比路径集合中每一条路径的损失函数值,筛选出cost值最小的路径。该路径作为备选路径,再进行反求得到路径点,作为碰撞检测的输入。
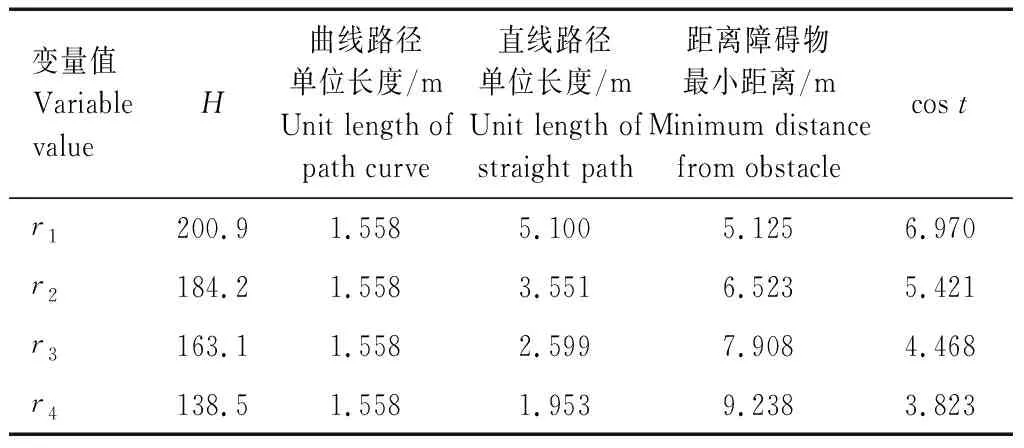
设计图5的规划场景,该场景包含一条真实的目标路径以及规划的起始点,起点的GPS坐标为(41.802 924 5,109.994 822 1,337.913)。目标路径上的轨迹点作为规划的终点,并设置4种车辆的转弯半径作为算法的输入参数,即转弯半径r1、r2、r3、r4分别为16、21、26、31,对上述算法进行验证。

图5 规划场景Fig.5 Scene of planning
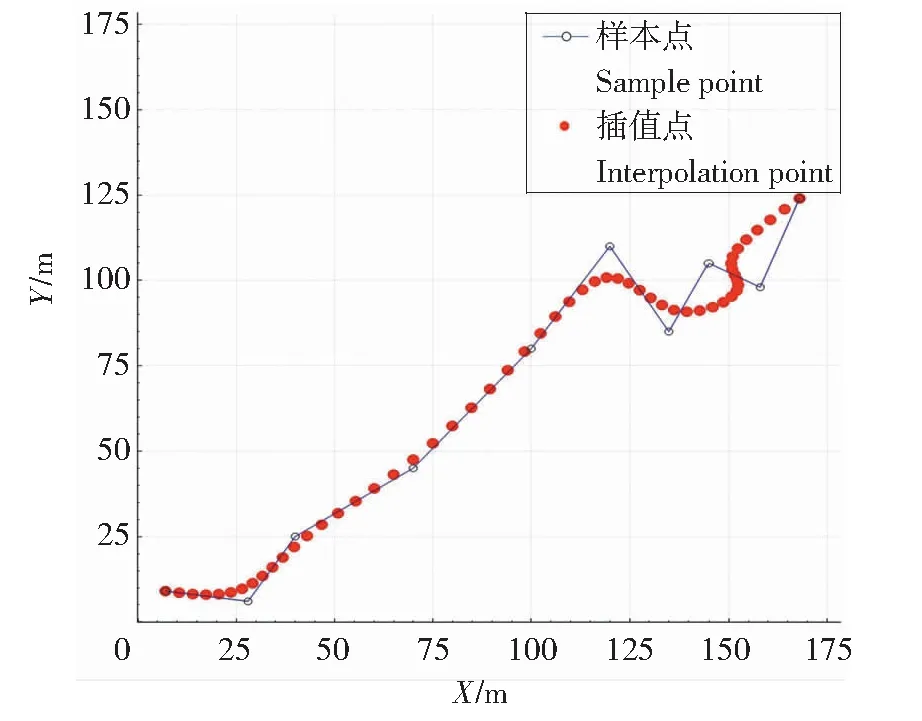
由图5可以看出,灰色的多边形表示4个静态障碍物,十字交叉线段的交点表示设置的规划起始点,长边的指向为起始点的航向(与正北方向的夹角)。选取目标路径上一点,坐标为(14.393 9, 103.905 0)索引为14。以半径r3为转弯半径,将设置好的参数输入到编写的算法程序中,得到表1中的结果。

表1 成本(cost)值与路径参数Table1 Value of cost and path parameters
表1的数据表明,当成本即损失函数(cost)值最小时,计算的总路径长度最短,曲线路径长度最短。验证了本研究设计的损失函数可以有效地从Dubins解集中初步筛选符合期望的路径,减少后续碰撞检测的数据量,提高算法的运行效率。
2.2 轨迹点求解
轨迹点由p(x,y,ε)表示,其中ε表示每一个路径点的航向,x和y表示轨迹点在车体坐标系中的坐标。设置起点pi(0,0,α)= (0,0,π/2)。取每个路径点(xpi,ypi)之间的距离为0.2 m,则L=0.2×i,其中i表示路径点的索引。在计算路径轨迹点之前,首先需要计算p段的起点p1(x1,y1,θ1)和终点p2(x2,y2,θ2)。
(13)
(14)
将L归一化,以便于轨迹点的求解。
(15)
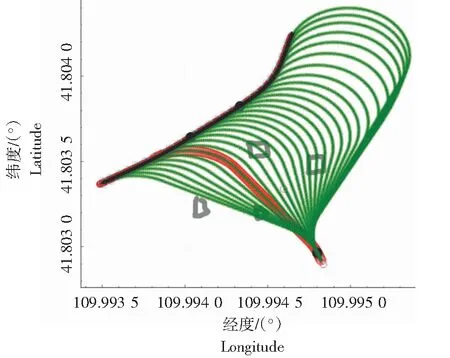
当l (16) 当t (17) 当t+p (18) 将点p(x,y,ε)反归一化,则可得到路径上的轨迹点,如图6所示。 图6 规划结果Fig.6 Result of planning 前文计算的路径结果是在没有考虑环境中障碍物的条件下得到的。为了兼顾无人驾驶车的行驶安全性,对规划的路径进行碰撞检测,剔除可能与车辆发生碰撞的路径,保障智能车辆行驶的安全。出于提高碰撞检测算法效率和准确性的考虑,将碰撞检测算法设计为分层检测。首先将无人驾驶车周围环境中的障碍物依次输入到可行域中进行判断,忽略不在可行域范围内的障碍物。然后对可行域范围内的障碍物进行精确地碰撞检测,如果发生碰撞,则更改路径,重复上述步骤,直至找到无碰撞的安全路径。设计的无人驾驶车可行域模型,仅需要障碍物与无人驾驶车之间的距离,即可初步判断是否会与车辆发生碰撞。对于可能发生碰撞的障碍物,基于分离轴理论对其进行精确碰撞检测,进一步判断障碍物是否影响无人驾驶车的行驶安全。 无人驾驶车可行域模型基于车辆单轨运动学模型[17]建立。无人驾驶车可行域模型如图7所示。图7为当θ>0时的可行域模型。 (19) (20) (21) (22) (23) (24) (25) 式中:Rl和Rr分别为车辆左右两侧最小转弯半径;lm表示车辆后视镜的长度;dr为车辆尺寸的膨胀值。 图7 可行域模型Fig.7 Vehicle feasible region model 图7中三角形表示障碍物,位置为Q(xp,yp)。O1(xo,yo)为转向圆心。则车辆的可行驶域为[xl,xr]。 (26) 当xl≥xp+dp/2或xr≤xp-dp/2时,障碍物不在车辆可行域内,不需要考虑该障碍物。dp为障碍物的多边形包围盒在坐标系YOX的X轴上的投影。 通过建立无人驾驶车可行域模型,可以仅通过障碍物距离无人驾驶车的纵向距离,快速地排除掉不需要进行精确碰撞检测的障碍物,提高算法运行效率。筛选出的危险障碍物输出到分离轴碰撞检测算法模块,再进行精确的碰撞检测。 碰撞检测的目的是检测车体的凸多边形与障碍物的凸多边形之间是否发生交涉[18],而分离轴(SAT)定理是一种被广泛使用于凸多边形碰撞检测的技术,该理论仅通过基本的数学向量计算,就可以判断2个凸多边形是否相交,计算速度快且准确。将车辆与待检测障碍物抽象为AABB多边形包围盒,进而对车辆可行域内的危险障碍物进行分离轴检测,判断与车辆是否发生碰撞。 车辆与障碍物之间的分离轴检测如图8所示。以障碍物多边形ab边的垂线为分离轴,分别将车辆多边形与障碍物多边形投影到分离轴上,得到两多边形的投影线段,判断投影线段是否重合。当两多边形所有边的检测结果都重合时,表示两多边形发生碰撞。碰撞检测算法的流程如图9所示。 图8 碰撞检测Fig.8 Collision detection 图9 碰撞检测算法流程Fig.9 Collision detection process 通过遍历前文计算的路径上每一个轨迹点,在每一个轨迹点上对无人驾驶车辆与障碍物进行分离轴检测,则可快速地判断所规划的路径是否安全可行。 本研究所提算法的目标是在已知起点和目标路径以及周围环境信息的条件下,快速地求解一条从起点到目标路径的无碰撞、易跟踪且能快速到达目标路径的局部路径。为了从路径集中筛选满足既定约束条件的局部最优路径,设计如下评价函数H。评价函数的设计,主要针对3个因素优化:无人车距障碍物的距离、无人车转弯半径、规划路径结果中曲线路径和直线路径长度。 (27) 式中:d为轨迹点距障碍物的最近距离,m;r为当前路径转弯半径,m;rmin为最小转弯半径,m;rmax为最大转弯半径,m;Lt、Lq分别为路径中曲线路径段t、q的长度,m;Lp为路径中直线路径的长度,m。 Dubins曲线由圆弧和直线组成,应用在路径规划时,符合无人驾驶车的运动特性,然而当无人驾驶车的转弯半径过小时,各曲线连接点处会出现不平滑的现象。为了使得规划的轨迹更加平滑,便于无人驾驶车跟踪轨迹,引入B样条曲线对轨迹进行平滑处理。B 样条函数曲线具有计算成本低、能够保证路径的连续性,且可以通过节点改变控制点来影响局部曲线等优点。在路径平滑性上具有明显优势[19-20]。 根据文献[21],二次均匀B样条曲线可表示为 (28) 式中:t∈[0,1];Ni,2(t)为B样条曲线的基函数;P0、P1、P2为3个轨迹点。 P(t)=(1-t)2P0+2t(1-t)P1+t2P2。 (29) 插值的轨迹点的航向方向与样条曲线上点的切矢指向相同。切矢由下式给出。 P′(t)=2P0(1-t)+2(P0-2P1+P2)t。 (30) 将2.2中求解的轨迹点带入公式(30),则可得到平滑后的轨迹点。通过B样条曲线平滑,可以消除轨迹点中突变较大、车辆无法跟踪的点,从而保证路径的曲率连续性。由图10可知,B样条曲线对平滑轨迹中不连续的点,有明显效果。 图10 B样条曲线平滑Fig.10 Smoothing trajectory by B spline curve 使用基于Qt编写的仿真软件验证本研究设计的算法,构建图5所设计的规划场景,进行局部路径规划,仿真结果如图11所示,其中红色路径即本研究所提算法计算出的相对最优路径。以目标路径中索引为16的轨迹点作为规划终点,使用本研究设计的评价函数H,对比不同转弯半径条件下的H函数值,则可从规划的结果中筛选出一条平滑、无碰撞、曲线路径长度短的局部最优路径。仿真结果数据(表2)表明,当H值最小时,总路径的长度最小,且到障碍物的最小距离以及转弯半径都是最大。 表2 仿真结果数据Table2 The data of simulation result 在目标路径中,采样28个轨迹点作为规划终点,仿真结果如图11和图12所示。从图11可以看出,在满足无人驾驶车行驶安全的前提下,红色的路径相对其他路径路程更短,曲率更小。该路径的H函数值为158.7,为计算结果中的最小值。 图11 最优规划结果Fig.11 The best result of planning 图12 评价函数H与路径点索引关系Fig.12 The relationship between the evaluation function H and the waypoint index 统计不同障碍物数量的条件下算法的运行时间,见表3。表3中的数据显示,算法运行时长基本处于20 ms左右,能够满足无人驾驶车的实时性要求。 表3 算法耗时数据Tab.3 The data of algorithm time-consuming 针对矿区采掘面和排土场的作业场景,提出基于Dubins曲线的局部路径规划方法。在Dubins曲线的理论基础上,建立车辆可行域模型,结合分离轴理论对预选路径进行碰撞检测,同时设计评价函数,从路径集合中筛选出满足约束的路径,并对该路径进行平滑处理,最终输出最优路径。在基于Qt软件开发的仿真软件中,针对所提规划方法的实时性与有效性进行仿真验证。通过对比场景中不同障碍物数量、算法的运行时间,验证了所提规划方法的实时性。统计不同转弯半径下评价函数值,证明了本研究所设计评价函数的有效性。由于引入了碰撞检测算法,克服了Dubins的间隔问题对路径规划的影响。 经仿真验证,表明所提的局部路径规划方法对解决矿区采掘面和排土场场景中的局部路径规划问题,在实时性与有效性上有显著效果,可以为该场景下的无人驾驶车局部路径规划提供理论和实践依据。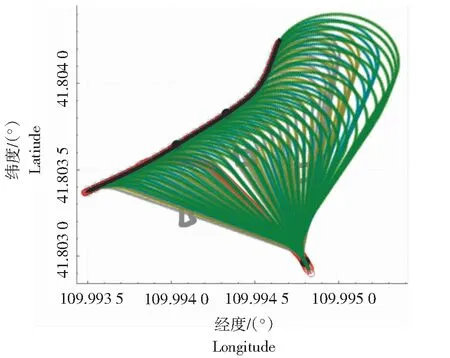
3 碰撞检测
3.1 无人驾驶车可行域模型建立
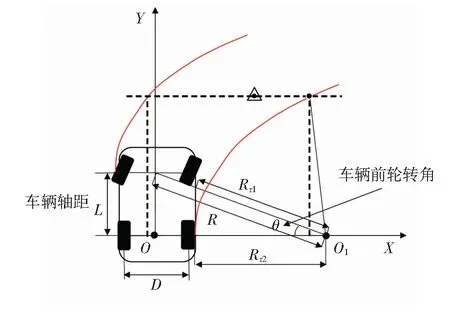
3.2 分离轴(SAT)碰撞检测


4 路径优化
4.1 评价函数
4.2 轨迹平滑
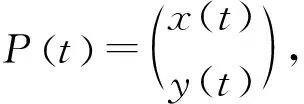
4.3 算法验证与结果分析


5 结论

