一字导流墩对弯道岔河进流调整的研究

于佳敏，陆伟刚，奚 望，周秉南

（扬州大学水利科学与工程学院，扬州 225009）

0 引 言

弯道岔河是天然河流及人工河槽的重要组成部分，弯道岔河水流相互交汇广泛存在于很多水力系统中，在交汇处水力特性受交汇口形状、交汇角度和雷诺数等因素影响会产生复杂的流体运动模式，不仅会影响弯道岔流流场的稳定还会影响弯道岔河附近过流建筑物的安全，因此，研究弯道岔河水力特性具有重要的理论和实际意义。目前国内外学者针对弯道岔河进行了大量研究：胥宗强［1］针对顺直明渠交汇水槽，采用大涡模型模拟了交汇区的湍流流场，并结合Werner壁面函数法求解近壁区流动，发现交汇口的三维几何特性与流场结构有较强的关联性；魏文礼［2］采用大涡模拟方法对交汇水流水力特性进行了模拟，结果表明：在整体上交汇角度越大，交汇口各特征横断面流速不均匀系数越大，即水流流速分布越不均匀。茅泽育［3］利用五孔测球对交汇口流场、速度大小、方向以及测点压强进行了测量，对明渠交汇口三维水力特性进行了试验研究。张挺［4］采用k-ω 紊流模型对90°明渠交汇口三维流场进行模拟，成功捕捉到了交汇口水面变化及二次流等主要水流特性，结果表明随流量比的增加支渠入口水流偏转角逐渐增加。周舟［5］得出同一流量比工况下，交汇角增大，交汇口附近水面变幅增大；同一交汇角度工况下，流量比增大，交汇口附近水面变幅减小的结论。Mosley M P［6］通过采用自然河工物理模型，分析研究了“Y”型汇流水域的水沙问题，认为干支流的交汇角以及水流速度比对交汇河段的水流结构以及河床地形发展情况具有重要的控制作用。N Rivière G［7］说明了在给定入口流量和出口条件下的某种形式的水位流量关系的情况下，如何使用得到的方程组计算任何类似交叉口的流量分布。冯镜洁［8］采用k-ε 双方程模型模拟流场，选用VOF 模型模拟自由面，依据物理实验条件对交汇式河流进行了三维数值模拟，研究表明在汇口下游主流右侧出现分离区，分离区的形状随着入汇角的减小而变得狭长，分离区的尺寸随着入汇角度和汇流比的增大而增大。M Leite Ribeiro［9］通过研究瑞士罗纳河上游汇合处的三维速度场、湍流等提出了水-形态-沉积过程的概念模型，并与现有的不同特征汇合流概念模型进行了比较。Hao Luo［10］提出了一种改进的一维非线性动力学模型，分析不同控制条件下汇流流体动力学和三维紊流结构的变化。赵振江［11］研究结果表明隔墩的布置可少量提升叶轮进口流速均匀度，改善进水流道两侧流速较低情况。周珊珊［12］得出无整流措施时进水池内出现不良流态；当布置了导流墩，可以很好地改善进水池内的不良流态从而进一步改善水泵的进水条件。向迁卿［13］采用试验方法研究了墩头为半圆形的中隔墩在不同水头下的流量系数，并与无中隔墩情况进行了对比分析，结果表明中隔墩对泄流能力的影响可用侧收缩系数反映。周杨［14］实验表明隔墩在侧向进水间整流具有一定效果，能改善水流流态。冯倜倜［15］实验表明多组偏斜导流墩可以改善某侧向进水泵站前池内存在的漩涡、偏流等不良流态。以上弯道岔河研究对象大多为人工河渠，但天然三岔河口复杂多变、无明显交汇角，往往需要就实际情况进行分析研究，且上述研究表明一字导流墩对水流具有一定的整流效果。为了研究一字导流墩对岔河流态的调整效果，本文以弯道岔河进流的铜城闸为研究对象，为了改善其复杂的进流条件，使用一字导流墩对其流态进行调整，以流速矢量和闸墩方向之间的夹角建立指标，从而对一字导流墩调整效果进行了评价，利用明渠面层数字粒子图像测速（DPIV）系统测得其流场参数，同时采用FLUENT 软件进行数值模拟，再利用Tecplot 进行后处理。得出不同位置一字导流墩整流措施下的进水流态再进行分析对比，为改善弯道岔河进流调整提供可借鉴的方案。

1 试验方法

1.1 物模试验

铜城闸共11 孔，每孔宽8 m，河道宽度在150～300 m 左右。模型总体布置见图1（a），为了保证模型水流在阻力平方区，模型有满足要求的水深，同时根据试验大厅场地以及试验主要目的，考虑采用1∶60比尺的正态模型。又因为本工程水流含沙量小，河床变化小，所以综合考虑模型采用定床正态河工模型。试验通过流量计及阀门控制模型进水流量，通过闸门和下游出水口叠梁式溢水板调节水位。当流量、水位稳定后采集流场数据。流量采用LDY-250S一体型电磁流量计和直角三角堰测量相互校核；水位采用WYG-Ⅲ型无线测控智能水位仪以及测压管、标尺互校测量；模型面层流态采用DPIV 技术，待水流稳定后在水面均匀地洒塑料悬浮粒子来观察面层流态，同时采用延时曝光的方式利用相机记录面层流场情况；底层流场采用红色化学试剂示踪法显示其流场，以便较好观察流态，具体物理模型试验见图1（b），流场测试见图1（c）。

图1 物模试验Fig.1 Model test

1.2 数模模拟

1.2.1 计算方程及网格划分

以连续方程和雷诺时均方程作为基本控制方程。连续性方程为：

雷诺方程为：

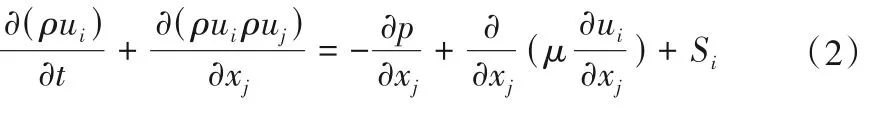
在Fluent求解器中采用标准k - ε湍流模型和SIMPLE算法作为软件计算的湍流模型和基本算法［16］。标准k - ε 模型的输运方程中的k方程为：

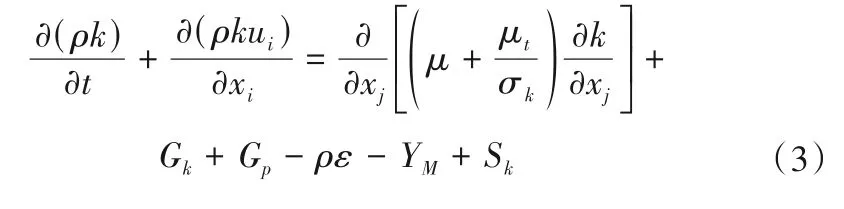
ε方程：

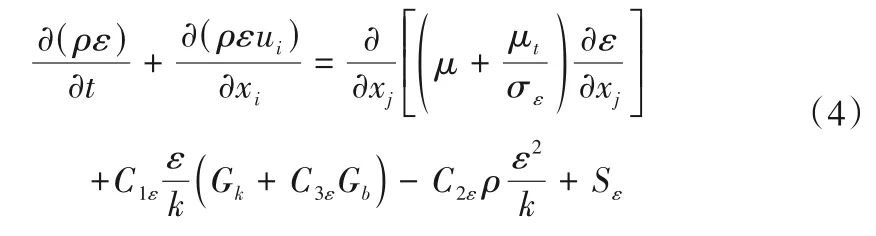
式中：k 为紊动能；ε 为紊动耗散率；ui为速度分量；xi为坐标分量；ρ 水的密度；μt为紊动黏度系数；Gk为由层流梯度产生的湍流动能；Gp为由浮力产生的湍流动能；YM为在可压缩湍流中，过渡扩散的波动；C1ε、C2ε、C3ε均为常量；Sk、Sε均为自定义。

采用UG12.0建立河道几何模型。非结构化网格进行划分，提取上游后河水位，结合物理模型对不同水位下后河进行模型建立以及网格划分，以弯道上游的进水断面为计算域的流速进口边界，弯道下游和下游岔河为计算域的自由出口边界，每个出口采用静压边界条件，压力值设为1 atm。水位变化不大，采用对称边界处理。除了进出口、自由水面，其余部分均为固体壁面。计算步数为1 000 步，收敛精度为10-6。本文以6 个不同水位进行观测确定弯道上游进口水位、流量，见表1，并对这6种工况流场进行模拟。

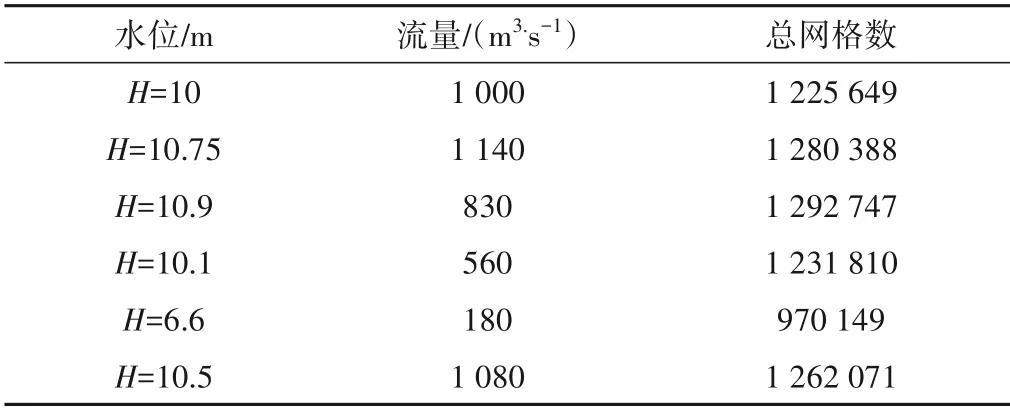
表1 不同网格划分下的水位和流量Tab.1 Water level and flow under different grids

1.2.2 方案设计

一字导流墩不同布置位置见图2（a），具体尺寸见图2（b），不同布置位置方案见表2。每个导流墩布置都顺水流方向。

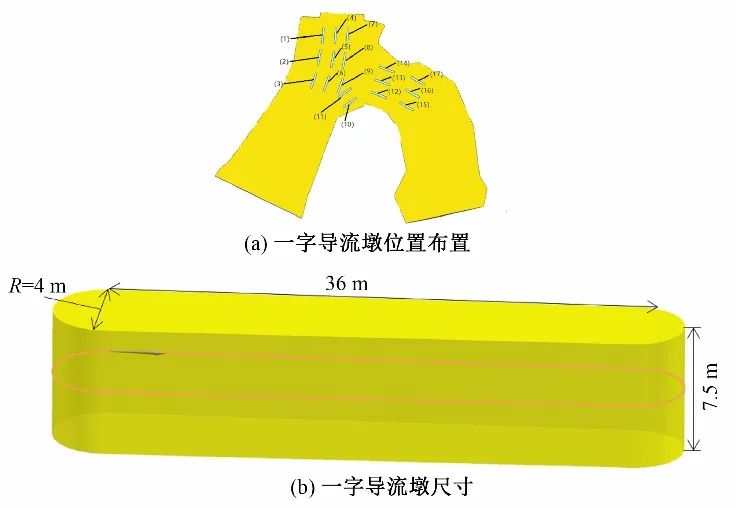
图2 一字导流墩位置布置和尺寸Fig.2 Layout position and size of linear shaped pier

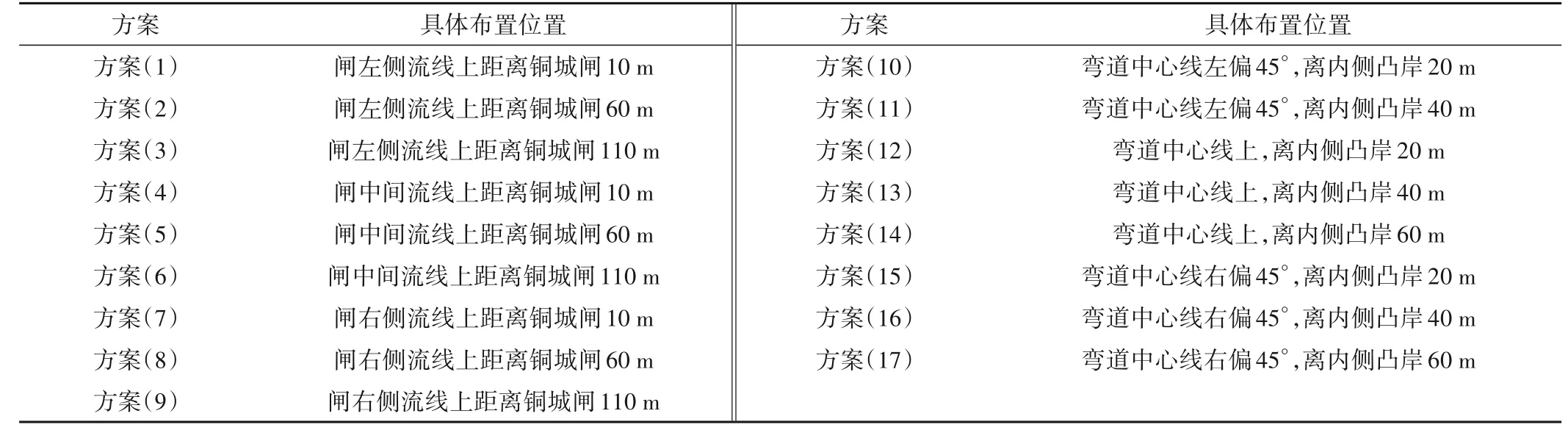
表2 一字导流墩不同布置位置方案Tab.2 Different layout positions for linear shaped pier

1.3 确定研究指标

为进一步量化和评价进闸流态，采用进闸水流与闸墩方向之间的最大夹角θmax、平均夹角、偏转系数θ1和θ2这4 个指标来评价进流流态平顺程度，其中；

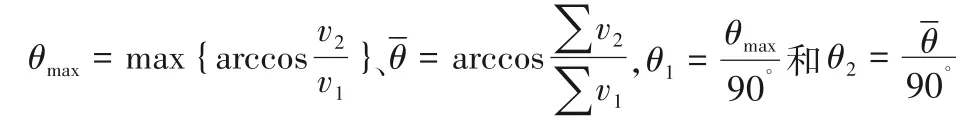
式中：v1为进闸流速矢量，m/s；v2为闸墩方向流速矢量，m/s。偏转系数θ1、θ2越接近于1，夹角越大，说明进流流态较差；反之偏转系数越接近于0，夹角越小，说明进流流态较好。

2 试验结果分析

2.1 原始工况分析

6 种不同工况：H=10、H=10.75、H=10.9、H=10.1、H=6.6、H=10.5 m 分别用序号a～f 表示。6 种不同工况在数学模型下，流速云图如图3 所示，从这6 种工况中选择流态最为复杂的情况作为研究对象，下文就以此最差流态作为基础再在不同位置加入一字导流墩，研究其对弯道岔河进流的影响。

由图3 中6 种不同原始工况流速云图可以看出，岔口的水流在经过弯道时受到离心力的作用会冲积下游凹岸和上游外侧堤岸，所以弯道下游流速偏大，而且进入铜城闸的部分水流由于惯性力冲击水闸闸墩以及翼墙的右前侧后不能及时调整会出现较大的偏角，从而造成闸前流态紊乱。工况b（即水位H=10.75 m）闸前有大范围的低速区，且大范围的低速区对于附近流速区梯度变化很大；工况b中闸前有大范围旋涡，同时闸两侧均出现明显的近岸旋涡，所以说明工况b进闸流态最差。

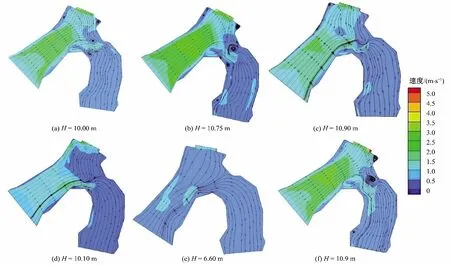
图3 6种原始工况流速云图Fig.3 Flow velocity cloud map of six original working conditions

为了更好地验证数学模型，在物理模型中调节H=10.75 m水位，观察此水位条件下面层流场流态，流速矢量图见图4（a），流速云图见图4（b），发现此水位面层流态很差。所以本文选取工况b组合（H=10.75 m，流量1 140 m3/s）做进一步研究。

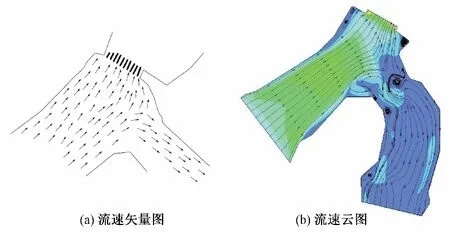
图4 工况b条件下流速矢量图和流速云图Fig.4 Flow velocity vector diagram and flow velocity cloud diagram under working condition b

2.2 一字导流墩整流分析

2.2.1 闸前设置一字导流墩

通过物理模型试验和数值模拟运算选出在闸前布置一字导流墩流态较好的4 个方案［方案（4）、（5）、（9）、（6）］，这4 个方案流速云图分别如图5所示。

由图5（a）可见，进入闸前的水流受一字导流墩影响，水流方向发生偏转，导致进入闸左侧的流速较大并使得闸右侧翼墙附近的旋涡更明显。由图5（b）可见，弯道凸岸有旋涡的形成，凹岸有大面积的低流速区，流速偏转进而影响闸前流态。由图5（c）可见，进闸水流与闸墩方向之间的夹角较大，水流受一字导流墩作用进入弯道，流线发生偏转，从而导致闸前水流不平顺，所以在闸右侧流线上设置一字导流墩不能很好地改善进流流态。图5（d）中的闸前流态较原始流态更加平顺，但是水流进入弯道后形成大范围低速旋涡，流线急剧偏转，虽然闸前流态改善明显但是弯道流态仍旧很差。从图5（a）、（b）可以看出，在此位置放置一字导流墩，闸前水流流线更加紊乱，而且进闸水流与闸墩方向之间的夹角较大。从图5（c）、（d）可以看出，在离闸较远位置放置一字导流墩对闸前流态可以很好的改善但是不能改善弯道流态。由图5 可得出，在闸前近距离放置一字导流墩会使进入闸左侧的流速较大，且随着一字导流墩逐渐远离闸，闸前的流态会越平顺，所以这四个方案，方案（6）较其他3个方案对闸前进流流态改善最明显。

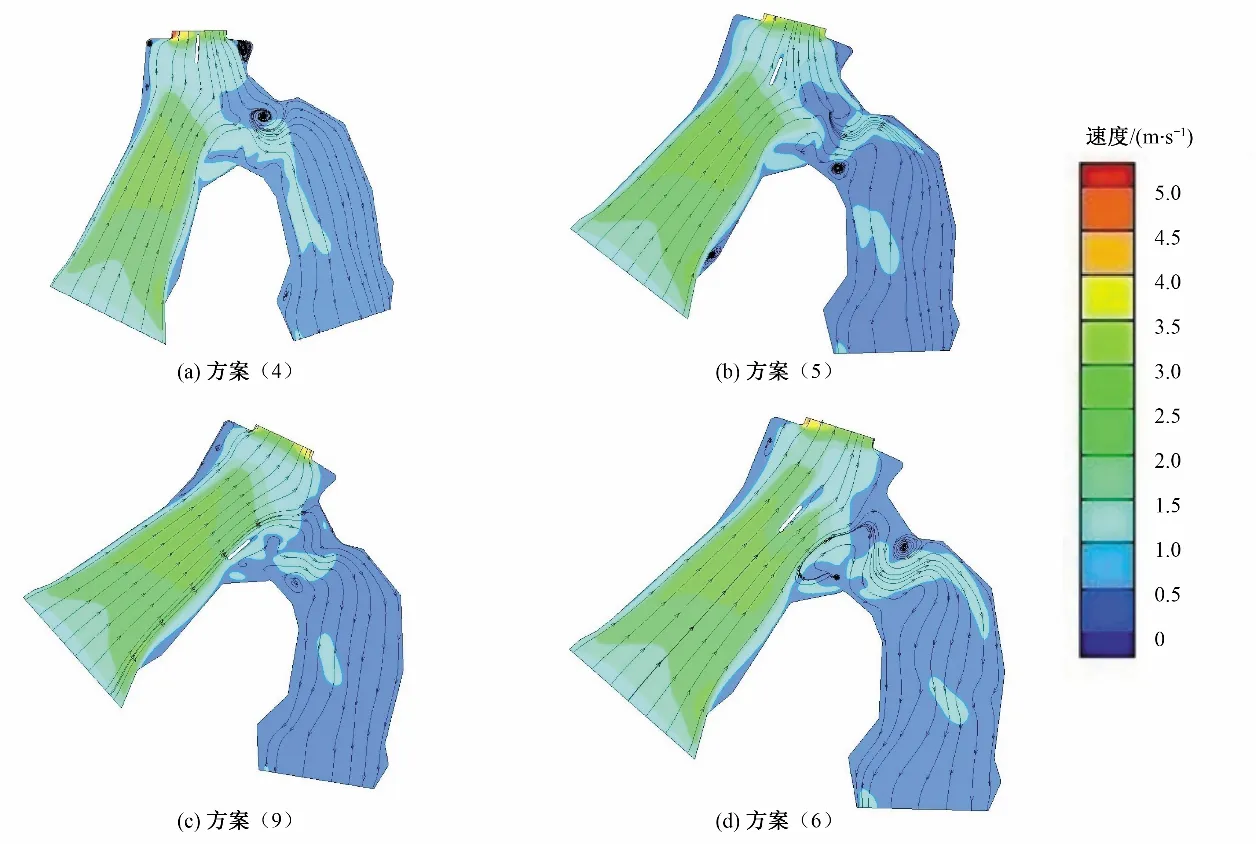
图5 闸前设置一字导流墩流速云图Fig.5 The flow velocity cloud map of the linear shaped pier set in front of the gate

2.2.2 弯道处设置一字导流墩

通过物理模型试验和数值模拟运算选出流态较好的4个方案［方案（15）、（13）、（14）、（12）］，这4个方案流速云图分别如图6所示。

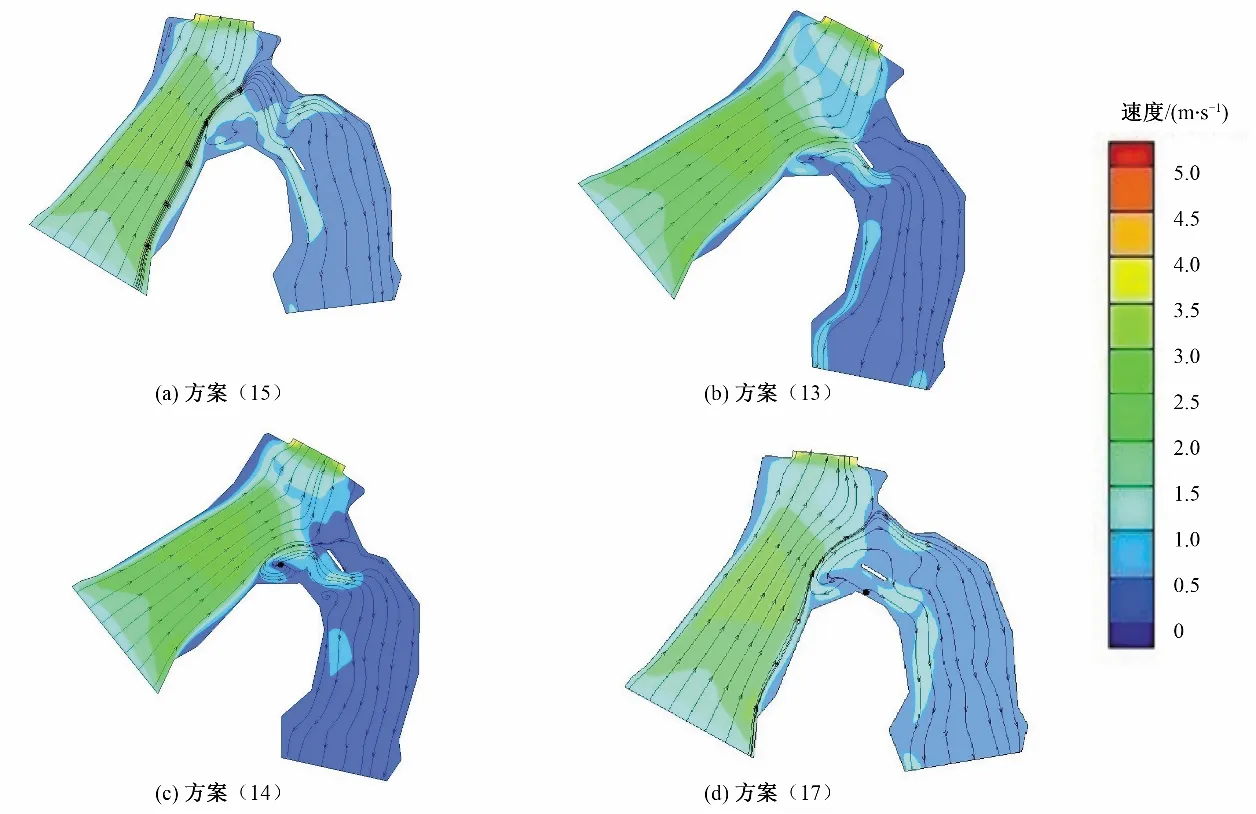
图6 弯道处设置一字导流墩流速云图Fig.6 The flow velocity cloud map of the linear shaped pier set at the bend

由图6（a）可见，一字导流墩设置在弯道下游，闸前流态没有受到调整，弯道内水流流线依旧杂乱，进流调整效果不理想。由图6（b）可见，在弯道中心线上设置一字导流墩，弯道内水流较平顺，但由于一字导流墩的整流作用，导致闸前水流受到弯道水流拉扯，闸前左右两侧进闸水流与闸墩方向之间的夹角较大而且闸前低速区较大，这对水闸造成了很大的不利影响，形成很大的安全隐患。由图6（c）可见，一字导流墩被设置靠近外侧凹岸，此时弯道内侧凸岸出现大范围涡旋及低流速区，进闸水流仍然受到弯道水流拉扯，闸前有多个低流速区而且闸前水流与闸墩方向之间的夹角较大，进流较乱。由图6（d）可见，一字导流墩被设置靠近内侧凸岸，弯道水流较为平顺，进闸水流与闸墩方向之间的夹角小部分偏大，大部分偏转角几乎为零，说明进流流态较平顺。虽然图6（d）闸前有低流速区，但比图6（b）、（c）缩小很多，而且进闸流速矢量与闸墩方向之间的夹角基本一致，所以这四个方案，方案（12）对闸前和弯道的综合调整效果最好。

对比图5（d）和图6（d）可得，图5（d）虽然闸前流态改善明显但是弯道流态仍旧很差，但是图6（d）对闸前和弯道处水流均有较好的调整效果，所以图6（d）较图5（d）调整效果好，即方案（12）效果最好。在其他工况（即H=10、H=10.9、H=10.1、H=6.6、H=10.5）下，通过数值模拟计算也是在弯道中心线上离内侧凸岸20 m 处设置一字导流墩对闸前水流和弯道岔口处水流调整效果最好。

2.2.3 调整前后流态分析

原始工况H=10.75 m流态云图和底层流场图，见图7（a）；在弯道中心线上离内侧凸岸20 m 处设置一字导流墩流速云图和底层流场图，见图7（b）。

图7 调整前后流态云图和底层流场图Fig.7 Before and after adjustment，the cloud map of the flow state and the underlying flow field map

对比调整前后流态云图和底层流场图可得，后者弯道水流较为平顺，进闸水流与闸墩方向之间的夹角也偏小，说明加入一字导流墩调整后进流流态较平顺；而且加入一字导流墩调整后，闸前低速区对于附近流速区梯度变化减小很多，说明有利缓解闸前有大范围旋涡的问题。所以在弯道中心线上离内侧凸岸20 m 处设置一字导流墩可以很好调整闸前和弯道岔口处水流流态，可用于工程实际。

2.2.4 进闸流速矢量与闸墩方向之间夹角的分析

进闸水流与闸墩方向之间的最大夹角θmax、平均夹角-θ、偏转系数θ1和θ2可以定量评价进闸流态平顺程度，其中平均夹角-θ 越小，说明整体水流流态更加平顺；偏转系数θ1、θ2越接近于1，则夹角越大，说明进流流态较差；反之偏转系数越接近于0，夹角越小，说明进流流态较好。通过计算分析上述闸前、弯道处8 种方案得出其最大夹角θmax、平均夹角-θ、偏转系数θ1和θ2，见表3。

表3 每个方案最大夹角、平均夹角和偏转系数Tab.3 Maximum Angle，average Angle and deflection coefficient of each scheme

通过对比发现，上述8 种方案的进闸水流与闸墩方向之间的最大夹角θmax分别减少了11.7%、29.4%、58.8%、11.7%、23.5%、64.7%、64.7%、41.2%；平均夹角-θ 除了方案4 增加27.5%，其他方案分别减少了17.5%、43.7%、8.7%、71.2%、62.5%、57.5%、18.7%；偏转系数θ1分别减少了5.5%、27.8%、5.5%、55.6%、11.1%、61.1%、61.1%、38.9%；偏转系数θ2除了方案4 增加28.4%，其他方案分别减少了17.0%、7.9%、43.2%、18.2%、62.5%、57.9%、71.6%；可见除了方案4，其他方案对进入闸的水流流态都有改善。由上表可见，一字导流墩距离闸越近最大夹角越大，而且平均夹角也越大，说明一字导流墩布置的位置距离闸越近，进入闸的水流流态越紊乱。在弯道中心线上布置一字导流墩最大夹角和平均夹角均小于在弯道中心线两侧布置一字导流墩。说明在弯道中心线布置一字导流墩比在两侧布置对进入闸的水流流态改善更好。方案12 偏转系数θ2低至0.025，最接近0，明显小于其他方案，说明方案12的进闸水流整体上是最平顺、对闸影响是最小的。虽然方案12最大夹角较大，但是平均夹角是最小的，说明方案12 进闸水流整体上更加平顺，结合上文的流速云图，方案12 进入三汊河的分流流速也有所减小，则对河道和河堤的冲刷也有所减小。综上，在弯道中心线上距离内侧凸岸20 m 处布置一字导流墩对闸前和弯道流态有明显的改善效果。

3 结 论

针对弯道岔河进流流态，本文采用铜城闸物理模型实验，并结合数值模拟来研究不同位置处设置一字导流墩对弯道岔河进流的影响，所得结果能较好地反映弯道岔河进流流态。本文以一字导流墩放置的不同位置为变量，对弯道岔河进流进行了详细的分析，所得主要结论如下：

（1）偏转系数可以被用来直接评价进流流态的优劣，偏转系数越接近于1，夹角越大，说明进流流态较差；反之偏转系数越接近于0，夹角越小，说明进流流态较好。

（2）闸前设置一字导流墩，随着其位置距离闸越远，闸前的流态会越平顺；其位置离闸越近，偏转系数越大。虽然对闸前流态有明显的改善，但是对弯道处流态改善效果较差。

（3）在弯道岔口处设置一字导流墩可以明显的改善弯道处的旋涡，在弯道中心线上离凸岸20 m 处布置一字导流墩，弯道和闸前流态均受到明显的改善。