基于跟驰模型的智能网联汽车混合交通流分析

赵辉

（兰州石化职业技术大学，甘肃 兰州 730060）

0 引 言

近年来，随着车辆拥堵、事故频发等交通问题的凸现，无人驾驶技术的研究变得尤为重要。美国汽车工程师学会将车辆自动驾驶等级划分为无自动驾驶（L0）、辅助驾驶（L1）、部分自动驾驶（L2）、有条件自动驾驶（L3）、高度自动驾驶（L4）及完全自动驾驶（L5）六类。随着无人驾驶技术的不断发展，智能网联车将逐渐普及。研究表明，预计2045年道路上L4 级别的智能网联汽车渗透率仅能达到24.8%。因此，未来很长一段时间内，人类驾驶车辆还会存在，道路上将普遍呈现由常规车（regularvehicle, RV）、CAV（connected and autonomous vehicles）组成的混合交通流。这两种类型的汽车将如何一起运行？本文讨论的混合交通流是解决这个问题的常用工具。为了更真实地描述交通动态，人们提出了跟驰模型，跟驰模型作为微观交通流模型已开发了几十年，并被广泛用于描述系统中单个汽车的移动行为，已成为智能交通领域的研究热点。W.X 等人利用跟驰模型研究了由RV 和CAV 组成的混合交通流的演变。Nakayama 等人提出了一种新的最优速度跟驰模型来研究智能网联车辆和人类驾驶车辆在跟驰过程中混合交通流的演变。M.BANDO等人创建了智能网联车辆跟驰过程中的优化速度函数。Ge 等人研究了智能网联汽车前车加速度反馈控制项模型的稳定性。Coifman基于检测器数据和交通流理论，估计路段行程时间重构了车辆的运行轨迹。Talebpour 等人利用跟驰模型，分析了智能网联车辆和人类驾驶车辆对交通流稳定性的影响。Ward通过Lyapunov 稳定性原理对混合交通流稳定性解析方法进行了推导，验证了智能网联车辆可实时获取前车的加速度数据，从而保证车辆的安全与稳定。

鉴于以上研究，本文基于跟驰模型，分析混合交通流稳定性的基本图。安排如下，在第1 节中，展示了人类驾驶汽车和智能网联汽车的动力学模型，先后给出了引理和定理。在第2 节中，分别在三种情况下进行了数值的仿真和模拟。在第3 节中，进行了总结。

1 动力学模型

1.1 模型假设

假设1：人类驾驶车辆和智能网联驾驶车辆的混合交通流在单车道上周期性边界条件下无超车行为。

假设2：两种类型车辆共计辆，且均匀分布在道路上。

假设3：道路中只有机动车辆，无其他不可抗力因素。

1.2 人类驾驶车辆模型

Bando的模型用于描述人类驾驶车辆，目前已被多人引用。它被制定为式（1）：

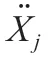
其中表示最大速度，l表示第辆车的长度。

利用线性稳定性理论分析车辆以常数运动的稳态均匀流动周期性边界条件下的车头和速度。方程中均匀稳态的解为式（3）：

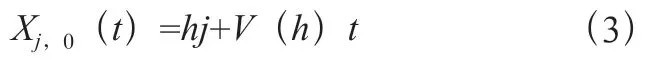
其中，=/，为相同的车头时距，为道路总长度，为车辆总数系统。根据经典线性系统稳定性理论，引理为：

引理1：如果满足式（4）中的下述条件：

则在最优速度模型的交通流中不会发生交通拥堵，否则会产生拥堵。

1.3 智能网联车辆模型

智能网联汽车安装有多个传感器，可以检测前后车头时距。基于Bando 的模型，智能网联汽车模型可以被描述为如式（5）：

其中是智能网联汽车上传感器的灵敏度。（ΔX（），ΔX（））是基于汽车上的前后传感器，可以描述为式（6）：

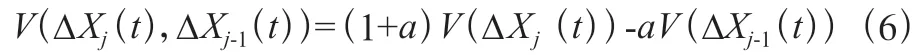
其中是一个常数。由于网联车内的电子传感器比驾驶员更敏感，因此灵敏度始终小于。

此模型的理念是，如果前车距大于后车距，那么汽车会具有更大的预期速度；如果前车距小于后车距，那么汽车将获得较小的预期速度；如果前车距等于后车距，那么汽车将获得预期的速度。

从上面的思路可以知道，由于因子不仅加强了车流的稳定性，而且也增强了安全性。它使智能网联汽车尽可能均匀地在道路上行驶。因此，参数模型中的被命名为“平滑因子”。

根据引理1：从上述新模型可以提出如式（7）的定理

定理1：如果满足以下条

则交通拥堵不会发生在智能网联驾驶汽车流中。否则，就会产生交通拥堵。

由引理1、定理1 及平滑因素，绘制出中性稳定线，如图1所示。图中，中性线以上的区域是非堵塞区域，中性线以下是堵塞区域。在=0 时，临界点是（17.59，1.913）。由上图可以得知，平滑因子越大意味着稳定区域越大。

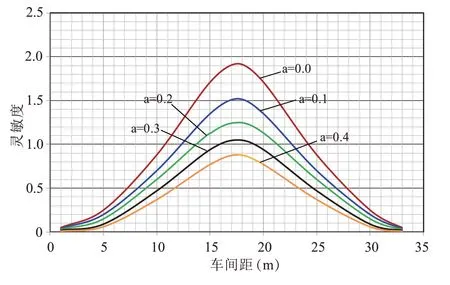
图1 不同平滑因子的中性稳定线

2 数值模拟

在周期性边界条件下，道路上的辆车没有超车的路程长度是米。汽车序列号是从第0 到第（-1）辆，第辆是该系统中的第一辆汽车。让[][] 和[][] 表示第辆车在时间的速度和位置。设定最佳速度函数为14.67 m/s，两种类型车辆的长度均相同，进行仿真。

2.1 灵敏度和平滑因子均不同的交通流模拟

本节将在两种情况下分别进行模拟，一为100%智能网联汽车交通流，二为50%智能网联汽车与50%人工驾驶汽车混合交通流。期间，交通流的变化密度可以通过两种方式实现。

首先，道路长度不变，汽车数量按固定值依次增加。表达式如式（8）：

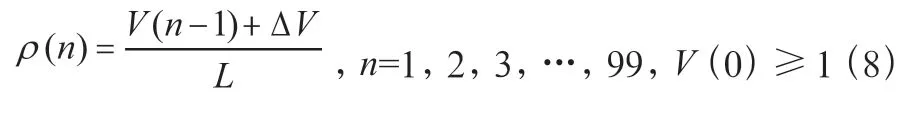
其中（）表示第次模拟的车辆数量，Δ是车辆的固定增加量。

其次，车号不变，道路长度按固定值依次递减。表达式如式（9）：

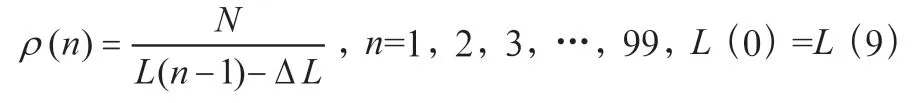
其中（）表示第次模拟的道路长度，Δ是固定减少的道路长度。交通流量的通量采用式（10）表示：

其中表示通量，表示流动密度，是一段时间内流动的平均速度。

2.1.1 100%智能网联汽车模拟

设定道路长度为=1 800 m，依次在系统中加入固定数量的智能网联汽车。根据式（10），每次增加5 辆智能网联汽车，共100 次。在以下两种情况下进行了模拟：不同的灵敏度=1.0、1.26、1.66、2.04 和平滑因子=0.0；仿真结果如图2所示。从图中可以观察到，基本图中存在临界点（ρ，Q）。当密度小于临界密度ρ时交通流的通量越大，对应的灵敏度也越大；当密度为大于临界密度ρ时，交通流的通量越大，对应的灵敏度越小。同理，模拟仿真变化的平滑因子=0.1、0.2、0.3、0.4 和灵敏度=1.0，可以得到类似的结论：平滑因子对交通流量有相同的影响，即在临界密度ρ之前，平滑系数越大，交通流量越大；在临界密度ρ之后，交通流量的变化呈相反趋势。

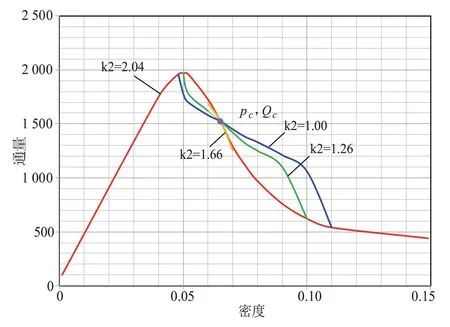
图2 不同灵敏度下智能网联汽车流动基本图

2.1.2 50%智能网联汽车与50%人工驾驶汽车模拟

此数值模拟以检测混合交通流中灵敏度和平滑因子的影响。当平滑因子不变=0.0，灵敏度取值分别为=1.0、1.26、1.66、2.04 时，仿真结果如图3所示。可以看出，灵敏度越大，在临界密度之前获得较大的交通流量，在临界点之后呈现相反的变化趋势。同理，当灵敏度不变=1.0，平滑因子取值分别为=0.1、0.2、0.3、0.4 时，可以得到类似的结论，即平滑因子越大，在临界密度之前获得较大的交通流量，在临界点之后呈现相反的变化趋势。

图3 不同灵敏度下的混合交通流的基本图

从以上模拟可以得出结论，无论是智能网联车流还是人类驾驶车辆与CAV 的混合交通流，通量在一定的密度范围内受灵敏度和平滑因素的影响。且对比图2和图3，可以看出，图3的密度变化范围明显大于图2，即混合交通流的稳定性弱于智能网联汽车流的稳定性。

2.2 智能网联车流稳定性模拟

2.2.1 不同灵敏度下交通流的稳定性

此模拟中，道路长度为1 800 m，智能网联汽车的数量为100 辆，灵敏度取以下值：=0.83、1.26、1.66、2.04，不考虑平滑因素。仿真结果如图4所示，图（a）和图（b）分别对应于=0.83，=0 和=0.24，=0，图中的模式展示了在时间=19 000 s 时智能网联汽车的前进曲线，可以看出，随着灵敏度的逐渐增大，智能网联驾驶车流的稳定性随之加强。因此可以得出：智能网联汽车流的稳定性可以通过以下方式增强：更大的灵敏度。

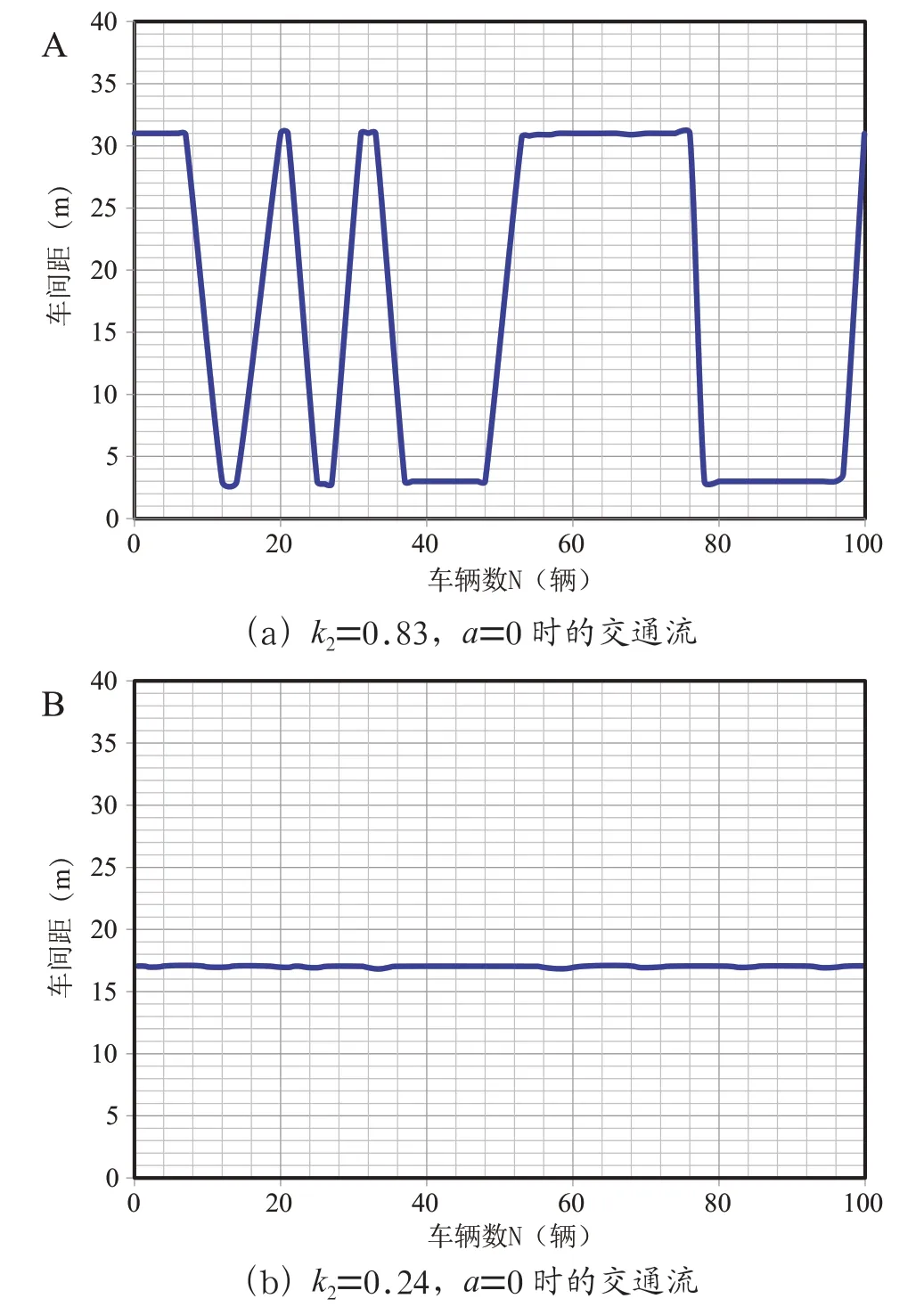
图4 不同灵敏度下智能网联车交通流的时距图

2.2.2 不同平滑因子下交通流的稳定性

此模拟中，灵敏度取为=1.0，平滑因子取为=0.1、0.2、0.3、0.4。采用与2.2.1 相同方法，仿真出具有不同平滑因子的智能网联汽车在=19 000 s 时的车头时距曲线。可以得出相似的结论：智能网联驾驶车流的稳定性随着平滑因子的增加而增强。即智能网联车流的稳定性还可以通过另一种方式得到增强：更大的平滑因子。

2.3 混合交通流稳定性模拟

2.3.1 不同灵敏度下混合交通流的稳定性

此模拟中，混合交通车流总数为100，道路长度为1 800 m。智能网联汽车中灵敏度取值依次增大，分别为：=0.83、1.26、1.66、2.04，平滑因子取0，不考虑CAV的后车距。如图5展示了在=19 000 s 时不同灵敏度的混合交通流，图5（a）和图5（b）分别对应于（=0.83，=0.83，=0）和（=0.83，=2.04，=0）。从图中可以观察到，车头时距振荡的幅度随着灵敏度的提高而变小。这意味着混合车流的稳定性随着灵敏度的增加而加强。

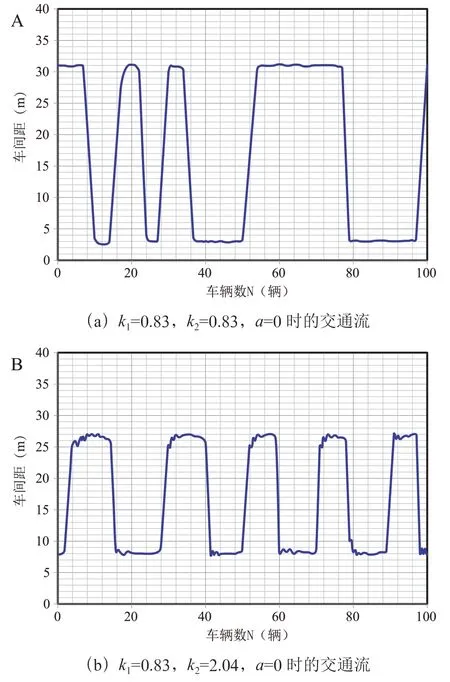
图5 不同灵敏度下混合交通流的时距图

2.3.2 不同平滑因子下混合交通流的稳定性

此模拟检验了不同平滑因子=0.1、0.2、0.3、0.4 对混合交通流稳定性的影响。采用与2.3.1 相同方法，仿真出具有不同平滑因子的智能网联汽车=19 000 s 时的车头时距曲线。智能网联驾驶汽车的灵敏度取值为=2.5。可以得出相似的结论：车头时距振荡的幅度随着平滑因子的增大而变小，即随着平滑因子的增加，混合交通流的稳定性得到了加强。

3 结 论

本文分析研究了人类驾驶汽车和智能网联驾驶汽车混合的交通流。首先提出了一种具有灵敏度和平滑因子可调的智能网联驾驶汽车数学模型，并且基于定理进行了稳定性分析。得出在一定范围内，灵敏度和平滑因子可以影响车流的稳定性。

建立了三种不同车流的结构模型，通过模拟仿真，得出结论：（1）在一定边界条件下，100%智能网联汽车交通流的稳定性强于混合交通流的稳定性。（2）通量在一定的密度范围内受灵敏度和平滑因素的影响，随着灵敏度和平滑因子的增大，智能网联驾驶车流及混合交通流的稳定性均随之加强。即智能网联车流和混合交通流的稳定性可以通过以下两种方式增强：更大的灵敏度和更大的平滑因子。