汽车起重机泵阀复合系统高性能控制研究*
和进军,贾鹏硕,唐琛淇,李 凯,谢 帅,艾 超
(1.三一汽车起重机械有限公司,长沙 410600;2.燕山大学机械工程学院,河北秦皇岛 066004)
0 引言
汽车起重机具备机动性能强、承载能力大、适用范围广等多方面的突出优势,在建筑工地、桥梁交通、港口搭建等多方向工程领域中实现了广泛应用[1]。目前起重机控制系统普遍采用传统的负载敏感液压系统,但负载敏感系统需要预设一定的压力裕度实现泵口压力闭环控制,导致这部分压力均损失在压力补偿阀和换向主阀上,使得系统能耗较大[2]。泵阀复合控制系统是通过永磁同步电机和比例阀的协同控制实现起重机变幅伸缩机构的单独和复合动作,节能效果好。但由于系统中存在永磁同步电机转速波动、液压泵流量非线性等因素,使得变幅伸缩机构的控制精度不高,动态性能受限[3-4]。
李锐等[5]提出了改进径向基函数(RBF)神经网络PID控制方法,设计了负载敏感平衡阀,经过实验证明,能够有效改善系统控制精度。Sakaino和Tsuji[6]提出基于反馈调节器和扰动观测器,设计控制器以消除摩擦力干扰,增强了液压系统的鲁棒性。Ren等[7]利用系统识别提出了低带宽线性控制器,获得良好的鲁棒性,可以降低噪声,消除未建模的高频动力学影响。韩小霞等[8]针对泵控系统控制精度低的问题,对泵控系统流量死区数学模型进行研究,提出动态逆补偿的方法,改善了控制性能。付永领等[9]针对泵控系统参数不确定性扰动的问题,通过对系统内存在的摩擦特性的分析,设计新型的自适应模糊控制算法,使得跟踪速度得到提高。Helian B等[10]通过实际拟合提出了非线性泵流速图,将所需泵流量的适当非线性补偿将其用于控制器设计,实现了高性能控制。
本文以起重机变幅伸缩机构为研究对象,对电机泵组输出流量控制进行研究。详细介绍了泵阀复合控制系统的工作原理,建立流量控制数学模型,针对系统中存在的电机转速波动、泵输出流量非线性等影响因素,将模糊算法动态响应好、鲁棒性强的特性和传统PID稳态精度高、稳定可靠的优点进行整合,提出模糊PID线性复合控制器,最后通过与传统PID控制的仿真对比验证了该方法的有效性,提高了系统流量控制性能。
1 泵阀复合控制系统
汽车起重机变幅伸缩泵阀复合控制系统液压原理如图1所示。

图1 泵阀复合控制系统液压原理Fig.1 Hydraulic principle of pump and valve compound control system
系统将变幅伸缩电手柄信号反馈到控制器中,控制器进而判断变幅伸缩机构处于单动还是复动状态。当系统处于单独动作时,控制器根据手柄的开度大小给定电机相对应的转速值,通过泵口流量传感器信号反馈,实现对流量的控制,比例主阀开度最大,仅实现换向。当系统处于复合动作时,控制器计算变幅伸缩机构所需的总流量,进而给定电机转速,使得液压泵输出基础流量,变幅伸缩机构各自所需的流量再由比例主阀进行调节,实现泵阀复合协同控制。
在传统的负载敏感系统中,输入到变幅伸缩机构的流量仅由比例主阀调节,非线性影响因素少。而泵阀复合控制系统在阀控系统的基础上,又加上泵控系统,电机转速波动、液压泵流量非线性等因素严重影响了系统的控制性能。所以本研究主要针对泵控系统的控制理论进行研究,改善流量控制的动态响应和控制精度。
2 泵阀复合控制系统电机泵组数学模型
2.1 永磁同步电机
永磁同步电机负责将控制输入电压转化成电机输出转速,电机输出转速与输入电压信号之间的关系为:

式中:Uq为电机q轴电压,V;Rs为电机绕组阻值,Ω;L q为q轴电感,H;iq为q轴电流,A;ωm为电机输出转速,rad/s;Ke为永磁体反电动势系数,V/(rad·s-1);Te为电机扭矩,N·m;Kt为电机扭矩系数,N·m/A;TL为液压泵产生的反扭矩,N·m;Dp为液压泵排量,m3/rad;pL为液压泵两腔压差,pL=pA-pB,Pa;Jm为电机泵转动惯量,kg·m2;Bm为电机泵运动副产生的与ωm相关的摩擦因数。
整理式(1)得:
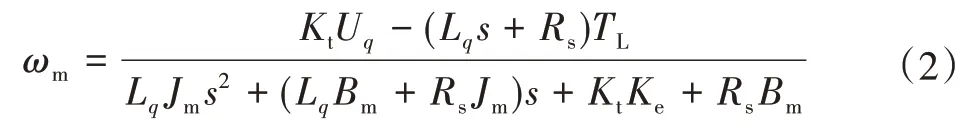
2.2 液压泵
考虑油液压缩与内外泄漏等因素分析定量泵流量分布特性,如图2所示。

图2 液压泵流量分布Fig.2 Flow distribution of hydraulic pump
假定液压泵的泵容积排量为常数,从泵到被控液压缸的两腔负载容积流量可表示为:

式中:qA为系统流量,m3/s;qB为泵吸入的油箱油液流量,m3/s;Cip为泵的内泄漏系数,(m3·s-1)/Pa;Cep为泵的外泄漏系数,(m3·s-1)/Pa;pA为系统负载压力,Pa;pB为标准大气压力,Pa。
联立式(2)、式(3)可以得到泵阀复合控制系统由输入电压Uq到输出流量qA的数学模型。
3 模糊PID控制器设计
常规PID控制具有较高的精度,良好的稳定性,但面对系统多种非线性干扰,适应性较差;模糊控制动态性能较好,适应能力强,却无法获得较高的稳态精度,可能会发生震荡。所以研究将两种方法进行组合,形成模糊PID线性复合控制结构,如图3所示。
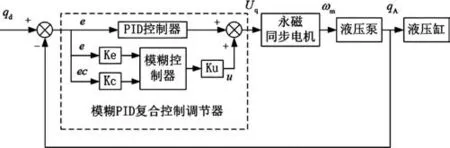
图3 模糊-PID复合控制结构Fig.3 Block diagram of fuzzy-PID compound control structure
(1)模糊控制器结构
采用二输入一输出构架。输出量为控制量u,输入量为系统给定流量qd和泵出口反馈流量qA的偏差e和偏差变化率ec,将复合控制器输出传输给电机,进而控制系统流量。
(2)输入和输出变量论域
设定ec和u的模糊集合为:
{NB,NM,NS,O,PS,PM,PB}
设定偏差e的模糊集合为:
{NB,NM,NS,NO,PO,PS,PM,PB}
为了得到更高的精度需求,将O分成了NO、PO两个部分。
(3)模糊制规则表和隶属函数
模糊控制规则的建立是模糊推理法能成功应用的保证,模糊推理符合一般推理方法的逻辑。模糊控制规则如表1所示。可以通过模糊量赋值得到e、ec以及u的隶属函数,再利用MATLAB模糊工程箱结合隶属函数得到输出曲面图,如图4~7所示。

表1 模糊控制规则Tab.1 Fuzzy control rule list
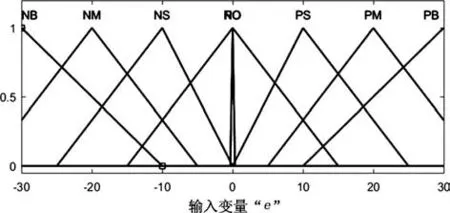
图4 模糊控制对于偏差为e的隶属函数图像Fig.4 Fuzzy control for the deviation of e membership function image

图5 模糊控制对于偏差为ec的隶属函数图像Fig.5 Fuzzy control for the deviation of ec membership function image

图6 模糊控制对于控制量为u的隶属函数图像Fig.6 Fuzzy control for the control quantity u membership function image

图7 模糊控制综合输出曲面Fig.7 Fuzzy control integrated output surface diagram
4 系统仿真分析
4.1 仿真模型建立
利用Simulink构成模糊PID线性复合控制系统和传统PID控制系统仿真模型,如图8~9所示。

图8 PID控制仿真模型Fig.8 PID control simulation model diagram
在Simulink仿真过程中,模型参数设置是十分重要的一部分,整体参数赋值结合元件技术样本,得到其系统参数如表2所示。

表2 仿真模型参数Tab.2 Simulation model parameter Tab
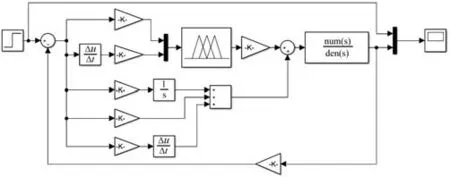
图9 模糊PID复合控制仿真模型Fig.9 Simulation model diagram of fuzzyPID compound control
利用Simulink模糊控制箱,运用试凑法对模糊PID控制器与传统PID控制器中的参数进行调整,能够得到控制过程中最佳的各个参数的值。
模糊PID复合控制器的偏差因子KE、偏差变化因子KEC以及控制量因子KU分别是0.45、0.003、50,其中PID参数为:Kp0=900,Ki0=2,Kd0=1;传统PID控制器参数为:Kp=800,Ki=2,Kd=1。
4.2 60 L/min阶跃仿真分析
给定泵阀复合控制系统一个60 L/min的阶跃信号,得到传统PID控制系统的阶跃响应及其偏差曲线,如图10~11所示。

图10 PID控制阶跃响应曲线Fig.10 PID control step response curve
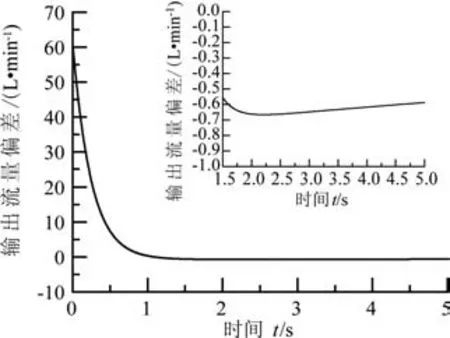
图11 PID控制阶跃响应偏差曲线Fig.11 PID control step response deviation curve
模糊PID线性复合控制系统的阶跃响应及偏差曲线如图12~13所示。

图12 模糊-PID线性复合控制阶跃响应曲线Fig.12 Step response curve of fuzzy-PID linear compound control

图13 模糊-PID线性复合控制阶跃响应偏差曲线Fig.13 Step response deviation curve of fuzzy-PID linear compound control
为了分析方便,将实际系统流量输出曲线和期望流量曲线放到同一界面显示,通过60 L/min流量阶跃响应曲线进行分析,可以得出以下结论:传统的PID控制器动态响应速度较慢,在2 s后系统才逐渐趋于稳定,而且稳态误差比较大,达到了0.67 L/min。而模糊PID线性复合控制器在1.5 s后系统便趋于到达稳态,且输出流量精度可以控制到0.34 L/min以内。
4.3 120 L/min阶跃仿真分析
给定泵阀复合控制系统一个120 L/min的阶跃信号,传统PID控制系统的阶跃响应及偏差曲线如图14~15所示。
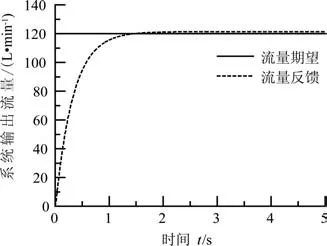
图14 PID控制阶跃响应曲线Fig.14 PID control step response curve
模糊PID线性复合控制系统的阶跃响应及偏差曲线如图16~17所示。

图16 模糊-PID线性复合控制阶跃响应曲线Fig.16 Step response curve of fuzzy-PID linear compound control
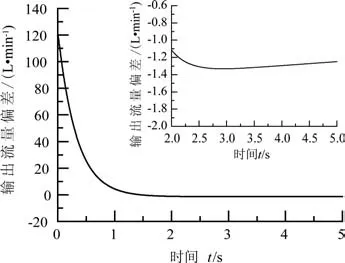
图15 PID控制阶跃响应偏差曲线Fig.15 PID control step response deviation curve

图17 模糊-PID线性复合控制阶跃响应偏差曲线Fig.17 Step response deviation curve of fuzzy-PID linear compound control
对流量控制系统在PID控制器、模糊PID线性复合控制器下的120 L/min流量阶跃响应曲线进行分析,可以得出以下结论:传统的PID控制器动态响应速度较慢,在2.5 s后系统才逐渐趋于稳定,而且稳态误差比较大,达到了1.33 L/min。而模糊PID线性复合控制器在1.8 s后系统便趋于到达稳态,且输出流量精度可以控制到0.68 L/min以内。
4.4 180 L/min阶跃仿真分析
当给定泵阀复合控制系统一个180 L/min的阶跃信号时,传统PID控制系统的阶跃响应曲线如图18所示,阶跃响应偏差曲线如图19所示。

图18 PID控制阶跃响应曲线Fig.18 PID control step response curve

图19 PID控制阶跃响应偏差曲线Fig.19 PID control step response deviation curve
模糊PID线性复合控制系统的阶跃响应及偏差曲线如图20~21所示。

图20 模糊-PID线性复合控制阶跃响应曲线Fig.20 Step response curve of fuzzy-PID linear compound control

图21 模糊-PID线性复合控制阶跃响应偏差曲线Fig.21 Step response deviation curve of fuzzy-PID linear compound control
对流量控制系统在PID控制器、模糊PID线性复合控制器下的180 L/min流量阶跃响应曲线进行分析,可以得出以下结论:传统的PID控制器动态响应速度较慢,在3.5 s后系统才逐渐趋于稳定,而且稳态误差比较大,达到了1.98 L/min。而模糊PID线性复合控制器在2.5 s后系统便趋于到达稳态,且输出流量精度可以控制到1.02 L/min以内。
综合以上可以判断,相比传统PID控制器,系统在模糊PID线性复合控制器下的流量输出不仅动态响应快,且具有更好的稳态精度。
5 结束语
本文以起重机变幅伸缩机构为研究对象,针对泵阀复合控制系统因受到永磁同步电机转速波动、液压泵流量非线性等因素影响而出现的精度不高,动态性能受限问题进行研究,得到结论如下。
(1)搭建泵阀复合控制系统电机泵组非线性数学模型,设计一种模糊PID线性复合控制器并利用模糊工程箱在Simulink中完成控制器仿真模型搭建。
(2)分别对PID控制系统和模糊PID线性复合控制系统输入流量阶跃信号进行仿真,基于仿真结果可知,对比PID控制系统,本研究提出的模糊PID线性复合控制器使得泵阀复合控制系统动态响应时间缩短0.5~1 s,流量稳态精度提升50%,有效改善了泵阀复合控制系统的控制性能。

