求解固体力学问题的强-弱耦合形式单元微分法1)
胡 凯 高效伟 徐兵兵
(大连理工大学航空航天学院,工业装备结构分析国家重点实验室,辽宁大连 116024)
引言
在计算力学中,常用的数值算法基本上可以分为以下几类:基于单元的网格类算法[1-2]、基于散点的无网格法[3-5]、基于边界积分方程的边界元法[6-7]、以及一些其他数值算法,例如比例边界有限元法[8]、等几何法[9]、有限块法[10]等.这些算法又基本上可以分为两类:一种是基于变分法或者加权余量法的弱形式算法,一种是基于配点法的强形式算法.基于加权余量法的弱形式算法通常有较高精度和更好的稳定性,如以上提到的广泛使用的有限元法FEM.基于配点法的强形式算法具有更简单的构造形式以及更快的计算效率,如无网格法中的有限点法[11]、径向基点插值法[12-15]、自由单元法[16-17]等.基于分域算法的有限块法以及等几何配点法[18-20]也属于强形式算法.但是配点法,特别是基于散点的无网格配点法的精度以及稳定性较差.
为了克服以上配点法的缺点,基于单元的强形式算法应运而生,如强形式有限元法[21-22]、节点梯度光滑有限元配点法[23]等.近年来,高效伟等[24-25]提出了一种求解二维及三维问题的新型强形式有限单元法——单元微分法EDM,并导出了二维及三维问题中形函数关于全局坐标的一阶及二阶偏导数的显式表达式.目前,单元微分法已经用于求解静力学问题、热学问题[26-27]、动力学问题[28]、压电问题[29]等多种单场及耦合场问题.与传统配点法不同,单元微分法使用单元进行插值离散,因此具有更高的稳定性.与有限元法相比,由于不需要数值积分,因此具有更高的效率.当使用高阶拉格朗日插值时,该算法具有较高的精度.但由于单元面中节点使用了应力平衡方程,对于一些模型中存在应力奇异的问题,如断裂力学问题、V 型切口问题、间断边界问题等,单元微分法往往得到精度较差的结果.
为了解决此类问题,郑永彤[30]等开发了弱形式的单元微分法,即对每个单元的内部点构造加权余量弱形式,并针对间断边界问题进行分析,得到了更精确的结果.但是由于每个单元都用到了数值积分,会带来计算效率的降低.并且由于没有改变界面点使用通量平衡这一方程,该算法在解决应力集中问题时仍存在一定问题.
为了解决以上问题,在本文中提出了将单元微分法与传统有限元法相结合的耦合式算法.即对于模型的大部分,采用单元微分法,而对于模型中存在应力集中的部分以及采用强形式EDM 计算不准的区域,采用有限元法.通过这样的处理,可以在保证计算效率的同时,提高算法的计算精度.本文将详细描述单元微分法的基本原理,强-弱耦合算法的构造,以及该耦合算法在二维及三维力学问题中的应用,并对该耦合算法的精度,效率进行比较.
目前,求解固体力学问题中还未使用到强-弱耦合形式的单元微分法进行计算,因此对于该算法的研究非常有必要.
1 弹性力学基本方程
考虑一个处于平衡状态的弹性体 Ω∈Rd,其计算域的边界为 ∂Ω=Γ=Γu∪Γt,其中 Γu为位移边界,Γt为通量边界,d为问题的维度.则弹性力学所满足的控制微分方程如下:给定fi:Ω→Rd,gi:Γu→Rd,ti:Γt→Rd,寻找ui:→Rd,使得

其中,σij为柯西应力张量,fi为体积力,gi为给定位移,ti为模型边界面力矢量,nj为 Ω 的外法线.在本文中,公式的重复指标代表求和.
应力张量和应变张量的关系可由以下广义胡克定律给出

其中,εkl为应变张量,Di jkl为四阶弹性本构张量,其表达式分別为

式中,uk为位移矢量,μ 为剪切模量,ν 为泊松比.将式(3)代入式(2),并利用本构张量的对称性,将所得结果代入式(1)中,可得均质问题的弹性力学控制方程

及其面力边界条件
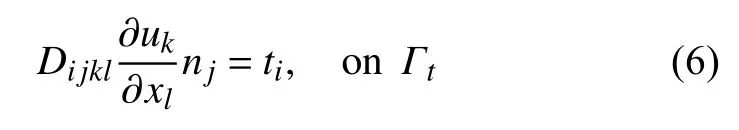
2 单元微分法的基本原理
为了通过数值方法求解以式(5)及式(6)为控制方程的弹性力学问题,第一步需要对计算域进行分片离散.和传统基于网格的算法类似,计算域 Ω 被离散为一系列互不重叠的四边形或六面体有限单元



此外,未知变量f的p阶导数可以表示为以下形式
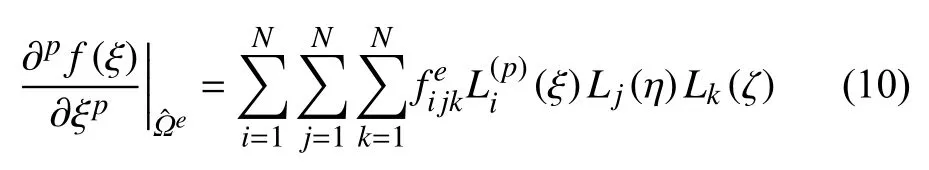

其中,Nα称之为单元的形函数,m为单元 Ωe内的节点数量.在本文中,为了减小矩阵带宽及计算量,式(8)~式(10)中变量N通常取3.
接下来的问题是要处理不规则计算域的问题.对于几乎所有的物理问题,其计算域往往并不是规则的.因此,需要用到坐标转换技术,即建立函数对整体坐标的导数与函数对参数坐标的导数之间的关系.考虑计算域 Ωe内的某连续函数f,其一阶导数可通过以下方式获得

对于强形式算法,需要用到函数对全局坐标的二阶导数.为了获得单元的二阶导数,通过对式(12)进行再次微分,可得函数对全局坐标的二阶导数的显式表达式为

其中Jik为坐标变换的雅克比矩阵,其逆矩阵可通过下式计算

此外,式(13)中雅克比的逆矩阵关于局部坐标的导数为
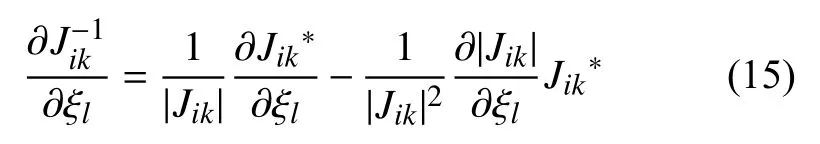
将式(14)及式(15)代入式(12)及式(13)中,并考虑式(11),可得变量关于全局坐标的一阶导数及二阶导数为

从式(16)及式(17)中可以看出,通过计算形函数关于全局坐标的一阶及二阶导数,可得函数f关于全局坐标的导数.以上变量关于全局坐标的一阶导数及二阶导数在单元微分法及有限元法均有相关应用.针对二阶导数计算式(17),其相关具体每一项的展开式可见EDM 的文献[24-25].
3 强-弱耦合形式算法
现有的数值算法可以分为两大类:基于强形式的配点类算法和基于弱形式的伽辽金类算法.单元微分法是一种强形式算法.和配点类无网格法不同的是,单元微分法基于类似有限元法中的单元,而非散点,因此算法的稳定性要高于传统的无网格法.由于不需要进行积分,其易用性、效率等方面都优于传统有限元法.但是作为一种强形式算法,针对具体问题要达到较高的计算精度,往往需要更多的网格,尤其是针对具有应力集中的问题.为了解决以上问题,可以尝试将单元微分法和有限元法进行耦合计算,即在利用单元微分法优点的前提下,提高其在求解具体问题时的能力.如图1 所示为一个具有切口的二维模型的网格图,其在切口附近的单元使用有限元法,其他部分的单元采用单元微分法.

图1 单元微分法和有限元法耦合形式的模型离散方案Fig.1 Model discretization scheme in coupling form of element differential method and finite element method
3.1 单元微分法
作为一种强形式的有限元法,单元微分法和其他强形式的无网格法的基本思想类似,通过将形函数关于全局坐标的一阶导数及二阶导数直接代入到控制方程及边界条件中构造系统方程.和强形式无网格法不同的是,该算法基于网格而非散点,因此稳定性更好.
如图2 中所示,在单元微分法中,将模型中的点分为两类:处于单元内部的点,称之为内部点;处于单元边界的点,称之为边界点.对于内部点来说,其满足具有二阶导数形式的控制方程(式(5)),对于单元边界点,其满足具有一阶导数形式的面力平衡方程(式(6)).
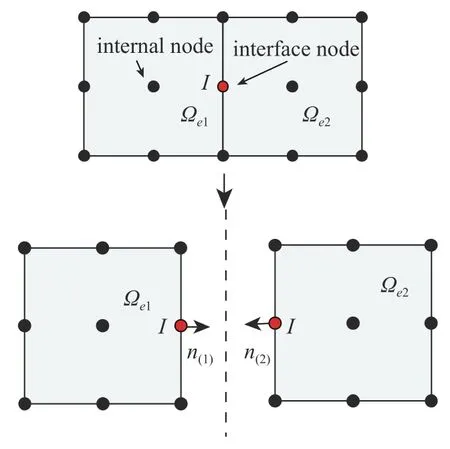
图2 单元内部点及单元边界点Fig.2 Element internal nodes and element interface nodes
对于内部点,将函数关于全局坐标二阶导数的微分关系式(17)代入式(5)中,可得以下方程

在上式中,出现了形函数对全局坐标的二阶导数.这部分公式的推导见第二章.
对于单元边界点I,其通常与NI个单元相连.对于任意一个相连的单元e,单元边界点I与单元e的SeI个单元面相关.根据所处位置不同,单元边界点可分为两类:模型内部点和模型边界点.对于模型内部的单元界面点,其满足通量平衡方程,即
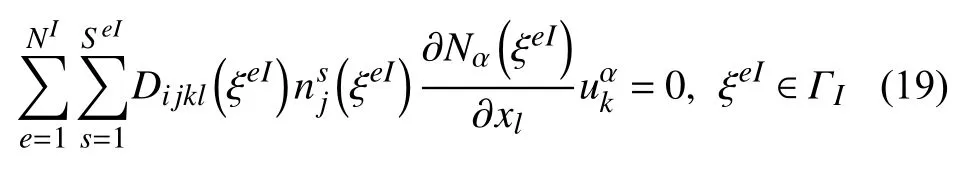
对于模型边界节点,其满足的方程和模型内部界面点方程(式(19))类似,不同的是方程右端项为指定面力,即对于模型边界点,有

对于一个EDM 单元,可依次根据式(18)~式(20)对单元的节点进行方程组集,形成单元系数矩阵,并可组装成整体刚度矩阵.
3.2 有限单元法
有限元法是一种弱形式算法.在本文提到的强弱耦合形式的算法中,将采用伽辽金有限元法与单元微分法相结合的形式求解问题.在本文中,将使用加权余量法简要推导相关方程.
对于单元中的每个配置点,权函数w取为计算点所在单元 Ωe的插值形函数N*.考虑弹性力学控制方程(5),可得到以下积分形式

对于上式,考虑分部积分,采用高斯散度定理,并考虑面力边界条件(6)和形函数离散式(11),可得
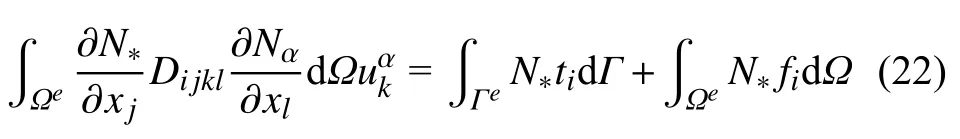
其中 Γe为单元 Ωe的边界.从上式可以看出,伽辽金有限元法中只出现了形函数对全局坐标的一阶导数,可采用第2 节中推导的公式直接计算.对单元中每个点进行计算,可得有限元的单元刚度阵.
3.3 耦合形式算法
从上两节中可以看出,单元微分法在计算形成系统方程组的过程中,采用与无网格法中的配点形式相似的方法,不需要对控制方程进行积分变换,但需要计算单元中函数对整体坐标的二阶偏导数.而对于有限元法,通过分部积分,只需要计算单元中函数对整体坐标的一阶偏导数.并且由于使用积分,计算精度较单元微分法高,但是FEM 计算需要用到高斯数值积分,计算量较大.通过该文中提到的耦合形式算法,可以较好地解决以上问题.
对于如图1 所示的模型,其分为两种域:单元微分域和有限元域,在不同域内使用不同的数值算法.但是需要注意的是,对于两个不同域之间的界面节点(图1 中红色点),为了更方便进行计算,强制其满足式(22)的伽辽金弱形式,即对于界面的单元微分单元是一种杂交元.这种耦合形式是简单明了的,不需要对强-弱耦合界面做特殊操作,也不需要对总体系数矩阵做特殊变换.
下面给出具体的刚度矩阵K以及载荷向量b的表达式,如表1 中所示.

表1 两种方法的具体刚度矩阵K 及载荷向量b 表达式Table 1 The specific stiffness matrix K and load vector b expressions of the two methods
通过以上形式,可得最终的系统方程组为

通过引入第一类边界条件,求解以上方程组,可以求得节点的位移值,并可进一步计算应力.
4 数值算例
通过本文上述所推导出的公式,将其编写成通用的Fortran 程序,并借助下面一些弹性力学的分析计算来验证单元微分法与有限单元法耦合算法的正确性.
4.1 顶部受拉的V 型缺口平板
含有V 型缺口的平板问题是一个典型的具有应力奇异点的问题.对于强形式算法,求解此类问题所得结果往往精度较差.在使用本文所给出的耦合形式算法中,在切口附近区域采用有限元算法,其他部位采用单元微分法,可以求得满意的结果.
如图3 所示的模型为一矩形平板,长度L=100 mm,宽度D=50 mm,右侧有一V 型缺口,缺口角度为30°,宽5 mm.模型下端固定,上端受y轴正向均布载荷.
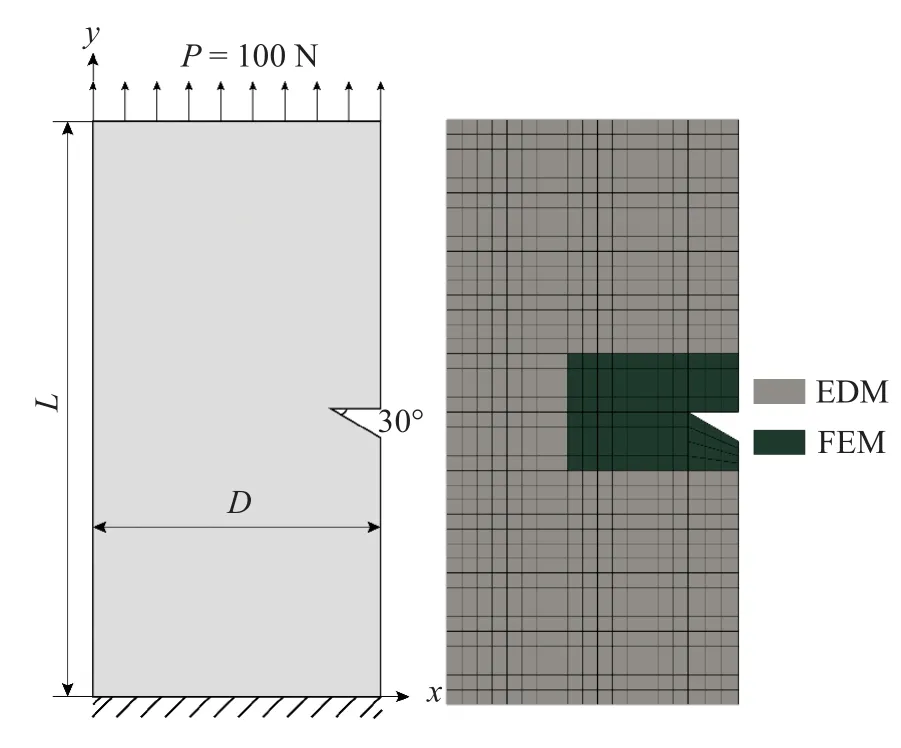
图3 顶部受拉的V 型缺口平板模型Fig.3 V-notch plate model with tension at the top
在本问题中,结构的弹性模量为200 GPa,泊松比为0.3,模型上端的载荷参数为P=100 N.在该算例中,分别利用EDM,ANSYS,EDM_FEM 耦合的方法进行计算.在使用EDM 计算时,采用二阶拉格朗日单元,单元总数为880 个,总节点数为3653 个节点,如图3 所示.同时,有限元采用商业软件ANSYS进行计算,所用单元类型为8 节点单元,网格密度和EDM 一样,单元总数880 个,节点总数为2773 个.
首先比较位移计算结果.经过计算,三种不同算法在相同网格密度下所得的y方向最大位移如表2所示.
从表2 中可以看出,传统的EDM 在计算该类问题时,所得位移结果误差较大,相较于FEM 密网格所得参考值的相对误差为3.37%.而对于文本所提出的耦合算法EDM_FEM,计算所得最大位移相对FEM 密网格所得参考值的误差仅为0.045%,可以证明该耦合算法在求解这类问题时的精度较为可靠.

表2 三种方法所得y 方向最大位移(mm)结果对比Table 2 Comparison of maximum displacement (mm)in y direction obtained by three methods
需要注意的是,针对该类问题,即使是有限元法,在不同网格密度下也会得到相差较大的结果.因此,为了进行结果的比较,采用足够密的有限元网格计算作为参考.在本文中采用ANSYS 进行计算,所用有限元网格单元数量为81 600 个.
为了比较位移计算结果,选取模型顶部y=L和中部y=L/2 处节点的位移进行比较,三种方法所得结果绘制于图4 和图5.从图中看出,FEM 和EFM_FEM 所得结果十分吻合,并和参考值吻合较好.可见模型顶部的y方向位移能够得到比较接近实际的结果,耦合的求解方法大大提升了计算的准确性.
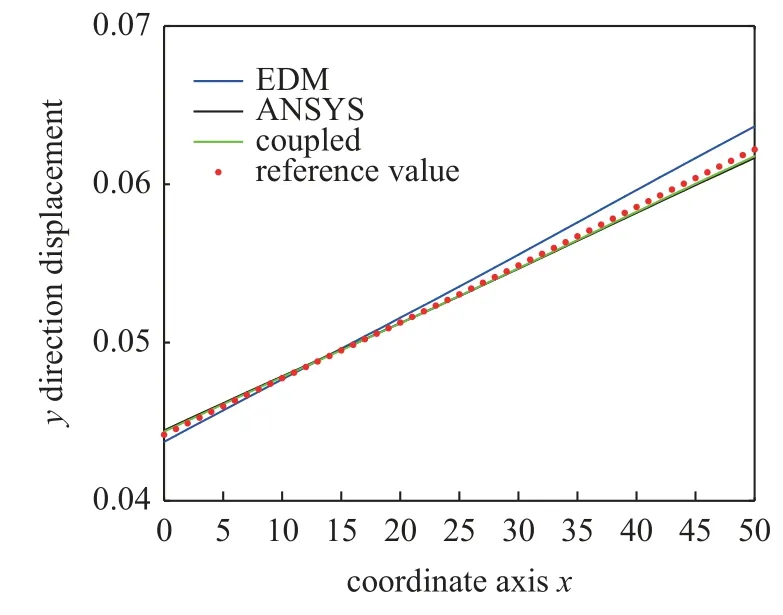
图4 顶部节点y 方向的位移Fig.4 Displacement of top node in y direction
此外,从图5 可以看出,相比于传统的EDM 形式,在应力集中区域,耦合的求解方法可以得到更加精确的结果.同时,绘制了y=L/2 线上的冯·米塞斯应力云图,如图6 所示.

图5 y=L/2 线上y 方向的位移Fig.5 Displacement in y direction on y=L/2 line

图6 y=L/2 线上冯·米塞斯应力Fig.6 von-Mises stress on y=L/2 line
从图6 中能够非常容易地看到,在V 形切口附近,模型的应力变化十分剧烈.实际上在切口尖端所得应力值应为无穷大,即应力奇异.但是在进行数值计算时,由于数值离散误差,该点附近应力变化会被磨平.在计算该类问题时,强形式算法虽然能得到较大的应力结果,但是该值的可信度不高,如应力强度因子计算值并不精确.
下面接着给出三种方法所计算的全域应力云图,如图7 所示.从图中可以看出,相较于传统的EDM,本文所提耦合形式算法计算所得尖端应力场更光滑.

图7 两种方法的冯·米塞斯应力云图Fig.7 von-Mises stress cloud maps of the two methods
就该问题而言,对于应力集中点附近的计算结果,有限元法(F E M)和本文提出的耦合算法(EDM_FEM)所得冯·米塞斯应力结果更接近于参考值.相较于传统的EDM 方法,本文提出的耦合算法(EDM_FEM)能够较大地提高算法的计算精度,得到理想的计算结果.
4.2 超燃冲压发动机燃烧室模型
作为一种强形式算法,单元微分法在形成系数矩阵时不需要进行积分计算,因此在对大规模问题进行计算时,可以节省大量的计算时间.但在用EDM 求解大规模问题时,在模型较关键部位需要用到更密的网格,才能得到较精确结果.在利用本文提出的耦合算法求解大规模问题时,可在模型的大部分采用EDM 进行计算,在关键部件采用FEM 进行计算.通过该方法,可以在得到较精确的结果的同时,提高问题的计算效率.
本算例分析一个较为复杂的三维问题,模型取自超燃冲压发动机中的燃烧室.由于模型对称,仅采用一半的模型进行分析,其结构如图8 所示,并在图中给出了模型的关键尺寸参数.

图8 燃烧室模型及其重要尺寸(单位:mm)Fig.8 Combustion chamber model and its important parameters(unit:mm)
在本算例中,如图9(a)中标号①所示为燃烧室外部框架完全固定,燃烧室内壁面受0.3 MPa 的压力,如图9(b)中标号②所示.结构的对称面(图9 中标号③所示)只固定法向的位移,两个切向的位移不受约束.

图9 燃烧室模型的边界条件Fig.9 Boundary conditions of combustion chamber model
该结构所用材料的弹性模量为200 GPa,泊松比为0.3,网格划分情况如图10 所示.可以发现模型的尾部壁面较薄,在使用纯EDM 求解时需用到大量网格,因此需在求解时将该区域利用有限元求解作为补充.由于采用两个数值方法的耦合求解,因此在图形中标注出不同算法的求解区域,绿色区域为FEM求解区域,灰色区域为EDM 求解区域.为便于比较,三种方法均采用如图10 所示的同一套网格.
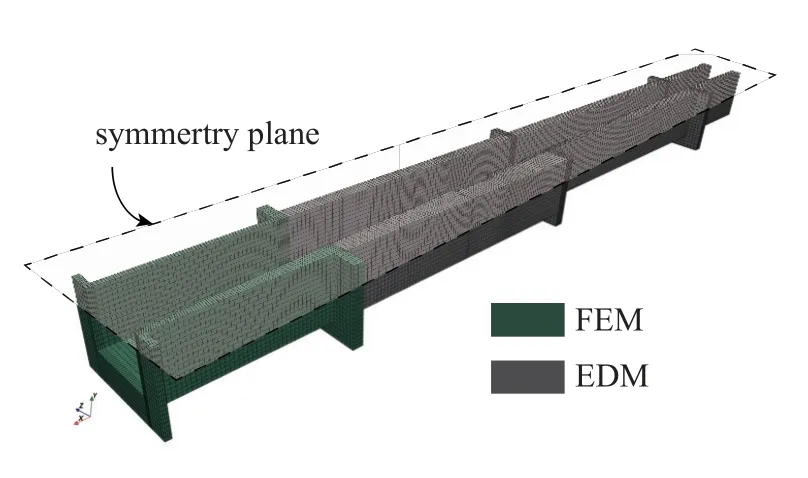
图10 燃烧室模型的网格Fig.10 Grid of combustion chamber model
网格划分为70 913 个三维27 节点单元,总节点数为641 577 个,对于此模型分别采用EDM,FEM以及EDM_FEM 的方法求解,并对如图9(b)中AB线上的节点的总位移和冯·米塞斯应力进行比较,以验证该数值求解方法的准确性.所得比较结果如图11 和图12 中所示.
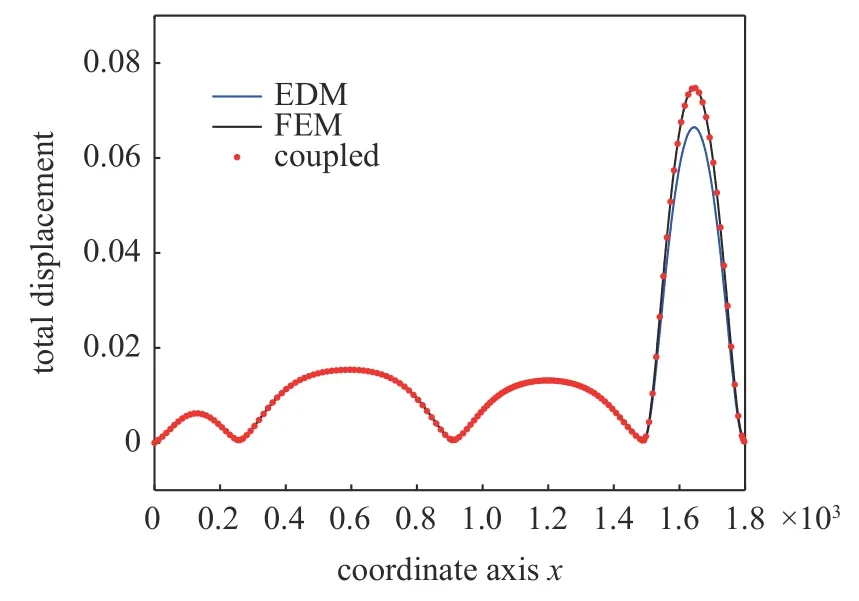
图11 三种方法在AB 线上的总位移Fig.11 Total displacement of three methods on AB line

图12 三种方法在AB 线上的冯·米塞斯应力Fig.12 von-Mises stress of three methods on AB line
从图11 和图12 中可以看出在模型尾部,传统的EDM 方法计算精度较差,而强-弱耦合的求解方法却可以得到较好的计算精度,所得指定路径上的位移和应力结果和传统有限元法十分吻合.
不仅如此,在保证计算精度的情况下,大大提高了求解的速度.为了更清晰地比较整体分析的速度,在程序中记录了组集方程及求解所用CPU 时间,并列于表3.其中CPU 采用i9-9900 k 3.60 GHz,RAM 为128 GB.

表3 三种方法组集方程及求解所用时间对比Table 3 Time comparison of three methods
由于三种方法求解方程的时间相近,不进行比较.可见强形式的EDM 方法由于不需要对控制方程进行积分,极大地降低了形成单元刚度矩阵并组装整体刚度矩阵所用的时间.在该方面,EDM 组集方程所用的时间不到有限元法的1/13.
5 结论
单元微分法是一种强形式有限元法,其在计算时不需要用到积分操作,具有简单高效等优点.但是其在处理存在应力奇异问题时表现不佳,因此,本文提出了将单元微分法与伽辽金有限元法相结合的强-弱耦合算法.针对传统单元微分法本文介绍了单元微分法和传统有限单元法相结合的耦合式算法,并给出算例验证其精度和计算效率,可得出下列结论.
(1)本文采用EDM,FEM 及耦合的求解方法进行比较分析,通过比较模型特定部位的应力和位移数据,可较为清晰地发现耦合求解方法的适用性更强.
(2)由于不需要数值积分,强形式的单元微分法在组集系统方程中所消耗的时间大为减少,有利于降低总的求解时间.
(3)由于采用单元微分法与传统有限元法耦合的方法,使能够在满足计算精度的同时显著减少计算所消耗的时间.
需要说明的是,配点法在处理力边界时比较麻烦,而且精度不高.因此可以进一步考虑在模型边界部分采用有限元离散,提高计算精度.

