黏弹性管道水柱分离弥合水锤有限体积法模型1)

王 宁 周 领 , 李赟杰 潘天文

* (河海大学水利水电学院,南京 210098)

† (河海大学长江保护与绿色发展研究院,南京 210098)

** (长江勘测规划设计研究有限责任公司,武汉 430010)

引言

水泵的启停、阀门开关以及水库水位波动等情况都可能引起管道负压,导致沿线某些位置的压强低于水体的汽化压强,此时管道中会产生蒸汽空穴,其经历生成、增长、聚集、压缩至溃灭过程被称为水柱分离弥合现象.空穴溃灭水柱弥合过程会生成高速射流、冲击波等[1],空穴的大部分能量会在此时转化为冲击波的波能[2],分离的水柱重新弥合将产生比正常瞬变流水锤大许多的升压,因此对水柱分离弥合水锤的研究十分重要[3].近年来,黏弹性管材(如PE,HDPE,PVC 等)越来越多地应用到输水线路和供水系统中,准确地模拟黏弹性管道中水力瞬变现象可为基于瞬变流理论管道泄漏堵塞检测等前沿技术提供数据,为新型管材管道设计提供依据,降低工程造价并且有效预防水锤危害.

针对长距离输水管道中水柱分离弥合水锤现象,国内外学者进行了大量模拟研究.Streeter[4]首次提出离散蒸汽空穴模型(discrete vapor cavity model,DVCM),并用于预测水柱分离过程中瞬变压力,此后许多学者[5-8]进行了研究和讨论,认为该模型在计算网格数增加时会产生不真实的压力峰值.Wylie[9]基于理想气体方程,考虑计算区段自由气体总质量来模拟均匀混合物中分布在液体中的自由气体,提出在管道任意位置空穴体积随压力而变化的离散气体空穴模型(discrete gaseous cavity model,DGCM),并认为该模型比DVCM 模拟更准确.Soares 等[10-11]将DGCM 模型用于高密度聚乙烯管道HDPE 中水柱分离弥合瞬变流现象的研究,对瞬变过程中单相流和空化流进行试验验证,并对黏弹性管道瞬变流模型的元件松弛时间及蠕变柔量等参数进行了校核.相关研究工作主要结合特征线法(method of characteristics,MOC)进行计算,有限体积法Godunov 格式因对间断、水跃和激波等结构具有良好的捕捉能力和效率,且容易扩展到高阶精度,近年来被广泛应用于水力瞬变的模拟,文献[12-13]基于有限体积法(finite volume method,FVM)二阶Godunov 格式对瞬变流问题进行模拟,并指出在相同计算精度下,与有限差分法中特征线法相比,FVM二阶Godunov 格式具有计算高效、稳定的优点对于水力瞬变过程数值模拟中常见库朗数小于1 的情况,更能体现FVM 的优越性.Zhou 等[14]通过引入压力修正系数,导出弹性管道中有限体积法的DGCM模型,成功消除了该模型在MOC 格式中因插值而出现的虚假数值振荡.

本文采用有限体积法二阶Godunov 格式对离散气体空穴模型进行研究分析,在传统的弹性管道水柱分离弥合水锤模型基础上考虑黏弹性效应的影响.将所建FVM 黏弹性瞬变流模型与试验结果以及仅考虑管道弹性的瞬变流模型进行比较,并对动态摩阻、库朗数以及初始含气率等影响因素进行了分析.

1 数学模型

有限体积法求解DGCM 模型需假定[13]自由气体集中在控制体中心,形成离散气体空穴;相邻空穴之间为纯液体,波速恒定;为计算气体空穴体积,将每一个控制体的体积平分为两等份,两个等分体内的压力及流速均由FVM 求解.根据上述基本假定,管道内空穴瞬变流的数学模型由纯水体和离散气体空穴两部分控制方程组成.

1.1 控制方程

1.1.1 水锤模型

当黏弹性管道中仅有液体时的连续方程和动量方程

式中,H为测压管水头,m;x为沿管道轴向距离,m;g为重力加速度,m/s2;V为断面平均流速,m/s;t为计算时间,s;a为波速,m/s;J为管道摩阻引起的水头损失;εr为管壁的滞后应变.

采用FVM 法求解,式(1)和式(2)瞬变流控制方程可以写成带源项的守恒性双曲方程形式[15]

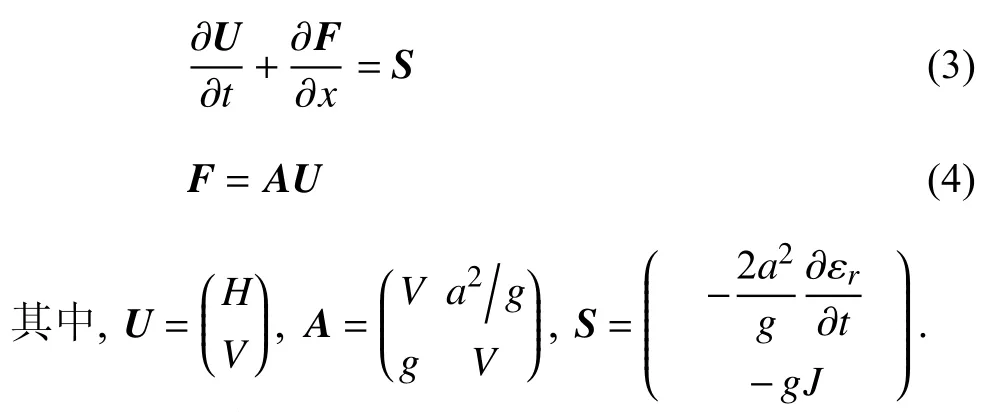
式中,U为待求的未知向量;F为通量向量;A为系数矩阵;S为源项,包含了管道的黏弹性和摩阻项.

1.1.2 离散气体空穴模型

DGCM 将自由气体的质量集中在控制体中心,可模拟自由气体在均质混合流的分布.根据理想气体方程,控制体中小体积气穴随着压力的变化而进行等温地[16]膨胀和收缩.气穴变化可表示为

式中,Qu为计算步时内平均流入截面的流量;Q为计算步时内平均流出截面的流量;∀g为气体体积.

采用FVM 法Godunov 格式计算两个等分单元内测压管水头及流量,再根据式(7)和式(8)计算空穴处测压管水头和气穴体积

式中,ρ为水体的密度,kg/m3;z为计算节点高程,m;为第j个控制单元空穴上游侧和下游侧在计算时刻的测压管水头;为第j个控制单元平均测压管水头;Hv为液体的蒸汽压头.

当两个等分单元内压强均大于水体汽化压强时,气体空穴处测压管水头取两部分均值,按式(7)和式(8)计算.此时离散气体空穴会影响等分单元内的流量变化,引入压力修正系数C_ap来考虑自由气体的影响并作出调整[17].当任一等分单元内压强降低到或低于汽化压强,则设定控制体保持液体汽化压强不变,此时,两个等分单元内压力均等于气体空穴内压力.当计算空穴体积小于0 时,空穴溃灭,继续纯液相水锤计算.

1.1.3 黏弹性效应和管道摩阻

与弹性材料不同,黏弹性管材在受力时不遵循胡克定律,产生的应变可由波尔兹叠加原理[18]描述:对于较小的应变,总应变等于相互独立的一系列应力作用下产生应变的线性相加.式(1)中迟滞应变率∂εr/∂t表示水力瞬变过程中管壁黏弹性形变随时间变化,用广义Kelvin-Voigt (K-V)模型表达,该模型将弹簧和阻尼并联看作一组元件,而管壁的应变可等效为若干组元件串联收到加载后的形变变化,广义K-V 模型示意图如图1 所示.

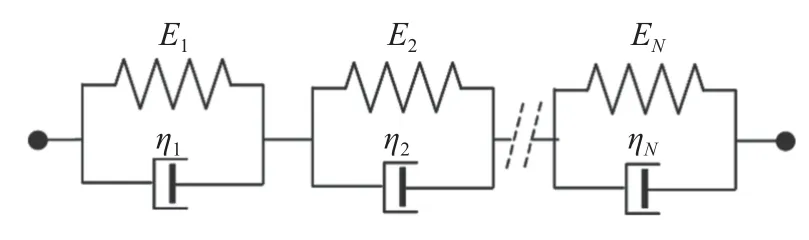
图1 广义K-V 模型示意图Fig.1 Schematic diagram of generalized K-V model

蠕变函数表达式及数值求解[19]

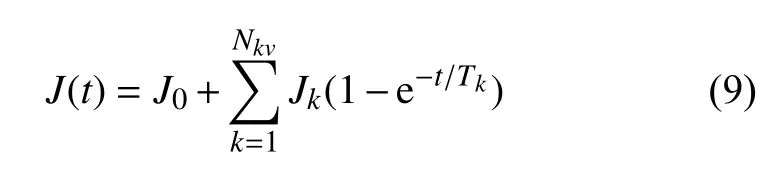
式中,Jk为第k个元件中弹簧的蠕变柔量,m2/s;Tk为第k个元件中阻尼的松弛时间,s.

式中,D为管道直径,m.

式(2)中的管道摩阻J由稳态摩阻Js和动态摩阻Ju两部分组成,其中稳态摩阻为恒定状态计算值,动态摩阻通过计算流动瞬时加速度和加权函数W的卷积得到[20].

稳态摩阻

动态摩阻

式中,ν 为运动黏滞系数,m2/s;u为在0～t之间积分的时间变量;W为关于无量纲时间 τ 的函数.

式(13)离散[21]成

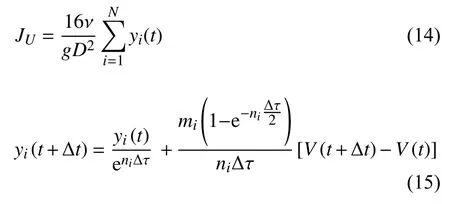
式中,yi为历史速度对当前时刻壁面剪切应力的影响;Δτ=4νΔt/D2;mi,ni为试验拟合得到的系数.

1.2 FVM 二阶Godunov 格式求解

1.2.1 数值通量计算及黎曼求解

采用有限体积法,将水锤计算区域离散为N个控制体,计算单元长度为Δx,计算时间间隔为Δt.计算区域局部离散网格系统示意图如图2 所示.

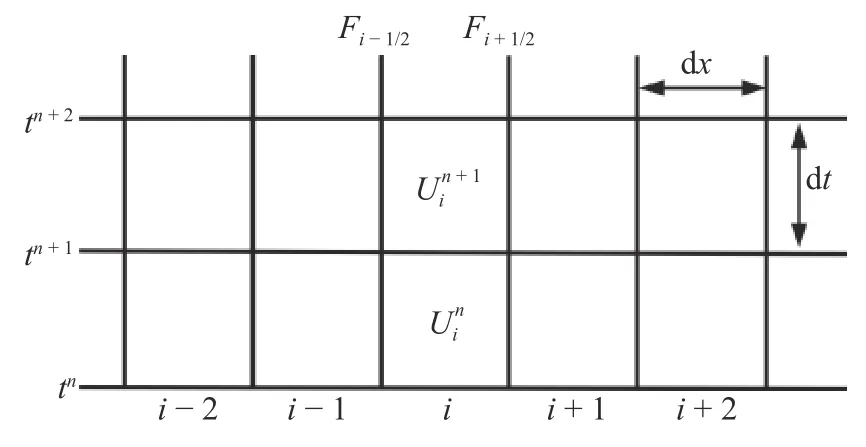
图2 离散网格系统Fig.2 Discrete grid system

从图中可以看出,任一计算单元i边界界面分别为i-1/2 和i+1/2.变量(H,V)取控制体平均值,单元体的压力、流速将通过界面i-1/2 和i+1/2 处数值通量计算,即

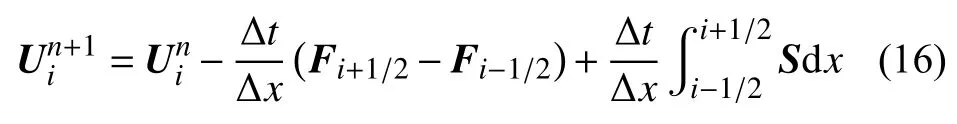
式中,n表示t时刻;n+1 表示t+Δt时刻;Fi-1/2,Fi+1/2分别表示界面i-1/2,i+1/2 的数值通量,在二阶Godunov 格式[22-23]中根据计算单元i界面处的局部黎曼问题求解,即

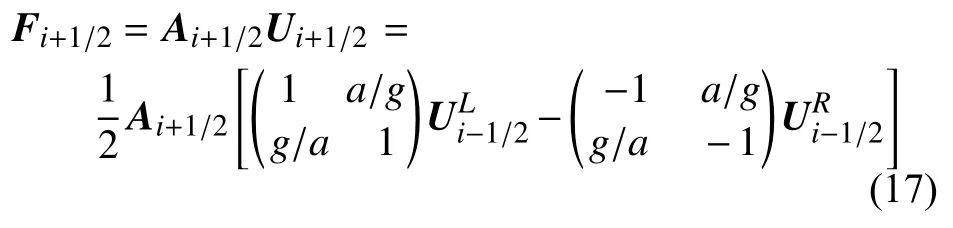
本文采用MUSCL-Hancock 法[24]进行线性重构得到二阶精度Godunov 格式,为避免线性插值中数据重构时出现虚假震荡现象,引入斜率限制器MINMOD 函数[25]

黎曼解以控制体中间区域的待求变量值来近似代替精确解

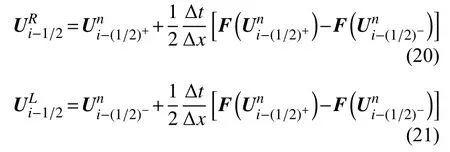
1.2.2 边界构建方法

边界处理影响数值模拟的计算精度及效率,本文采用虚拟单元法构建边界,基本思想与文献[26]相似,将边界信息直接通过计算区域体内虚拟点加以反映,可直接与已有的流体动力学求解器相结合.虚拟单元法关键在于重构虚拟点的信息,使边界信息刻画更加准确[27],最常见的处理方式是虚拟点沿着边界法向镜像外插[28].由二阶Godunov 格式可知,计算控制体变量时需与之相邻上下游各两个单元数值,通过在两端边界各增加两个虚拟控制体-1,0 和N+1,N+2,可以对边界控制体和内部控制体进行统一计算模拟,并达到二阶精度要求.其中虚拟单元0 和N+1 满足镜像外插,其数据与单元1 和N相等.

根据黎曼不变量理论[29]在计算域边界处的解析解,可推得与正负特征线相关的黎曼不变量方程.对于上游水库边界,满足虚拟单元U-1=U0=U1/2,代入=HR可得

对于下游阀门边界,虚拟单元的数据需满足UN+1=UN+2=UN+1/2

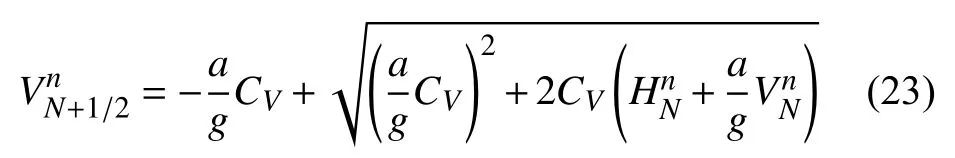
式中,CV=(V0τ)2/(2ΔH0),V0和ΔH0分别为初始时刻阀门处的流量和水头损失,τ为阀门开度

1.2.3 时间积分与稳定性约束

将源项引入非线性系统求解,考虑黏弹性项和动态摩阻项,求解精度取决于对源项的积分方式.对于二阶求解精度,采用二阶龙格-库塔法进行时间离散,其显式求解过程如下

稳定性约束条件主要包括对流项的CFL(Courant-Friedrich-Lewy)条件,以及二阶龙格-库塔离散的约束,具体时间步控制方法如下

由此可以得到

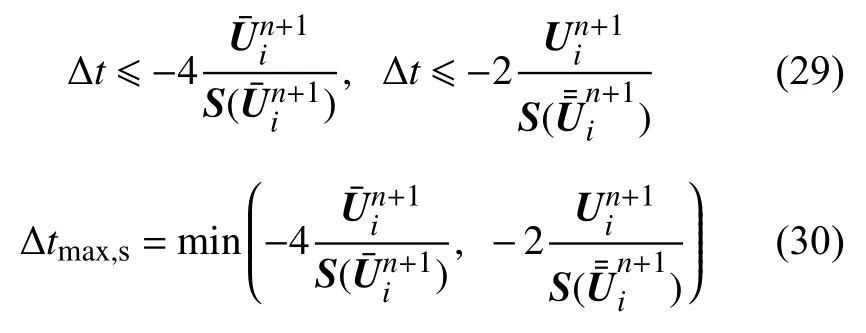
因此,计算所允许的最大时间步长需满足条件Δt≤min(Δtmax,CFL,Δtmax,s).

2 算例验证

为验证所建数学模型,以里斯本大学Soares AK 等[10]在葡萄牙搭建的试验台上测得的试验数据为依据,将本文研究的黏弹性管道中有限体积法求解纯水锤模型(FVM VE)及离散气体空穴模型(FVM-DGCM VE)与常用的MOC 算法结果、传统弹性管道模型计算结果、试验数据进行对比分析.本文引用Soares 等[10]搭建的试验装置图如图3所示.

图3 黏弹性管道试验装置图[10]Fig.3 Diagram of viscoelastic pipeline test device[10]

试验系统由水泵、空气罐、上下游阀门、压力传感器和HDPE 管道组成.管道总长度为203.00 m,内径为44.0 mm.水由水泵加压流入空气罐,保持上游压力恒定,流经上游球阀后进入水平放置的管道系统,由回水管流出.选择位于上游阀门、管道中点、下游阀门处的3 个测压点试验结果供参考校核.为分析系统中的压力瞬变,分别进行快速关闭下游阀门试验对纯水锤验证分析、快速关闭上游阀门试验对水柱分离弥合水锤验证分析.

2.1 纯水锤验证分析

工况1 为纯水体水力瞬变试验[10],系统中上游空气罐水头为35.6 m,流量为2.72 L/s,波速为315.0 m/s,雷诺数为80 000.计算时Cr=1.0,N=32.管道材料的蠕变函数常通过蠕变测试确定[19],但当黏弹性材料集成在管道系统中时,蠕变还取决于管道的轴向和环向约束,因此需基于实测瞬态压力数据进行校核.Soares 等[11]提出的系统黏弹性参数基于遗传算法和Levenberg 算法两步逆模型确定.经校核发现当取3 组Kelvin-Voigt 单元可以较好拟合蠕变曲线,各元件松弛时间及蠕变柔量的取值为τ1=0.018 s,J1=0.256 GPa-1;τ2=0.50 s,J2=0.256 GPa-1;τ3=3.0 s,J3=0.256 GPa-1.为验证模型的有效性,选择工况1 的试验数据与本文模型计算值、MOC 模拟结果进行对比,结果如图4 所示.

图4 工况1 下游阀门处计算值与试验结果Fig.4 Calculation value and test result at downstream valve in Case 1

采用工况1 研究不同Cr的影响,图5 分别给出阀门处MOC VE 及FVM VE 模型压力计算的结果.

图5 库朗数对计算结果的影响Fig.5 Influence of Cr on the calculation result

由图4 可知,工况1 数值模拟的最大峰值比试验测得数据略高,可能由试验关阀时间比数值模拟采用的时间稍大造成.FVM VE 模型与MOC VE 模拟的阀前水锤结果基本一致,总体上与试验压力波动曲线在极值、相位上能较好地吻合,根据图4 结果可认为,本文模型能准确模拟试验压力波动整个过程.

图5 中,计算中库朗数Cr分别取1.0,0.5,0.1.图5(a)结果表明:在MOC 求解格式下,随着Cr的减小,计算压力波动结果出现了明显的数值耗散,这是由于传统MOC 计算方法只有一阶计算精度.图5(b)结果显示:随着Cr减小,压力波动只产生了轻微的数值衰减的现象,有限体积法二阶Godunov求解格式具有二阶精度,本文模型在Cr小于1.0 时仍然能保证数值模拟结果的稳定性和准确性.

在输水管道中管道摩阻和黏弹性效应均可引起瞬变压力衰减,考虑动态摩阻UF 的有限体积法黏弹性模型FVM VE+UF 与考虑稳态摩阻的FVM VE 模型计算结果如图6 所示.

图6 动态摩阻对计算压力的影响Fig.6 Influence of dynamic friction on calculated pressure

由图6 可知,在黏弹性输水管道瞬态压力计算中,动态摩阻的影响不再明显.这是因为实际情况中影响管道因素还有流体的轴向运动、管道锚固约束、流体惯性效应等,因此校核得到的蠕变函数不一定仅代表HDPE 管壁准确黏弹性效应[30],而是包含动态摩阻等阻尼效应的组合.在瞬变流过程中,由于黏弹性效应造成的管道压力衰减太快[31-32],瞬变流持续时间短,因此关阀完成后管壁摩擦做功时间短,做功较少[33].综上所述,在黏弹性管道水力瞬变压力衰减过程中,黏弹性效应相比于非恒定摩阻起主要作用,在后续计算中将不再考虑动态摩阻的影响.

2.2 水柱分离弥合水锤验证分析

工况2,3 为水柱分离弥合试验[10],系统中上游空气罐水头为30.6 m,波速287.0 m/s.计算时Cr=1.0,N=32,松弛时间及蠕变柔量取值τ1=0.10 s,J1=0.60 GPa-1;τ2=0.50 s,J2=0.35 GPa-1;τ3=3.0 s,J3=0.50 GPa-1.其中工况2 流量为3.00 L/s,雷诺数为87 000;工况3 流量为4.00 L/s,雷诺数为1.2×105.选择工况2 验证水柱分离弥合水锤现象.试验初始流态没有出现分布式气泡,故采用建议较小的初始含气率.

已有学者[17,34]讨论采用MOC-DGCM 模型模拟时初始含气率α0的变化对计算压力产生的影响,且表明较小初始含气率α0≤10-7时能较好地模拟试验结果.本文FVM-DGCM VE 模型基于上述理论,对比α0分别为10-7,10-8,10-9时阀门处计算压力,如图7 所示,结果表明:当初始含气率低于或等于10-7时,计算结果基本一致,因此后续计算中,α0均取为10-7.

图7 FVM-DGCM VE 中α0 对上游阀门压力的影响Fig.7 Effects of α0 in FVM-DGCM VE on pressure at upstream valve

图8 是为关闭上游阀门时阀门处试验测得的压力-时间曲线与数值计算结果对比,模拟考虑压力降低到蒸汽压时汽化发生的水柱分离现象.

如图8 所示,FVM-DGCM VE 模型模拟的阀后水锤与传统算法MOC-DGCM VE 计算结果在每个周期内极值接近,随着瞬变流的进行,MOC-DGCM VE 模型中的相位差不断累积,使得模拟结果相位提前于试验压力曲线现象逐渐明显,综上所述,FVMDGCM VE 能更为准确地模拟出试验的压力峰值、波动周期.

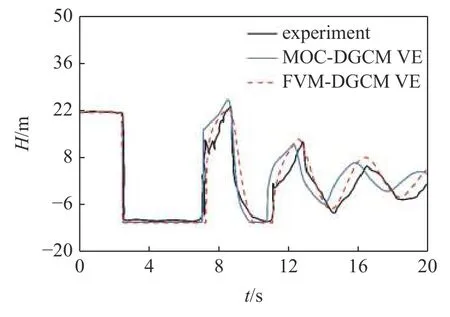
图8 工况2 上游阀门处计算值与试验结果Fig.8 Calculation value and test result at upstream valve in Case 2

图9 中三条曲线分别是试验实测曲线、考虑管道黏弹性以及仅考虑管道弹性时的水柱分离弥合现象模拟结果.

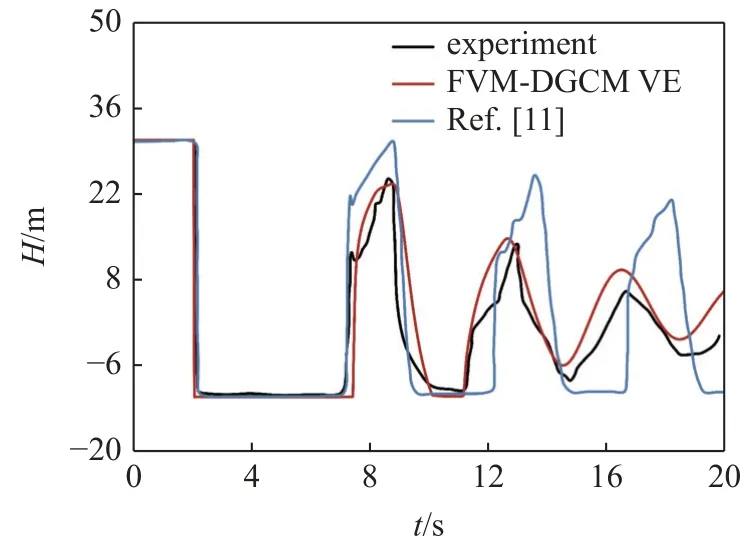
图9 工况3 上游阀门处计算值与试验结果Fig.9 Calculation value and test result at the upstream valve in Case 3

由图9 可以看出,在相位变化上,考虑管道黏弹性的水柱分离模型模拟结果与试验结果吻合较好,而弹性管道模型在后续周期中与试验结果相差较大.在压力波峰值上FVM-DGCM VE 计算得到的相对误差值为3.34%,模拟结果更接近试验结果,而弹性管道模型结果相对误差值为25.15%,振幅值偏大.从压力波振幅值和相位变化综合来看,考虑管道黏弹性的水柱分离弥合瞬变流模型的模拟结果更接近实测数据.

3 结论

本文基于有限体积法二阶Godunov 求解格式,针对水柱分离弥合水锤现象,建立了考虑管道黏弹性的离散气体空穴模型进行研究分析.将本文模型计算结果与试验结果以及弹性管道瞬变流模型计算值进行比较,分析了动态摩阻、库朗数及初始含气率等因素的影响,主要得出以下结论.

(1)本文建立的考虑黏弹性效应的有限体积法求解水柱分离弥合水锤模型能够准确模拟出纯水锤和水柱分离弥合水锤两种情况的瞬变压力,均与试验数据高度吻合.

(2)与已有的特征线求解模型相比,本文建立的有限体积法求解水柱分离弥合水锤模型更具稳定性和准确性.当库朗数Cr小于1 时,特征线模型会产生严重的数值耗散现象,且MOC-DGCM VE 模型模拟结果相位提前于试验压力曲线,本文模型能更准确地模拟试验压力波动曲线.

(3)在黏弹性管道水力瞬变压力衰减过程中,黏弹性效应相比于非恒定摩阻起主要作用.在水柱分离弥合数值模拟过程中,当初始含气率低于或等于10-7时,计算结果基本保持一致,因此对于较小的初始含气率,α0可取为10-7.

(4)对于黏弹性管道中的瞬变流现象,考虑管道黏弹性可显著提高模拟准确性.黏弹性管道瞬变流模型模拟结果能较好地与实测数据相吻合,而弹性管道瞬变流模型模拟的结果在压力波的振幅、相位变化等方面都与试验结果有较大的差异.