极高超声速稀薄气体原子辐射效应的p-DSMC 方法

杨全顺 方 明 ,1) 李埌全 粟斯尧 杨彦广

* (中国空气动力研究与发展中心超高速空气动力研究所,四川绵阳 621000)

† (中国空气动力研究与发展中心,四川绵阳 621000)

引言

气动加热是高超声速飞行/再入不可回避的问题之一.飞行器在第一宇宙速度以上的极高超声速再入/飞行过程中,头部激波层气体会变成对飞行器加热的强辐射体,辐射的光子会显著增强气动加热效应,辐射加热随着速度的增加逐渐变得重要.研究表明,飞行速度超过10 km/s 时[1-5],辐射加热占对流加热的30%左右,此时,飞行器的热防护设计不仅需要考虑对流加热、催化加热等非辐射加热[6-8],还需要考虑辐射加热[9-12].

为准确计算非平衡流动中的辐射,NASA 很早开发了非平衡空气辐射(NEQAIR)程序[13].在NEQAIR 程序中,准稳态假设用于确定非平衡气体组分的激发态布居,被认为是非平衡流动的最佳逐线法(LBL)解算器.然而,NEQAIR-LBL 程序包含一个一维正切平板辐射输运解算器,其成本非常昂贵,不适合二维或三维的辐射计算,此外,高分辨率的逐线方法计算需要数十万个辐射输运方程(RTE)解,也是计算二维或三维辐射成本太高的另一个因素.在这种情况下,光子蒙特卡罗方法(PMC)[14]应运而生,在此方法中,辐射传输通过允许每个网格以光子束的形式向随机方向发射其能量来建模,对非灰辐射场更精确、更有效.之后,Ozawa 等[15]使用直接蒙特卡罗方法(DSMC)和PMC 松耦合模拟了原子在超高速再入流动中的辐射.我国学者在高温气体热化学非平衡流动,开展了大量关于非平衡流动、传热问题的理论研究[16-19],但对非平衡辐射特性理论建模研究很少.

在实验测试方面,Brandis 等[20]在地球大气环境中,对激波速度8.0～11.5 km/s 的真空紫外至近红外的空间、光谱分辨的辐射强度进行测量,与数值结果对比发现,在不同的激波速度下,LAURA(兰利气动热力学迎风松弛算法)/HARA(高温气动热动力学辐射)辐射热流计算结果都有不同的高估和低估,试验数据与理论模拟的偏差表明计算模型仍需完善.之后文献[21]又以激波速度4.7～8.0 km/s 的混合气体及纯N2进行了辐射强度的测量,发现新的实验数据不仅高于以往的实验值,而且个别的新实验值甚至高出了一个量级,这表明,假设以现有的实验数据进行数值模拟,结果也是不准确的.2017 年,Cruden 和Brandis[22]测量了光谱范围190～1450 nm的空气非平衡辐射后发现,不同反应速率的DPLR/NEQAIR 对实验数据的复现结果较差.同年,Brandis等[23]研究发现,激波速度8.0～11.5 km/s 的大气再入环境下,NEQAIR 和HARA 的预测结果低于电弧激波管(EAST)测试的结果.综上,近年来的辐射实验和理论模拟研究表明,目前的流动和辐射计算模型不确定性仍然较大,并且部分实验数据有待进一步完善.

基于以上的分析考虑,本文基于优化的原子辐射模型,提出p-DSMC 方法,研究了有无激发辐射效应影响下的壁面压力和热流以及沿驻点线变化的平动、振动和转动温度.文章的组织如下:第二部分简要介绍计算模型和激发、辐射模式,第三部分是模型的实现与验证,第四部分是对全文的总结.

1 辐射效应的DSMC 建模

1.1 DSMC 方法

目前,Bird[1]发展的DSMC 方法是求解稀薄流域高超声速飞行器非平衡气体绕流最可靠的计算工具.对于稀薄流域,由于连续介质模型失效,N-S 方程的有效性存疑,而求解玻尔兹曼方程对于巨大粒子量的真实气体又过于复杂,尤其是对于碰撞项的积分求解.DSMC 方法用一个仿真分子代表一定量的真实气体分子,并将分子运动与碰撞解耦,借助现象学模型和统计方法,实现流场参数和物体壁面属性的直接计算.DSMC 的详细陈述可见参考文献[24],其有两个基本要求:一是网格尺寸须小于分子平均自由程,二是时间步长须小于分子平均碰撞时间.

1.2 稀薄气体原子辐射模型

1.2.1 原子能级模型

原子辐射模型最理想的情况是在原子辐射过程中涵盖所有的原子能级.然而,辐射态的数量如此之多,以致于反应的数量会是一个大的未知因素.另外一个问题是大量辐射可能来自原子布居稀少的能级,而对于实际数量的模拟分子来说,这些跃迁很少发生,以至于辐射的统计散射会大得令人无法接受[1].早期的文献[25]提到,上述问题可以通过现象学模型解决.

原子辐射呈现出一个更困难的问题是电子态的数量和辐射跃迁的数量大于分子的相应数量.计算上是可行的,但就计算机内存需求而言,这是一个重大的灾难.Park[13]和Bird[1]分别提出了原子能级群组的思想,原子能级使用数字来代替光谱项表示,这样有利于简化能级.还有一个需要注意的问题是,能级的数量和计算时间是密切相关的,因为我们在辐射部分提到,亚时间步长必须要小于选取能级中最小的能级辐射寿命.Taylor 等[4]也在文献中明确提出,在原有DSMC 代码中加入激发辐射模块后,计算时间要更久.但是,这不是最主要的问题,在激发辐射中最关心的问题应该是选取的激发辐射路径对辐射加热的影响,这是因为,原子的电子能级众多,可选则的能级群组方式也多,但能级之间的跃迁必须要满足选择定则,此外,能级之间的跃迁即使不是禁戒的,也有强弱之分.Bird[1]和Park[13]在文献中也对N,O 原子能级的选择给出了建议,因此,在综合考虑后,我们选择了7 能级群组,这也与飞行试验观察到的典型谱线特征吻合.本文使用“7”能级结构如表1 所示.

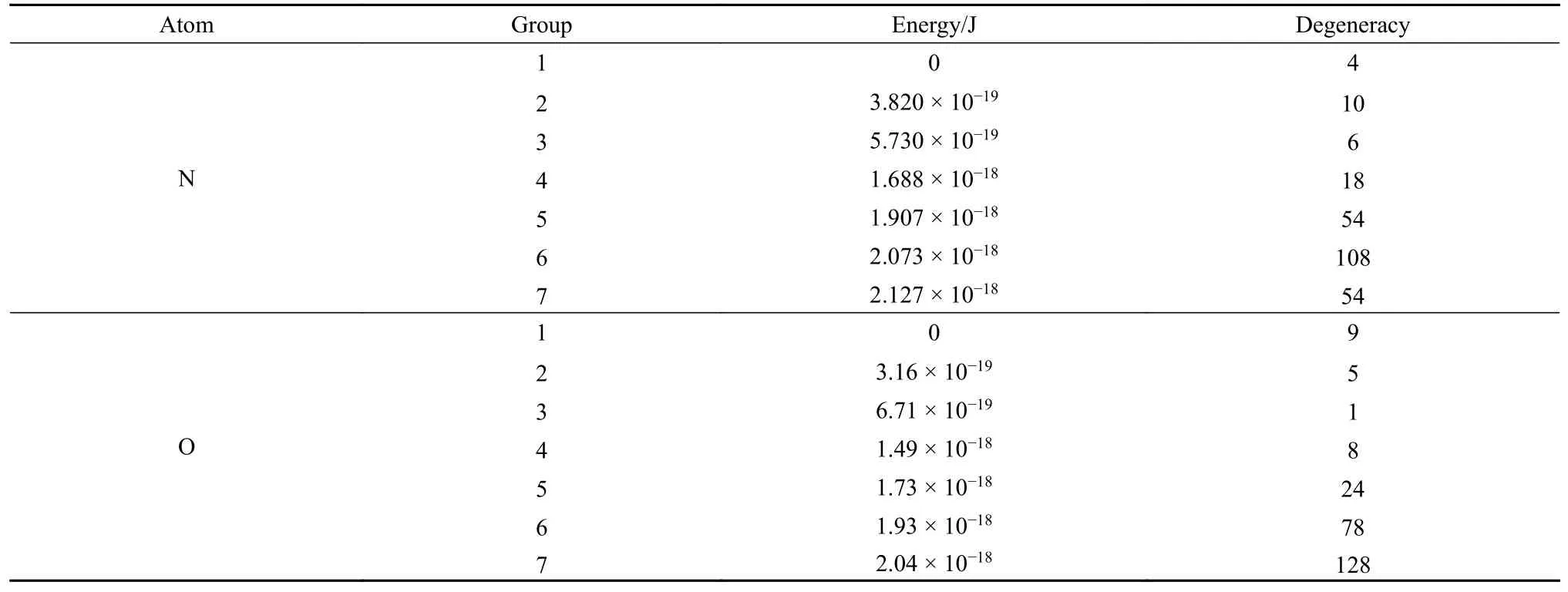
表1 N,O 原子群组能级的能量和简并度Table 1 Energy and degeneracy of energy levels of N and O atomic groups

1.2.2 原子的激发

(1)原子-原子碰撞激发的物理模型

原子-原子碰撞激发的过程以原子分子反应静力学[26]为基础.Gallis 和Harvey[27]没有明确提出这种说法,但他们提出的原子-原子碰撞时形成伪分子的思想却与原子分子反应静力学理论不谋而合.比如N 原子,其基态为4S,运用原子分子反应静力学原理,形成N2分子基态的过程为

假如其中的一个为激发态或两个都是激发态,则形成N2分子的低/高激发态,例如

式中的数字代表自旋多重度,S,P 表示原子的电子态,Σ,Π,Δ 表示分子的电子态.

(2)原子激发路径

原子能级运用群组的概念将导致能级不再使用光谱项表示能级,致使能级之间的跃迁不再严格地满足各种选择定则.各能级之间还是存在允许跃迁和禁戒跃迁,但目前的7 能级群组不存在这种情况,即

因此,碰撞对在满足:①激发条件、②激发概率、③原子布居概率的情况下,原子可以从低能级向上跃迁到其他各个能级群组.

(3)原子的激发条件和概率

对于DSMC 方法来说,任何一个事件都是以一定概率发生的,原子与原子的碰撞激发也不例外.

对于选中的能够碰撞的原子对,应该满足下面的激发条件

其中,Etrans是碰撞对的相对平动能,Eu-El是跃迁能级的能级差.

由于在原子的激发过程中,标记每个原子作为一个单独的态,所以,激发概率可以表示为[1]

式中,σex为原子-原子碰撞的激发截面,σcoll是弹性碰撞交叉截面.鉴于激发截面数据的不完整性和不可靠性,Bird[1]使用定性的手段,即电子与原子的弹性交叉截面(σcoll)量级是10-15cm2,而电子碰撞的激发交叉截面(σex)量级为10-16cm2,电子-原子碰撞的激发碰撞截面和总碰撞截面的比值为0.1,并使用概率常数作为激发概率.本文借用Bird 的思想,也选用概率常数,选取原子-原子碰撞截面比值为200-1.

(4)原子的能级布居

满足原子激发条件,并且激发概率大于随机数的原子激发到哪个能级,也是必须考虑的问题.分子或原子的第j电子态能级能量高于低能态的平衡分数由玻尔兹曼分布给出

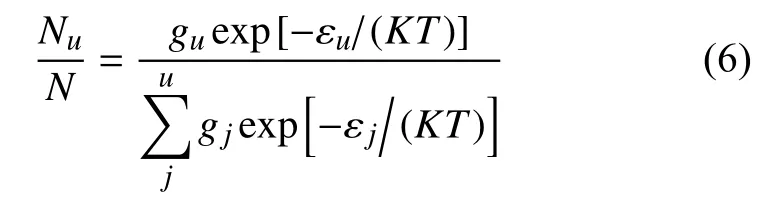
式中,gj是高能级的简并度,N为低于Ej的原子布居数,T为有效温度并满足下式

处于Ei能级上的原子被激发,假如随机数小于该分数,则原子将被激发到Ej能级.

1.2.3 辐射模型

对于辐射,本文只涉及到了束缚-束缚态之间的自发辐射.在10 km/s 左右的来流条件下,虽然能量已经很高了,驻点区的温度达到了2.0×104K,但相较于等离子体环境,能量还是偏低,因此,束缚-束缚电子态之间的跃迁产生的辐射是最明显的.即使在当前的情况下有其他的两种跃迁,但其跃迁强度较之束缚-束缚的跃迁强度都较弱,对其模型壁面的辐射加热可忽略.之前文献[5]也和本文的处理方式一致;当然,本文是我们前期计算辐射热流的一种方式,对于更高再入速度下的辐射特征,其他两种跃迁可能是重要的,这将作为我们后续的工作之一.

处于激发态上的原子拥有寿命,当模拟的时间步长大于其自发辐射寿命时,原子将以一定的概率自发辐射回到低能级态.

(1)辐射路径

本文采用N,O 原子7 能级群组进行自发辐射跃迁.涉及到的跃迁能级已罗列在表2 中,路径呈现于图1.需要注意的是,Bird[1]已经证实,只有表2中涉及的能级跃迁才拥有较强的光谱,但本文在此添加了N 原子低激发态2 和3;O 原子低激发态4,3 和2,希望可以获得更精确的辐射加热数据,相应的信息也一并列于表2.

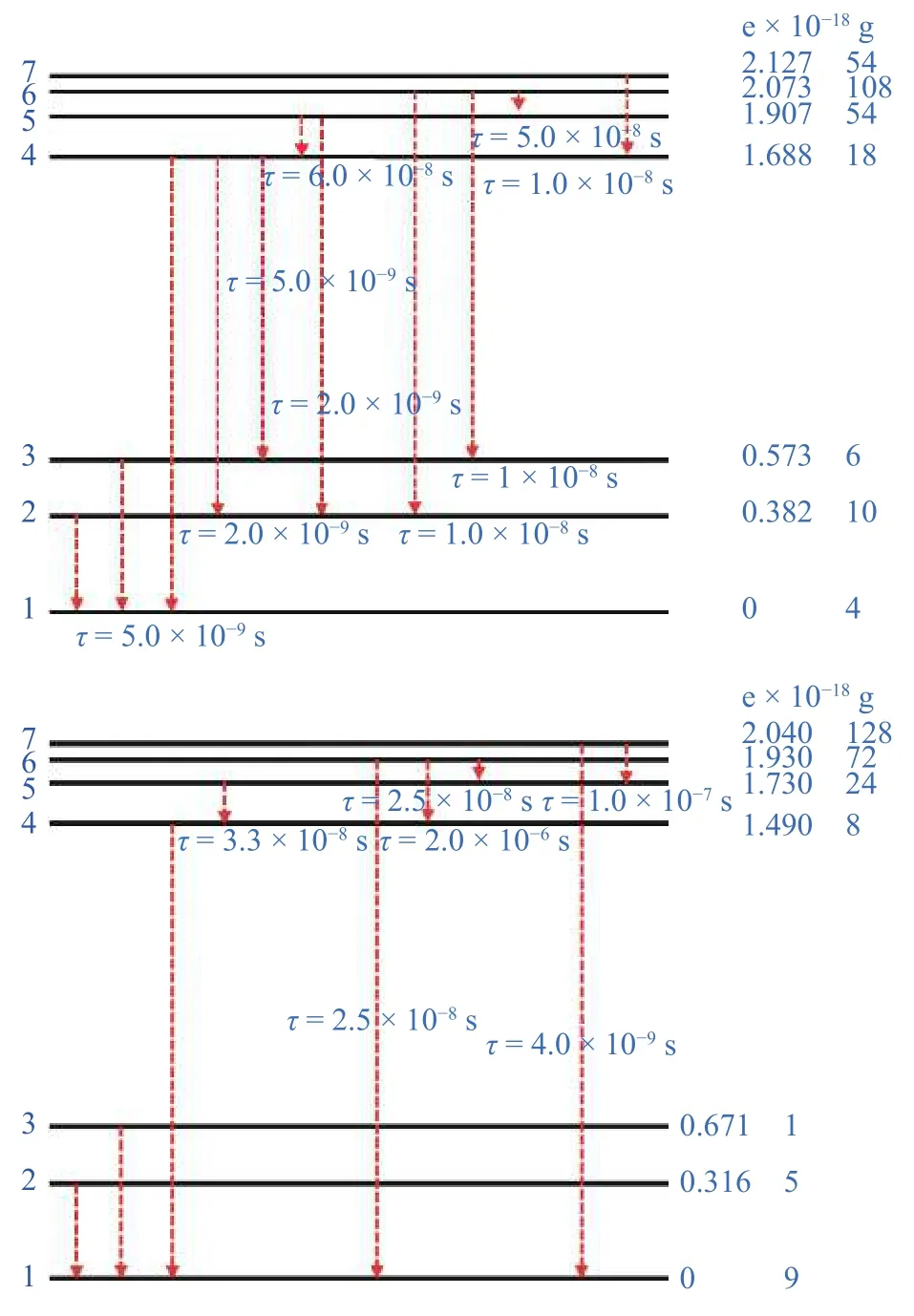
图1 N(上)、O(下)原子群组能级跃迁Fig.1 Energy level transition of N (upper)and O (lower)atomic groups

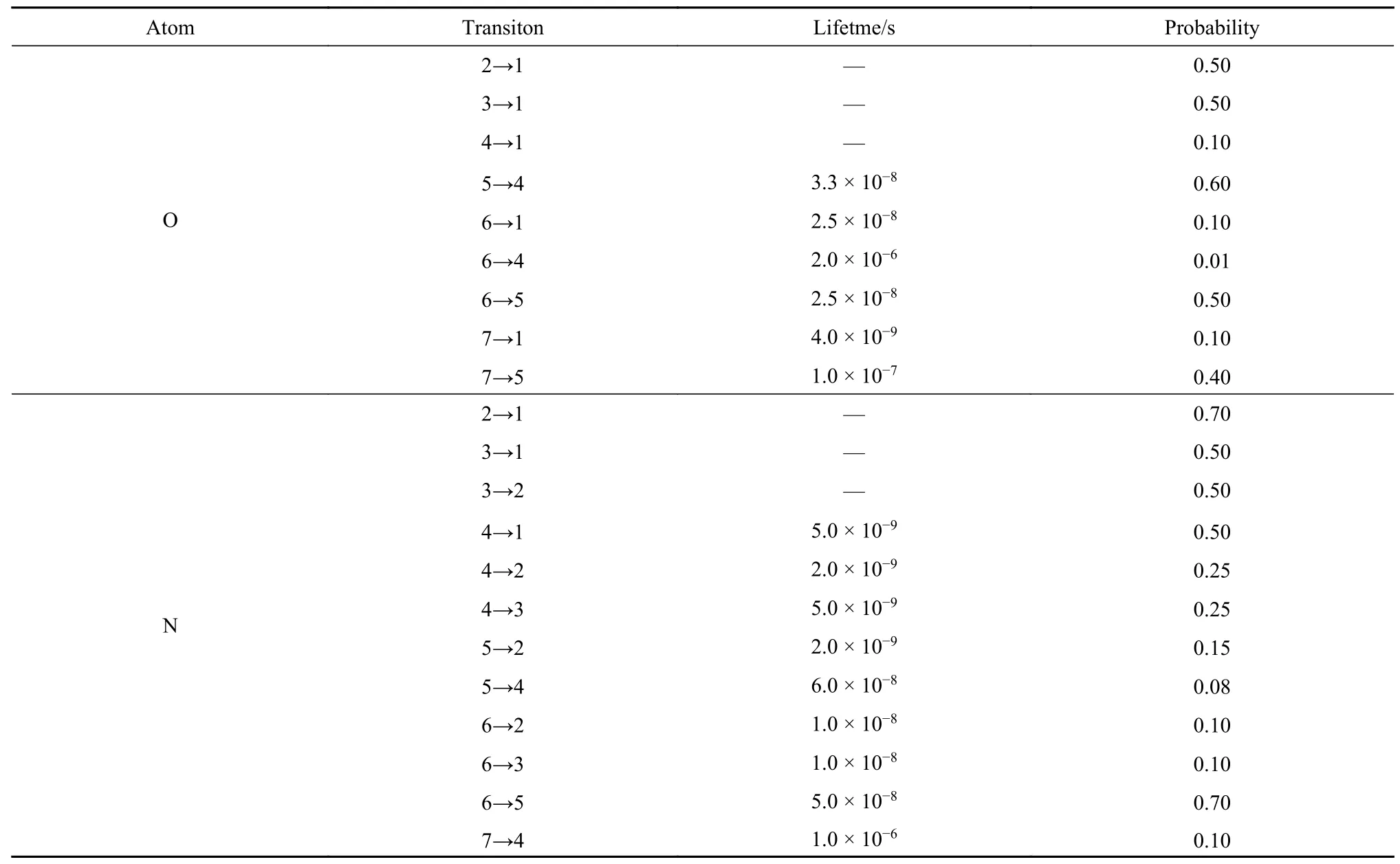
表2 N,O 原子群组激发态的辐射寿命和跃迁辐射几率Table 2 Radiation lifetime and transition radiation probability of excited states of N and O atomic groups

(2)辐射条件和概率

在原子的激发模型中已经提到,由于此时的能级不是使用光谱项而是数字表示,所以,能级之间的跃迁不再严格遵守选择定则.但本文所选取能级的标准是能级之间不存在禁戒跃迁,处于高能级的原子可以向任意低能级进行自发辐射跃迁.需要注意的是,DSMC 选择的时间步长远大于能级的自发辐射寿命,假如选择粒子的运动时间步长,则会导致大量的光谱线消失.因此,在DSMC 中添加辐射模块时必须使得光子的运动时间步长小于7 能级中最小的辐射寿命.光子的时间步长大于能级的辐射寿命时,释放出光子,即辐射条件为

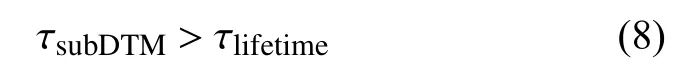
正是由于每个能级表示的是能级群组,低能态跃迁是以一定的份数跃迁,本文将此份数作为自发辐射跃迁的概率(P).涉及到的跃迁路径,哪个那级的自发辐射路径的概率大于随机数,原子将自发辐射回到该低能级.

1.2.4 光子追踪

在目前的计算工况下,光子速度大于流场中粒子速度四个数量级,假如光子以粒子运动的时间尺度向前运动,追踪光子是及其困难的.因此,本文采用亚时间步长的思想,在一个亚时间步长内,将光子的运动距离控制在一个网格宽度内.这样做的优势在于,不仅可以追踪到光子的轨迹,而且可以减少内存分配.

光子追踪的另一问题是跨进程并行,如图2 所示.采用亚时间步长解决了光子追踪问题,但光子运动的最终时间是一个时间步长.在一个时间步长内,光子肯定跨越好几个进程进行运动.本文中已经使用MPI 的光子跨进程并行程序,最大核数测试达到500 个核,并行效果良好.

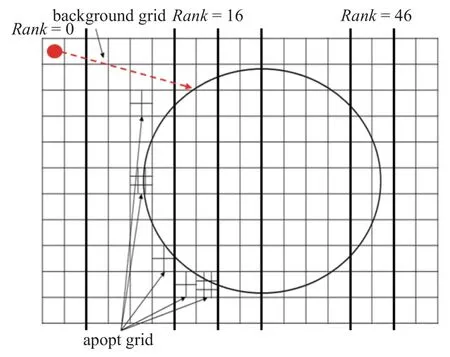
图2 光子追踪示意图Fig.2 Photon tracing diagram

2 p-DSMC 方法验证及辐射效应影响验证

本文使用列于表3 中的初始流场条件(包括数密度N0、温度T0、马赫数Ma、壁温Twall和密度ρ),相当于大气高度86 km,壁面为全漫反射,涉及19 化学反应,运用p-DSMC 方法得到了二维圆柱绕流的流场分布.在p-DSMC 模拟中,流场涉及5 组元,每个网格中初始分布20 个模拟粒子,按照沈青[28]建议,网格宽度取大约1/3 的平均自由程,时间步长为1×10-7s.

表3 流场的初始参数Table 3 Initial parameters of flow field

2.1 不含辐射效应的DSMC 代码验证

使用已建立的DSMC 代码MONACO[29]和dsmcFoma[30]与目前的p-DSMC 代码进行比较,MONACO 和p-DSMC 代码均采用TCE 化学模型[31],而dsmcFoma 使用D-K 化学模型[32].在所有的例子中,转动和振动碰撞数分别设置为5 和50.在考虑化学反应且速度为6.7 km/s 时,基于表3 中的来流初始参数,在不包含N,O 原子的激发和辐射时,获得了二维圆柱壁面的压力和热流,并与之前的模拟结果[29]进行了比较,二者符合的很好.壁面的压力和热流误差均在5%以内,尤其是在驻点位置,误差在1%以内;另外,获得的平动、振动以及转动温度均与文献结果符合较好,这些信息也可以从图3中看出.此外,从图3 中可以看出,由于MONACO与本文使用相同的化学反应模型(TCE),因此,壁面压强和热流都更接近MONACO 获得的值.

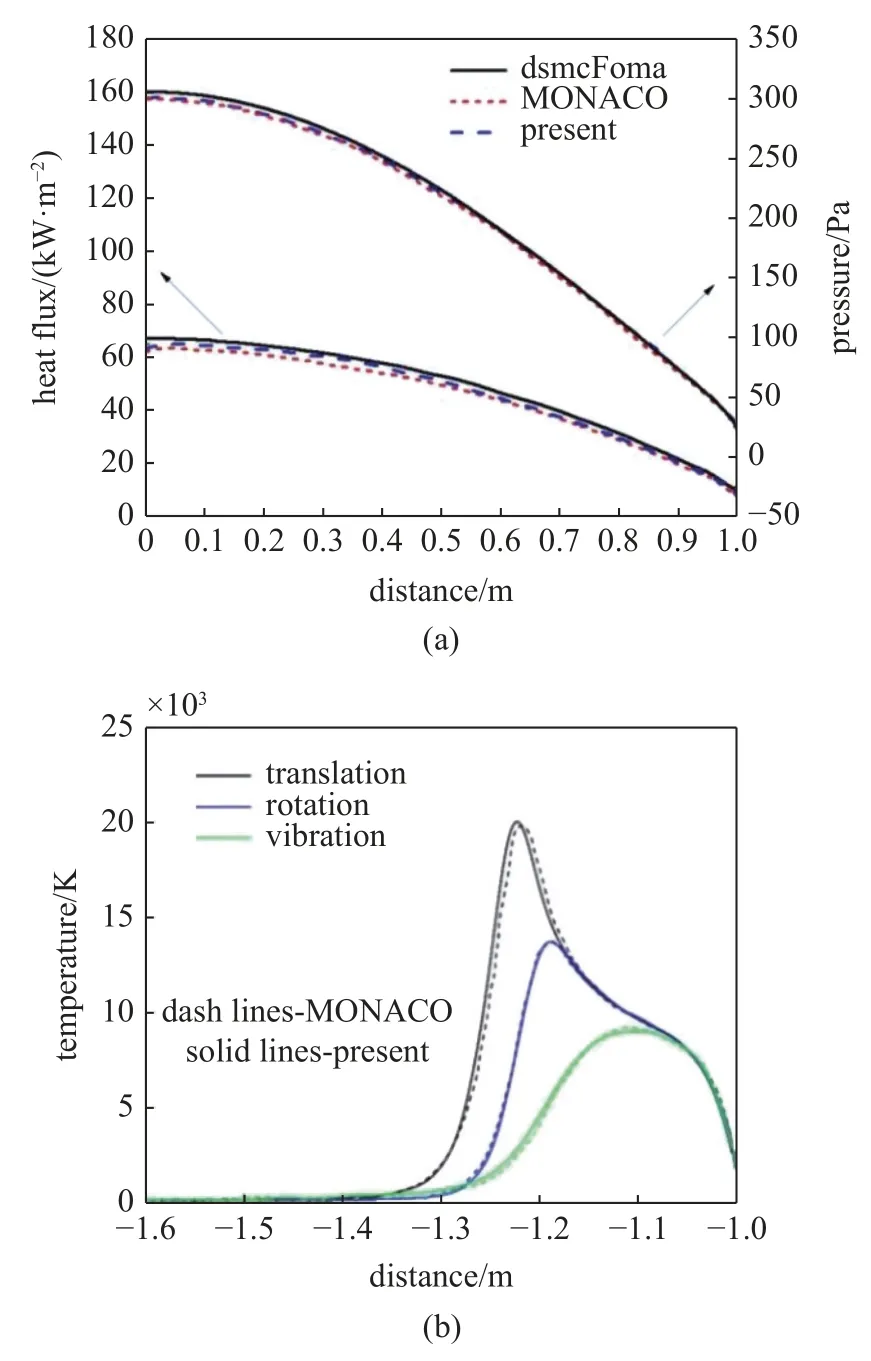
图3 马赫数24.58 时,(a)沿壁面的热流和压力以及(b)沿驻点线变化的平动、转动和振动温度Fig.3 (a)Heating flux and pressure on wall and (b)translational,rotational and vibrational temperatures along the stagnation line at Ma=24.58

2.2 辐射对流场性质的影响

在流场条件不变的情况下,图4 和图5 分别展示了考虑原子辐射效应后对流场全局温度、平动温度和内部模态温度的影响.从图4 中可以看出,随着马赫数的增大,辐射对流场的影响越大,马赫数越大时,热流最大区越靠近壁面.这种效应与图6 所示的向右速度偏移所表明的差异一致.对于非平衡气体,全局温度定义为平动温度和内部模态温度的加权平均,因此,图5 呈现了平动、转动和振动温度在马赫数增大时辐射对其产生的影响.从图5 可以看出,辐射对平动、转动和振动温度的最大值几乎没有影响,但随着马赫数的增大,平动温度和转动温度都有靠近驻点的趋势,这与整个流场展示的全局温度相对应.图5 呈现的现象与文献2 给出的平动、振动和转动温度的变化规律是一致的,即在考虑了辐射效应后,平动和内部模态温度均没有发生很大改变.

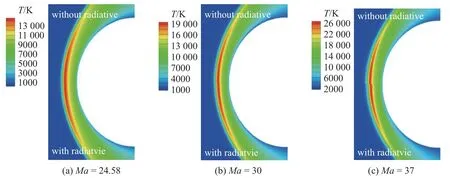
图4 原子辐射效应对流场的影响Fig.4 Influence of atomic radiation effect on the flow field

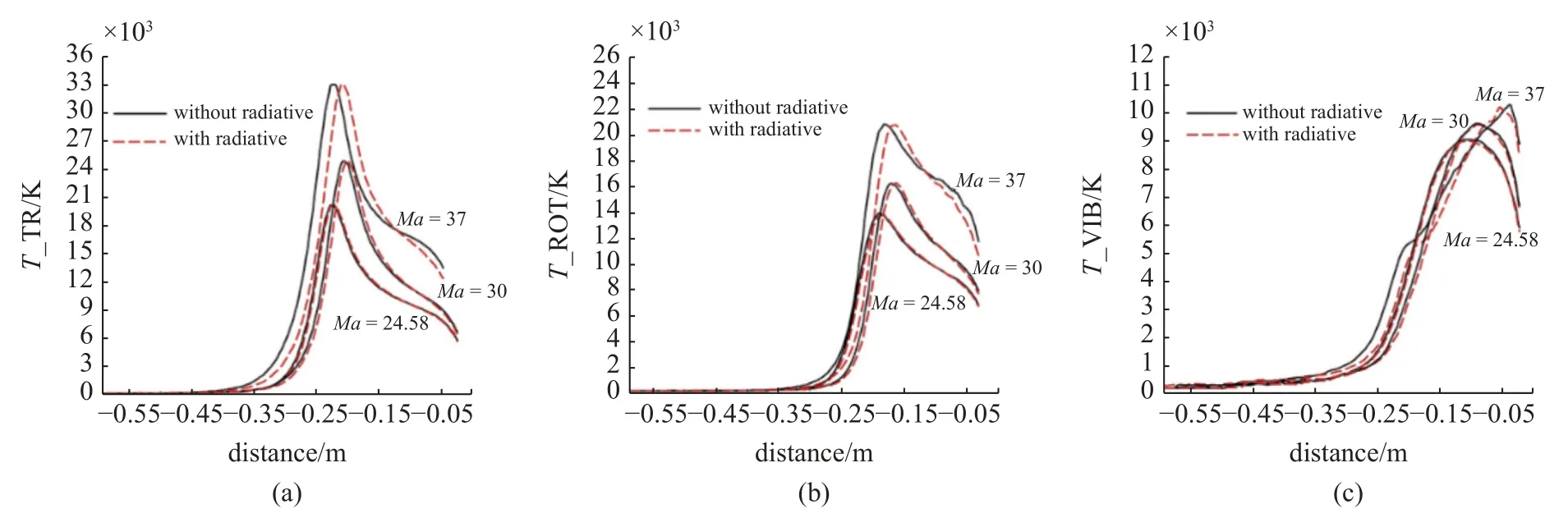
图5 原子辐射效应对(a)平动、(b)转动和(c)振动温度的影响Fig.5 Influence of atomic radiation effect on the (a)translational,(b)rotational and (c)vibrational temperature

图6 原子辐射效应对速度的影响Fig.6 Influence of atomic radiation effect on the velocity

2.3 辐射效应对壁面热流的影响

图7 是考虑了N,O 原子激发和辐射后壁面的辐射加热和对流加热沿流场中心线的变化规律.从图7 中可以看出,辐射热和对流热有相似的变化趋势,即随着远离驻点区,辐射加热变得越来越小,并且辐射热流减小的速率要大于对流加热.这是因为在背风区,温度降低,粒子能量减小,碰撞导致分子的解离减少,致使原子浓度变少,圆柱壁面辐射加热相应减小.这说明流场内原子浓度是影响壁面辐射热流的一个重要因素.图7 还展示出,速度为6.74 km/s 时,辐射加热不明显,大约只有5 kW/m2,只占到对流加热的7%左右,考虑辐射效应后,对流加热几乎没有变化.随着马赫数的增大,激发的原子数目增多,壁面的辐射加热和对流加热的变化变得明显,速度为10.14 km/s 时,辐射加热占对流加热的30%左右,这与Bird[1]的结果一致,即飞行速度超过10 km/s 时,辐射加热变得明显.此外,选中的原子碰撞对碰撞后,部分相对平动能转化为原子的激发能,致使相对平动能减小,原子速度降低,当来流速度越大时,这种现象就越明显.因此,随着马赫数的增大,考虑辐射效应后,对对流加热的影响就越明显.可以从图7 中看出,当来流速度增加到10 km/s时,对流加热改变量为40 kW/m2左右,改变量是来流速度为6.47 km/s 改变量的(2.5 kW/m2左右)16 倍.

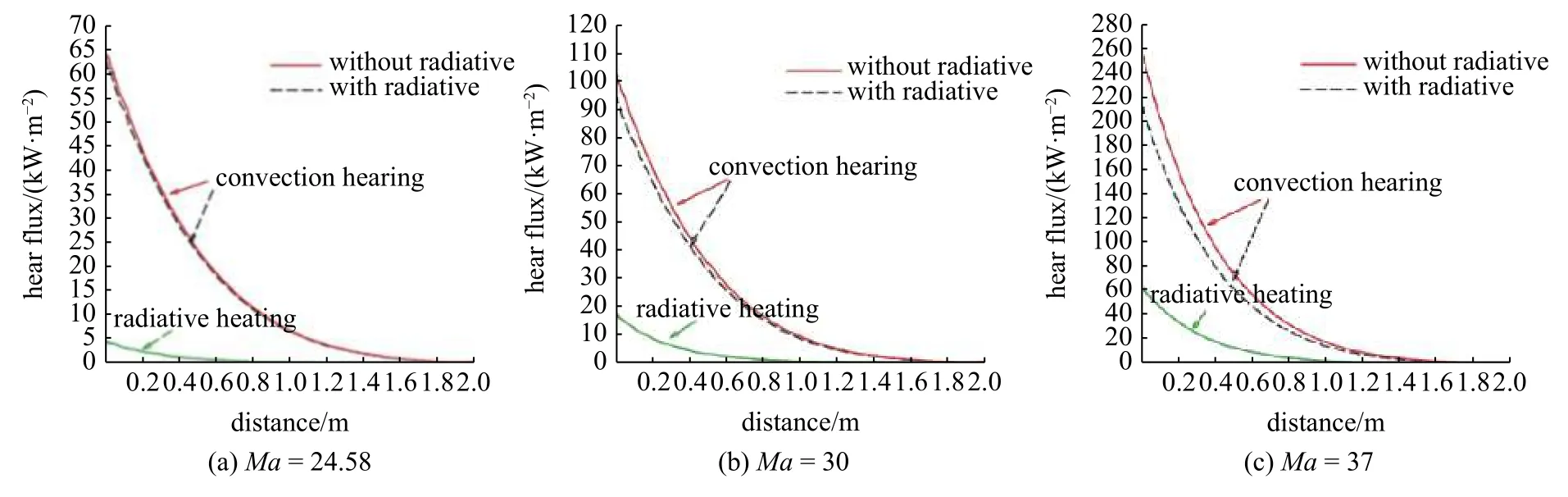
图7 原子辐射效应对壁面的辐射加热和对流加热Fig.7 Influence of atomic radiation effect on the radiative heating and convective heating on the wall

3 总结

基于以上的激发辐射模型和光子追踪技术,运用p-DSMC 方法,获得了超高声速二维圆柱绕流原子气体对壁面的辐射加热,从得到的数据中可以得出以下三条结论.

(1)来流速度低于10 km/s 时,辐射加热不明显,在驻点区域,辐射加热占对流加热比重在7%左右;来流速度大于10 km/s 时,在驻点区域,辐射加热占对流加热比重将超过30%.

(2)考虑了原子的辐射效应,对非平衡区的平动、转动和振动温度的最大值影响不大.

(3)在考虑了原子的辐射效应后,对于二维圆柱绕流,激波要更加贴体.

(4)流场中原子的浓度是影响壁面辐射热流大小的一个重要因素之一.

在本研究的基础上,将会持续开展高温空气组分的辐射效应建模研究,开发计算代码,并加强对比验证,为目标飞行器热防护系统提供可靠的热载荷数据.