O(t-β )-synchronization and asymptotic synchronization of delayed fractional order neural networks

Anbalagan PRATAP

Department of Mathematics，Alagappa University，Karaikudi 630004，India

E-mail: kapmaths gmail.com

Ramachandran RAJA

Ramanujan Centre for Higher Mathematics，Alagappa University，Karaikudi 630004，India

B-mail: rajarchm2012@gmail.com

Jinde CAO (曹进德)广

School of Mathematics，Southeast University，Nanjing 211189，ChinaYonsei Frontier Lab，Yonsei University，Seouul 03722，South Korea

E-mail : jdcao@seu.edu.cn

Chuangxia HUANG(黄创霞)*

Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering,Changsha University of Science and Technology，Changsha 410114，China

E-mail : cxiahauang@csust.edu.cn

Jehad ALZABUT

Department of Mathematics and General Sciences，Prince Sultan Uniuersity,Riadh 12435，Saudi Arabia

E-mail : jalzabut@psu.edu.sa

Ovidiu BAGDASAR

Department of Electronics，Computing and Mathematics,University of Derbg，United Kingdom

E-mail: ovidiubagdasargmail.com

1 Introduction

Over the past few years， many research areas such as control theory， stability theory，optimization， cryptography， secure communications， signal and image processing， have played a significant role in the study of neural networks and nonlinear dynamical systems [1–7]. The quantitative behavior of dynamical applications is an important step in the practical design[8–10]. Bidirectional associative memory (BAM)， an expansion of auto-associate Hopfield neural networks， was first proposed by Bart Kosko [11]， and contains twin layers， one a K-Layer and the other an L-layer. Between the two layers，the neurons are fully interconnected from K-layer to L-layer. This lays a good foundation for artificial intelligence，optimization，signal and image processing，and as such increasing attention has been paid to the dynamical behaviors of BAM neural networks， and some important results have been obtained; see [12–14].

Recently，research on fractional-order dynamical systems has brought about numerous fruitful achievements;see[15–17，48，49]. As an electronic execution of a BAM neural system model，many scholars endeavored to update the typical capacitor fractional capacitor; this led to the development of the fractional order BAM neural network models (FOBAMNNs). Generally，time delays can impose complexity and restrictions in neural networks and may lead to instability， chaos and oscillation. Dynamical behaviors of time delayed FOBAMNNs have already become a hot research topic，and lots of scientific results have appeared in this area;see[18–22].

For example， the non-fragile state estimator design of fractional order memristive BAM neural networks (FOMBAMNNs) with a parameter mismatch problem was investigated in[18]. By means of interval parameter techniques， nonsmooth analysis and Lyapunov theory，sufficient criteria were obtained in asymptotic stability for the considered BAM neural network models. In [19]， by employing the appropriate Lyapunov function and Caputo fractional derivatives， the author demonstrated the global Mittag-Leffler stability and asymptotical ωperiodicity of fractional order BAM neural networks (FOBAMNNs). Based on the properties of Riemann-Liouville fractional derivatives， the fractional Barbalet lemma and the Lyapunov stability theory， some sufficient conditions were established in [21] to guarantee the global asymptotic stability of FOBAMNNs with impulsive effects and time delays. In [22]， the problem on the stabilization of FOMBAMNNs was demonstrated. By utilizing the two different feedback control approaches， linear and partial feedback control， as well as the generalized Gronwall inequality and the properties of Caputo derivatives，the sufficient conditions were established to ensure the Mittag-Leffler stabilization condition for the considered FOMBAMNNs models.

Synchronization， which means the dynamical behaviors of a coupled system that realizes convergence to the matching spatial state， has become an important research field. Many interesting research topics in neural networks and complex networks have made great progress(see [23–26]). There are many applications of synchronization，for example，secure communication， medicine， image processing， and so on. For fractional-order neural networks， researchers have discussed various types of synchronization; see [27–33]. For example， in [28]， the author demonstrated several synchronization criteria by utilizing the suitable Lyapunov function， the Razumikhin method and the differential inclusion theory to ensure the O(t-β)-synchronization and adaptive Mittag-Leffler synchronization criterion in fractional order delayed memristive neural networks. In[30]，the authors proposed the problem of memristive fractional order fuzzy neural networks with time delays. By employing some inequality skills and a suitable state feedback control scheme， the set of sufficient conditions was presented to ensure the finite time stability and finite time synchronization. For more on the significant research taking place regarding fractional order synchronization in BAM neural networks， see [27， 31， 32] and references therein. In [31]， the problem of finite time Mittag-Leffler synchronization of memristive FBAMNNs was addressed with the aid of a simple linear feedback controller， some inequality techniques， and a suitable Lyapunov functional approach. The authors of [33] developed multiple variable delayed impulsive FBAMNNs by using linear delayed feedback control.

On the one hand， during a particular period， signal propagation is distributed because the variety of axon sizes and lengths are too large. The significant attention has been paid to distributed delays in neural network dynamical systems; see， for instance， [34， 35]. In [34]， the authors discussed the pinning synchronization of Riemann-Liouville sense fractional-order memristive complex-valued neural networks with both discrete and infinite distributed delays.By using the Lyapunov stability theory， a comparison theorem and a pinning control policy， several sufficient conditions were obtained to ensure the global asymptotical synchronization analysis of the considered neural network model. In[35]，by using the adaptive feedback control law and Lyapunov theory， the author investigated the global asymptotic synchronization of fractional order complex valued neural networks with both discrete and infinite distributed delays.

On the other hand， in many practical systems， many uncertain and external perturbations exist， which can damage synchronization’s dynamical performance. Taking account of this，many interesting results on the dynamics of neural networks with discrete， infinite distributed delays and nonlinear perturbations have recently been proposed; see [36–38]. These results are built in integer order cases. To the best of our knowledge， no one has yet investigated the fractional order cases， and in this paper， we make the first attempt to do so.

The main objective of this article is thus to study the O(t-β) synchronization and asymptotic synchronization for fractional order BAM neural networks with discrete delays，distributed delays and non-identical perturbations. The main contributions of this research work are follows:

1. The theoretical results and techniques can be extended to O(t-β) stability and the synchronization of both integer order and fractional-order neural networks.

2. To obtain our synchronization results， O(t-β) synchronization and asymptotic synchronization definitions have been introduced， and a novel discontinuous state feedback controller has been designed.

3. In light of these definitions and proposed controllers， sufficient criteria for several synchronization results are demonstrated theoretically.

4. While existing results have not taken into consideration nonlinear perturbation and mixed time delays， our results fill this gap.

2 Preliminaries

At first， let us present some standing definitions， and we also state four lemmas in this section.

Definition 2.1 ([39， 40]) The integral of fractional order β ＞0 for a function h(t) is defined as

3 Main Results

In this section， a new class of O(t-β)-synchronization and asymptotic synchronization are derived by employing a Mittag-Leffler function， a suitable Lyapunov functional， and fractional order derivative properties including the Riemann-Liouville and the Caputo-derivative.

We choose the controllers χi(t) and θj(t) in response system (2.2) as follows:

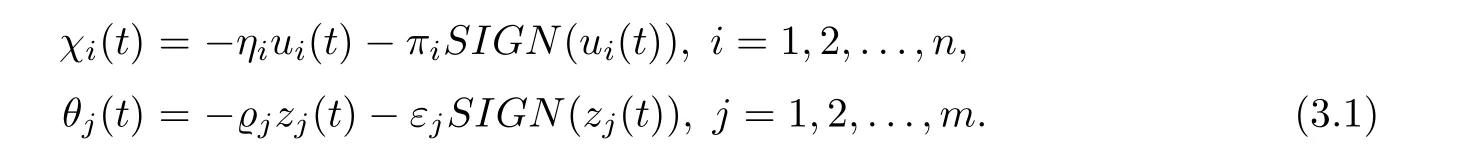
Here ηi， πi， ϱj， εjare control gains.

so the drive system(2.1)without infinite distributed delays realizes asymptotic-synchronization with response system (2.2) without infinite distributed delays under controller (3.1).

Corollary 3.6 Assuming that the conditions (A1)–(A2) hold， then there exist n positive constants δi(i = 1，2，...，n) and m positive constants γj(j = 1，2，...，m) such that the condition of (3.16) holds， so the drive system (2.1) without external disturbances realizes asymptotic-synchronization with response system(2.2)without external disturbance under controller (3.15).

Remark 3.7 This is the first time that O(t-β)-synchronization and asymptotic synchronization criterion for mixed time delayed BAM neural networks with a Caputo-fractional order have been investigated. In this work， fractional order， mixed time delays， nonlinear perturbations and a matrix element method have been taken into consideration; these results are very complicated and not easy to calculate. The main innovation of this paper is to extend and to overcome these complications. Our proposed model is more general and advanced.

Remark 3.8 In view of Theorem 3.1， the O(t-β)-synchronization implies asymptotic synchronization.

Remark 3.9 When β = 1， FBAMNNs model (2.1) degenerates into an asymptotic synchronization criterion for mixed time delayed BAM neural networks with nonlinear perturbation; these results do not exist in previous works.

Remark 3.10 In Theorems 3.1 and 3.4， the sufficient condition that guarantees the O(t-β)-synchronization and asymptotic synchronization criteria of mixed time delayed Caputo fractional order BAM neural networks with nonlinear perturbations are established in the forms of the matrix element method. These results can be easily evaluated without utilizing a MATLAB LMI control toolbox.

Remark 3.11 By using the results in FBAMNNs [31]， infinite distributed time delay and nonlinear perturbation terms are added to FBAMNNs， and these results are established by means of the Razumikhin method， a new class of Lyapunov method， a novel discontinuous controller and an asymptotic expansion of Mittag-Leffler function. Moreover， a few outcomes in [31] are special cases of our results obtained in Theorem 3.4 when infinite distributed time delay and nonlinear perturbation terms are not considered in acquiring system(2.1). Therefore，our proposed model is more general and advanced than [31].

4 Numerical Simulation

Here， two numerical cases are provided to check the advantages of our synchronization results from the previous section.

Therefore， all conditions of Theorem 3.1 hold. Hence system (2.1) realizes O(t-β) synchronization with system (2.2) under controller (3.1). The phase plots of state curves of the drive-response systems with control inputs are shown in Figure 1. Figure 2 depicts the time response of synchronization errors u1(t)， u2(t)，z1(t)and z2(t)of a system(4.2)that converges to zero， which confirms the effectiveness of O(t-β) synchronization results with the initial values k(t) = (0.6，-0.5)T， l(t) = (0.9，-0.5)Tand ˜k(t) = (0.4，1.9)T， ˜l(t) = (-1.2，0.5)T. By taking discrete delays， distributed delays and external disturbances into account， our main results rapidly lead to O(t-β)-synchronization for the above given parameters.

Figure 1 Phase plot of drive and response system with control inputs

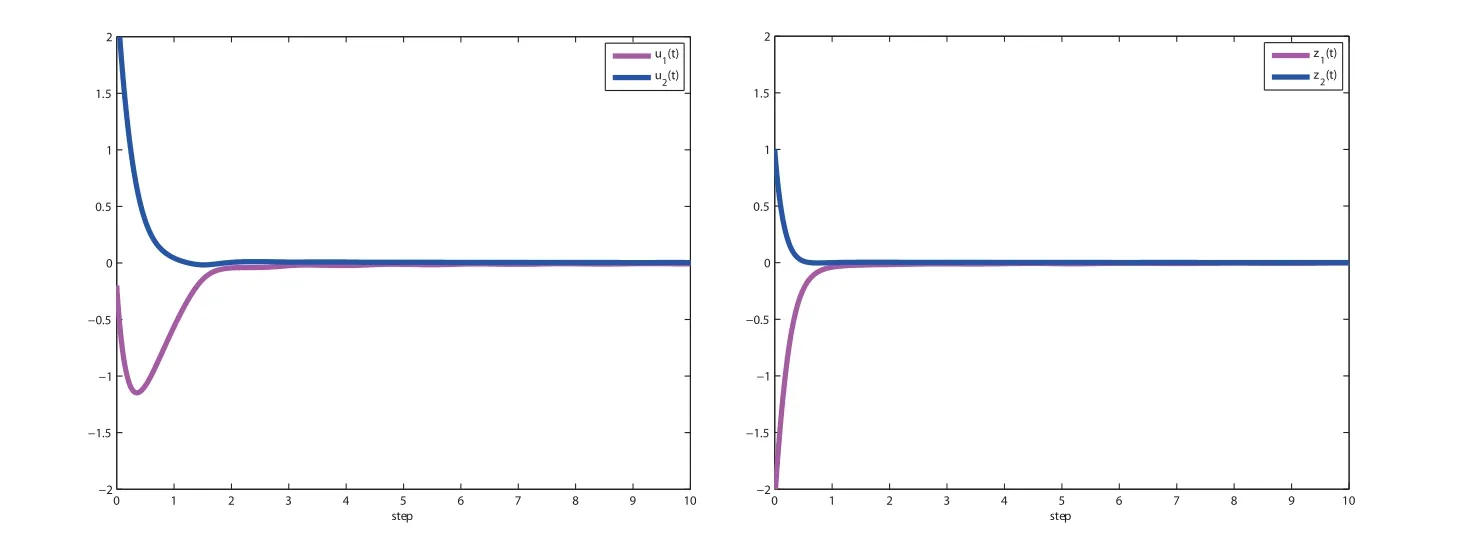
Figure 2 Synchronization error signal of drive and response system with control inputs

Figure 3 Chaotic behavior of drive and response system with control inputs

Figure 4 Synchronization error signal of drive and response system with control inputs

Therefore，the drive system(2.1)realizes asymptotic synchronization with response system(2.2)under controller(3.1)based on Theorem 3.4. The chaotic behavior of synchronization error curves of the drive-response systems with control inputs are shown in Figure 3. Figure 4 describes the time response of synchronization errors u1(t)，u2(t)，z1(t)and z2(t)of a system(4.2)that converges to zero， which confirms the effectiveness of asymptotic synchronization results with the initial values k(t) = (-1.2，1.5，2)T， l(t) = (-2，-4，2)Tand ˜k(t) = (-4，2.5，-3)T，˜l(t) = (0.5，1，1.5)T. By taking discrete delays， distributed delays and external disturbances into account， our main results rapidly lead to asymptotic synchronization for the above given parameters.

5 Conclusion

In this paper， several synchronization conditions of FBAMNNs with mixed time delays and nonlinear non-identical perturbations have been explored. By utilizing the proposed state feedback controller， fractional order derivative properties and a new kind of fractional order Lyapunov functional， we have demonstrated an algebraically sufficient condition for O(t-β)synchronization and the asymptotic synchronization of the considered FBAMNNs model. Two numerical examples have been given to show the effectiveness of our work.

Compared with O(t-β) synchronization and asymptotic synchronization， the convergence speed of finite-time synchronization is optimal and predictable. Furthermore， our system has other advantages， such as better robustness and interference suppression features. Therefore，it is important to investigate finite-time synchronization of neural networks. Some researchers proposed finite-time synchronization neural networks with both integer-order and fractional cases; for example， the authors of [45] investigated the finite-time synchronization of integerorder time-delayed coupled neural networks via intermittent quantized control. The authors of[46]studied the finite-time synchronization of integer-order time-delayed fuzzy neural networks via non-chattering quantized control. The authors of [47] derived the finite-time synchronization analysis of fractional-order memristor-based neural networks with different fractional-order cases 0 ＜α ＜1 and 1 ＜α ＜2. Motivated by the above mentioned references， the proposed analysis method can be extended to investigate some other dynamical behavior analyses such as finite-time passivity， finite-time dissipativity， finite-time stability， finite-time-stabilization，finite-time synchronization，and so on for fractional-order non-identical fuzzy BAM neural networks with time delays via intermittent quantized control; we will consider these interesting issues in future work.