Some further results for holomorphic maps on parabolic Riemann surfaces
Menglong HONG(洪梦龙)
School of Mathematical,East China Normal University,Shanghai 200000,China E-mail: 894326916@qq.com


appears. Dealing with this term is similar to dealing with the “error term” in the SMT.Therefore, to extend H. Cartan’s SMT, we need to use Ahlfors’ negative curvature method to get the precise terms.
2 Parabolic Riemann Surfaces
Parabolic Riemannian surface Y is a kind of Riemannian surface. Usually, we call a Riemannian surface with curvature 0 parabolic, and obviously, C is a parabolic Riemann surface.In addition, for any bounded subharmonic function f on the Riemann surface, if all of it is constant, Y must be Parabolic. From the paper [1], we know that Y is parabolic ⇔, and there is a smooth exhaustion function


holds, in a finite Lebesgue measure.

3 The First Main Theorem

4 Holomorphic Curves Into Pn(C)

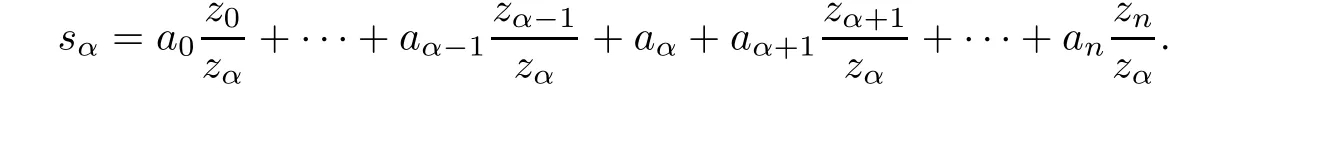

Before we prove Theorem 4.1, we recall some notations and some results. For the open set U ⊂Y, in the local coordinate U, write df =f′dz, z ∈U, and the higher order derivatives are



Let φk(H)=‖Fk;H‖2. By Lemma 4.6 and a calculation, we have Lemma 4.7.



5 Extension the Result of Ru
Nguyen Van Thin in[6]extended the results of Ru[2,3]to the maps of M-punctured disks,which is just a special case of Y. In this section, we extend the results of Nguyen Van Thin in[6] to Y.

be the m-th Hilbert weight defined on X about c.






6 Abelian Variety
In this section, we extend the result of Y.T. Siu and S.K. Yeung [4] to Abelian varieties,using A to represent an Abelian variety and letting dim(A) = n. From the definition of the derivative in [1], we also can define some global complex analytic 1-forms, for example {ωj:=dwj}0≤j≤n. This can help us find some global jet coordinates on JkA such that JkA=A×Ckn.Let ξ ∈Y be a fixed global vector. If f is holomorphic and from Y to A, we can define
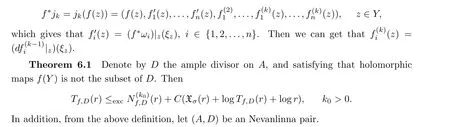

Proof of Theorem 6.1 On the first step, we consider the situation where f(Y) is not Zariski dense in Y. Take a Zariski closure X of f(Y). If X exists in another form by translating the Abelian subvariety of A,we can get mf(r,X∩D)=mf(r,D)on the premise that f(Y)/⊂D.In the above hypothesis, if X = A, then we also have X ∩D = D. It is contradictory. Let B = {a ∈A,a+X = X}, and the quotient group is defined as A/B = A0. In addition, we can instead of f by its synthesis of the quotient map A →A0. Without affecting the results,assume that X is not one of the translations of subgroup of A and that dim(X)>0.
Letting JkA=A×Rn,k, we recall that here Rn,kis the “universal”rational homogeneous variety Cnk/Gk(see line 2, page 2, Paun-Sibony [1]). Denote by Xkthe Zariski closure on fk(Y), and meanwhile use the injection Xk→Akto synthesize the map τk: Xk→Rn,k,which located in the second factor JkA →A×Rn,k. By the Prop-5.3 in [1], ∀1 <k, when the dimension of the fiber of τkis greater than zero, dim(AX) is strictly positive, where AXis defined as
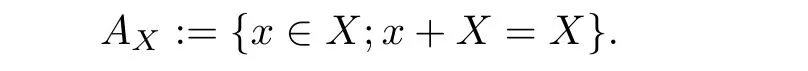
In addition, from the above assumption, we know that τkhas finite generic fibers, where τkis a mapping from Xkto Rn,kand k is greater than or equal to one. Thus, from Prop-5.4 of Paun-Sibony [1], we can find an order k jet-differential P such that its values in the dual of an ample line bundle and its restriction to Xkare not identical to 0. By Theorem 3.2 (b) in [15],this implies that (take D with empty)



Acknowledgements Thanks to my advisor Min Ru and Xuecheng Pang for their help.
 Acta Mathematica Scientia(English Series)2022年4期
Acta Mathematica Scientia(English Series)2022年4期
- Acta Mathematica Scientia(English Series)的其它文章
- ITERATIVE ALGORITHMS FOR SYSTEM OF VARIATIONAL INCLUSIONS IN HADAMARD MANIFOLDS*
- Time analyticity for the heat equation on gradient shrinking Ricci solitons
- The metric generalized inverse and its single-value selection in the pricing of contingent claims in an incomplete financial market
- The global combined quasi-neutral and zero-electron-mass limit of non-isentropic Euler-Poisson systems
- Global well-posedness of the 2D Boussinesq equations with partial dissipation
- A uniqueness theorem for holomorphic mappings in the disk sharing totally geodesic hypersurfaces
