Time analyticity for the heat equation on gradient shrinking Ricci solitons
.Jiayong WU (吴加勇)
Department of Mathematics,Shanghai University,Shanghai 200444,China E-mail: wujiayong@shu.edu.cn

Recall that an n-dimensional Riemannian manifold (M,g) is called a gradient shrinking Ricci soliton (M,g,f) (also called a shrinker for short) (see [10]) if there exists a smooth potential function f on M such that

where A3is some constant depending only on n and A2, and 00=1. Here µ=µ(g,1) denotes Perelman’s entropy functional.
Remark 1.2 The growth condition is necessary. As in [3], let v(x,t) be Tychonov’s solution of the heat equation in (Rn,δij,|x|2/4)×R such that v =0 if t ≤0 and v is nontrivial for t >0. Then u := v(x,t+1) is a nontrivial ancient solution of the heat equation and is not analytic in time. Note that |u(x,t)| grows faster than ec|x|2for any c >0, but for any∈>0, |u(x,t)| is bounded by c1ec2|x|2+∈for some constants c1and c2. This implies that growth condition (1.4) is sharp.
In general, the Cauchy problem to the backward heat equation is not solvable. However,on a complete non-compact shrinker, we can obtain a solvable result by a simple application of Theorem 1.1.
Corollary 1.3 Let(M,g,f)be an n-dimensional complete non-compact gradient shrinking Ricci soliton satisfying (1.1), (1.2)and (1.3). For a fixed point p ∈M, the Cauchy problem for the backward heat equation
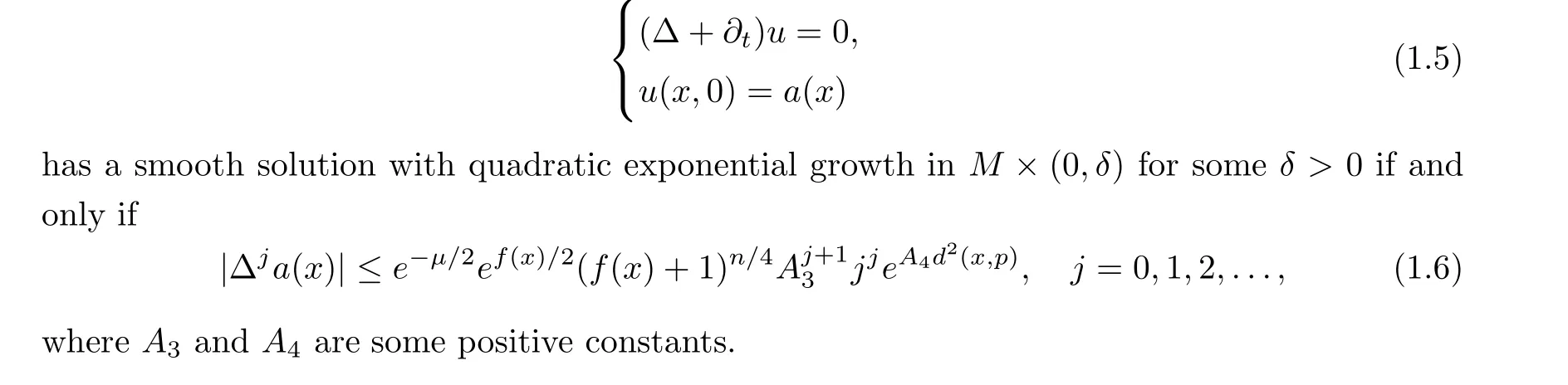
The rest of this paper is organized as follows: in Section 2, we recall some properties of gradient shrinking Ricci solitons. In particular, we give a local mean value type inequality on gradient shrinking Ricci solitons. In Section 3, adapting Dong-Zhang’s proof strategy [3], we apply the mean value type inequality of Section 2 to prove Theorem 1.1 and Corollary 1.3.
2 Some Properties of Shrinkers
In this section, we will present some basic propositions about complete non-compact gradient shrinking Ricci solitons; these will be used in the proofs of our main results.
On an n-dimensional complete non-compact gradient shrinking Ricci soliton(M,g,f)satisfying (1.1), (1.2)and(1.3), from Chen’s work(Proposition 2.2 in[16]),we know that the scalar curvature is R ≥0. Moreover, by [17], we know that the scalar curvature R must be strictly positive, unless (M,g,f) is the Gaussian shrinking Ricci soliton (Rn,δij,|x|2/4).

For any fixed point p ∈M, by Theorem 1.1 of Cao-Zhou [18] (later refined by Chow et al.[19]), we have on (M,g,f). It remains an interesting open question as to whether or not the scalar curvature R is bounded from above by a uniform constant.
By Cao-Zhou [18] and Munteanu [20], the volume growth of a gradient shrinking Ricci soliton can be regarded as an analogue of Bishop’s theorem for manifolds with non-negative Ricci curvature (see [21]). That is, there exists a constant c(n) depending only on n such that

The point(p,s)and the radius r in Proposition 2.2 is customarily called the vertex and the size of parabolic cylinder Qr(p,s), respectively. Compared with the classical mean value type inequality of manifolds, there seems to be a lack of a volume factor Vp(r) in (2.4). However if the factor rnis regarded as Vp(r), this inequality is very similar to the classical case.

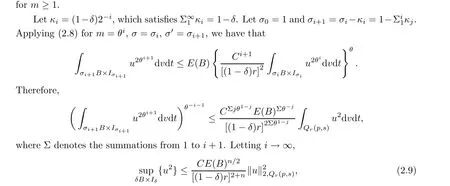
which clearly implies (2.4) when m=2, since Iδ2⊂Iδ.
The case m >2 then follows by the case m = 2, because if u is a nonnegative solution of(Δ-∂t)v ≥0, then um, m ≥1, is also a nonnegative solution of (Δ-∂t)v ≥0. All in all, we do, in fact, prove (2.4) when m ≥2.
When 0 <m <2, we will apply (2.9) to prove (2.4) by a different iterative argument. Let σ ∈(0,1) and ρ=σ+(1-σ)/4. Then (2.9) implies that

3 Proof of Results
In this section, adapting the argument of Dong-Zhang [3], we will apply the preceding propositions of shrinkers in Section 2 to prove Theorem 1.1 and Corollary 1.3. We first prove Theorem 1.1.
Proof of Theorem 1.1 Without loss of generality,we may assume that A1=1,because the heat equation is linear. To prove the theorem,it suffices to confirm the result at space-time point (x,0) for any x ∈M.
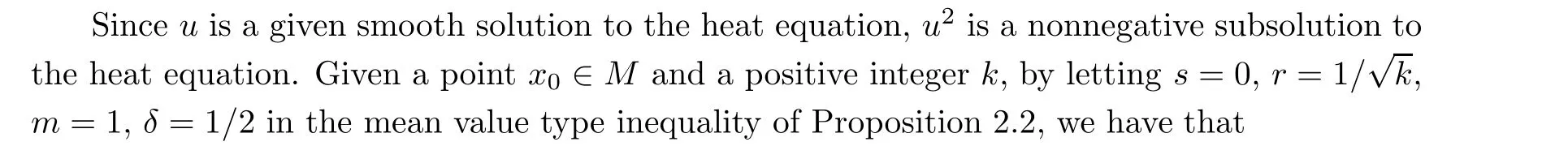


where both series converge uniformly for (x,t) ∈Bp(R)×[-δ,0] for any fixed R >0. Since u(x,t) is a solution of the heat equation, this implies that
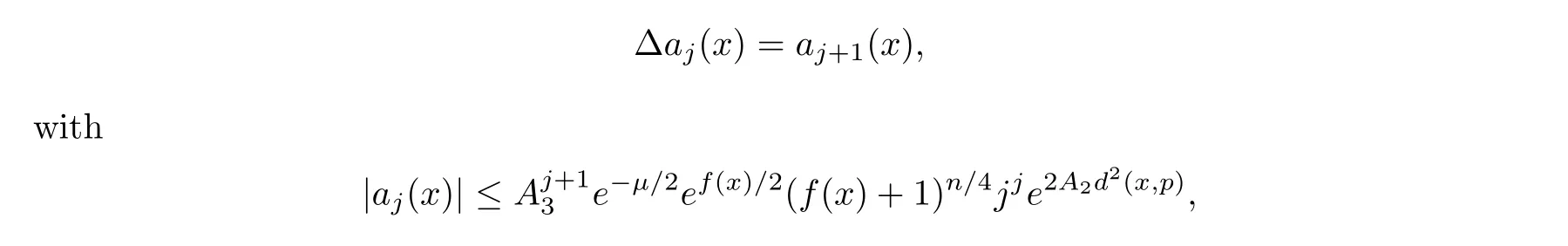
where A3is a positive constant depending only on n and A2. □
In the end, we apply Theorem 1.1 to prove Corollary 1.3.
Proof of Corollary 1.3 Assume that u(x,t)is a smooth solution to the Cauchy problem of the backward heat equation (1.5) with quadratic exponential growth. Then u(x,-t) is also a smooth solution of the heat equation with quadratic exponential growth. By Theorem 1.1,we have that

Acknowledgements The author sincerely thanks Professor Qi S. Zhang for helpful discussion about the work [3].
 Acta Mathematica Scientia(English Series)2022年4期
Acta Mathematica Scientia(English Series)2022年4期
- Acta Mathematica Scientia(English Series)的其它文章
- ITERATIVE ALGORITHMS FOR SYSTEM OF VARIATIONAL INCLUSIONS IN HADAMARD MANIFOLDS*
- The metric generalized inverse and its single-value selection in the pricing of contingent claims in an incomplete financial market
- The global combined quasi-neutral and zero-electron-mass limit of non-isentropic Euler-Poisson systems
- Some further results for holomorphic maps on parabolic Riemann surfaces
- Global well-posedness of the 2D Boussinesq equations with partial dissipation
- A uniqueness theorem for holomorphic mappings in the disk sharing totally geodesic hypersurfaces
