边界传热条件下甲烷水合物降压分解的LBM模拟

张 华，梁海峰，邵伟强，张锡彦

（太原理工大学 化学工程与技术学院，山西 太原 030024）

水合物是由水分子组成的笼状晶体，包裹一个或多个客体分子[1]。天然气水合物也称甲烷水合物，储量巨大、燃烧清洁，对于解决全球能源和环境问题具有战略意义，对其开采已成为国内外研究热点。水合物开采方法包括降压法、注热法、注化学剂法和二氧化碳置换法等[2-4]，其中降压法、注热法是相对实用的开采方式。

甲烷水合物储存地质条件复杂，目前主要是通过实验和数值模拟等方式开展研究。YOUSIF等[5]通过实验研究了多孔介质中水合物的分解特性，分析了渗透率和孔隙率对水合物分解过程的影响。宋永臣等[6]模拟了天然气水合物在降压和边界传热条件下的分解过程，对不同位置处压力、温度和产气率等的变化进行了研究。DAI等[7]建立了水合物沉积物在不同孔隙结构和赋存状态下的渗透率变化模型。WANG等[8-10]建立了减压、注热和减压联合注热的解析模型，发现降压与注热联合开采能够有效地提高水合物的分解速率。WANG等[11]利用微流体装置研究了孔隙中甲烷水合物的形成和分解，并且在形成过程中观察到稳定和不稳定的水合物晶体。

上述研究均采用宏观数值模拟方法，不能体现多孔介质孔隙结构及水合物赋存方式的影响。格子Boltzmann（LBM）方法从介观角度出发，可以直接简单地处理流体的流动过程及流体与周围环境之间的相互作用。LBM方法首先运用于水合物渗透率研究的模拟中。YU等[12]采用LBM方法研究了水合物存在对多孔介质渗透率的影响。喻西崇等[13]和JI等[14-15]采用LBM方法研究了不同饱和度水合物单相流和多相流的渗透率。HOU等[16]基于LBM方法研究了矿物颗粒和水合物孔隙尺度分布等因素对渗透率的影响，并提出了“控制渗流通道”的概念。DONG等[17]结合有限元和LBM方法模拟了水合物在岩石中的不同胶结方式，发现胶结方式对岩石的电阻率、弹性模量和渗透率有一定影响。

近年来LBM方法逐步被运用于水合物分解过程的模拟。ZHANG等[18]基于LBM方法描述了甲烷水合物分解的相变和不同孔隙下的孔隙结构演化，并对裂解锋的推进和温度分布进行了一些研究。吉梦霞等[19]和苗旭[20]基于LBM方法研究水合物分解特性，并将分解过程看作恒温。YANG等[21-22]基于LBM方法建立了水合物分解孔隙尺度的数学模型，研究了多孔介质中甲烷水合物解离过程的影响因素，分析了传质传热和水饱和度对甲烷水合物解离过程的影响。综上，LBM方法运用于水合物分解过程的模拟较少，且大多未考虑分解过程中的传热，以及水合物分解的固相消融影响。

本文基于LBM方法，建立描述甲烷水合物分解的动力学模型、流体流动模型以及传质和传热模型，运用固相更新（VOP）法追踪水合物固相变化，研究了不同边界条件（加热和绝热）、不同影响因素（边界温度、孔隙率和赋存状态）下，水合物的传热机理和产气特性。

1 模型与模拟

1.1 甲烷水合物分解的动力学模型

Kim-Bishnoi水合物分解动力学模型被广泛应用于多孔介质水合沉积物的模拟[23]，该模型水合物分解的驱动力为三相反应的平衡逸度fed与局部气体的逸度f之差。水合物产气率表示如下：

式中，nt为甲烷物质的量，mol；t为反应时间，s；As为水合物反应表面积，m2；kd为水合物反应动力学速率，mol/(m2·Pa·s)。

式中，k0为固有反应动力学常数，1.25×105mol/(m2·Pa·s)；ΔEa/R为9752.73 K；ΔEa为反应活化能，J/mol；R为摩尔气体常数，8.314 J/(mol·K)；T为反应温度，K。

一般情况下，式(1)中平衡逸度fed和局部气体的逸度f用相应温度T的平衡压力pe和甲烷气体压力p代替（单位为Pa），表示如下：

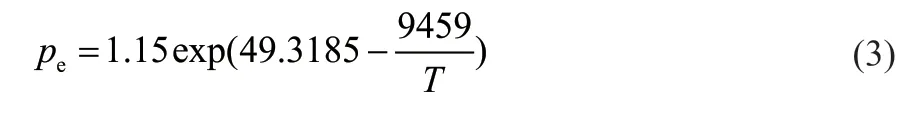
1.2 基于LBM的甲烷水合物分解模型

1.2.1 流体流动模型

在本研究中，因为水合物分解过程会产生水和甲烷气体，故采用ZHAO等[24]在Shan-Chen模型基础上改进的气液两相流流动大密度比伪势模型，引入新的势函数来表示气液两相间的相互作用力。各组分的密度分布函数表示如下：

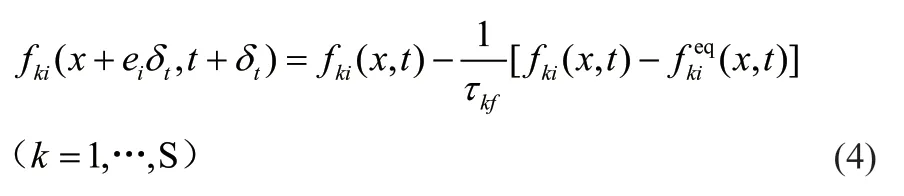
式中，fki(x,t)为某组分k在位置x和时间t下第i个速度方向上的密度场分布函数；t为反应时间，s；δt为时间步长；为平衡分布函数；ei为粒子的离散速度；τkf是粒子的无量纲弛豫时间。

在本研究中流体流动采用二维的D2Q9，空间上9个速度方向的离散速度ei表示如下：

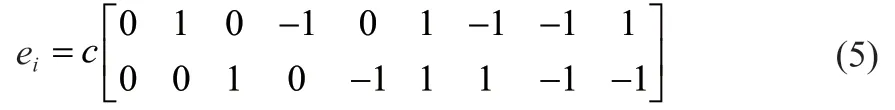
式中，c为晶格速度，c=δx/δt，δx为晶格间距。

D2Q9平衡分布函数表示如下：

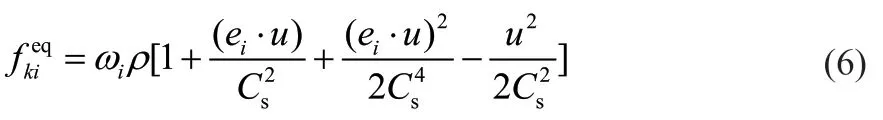
式中，ρ为组分密度，kg/m3；权系数ω0=4/9，ω1～4=1/9和ω5～8=1/36；格子声速。流体密度ρ和流速u的关系如下：

为了解决伪势模型中气液两相大密度比带来的不稳定问题，两组件的相互作用势可表示如下：

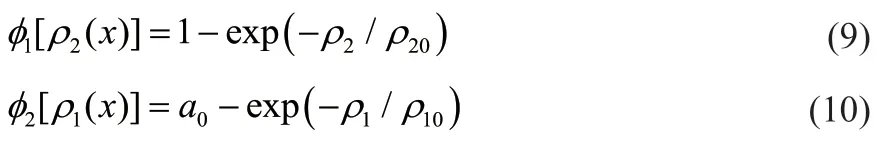
式中，φ1为气体的相互作用势；φ2为液体的相互作用势；0＜a0＜1，本研究中a0=0.005；ρ10=-0.0008/log(a0)；ρ20=0.0003。

新的总相互作用势如下：

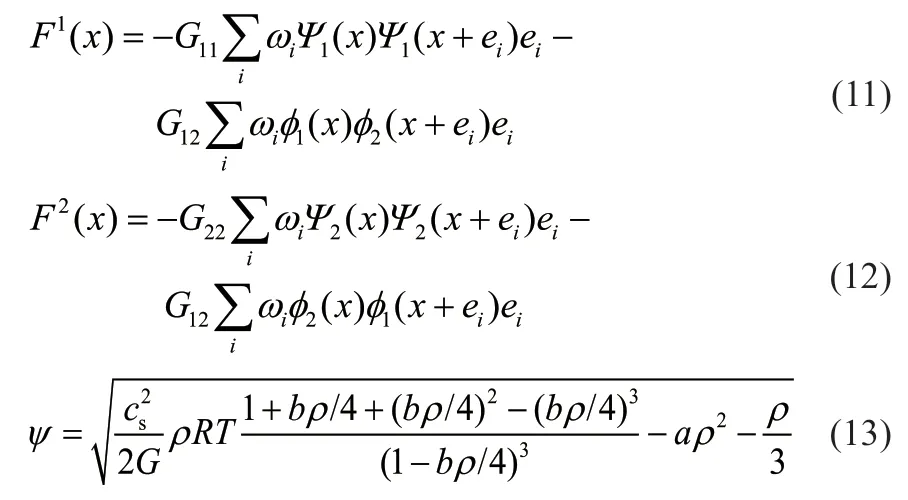
式中，G为组分间的相互作用力，N；ψ为势函数；a和b为参数，分别取值1和2。

1.2.2 传质模型

传质方程中浓度分布函数表示如下：

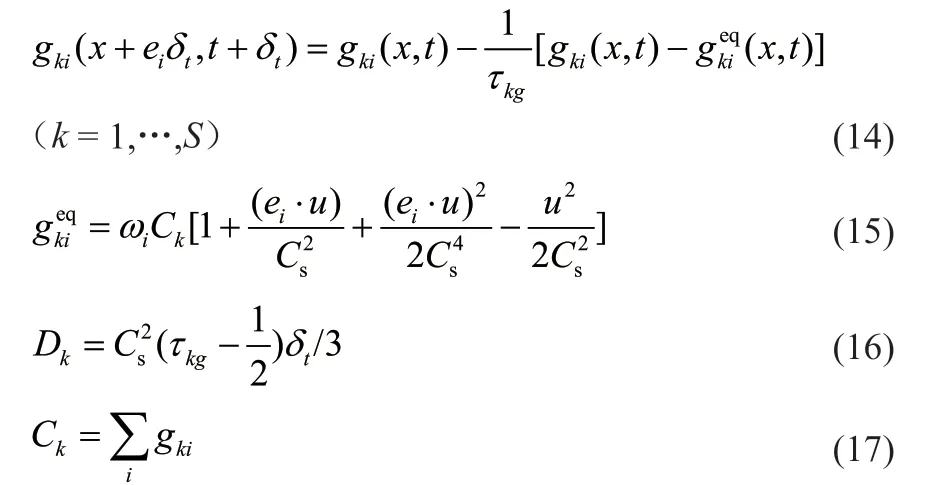
式中，gki为组分k的浓度分布函数；为组分k的平衡浓度分布函数；τkg为浓度场组分k的无量纲弛豫时间；Dk为扩散系数；Ck为组分浓度，mol/L。

1.2.3 传热模型

甲烷水合物分解的同时会不断吸收热量。本研究采用KARANI等[25]提出的附加源项方法，处理具有多个演化和移动界面的甲烷水合物分解过程中的耦合传热。

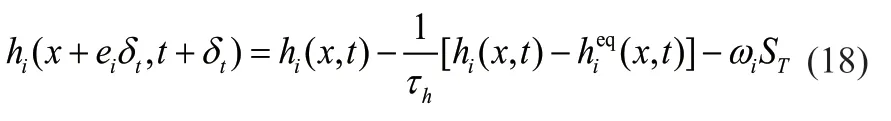
式中，hi为某时间段的温度分布函数；为平衡温度函数；τh为温度场的无量纲弛豫时间；ST为源相，K。

传热的D2Q5模型能够准确地恢复到宏观方程且能提高计算效率，简化的D2Q5晶格模型是通过放弃原始D2Q9模型对角方向（i=5～8）的离散速度而得到的，平衡的温度函数表示如下：

温度场的热扩散系数和宏观温度由以下确定：

在流体与水合物固体界面处，水合物逐渐被分解，周围的热量被吸收，而在其他的地方没有分解，所以源相ST=0，ST的表达式如下：

计算水合物分解吸收的热量采用MASUDA等[26]所给出的表达式：

式中，mH为水合物产气率，g/s；MH为水合物的摩尔质量，g/mol；参数r=56599 J/mol；参数d=16.744 J/(mol·K)。

1.2.4 边界条件

在水合物液固界面处发生非均相反应，把水合物分解看成一级反应，参照文献[27]中可以得出分解速率为：

式中，υ为气体黏度，m2/s；G为甲烷密度，kg/m3；n为沿边界的法相向量；M为水合物分解产生气体的摩尔质量，g/mol。

ZHANG等[28]提出了一种LBM浓度边界的一般回弹格式，浓度边界条件和浓度梯度计算如下：

式中，CR为边界点处的浓度，mol/L；CF为相邻点流体点的浓度，mol/L；|Δx|为两点间距离，m。

分解界面处的浓度计算如下：

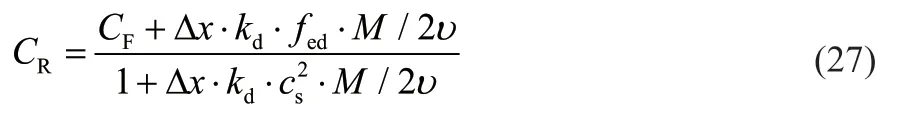
确定边界浓度后，根据ZHANG等[28]的反弹公式，可以确定边界条件的分布函数为：

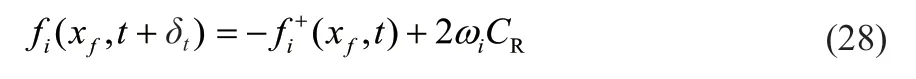
1.2.5 水合物分解固相更新法

模拟甲烷水合物分解的过程中，KANG等[29]采用开发的VOP法来不断地更新甲烷固体水合物的体积变化。VOP法是一种前沿跟踪方法，可用于跟踪不断演化的固液界面，广泛应用于反应输运问题。本研究中，只有流体与水合物分解界面处的固体水合物需要进行处理。将每个节点表示为一个控制体积，水合物节点的体积通过以下公式计算：

式中，As为表面反应面积，m2；为摩尔体积，m3/mol ；V为水合物体积，m3。

水合物体积根据每一个时间步长进行更新：

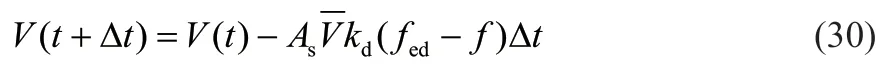
1.2.6 模拟实现过程

模拟甲烷水合物的分解过程，主要步骤如下：

（1）将单位无量纲化，初始化计算区域；

（2）基于Kim-Bishnoi模型，构建水合物分解的LBM流体流动、传质和传热模型；

（3）更新水合物结构并计算相关信息；

（4）不断重复步骤（2）、（3）直至水合物完全分解。

基于LBM法进行水合物分解过程，分解、流动、传质和传热机理的研究。建立多孔介质模型，该模型计算的物理尺寸为0.22 m×0.10 m，采用220×100的格子单位，每一个圆形颗粒半径为8（格子单位），如图1所示。

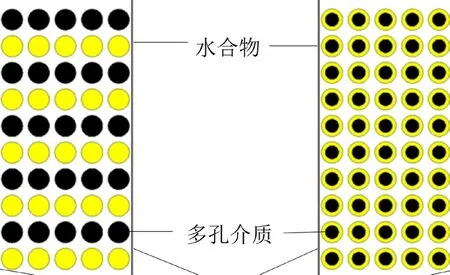
图1 多孔介质的孔隙结构Fig.1 Pore structure of porous media

孔隙率是模拟多孔介质沉积物的重要因素之一，对于图1中排列的多孔介质模型，孔隙率计算式如下：

式中，ε为圆的直径DP与圆心距D的比值。

2 模拟结果与讨论

2.1 不同边界传热方式对甲烷水合物分解的影响

图2和图3分别为悬浮状态下边界温度为280.3 K和边界绝热下的温度云图。由图2可知，当边界加热时，边界处和开口处的水合物由于受到边界温度和开口压力的影响，率先分解完成，然后向中心推进。边界的热量也随着分解的进行逐渐向中心传递，当水合物完全分解，边界的温度并没有均匀分布，边界的传热范围十分有限。由图3可知，当边界绝热时，温度一直降低，直到水合物停止分解；受甲烷和水向出口处流动的影响，开口处的温度较高。

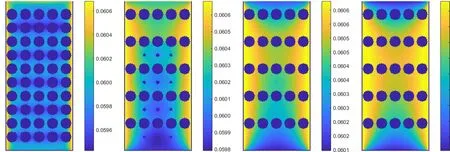
图2 边界温度280.3 K下的温度云图Fig.2 Temperature cloud diagram with boundary temperature 280.3 K

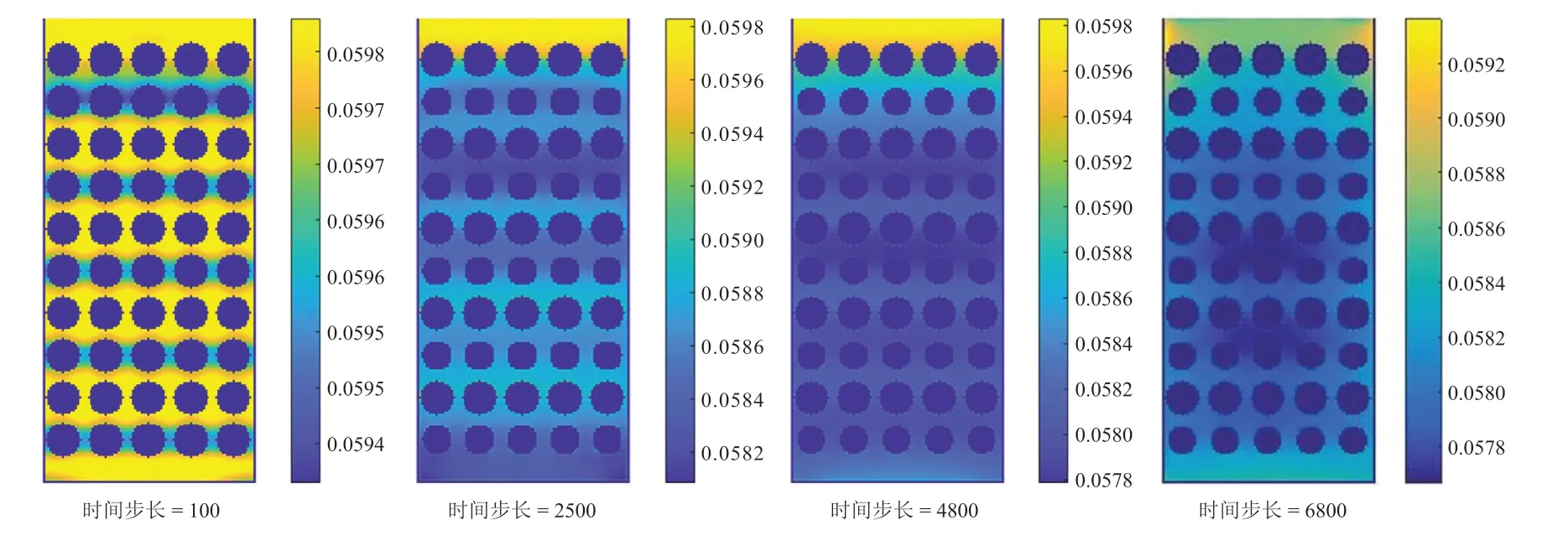
图3 边界绝热下的温度云图Fig.3 Temperature cloud diagram with boundary adiabatic

2.2 不同边界温度对甲烷水合物分解的影响

甲烷水合物分解是吸热反应，因此边界传热对其有一定影响。图4给出了悬浮状态下不同边界温度对水合物分解的影响。由图4(a)可知，不同边界温度下，水合物分解前期的累计产气量和产气率变化趋势接近，说明前期主要由压力控制，边界温度的影响很小；随着温度的传递，边界处温度高分解完成的时间较短，且完全分解的累计产气量为4925 cm3；但随着边界温度增高，其对水合物分解的影响不断减小。而边界绝热时，累计产气量为1832.8 cm3，仅为完全分解时的3/8，因此在水合物降压分解过程中需要通入充足热量，以便水合物可以完全分解。由图4(b)可知，当边界加热时，温度短暂上升，由于水合物分解吸收热量大于边界提供的热量，温度开始下降，随着边界加热的不断进行，温度又上升到边界温度。而边界绝热时，外界不能提供热量，平均温度下降到273.2 K左右后不再下降，因此在水合物开采过程中需要考虑水结冰和水合物再生成的情况。

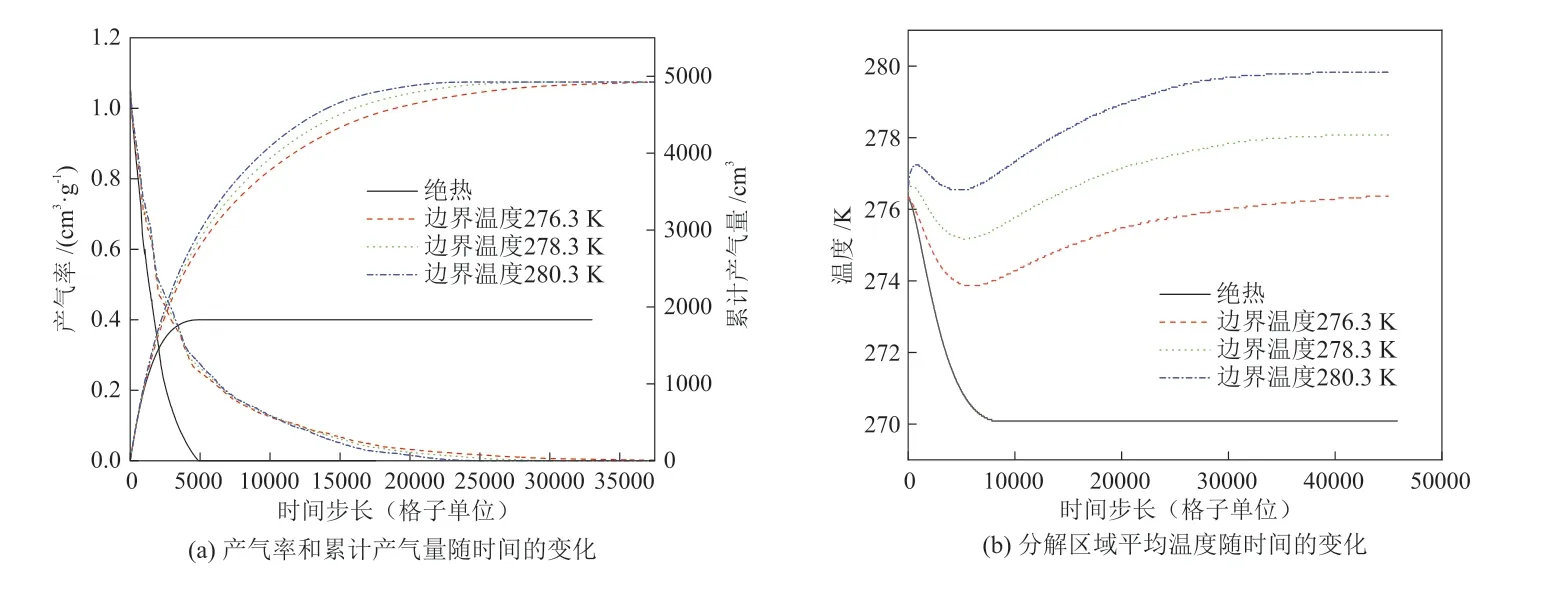
图4 不同边界温度对甲烷水合物分解的影响Fig.4 Effect of different boundary temperatures on decomposition of methane hydrate

2.3 不同孔隙率对甲烷水合物分解的影响

孔隙率是模拟多孔介质沉积物的重要因素之一，反映了甲烷水合物饱和度和多孔介质形态。模拟了边界温度278.3 K和边界绝热条件下，0.37、0.45和0.53这3种孔隙率对水合物分解的影响。由图5(a)可知，当边界传热时，孔隙率较大产气率下降速度较快，水合物分解完成时间较短，说明孔隙率较大有利于流体流动和热量传递，促进了水合物分解。反应在时间步长11000步之前，孔隙率较大的产气率也大，然而随着反应的进行，孔隙率较大的产气率反而变小，这是由于孔隙率较大的产气量较大，反应表面积减小。而边界绝热时，由于热量的影响，水合物较早停止分解，产气率和累计产气量变化趋势几乎一致，可以忽略孔隙率对水合物分解的影响。由图5(b)可知，随着孔隙率的增大，初始温度下降的越快，最低点温度也越低，达到最低点温度的时间也不断地提前，之后快速上升到边界温度。

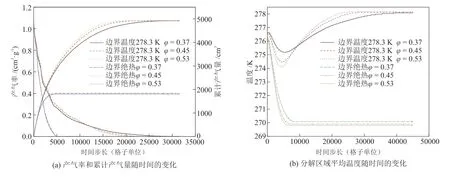
图5 不同孔隙率对甲烷水合物分解的影响Fig.5 Effect of different porosity on decomposition of methane hydrate

2.4 不同赋存方式对甲烷水合物分解的影响

甲烷水合物的赋存方式反映了水合物在地层中与周围多孔介质的相互关系，不同的赋存方式影响着水合物的基本特性。水合物在多孔介质中的主要赋存形式可以分为两种：悬浮和包裹（图1）。本节模拟了悬浮和包裹两种水合物赋存状态下，边界温度278.3 K和绝热边界条件下的情况。由图6(a) 可知，绝热边界条件下，包裹状态累计产气量为4126.9 cm3，悬浮状态累计产气量为1832.8 cm3，分别是完全分解总量的5/6和3/8，可见包裹状态有利于提高水合物的产气量。由图6(b)可知，悬浮和包裹状态下降的温度接近，表明包裹状态水合物更多是由压力控制分解的。边界加热时，包裹状态下的分解速率较快，但温度的下降和上升也十分迅速，而且最低温度下降到273.2 K左右。故在包裹状态下开采时，应注意温度影响。在边界加热条件下，由于表面积的影响，包裹状态水合物在时间步长3060步内分解完全；而悬浮状态水合物在时间步长30240步内分解完全，远远大于包裹状态。

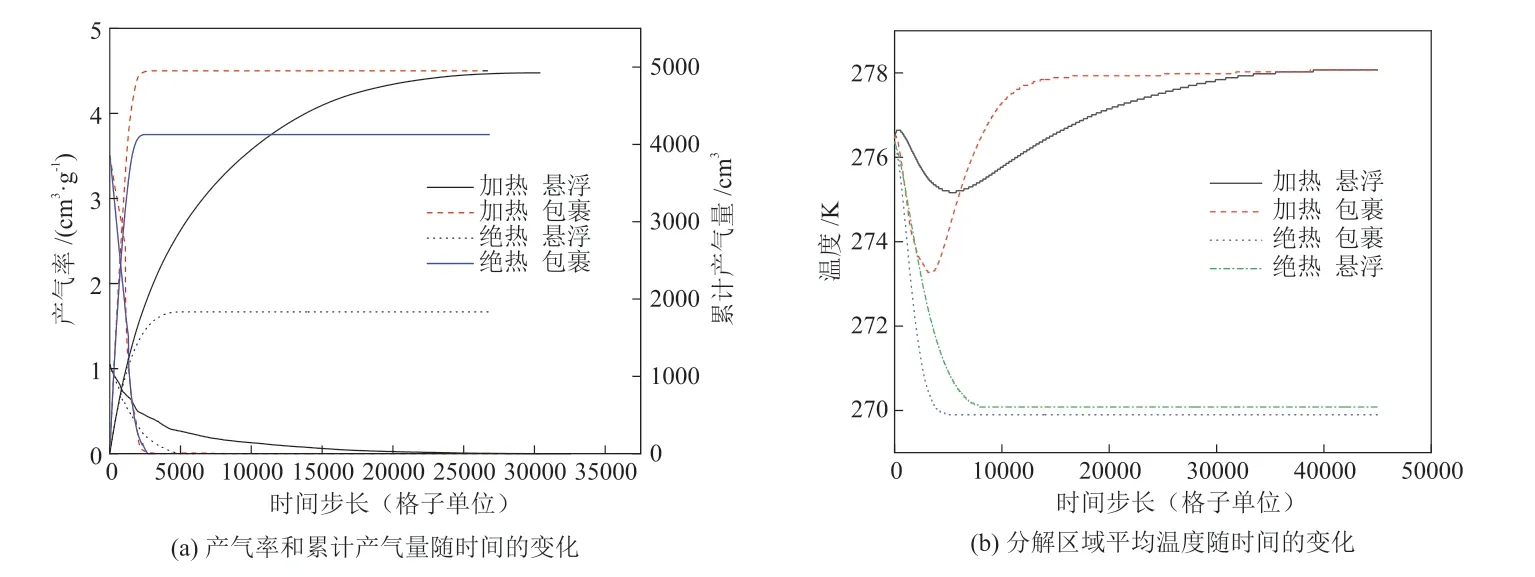
图6 不同赋存方式对甲烷水合物分解的影响Fig.6 Effect of different occurrence modes on decomposition of methane hydrate

3 结论

基于LBM方法，建立了水合物分解的Kim-Bishnoi动力学模型，流体流动、传热和传质模型。从边界绝热、边界加热两个方面研究了不同影响因素下甲烷水合物的传热机理和产气特性，得到以下结论。

（1）边界加热和边界绝热下水合物分解的累计产气量分别为4925.0 cm3和1832.8 cm3，边界加热有利于提高水合物的分解速率和产气量。随着边界温度的增加，水合物完成分解所用时间变化并不明显。

（2）孔隙率较大有助于流体流动，从而加快边界温度的传递。而绝热条件下，受温度的影响，孔隙率对水合物影响较小。开采过程中，孔隙率较大时，需要同时考虑降压和加热开采。

（3）绝热条件下，包裹状态水合物累计产气量为4126.9 cm3，悬浮状态累计产气量为1832.8 cm3，分别是完全分解总量的5/6和3/8。包裹状态不仅可以缩短开采时间，还可以提高产气量。