基于改进型MPC策略的BLDCM转矩脉动抑制*
白国长,马超群,娄 轲
(郑州大学机械与动力工程学院,郑州 450001)
0 引言
无刷直流电机(brushless DC motor)因为结构简单、功率密度大等优点使其在日常生活和工业生产中得到广泛应用[1-2]。由于本身结构、控制方式等原因,BLDC在工作运行时会产生转矩脉动,会导致电机全速工作时的抖动,产生转速不平稳,影响工作精度,严重抑制BLDC在高精度场合的应用。其中由换相过程中产生的换相转矩脉动可能达到平均转矩的50%。因此研究BLDC换相转矩脉动的抑制方法一直是热点[3-10]。
LIU等[11]通过提出构造转矩平衡点观测器的最优控制算法,实现了低速运行阶段无刷直流电机换相转矩脉动的抑制。龚文倩等[12]通过对直流路电压进行调整和增加SEPIC斩波电路来使直流侧电压和反电动势保持正比关系,进而降低转矩脉动。王晓远等[13]将电流预测控制与PWM_ON法相结合,分别计算出开通相和关断相的占空比,对电流进行控制,来减小电机换相转矩脉动。李奥等[14]提出一种基于Buck变换器的无刷直流电机四闭环控制方法,对电机转速、相电流、Buck变换器输出电压以及电感电流进行闭环控制,进而降低了换相转矩脉动。白国长等[15]提出了一种准Z源网络三相四开关逆变器的容错方法,从而抑制无刷直流电机驱动故障容错切换后的转矩脉动。
本文对换相转矩脉动原理进行分析,提出了一种控制非换相相电流的改进型模型预测控制(MPC)策略。通过该策略预测非换相相电流和电磁转矩值,使用代价函数(cost function)最小化上述预测参数的误差平方,并基于最小代价推导出开关管的最佳切换状态,保持非换相相电流的恒定,以此来实现换相转矩脉动的抑制。在两相导通阶段使用了传统PID控制策略进行控制,所提出的基于改进型MPC的控制策略应用于换相阶段。最后通过仿真以及实验验证了该策略的有效性。
1 BLDCM数学模型
无刷直流电机常常采用两相导通方式,理想状态下得到电压平衡方程为:
(1)
无刷直流电机系统等效电路图如图1所示。
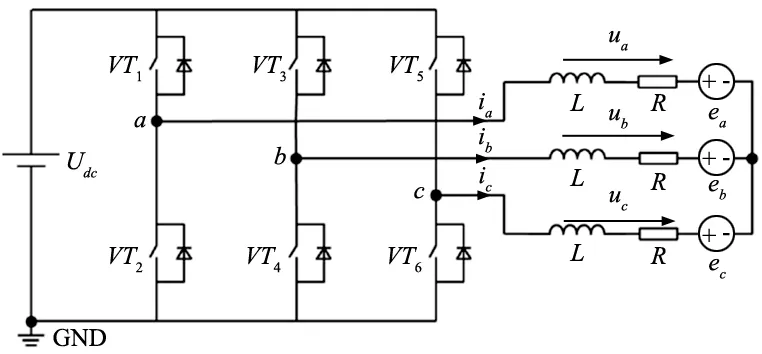
图1 BLDCM系统等效电路图
图中,R、L为定子绕组的相电阻和等效相电感;ia、ib、ic为三相相电流;ea、eb、ec为三相相反电动势;ua、ub、uc为端电压;uN为中性点电压。理想状态下的电机反电动势、相电流和霍尔信号如图2所示。
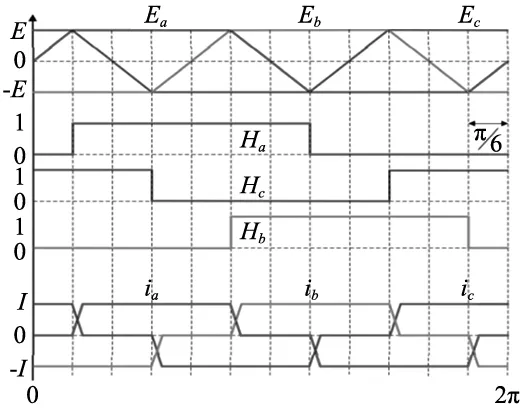
图2 理想状态下的电机反电动势、相电流和霍尔信号
由图(2),BLDCM的电磁转矩可表示为:
(2)
式中,ω为转子角速度;Te为电机电磁转矩。
BLDCM的运动方程为:
(3)
式中,J为电机转动惯量;TL为负载转矩;B为摩擦系数。
2 BLDCM换相转矩脉动分析
本文将以B相上桥臂VT3关断,C相上桥臂VT5开通为例,来对电机换相过程进行分析。
(1)换相开始前:
ib=-ia=I,ic=0
式中,I为换相相电流,并且假定其在换相过程中不改变。
(2)换相期间:
ea=-E,eb=ec=E,ua=ub=0,uc=Udc
式中,E为电机反电动势峰值电压,在换相过程中保持恒定。
即在换相开始前电机的电磁转矩可表示为:
(4)
在换相期间,式(1)可改写为:
(5)
(6)
(7)
由于定子绕组为星型连接:
ia+ib+ic=0
(8)
将上式与式(5)、式(6)、式(7)联立,求解得:
(9)
由于PWM开关频率很高,R带来的影响可以忽略,求解上述微分方程可得:
(10)
(11)
(12)
将式(10)~式(12)代入式(2),可得出换相期间的转矩为:
(13)
由此可得换相期间的转矩脉动为:
(14)
B相相电流从I下降到0所需的时间为:
(15)
C相相电流从0上升到I所需的时间为:
(16)
由式(14)~式(16)可得出BLDCM在不同的电机反电势幅值大小区间内换相时的三相相电流,如图3所示,同时得出如下结论:
(1)若Udc<4E,则B相关断时间t1小于C相开通时间t2,非导通相续流,换相期间电磁转矩减小。
(2)若Udc=4E,则B相关断时间t1等于C相开通时间t2,非导通相不发生续流,换相期间电磁转矩不变。
(3)若Udc=4E,则B相关断时间t1大于C相开通时间t2,非导通相续流,换相期间电磁转矩增加。
由上图以及式(13)可得,电机运转的一个周期内的电磁转矩可以分为两部分:
(17)
综上所述,换相阶段非导通相相电流发生波动进而产生换相转矩脉动,换相转矩脉动的抑制取决于非换相相电流的处理。因此,可以通过在换相阶段调节非换相相电流来降低换相转矩脉动,也可以使开通相相电流上升速度与关断相相电流保持相等来抑制换相转矩脉动。
3 基于改进型模型预测的控制方案
模型预测控制是一种对系统未来状态的预测来决定输入序列的离散算法。该方案利用驱动系统的离散方程和离散模型的提取,在计算下一个采样值的基础上预测系统的未来行为,并通过优化代价函数来确定最佳开关状态,以确保换相阶段非换相相电流保持恒定,进而降低换相转矩脉动。BLDCM框图如图4所示。
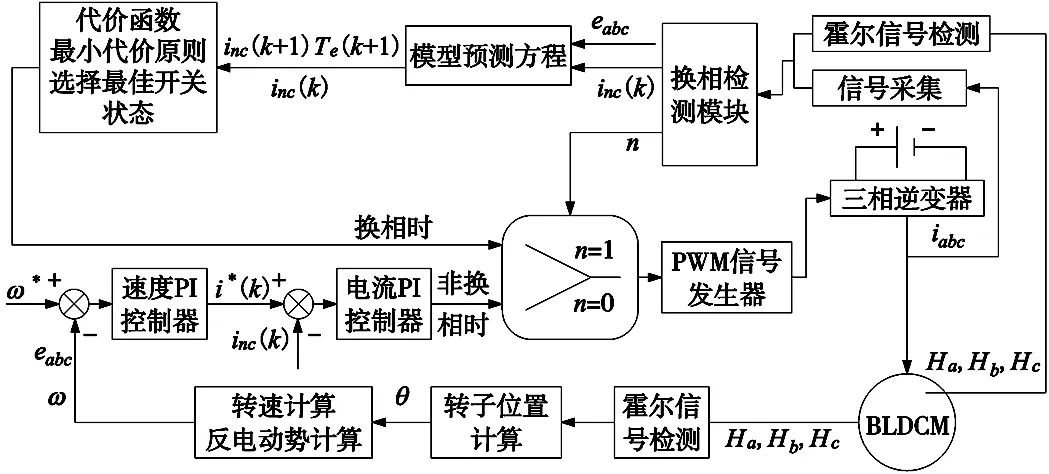
图4 基于改进型模型预测控制策略的BLDCM框图
仍以B相上桥臂VT3关断,C相上桥臂VT5开通为例,来对电机换相过程进行分析。非换相相电流被认为是最小化换相转矩脉动的关键参数。 基于式(1),推得非换相相电流预测模型如下:
(18)
(19)
将上述两式联立,得:
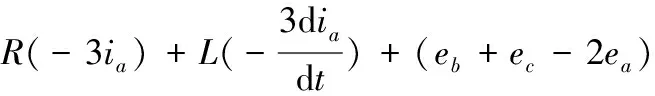
(20)
因此可得出非换相相电流的导数如下:
(21)
考虑到数据采样需要一定时间的采样周期,因此使用下式:
(22)
来离散化式(21),即可得到预测的ia如下:

(23)
式中,TS为采样周期;ia(k)为k时刻A相的相电流;ia(k+1)为(k+1)时刻A相的预测电流。
为了使转矩脉动得到更大程度的抑制,参考转矩可以被认为是:
(24)
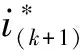
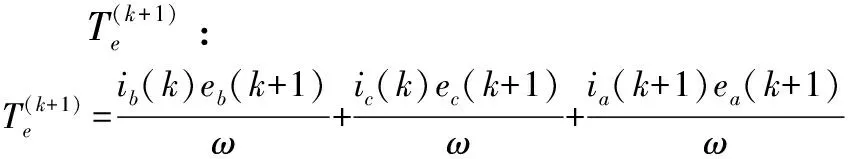
(25)
通过将预测转矩项添加到代价函数中,可以获得开关管的最佳切换状态以及更好的性能。由式(23)可知,在换相阶段,A相的相电流预测值主要受到三相相电压以及三相反电动势的影响。电机运行过程中,反电动势主要受转速影响,而相电压的大小取决于驱动板中逆变器开关管的导通状态。因此只要在k时刻选择最优的开关管导通状态,就能够得到(k+1)时刻最优的电流预测值,进而有效减小A相相电流的波动,达到抑制换相转矩脉动的目的。
综上所述,笔者所提出的新型基于模型预测控制的方案在换相阶段的代价函数定义为:
(26)
此外,在一个运行周期内,换相时刻的检测以及其持续时间是降低BLDC换相转矩脉动的重要前提。如图2所示,基于霍尔信号的上升/下降沿检测,是可以用来确定换相的起始时刻。因此笔者提出一种基于霍尔信号和相电流分析的精确测量换相时刻的方法,对照表1各个参数的变化,利用dsp中断采样,来进行换相时刻的检测。

表1 换相阶段各个参数的变化
4 仿真与实验分析
4.1 仿真分析
为了验证本文所提出的转矩脉动抑制策略,在MATLAB/Simulink环境下搭建了由三相逆变电路、BLDCM和控制系统组成的BLDCM驱动系统的仿真模型。电机的各个参数如表2所示。
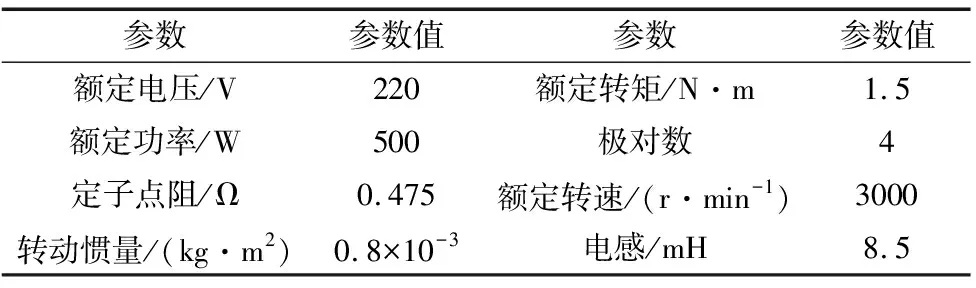
表2 无刷直流电机参数表
设定电机带负载恒定为1.5 N·m,以传统PI控制策略作为对照试验,分别在高速(3000 r/min)和低速(400 r/min)对电机相电流、转矩进行分析,以此来验证本文所提出的转矩脉动抑制策略的可行性与有效性。
转矩脉动率参照以下公式计算:
(27)
式中,Tmax、Tmin分别为瞬时转矩的最大值和最小值;Tavg为1.5 N·m;KT的值反映了转矩脉动的大小,KT越大,则转矩脉动较大,转矩脉动抑制效果越差;KT越小,则转矩脉动较小,抑制效果越好。
当电机转速为400 r/min负载为1.5 N·m,BLDCM稳定运行时,电流和转矩波形图,如图5所示。图5a为采用传统PI控制时(以B相电流为例),B相电流的波形图和转矩图;图5b为采用IMPC方法时,B相电流的波形图以及转矩图。使用PI方法控制时,在换相时刻,非换相相电流产生波动,转矩脉动率为36%。而使用IMPC方法控制时,在换相时刻,非换相相电流无明显波动,转矩脉动率为13%。
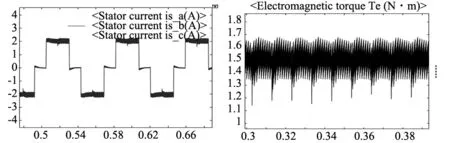
(a) 传统PI控制
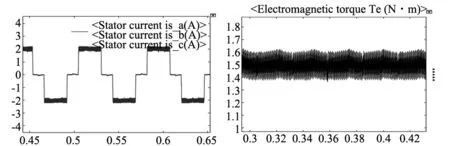
(b) IMPC控制
当电机转速为3000 r/min负载为1.5 N·m,BLDCM稳定运行时,电流的波形图以及转矩图如图6所示。图6a为采用传统PI控制时(以C相为例),C相电流的波形图和转矩图,转矩脉动率KT为53%;图6b为采用IMPC控制时,C相电流的波形图和转矩图,转矩脉动率KT为20%。

(a) 传统PI控制
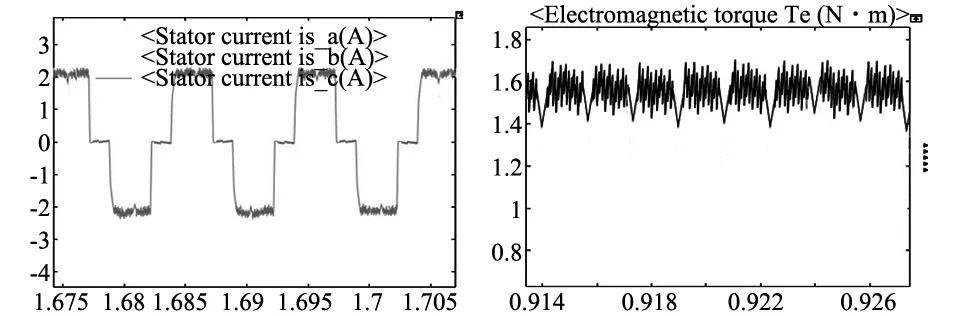
(b) IMPC控制
以上数据表明,电机在低速和高速运行时,采用传统PI方法进行控制,在换相阶段,非换相相电流发生明显波动,进而产生较大转矩脉动。采用IMPC策略进行控制,在换相阶段,非换相相电流无明显波动,转矩脉动率相较于传统PI方法分别降低23%和33%,转矩脉动抑制效果明显。
4.2 实验分析
以TI公司的DSP-TMS320F28335为控制芯片,一台功率为500 W的无刷直流电机为实验电机,搭建实验平台来验证本文所提出的控制策略的可行性。实验平台主要包括控制板、驱动板、开关电源、磁粉制动器、扭矩传感器、示波器等。实验平台实物图如图7所示。

图7 实验平台实物图
设定负载为1.5 N·m,电机处于低速阶段(300 r/min)稳定运行状态时,经过实验得到的两种控制策略下的系统转矩图如图8所示。根据式(26)可以计算出采用PI方法控制时,换相时刻电机的转矩脉动率约为38%,而采用IMPC方法控制时,换相时刻电机的转矩脉动率约为17%。转矩脉动率降低21%。

(a) 采用传统PI方案 (b) 采用IMPC方案
当电机速度升高到3000 r/min且处于稳定运行状态时,两种控制策略下的转矩图如图9所示。当控制系统采用PI方法进行控制时,换相时刻电机的转矩脉动率约为50%,采用IMPC方法进行控制时,电机处于换相时刻的转矩脉动率约为22%。转矩脉动率降低28%。
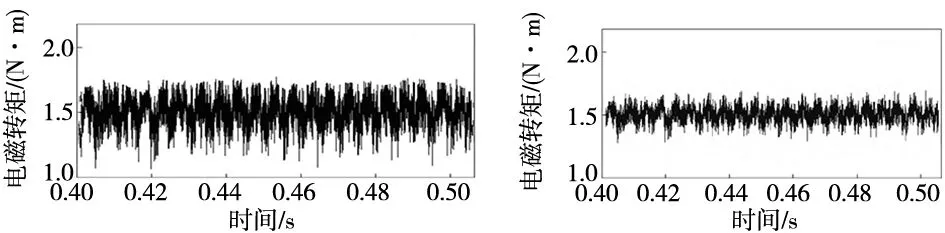
(a) 采用传统PI方案 (b) 采用IMPC方案
因此无论是在高速运行阶段还是低速运行阶段,采用传统PI控制策略的BLDCM,转矩脉动较大,而采用IMPC控制策略的BLDCM的转矩脉动相较于传统PI控制策略大大减小。
由于实验仪器本身的精度以及外部干扰的存在,使得实验波形与仿真波形存在一些偏差,但是实验结果与仿真结果定性的相对一致证明了基于改进型模型预测控制策略来降低无刷直流电机转矩脉动的可行性和有效性。
5 结论
本文提出一种基于改进型模型预测控制策略。通过分析换相转矩脉动的成因,建立该电机的预测模型,通过该模型的预测模型方程得到电流和转矩的预测值,并基于代价函数的最小代价原则得到开关管的最佳开关状态,以此来抑制换相阶段非导通相相电流波动,从而达到抑制无刷直流电机转矩脉动的目的。仿真和实验结果表明:所提出的控制策略使非换相相电流波动大幅减小、波形更加平滑,同时能够使转矩脉动控制在一个较小的波动范围内,极大的提高了无刷电机驱动系统的精度以及控制性能。

