多雨地区双块式无砟轨道湿态混凝土力学性能
杨荣山 ,李 莹 ,许钊荣 ,刘 佳
(1.西南交通大学高速铁路线路工程教育部重点实验室,四川 成都 610031;2.中国铁路设计集团有限公司,天津300308)
在潮湿多雨或排水不畅地区,水致病害是双块式无砟轨道服役期间的主要病害之一[1].由于轨道结构内部不均匀的湿度分布,使得混凝土的材料性能产生不同程度的变化,在高频列车荷载与水耦合作用下,轨道结构出现了道床板积水、轨枕松动和层间离缝冒浆等病害[2],给高速铁路的长期运营留下了隐患.因此,探明水环境中双块式无砟轨道湿度分布情况,开展该湿度条件下混凝土材料性能变化的研究,可为后续分析无砟轨道水致病害的形成机制及演变规律提供理论基础.
针对混凝土浸水软化的问题,Parrott[3]通过试验分析了混凝土结构表层与里层的干湿差异;王海龙等[4-6]利用细观断裂力学研究湿态混凝土的抗压强度,并开展了饱和与干燥混凝土力学性能变化试验研究;Li[7]通过实验分析了不同含水量下湿态混凝土强度变化规律,结果表明随含水量的增加,湿态混凝土的拉、压强度均呈降低趋势,水灰比越高的混凝土,其强度随湿度的变化越剧烈;侯东伟等[8]对干燥及湿态环境下的混凝土试件的弹性模量进行了测量,发现处于湿态环境中的混凝土弹性模量均比干燥环境中要高,增幅可达16.4%.
由此可见,当前研究多以宏观试验为主,虽能得到混凝土力学性能随含水量的大体变化趋势,但所得结果较为离散,不成体系,其技术无法脱离经验性的束缚.近年来,研究人员开始从不同尺度通过理论分析和数值模拟等手段对湿态混凝土力学性能进行预测.孙国文等[9]系统地介绍了混凝土从纳米尺度过渡到宏观尺度的建模过程;杜修力等[10]从细观层面提出了预测非饱和混凝土力学性质的两步均匀化方法;Bernard等[11]采用了多尺度的方法,从微观结构出发,向上一尺度输入参数,层层递进,预测了水泥基复合材料的弹性模量等.基于此,本文建立了水环境中路基段双块式无砟轨道湿度场有限元模型,分析了轨道结构湿度场分布特性.基于“等效均匀化”思想,开展混凝土基质多尺度计算,研究与轨道内部湿度场相对应的不同饱和度湿态混凝土的力学性能.
1 双块式无砟轨道湿度场计算
混凝土湿度场和温度场的控制方程、边界条件等均存在极高的相似度,不仅具有相同结构形式的表达式,其基本参量也一一对应.研究表明,基于这种相似性,将混凝土湿度场的基本变量及相关参数替换到温度场中即可将混凝土结构的湿度场问题转化为温度场问题进行处理[12-13].故本文利用ANSYS有限元软件的热分析模块对水环境中双块式无砟轨道的湿度分布情况进行了模拟分析.
1.1 湿度场计算模型
路基直线段双块式无砟轨道由支撑层、道床板及轨枕块等构成.假定所研究的双块式无砟轨道整体浸水程度相同,且在垂直方向上不受其他因素影响,即轨道各纵断面条件相同.在进行适当简化后,选取双块式无砟轨道横断面,采用PLANE55二维实体单元建立了二维湿度场有限元模型,如图1所示,模型所涉及各构件尺寸及材料参数如表1所示.
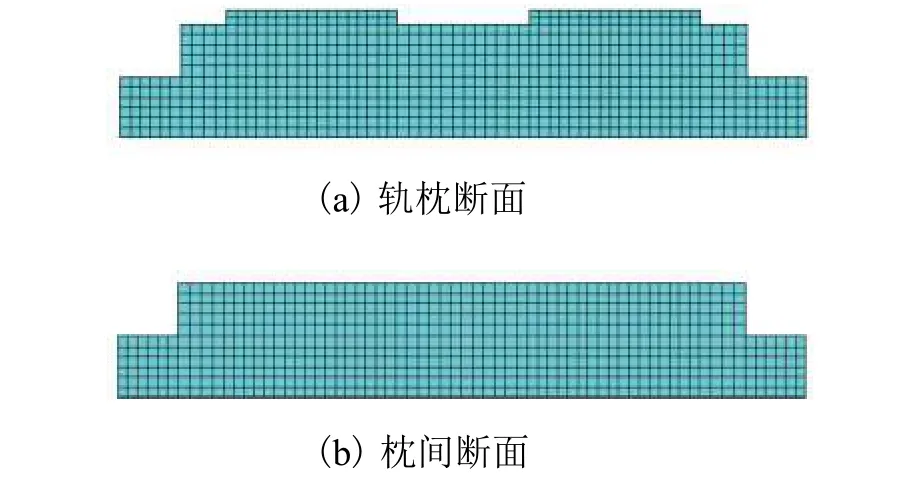
图1 双块式无砟轨道湿度场的二维有限元模型Fig.1 Two-dimensional finite element model of humidity field in double-block ballastless tracks
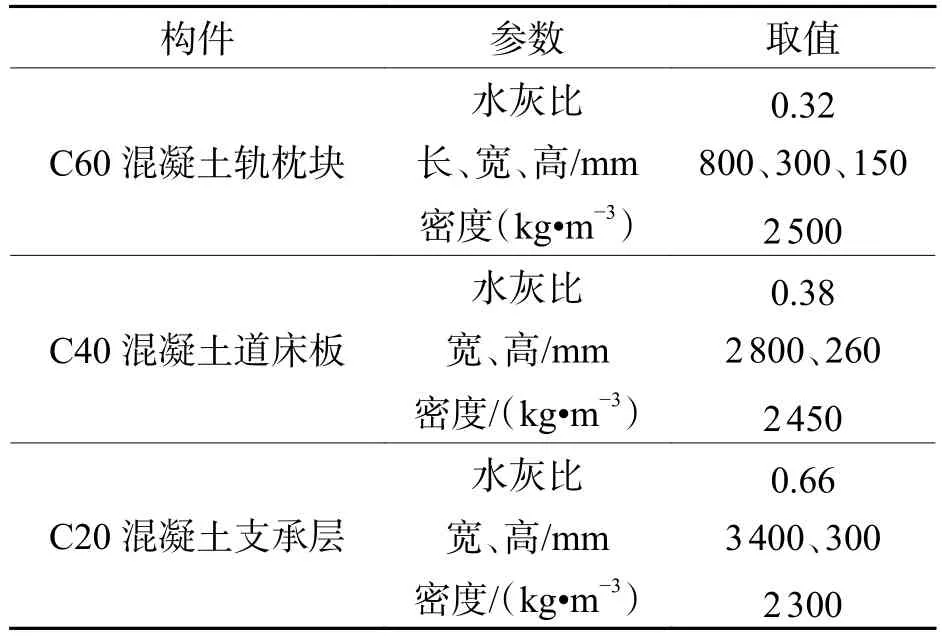
表1 双块式无砟轨道构件尺寸及材料参数Tab.1 Dimensions and material parameters of double-block ballastless track components
1.2 参数取值
1.2.1 湿度扩散系数
湿度扩散系数D是随自身周围湿度变化的函数,既有研究表明,周围湿度越大,扩散系数会迅速提高.当前计算湿度扩散系数的方法有:ANSYS优化法[14]、试算法[3,15]和 Bohzmann 变量法[16-17],但受测量精度和计算方法的影响,其取值不尽相同.本文选取通过ANSYS优化法得到的湿度扩散系数为
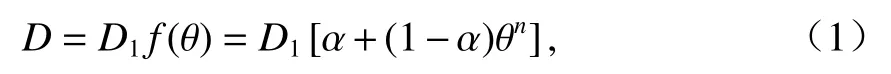
式中:θ为混凝土湿度;D1为θ= 100.00%时的最大湿度扩散系数,参考文献[17-19],D1= 1 × 10-5m2/h ;ƒ(θ)为湿度影响函数;α = D0/D1,D0为θ= 0 时的最小湿度扩散系数,α取值 0.05[18];n为曲线形状指数,一般取4 ~ 12,本文取8.
1.2.2 水分自耗率函数
自干燥效应会受混凝土水灰比、湿度、温度等多种因素的影响.混凝土自干燥过程中的水分自耗率函数[14,20-21]为

式中:kz为固定常数,取 0.426 37 d-1;nm为养护指数,受养护条件影响,一般取1.20,养护3 d取1.10,养护28 d 取 1.35;t为时间;h∞为常数,取值为0.00478×exp(kw/0.3068),kw为混凝土的水灰比.
1.3 边界条件及初始条件
满足混凝土湿度场控制方程的解并不唯一,为得到准确可靠的湿度场分布,必须确定其边界条件和初始条件.
在边界处混凝土结构与大气直接接触,存在混凝土表面湿度与其周围环境湿度的水分交换,计算如式(3)所示.

式中:θs为混凝土表面湿度;θe为周围环境湿度;β为表面湿度交换系数,单位为m/d或m/h,其取值与混凝土周围的温度、风速、表面粗糙程度及水灰比等因素相关[12],无风条件下,β= 5.28 ×10-3m/d.
路基地段双块式无砟轨道道床板混凝土在浇筑初期内部完全饱和,轨枕和支承层在浇筑道床板前均需进行喷水润湿处理.因此,本文将轨道结构的初始湿度设为100.00%,未覆水部位暴露于湿度为65.00%的外界大气环境中,底部基础湿度环境良好,支承层底面湿度设为70.00%.
1.4 湿度场分布
轨道浇筑完成后养护28 d,养护结束后继续放置60 d,混凝土自干燥作用基本完成.本文选取此时作为浸水的起始时间,即轨道结构于第89天开始浸水.考虑在极端降水情况下,轨枕、道床板及支承层表面均被外界水所覆盖,将覆盖水膜厚度设为2 mm.我国南方多雨地区雨季长达3 ~ 4个月[22],本文按3个月进行研究,故设轨道结构总浸水时长为90 d.
计算得到了处于水环境中的双块式无砟轨道轨枕区域与枕间区域的湿度场分布,如图2所示.由图可知:轨道结构浸水后,软枕区域和枕间区域结构内部湿度差的最大分别为38.41%和34.20%.同时,其内部的湿度分布情况也较为复杂,轨枕、道床板及支承层上表面浸水后,各部件表层的湿度场出现了明显的梯级分化.而道床板和支承层的侧面未被外界水所覆盖,始终暴露于大气环境中,持续向外界蒸发结构内部的自由水,故该处湿度最低,仅为60.00%左右.由于混凝土材料湿度扩散系数较小,浸水90 d后轨道结构的中心区域基本不受外界水的影响,仍保持着初始80.00%左右的湿度.此外,双块式无砟轨道的轨枕区域与枕间区域的湿度分布情况也不尽相同.
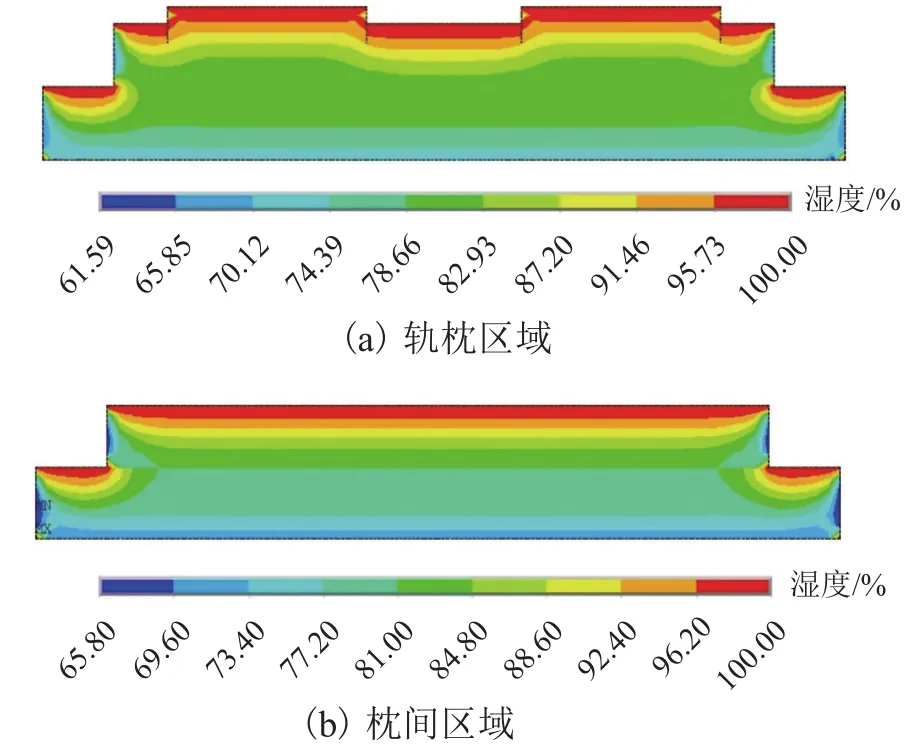
图2 水环境中湿度场分布Fig.2 Distribution of humidity field in sleeper area in water environment
可见,水环境中双块式无砟轨道结构内部的湿度分布存在非均匀性,且其内部的湿度差异较大.因此,在湿度影响下,双块式无砟轨道中各混凝土结构部件内部的力学性能将出现明显的不均一性.根据图2的计算结果,将水环境中双块式无砟轨道轨枕区域与枕间区域内部的湿度场划分为9个湿度区间,并取各区间的中间值作为代表值用于后续的计算分析,如表2所示.
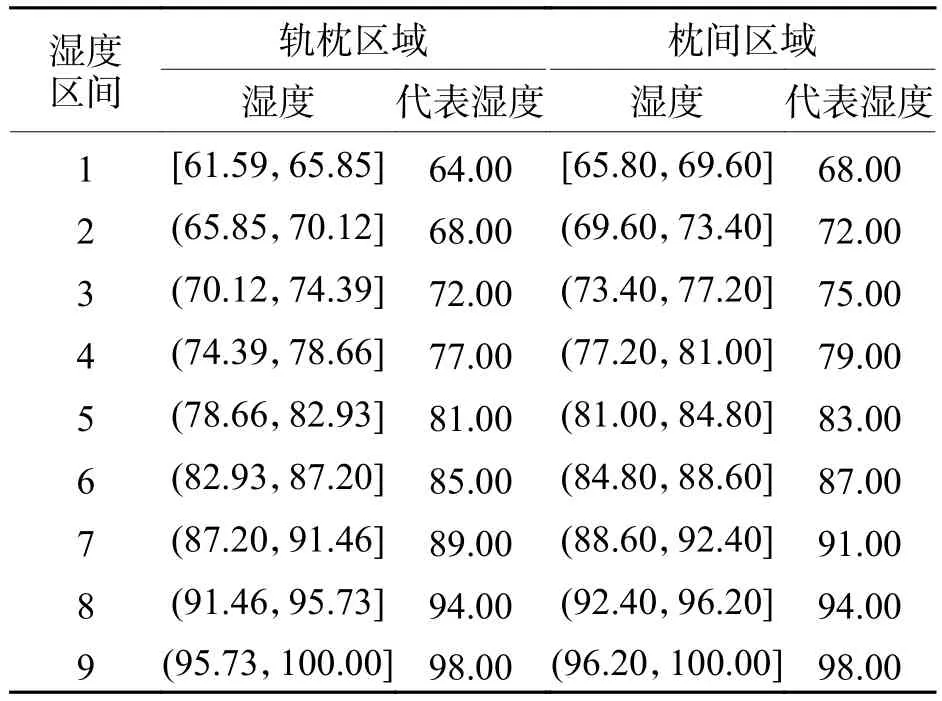
表2 水环境中双块式无砟轨道湿度区间及其代表值Tab.2 Humidity interval and representative values of double-block ballastless tracks in water environment %
2 湿态混凝土力学参数预测
非饱和湿态混凝土可以等效为由混凝土基质、饱和孔隙(饱和的毛细孔及气孔)及非饱和孔隙(部分饱和与干燥的毛细孔及气孔)组成的复合材料.基于文献[10],从纳观尺度出发,建立了混凝土基质的多尺度模型,在通过分子动力学模拟得到混凝土基质纳观组分(C-S-H胶束)的力学参数后,以此为基础展开混凝土基质的多尺度计算,最后通过两级均匀化法实现了对双块式无砟轨道混凝土部件内不同湿度状态混凝土有效力学性能的预测.
2.1 混凝土基质多尺度模型
混凝土是一种多孔、多尺度、多元多相的水泥基复合材料,应用不同尺度可以观察到不同的物质形态.参照前人的工作[23-26]构建了一个混凝土基质的多尺度模型,模型中不包含毛细孔、气孔和水,如图3所示.图中:HD为高密度材料;LD为低密度材料;CH为氢氧化钙.该模型涵盖了纳观、微观、细观及宏观4个层级,计算时以低层级模拟得到的参数作为输入展开对上一级层面的模拟,各层级的主要研究对象分别为混凝土基质、水泥砂浆骨架、硬化水泥浆体骨架以及纳米尺度下的水化硅酸钙凝胶体(CS-H凝胶).
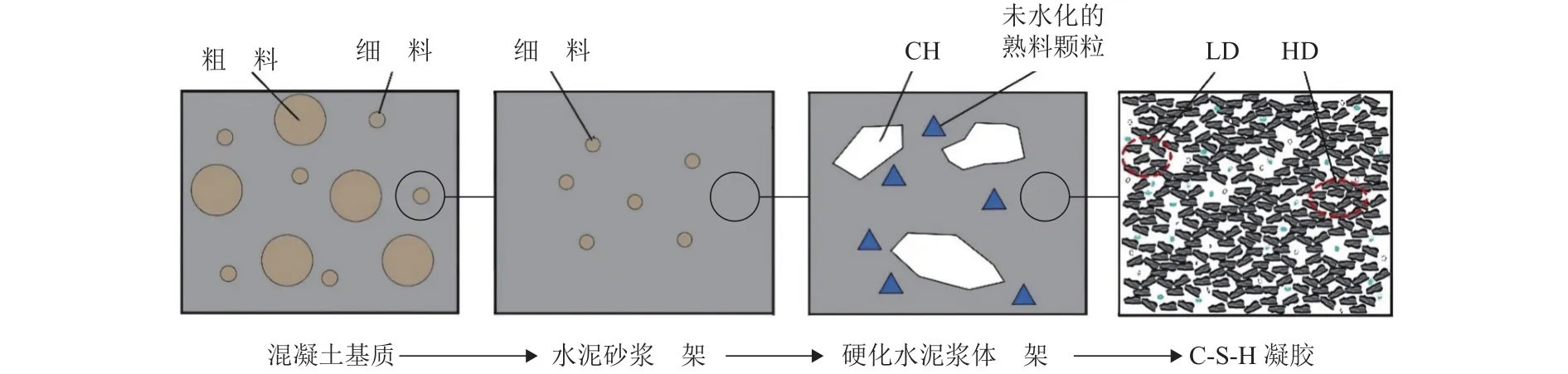
图3 混凝土基质的多尺度模型Fig.3 Multi-scale model of concrete matrix
模型中4个尺度下的主要研究对象均属于多相夹杂复合材料,可将各尺度下的研究对象逐级简化为含球形夹杂的各向同性线弹性两相复合材料,其具体组分如表3所示.
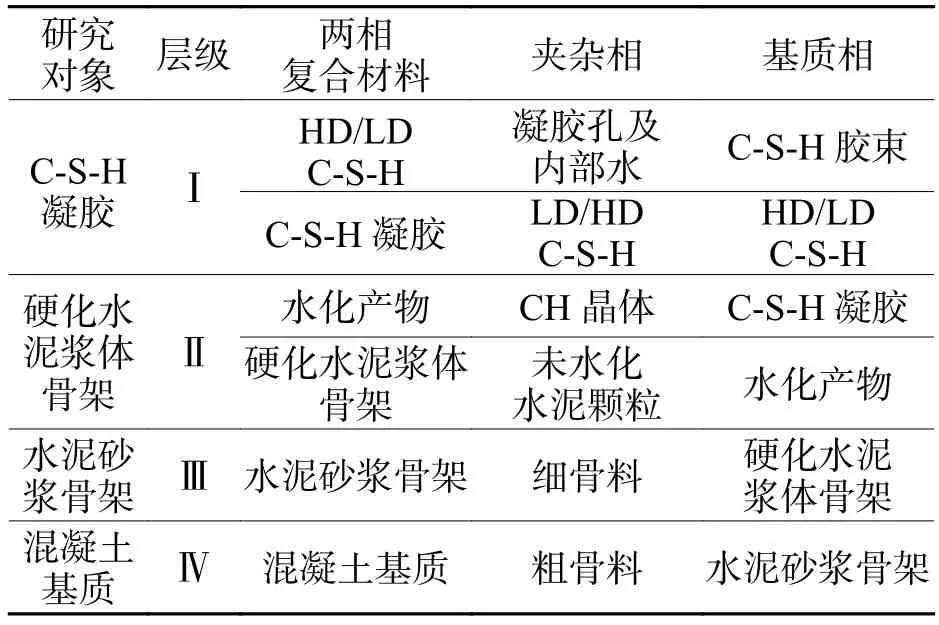
表3 各层级两相复合材料的具体组分Tab.3 Specific components of two-phase composite at each level
各层级夹杂相的力学参数如表4所示.基于纳观组分(最小基本单元)的力学参数和各层级的微结构信息后,利用Eshelby等效夹杂理论[27]与Mori-Tanaka方法[28]对各尺度研究对象进行逐级计算,最终得到混凝土基质的等效力学参数.其中,各尺度两相复合材料夹杂相的体积分数可根据混凝土材料的孔径分布、水灰比、水化程度及湿度状态等推算得到.
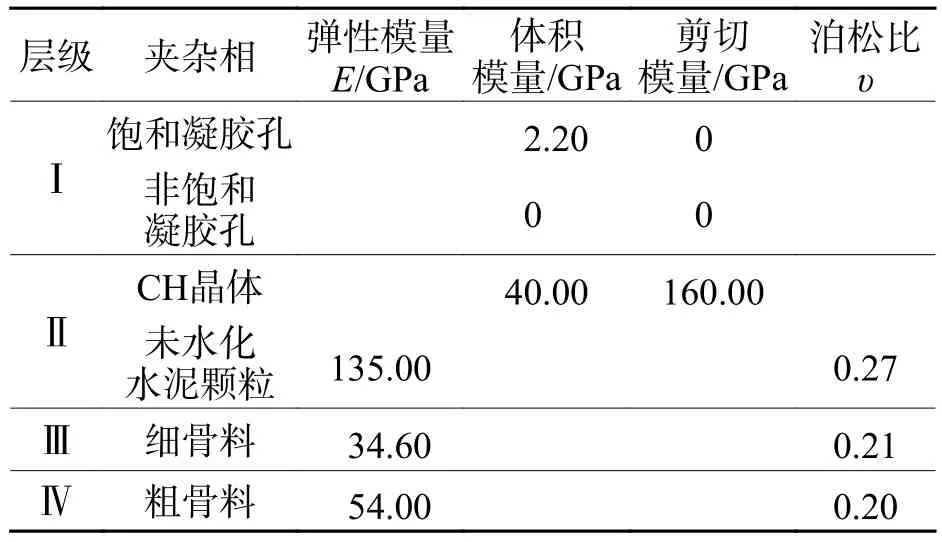
表4 各层级夹杂相的力学参数Tab.4 Mechanical parameters of inclusion at each level
2.2 水化硅酸钙的分子动力学模拟
作为混凝土纳观层面的主要组分, C-S-H不但具有十分复杂的内部结构和化学组成,其材料性能和物质组分还会随时间、空间以及所处环境条件等因素发生变化.为尽量获得真实客观的预测结果,本文利用Materials Studio软件建立了C-S-H分子模型,并对其进行相关的分子动力学模拟,在得到CS-H胶束的力学参数后,以此为基础展开对混凝土基质的多尺度计算.
2.2.1 模型创建
1) 初始模型的建立
① 建立硅酸盐骨架结构
通过Findit软件提取Hamid的Tobermorite 11 Å(Ca2.25[Si3O7.5(OH)1.5]·H2O)模型(钙硅比 C/S=1.0)的晶体参数[29],去除层间结构水(水分子和OH-基团),转为正交结构,并删除部分桥接 [SiO4]4-四面体以提高钙硅比.通过以上步骤得到的缺陷构型即为干燥状态下的硅酸盐骨架结构,三维模型如图4所示.图中:绿色球体代表Ca原子,黄色球体代表Si原子,红色及白色球体分别对应O原子和H原子.
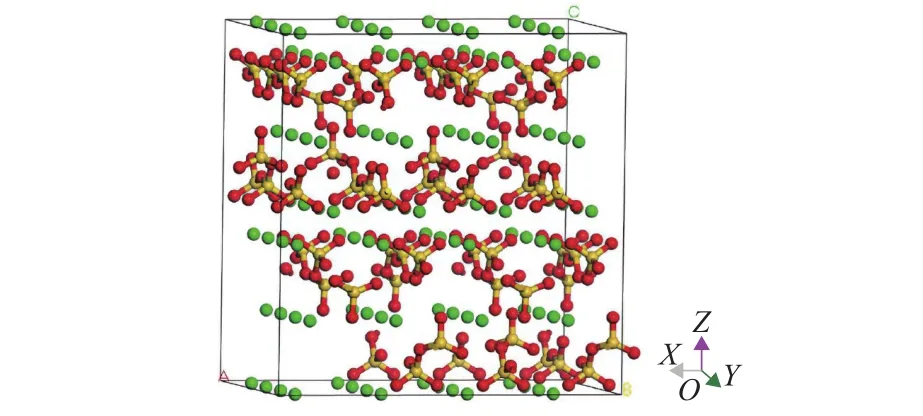
图4 干燥状态下的硅酸盐骨架结构Fig.4 Silicate skeleton structure in dry state
② 硅酸盐骨架结构的优化
使用Forcite模块对硅酸盐骨架结构进行优化,选择ClayFF力场[30],优化过程中选取Smart算法并采用周期性边界条件,在达到最低能量和收敛标准后优化结束.
③ 巨正则蒙特卡洛(GCMC)法吸水模拟
优化结束后,采用GCMC法引入水分子,执行Sorption模块中的Fixed Pressure任务,温度设置为293 K.任务结束后,硅酸盐骨架共吸附了89个水分子,模型密度达到2.31 g/cm3,由此得到了C-S-H分子模型的初始构型.
2) 初始结构动力学弛豫
弛豫过程选用GULP 模块,Task选择Dynamics.在等温等压系综(NPT)中温度设为293 K,压强设为3.567 kPa(水的饱和蒸汽压),经弛豫后的CS-H分子模型如图5所示,其化学组分式为(CaO)1.66(SiO2)(H2O)1.69,与实验测得的数据[31]相近.
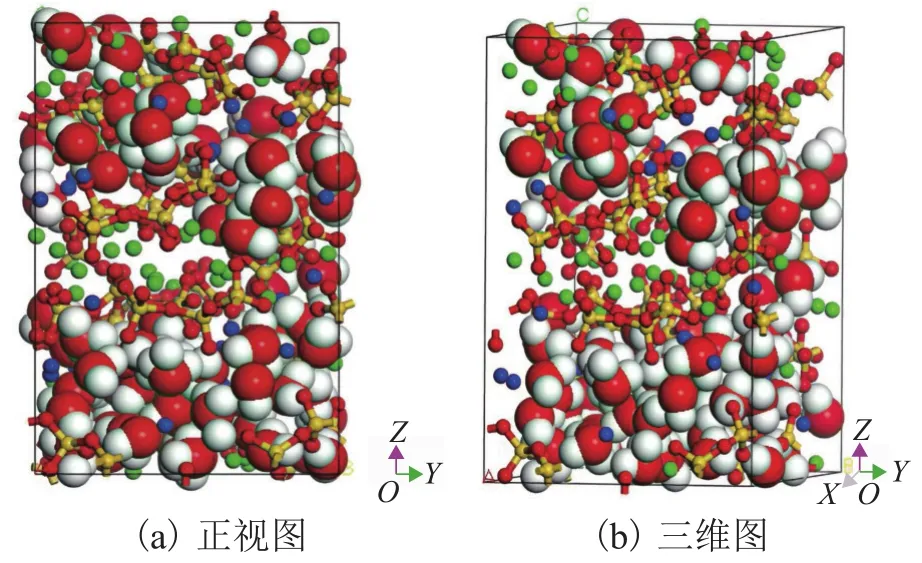
图5 弛豫后的C-S-H分子模型Fig.5 C-S-H molecular model after relaxation
2.2.2 力学性能的计算分析及验证
对弛豫后的C-S-H分子模型执行Forcite模块中的Mechanical Properties任务,在得到C-S-H单晶的弹性常数矩阵后利用VRH (Voigt-Reuss-Hill)近似方法计算获得C-S-H胶束的力学参数,如表5所示,可以看出,模拟结果处于合理的范围之内.

表5 C-S-H胶束力学性能参数Tab.5 Mechanical properties of C-S-H micelles
2.3 混凝土基质的多尺度计算
在获得C-S-H胶束的力学参数后,以此为基础沿着“C-S-H凝胶→硬化水泥浆体骨架→水泥砂浆骨架→混凝土基质”的路线逐级进行等效均匀化分析,从而得到水环境中双块式无砟轨道不同湿度状态下C20、C40及C60混凝土基质的等效力学参数,如表6所示.
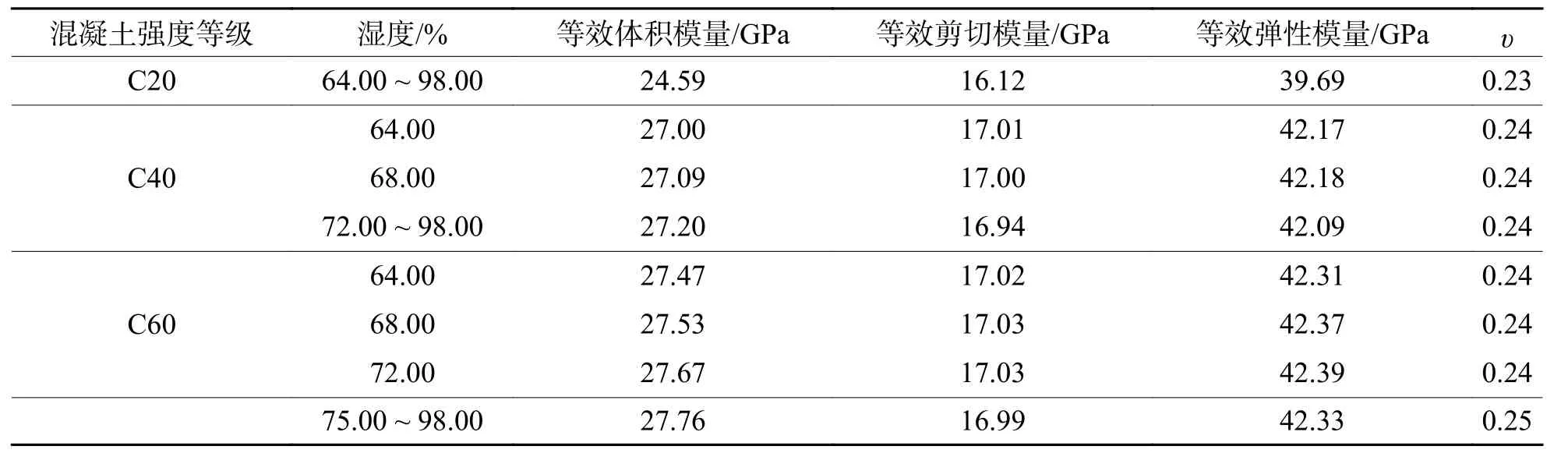
表6 混凝土基质等效力学参数计算结果Tab.6 Calculation results of equivalent mechanical parameters for concrete matrix
2.4 不同饱和度混凝土的两级均匀化计算
在得到混凝土基质的等效力学参数后,基于文献[9],将结构中非饱和的毛细孔及气孔均视为干燥孔,并将凝胶孔及其内部水分考虑为混凝土基质的组成部分,利用两级均匀化法实现了对不同湿度状态(饱和度)混凝土宏观力学性能的准确预测.
2.4.1 第一级均匀化
第一级等效体由混凝土基质与非饱和孔隙构成.在进行均匀化分析时,将非饱和孔隙视作夹杂随机分布在混凝土基质中.
2.4.2 第二级均匀化
在第二级均匀化过程中,将第一级等效体视为基质相,饱水孔隙视为夹杂相.对该两相复合材料进行均匀化分析,所得结果即为非饱和湿态混凝土的有效力学性能.
根据前述混凝土基质的等效力学参数,经计算[34]得到水环境中双块式无砟轨道轨枕区域与枕间区域各湿度区间混凝土的有效饱和度S、E和υ,分别列于表7与表8中.由表7、8可知:随着饱和度的增加,混凝土的弹性模量及泊松比均随之增大,但混凝土的强度等级越高,浸水后其弹性模量及泊松比的变化幅值越小.这是由于水的存在限制了孔周围混凝土基质向孔内挤压变形,而高强度等级混凝土的孔隙率较低,持水量较少,故其力学性能受湿度影响较小.当混凝土的有效饱和度由0变为100.00%时,支撑层、道床板及轨枕混凝土弹性模量的增幅分别可达到35.0%、19.5%、16.2%.
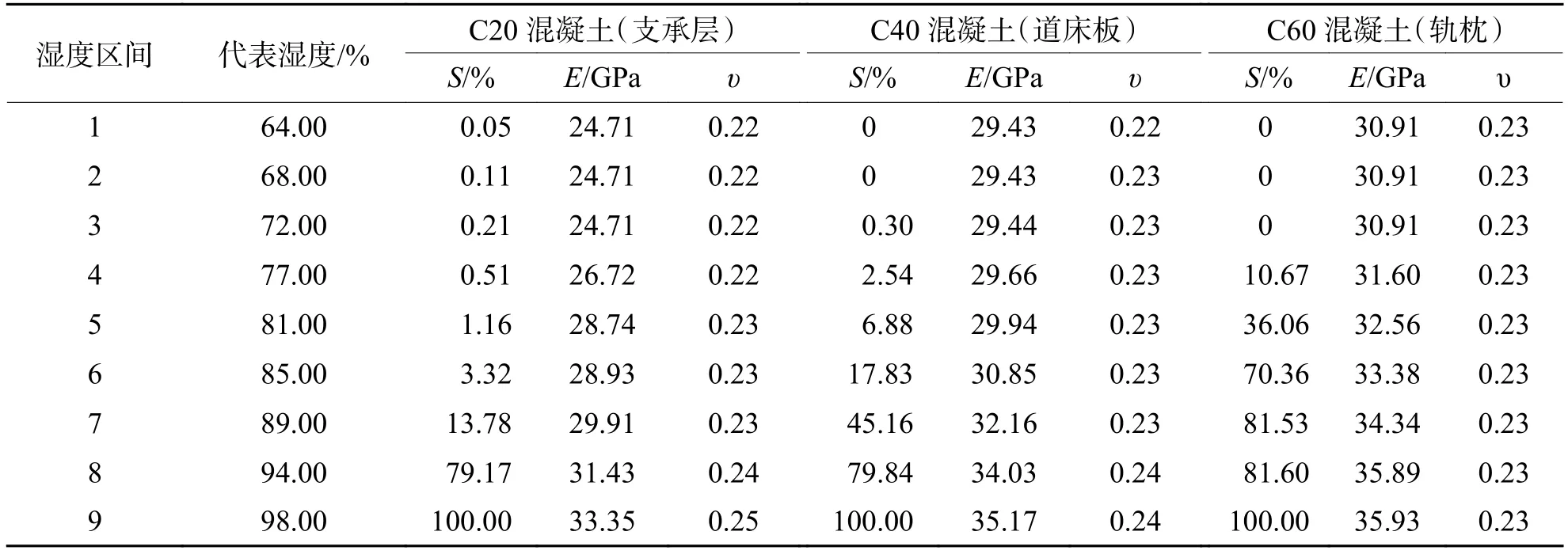
表7 轨枕区域不同湿度状态混凝土的有效力学参数Tab.7 Effective mechanical parameters of concrete in different humidity states in track-sleeper areas
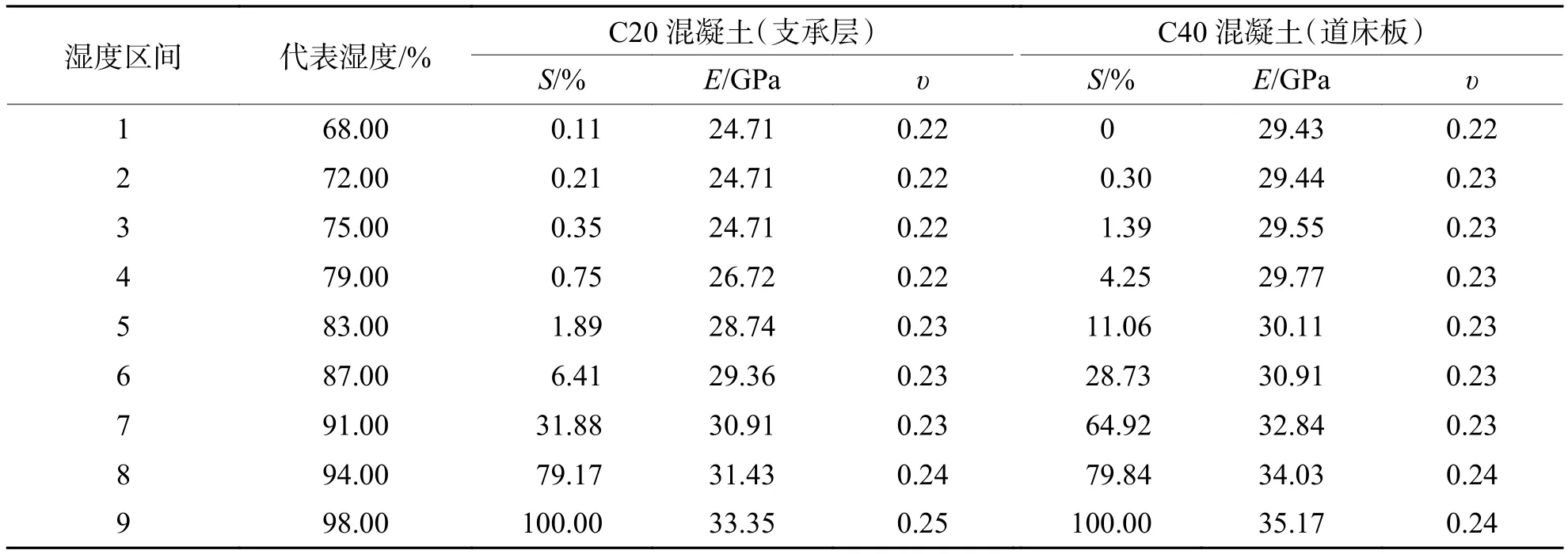
表8 枕间区域不同湿度状态混凝土的有效力学参数Tab.8 Effective mechanical parameters of concrete in different humidity states in areas between sleepers
3 结 论
1) 双块式无砟轨道的湿度场在纵、横及垂向上均存在不均匀性,且主要集中在结构表层.浸水后,结构表层湿度的梯级分化更为明显,轨道内部的湿度差异也明显增大,最大湿度差可达38.41%.
2) 对于水环境中的双块式无砟轨道,在不考虑其他复杂的环境条件及荷载作用下,混凝土弹性模量的最大增幅可达35.0%,但由于其内部不均匀的湿度分布,混凝土力学性能的变化幅度有所不同,导致轨道内部出现材料性能差异,这种差异将对轨道局部的力学行为产生一定影响.

