交直流双制式牵引供电系统钢轨电位特性分析

陈民武 ，付浩纯 ，谢崇豪 ，刘卫东 ，胥 伟

（1.西南交通大学电气工程学院，四川 成都 611756；2.中国中铁二院工程集团有限责任公司，四川 成都 610031）

交直流双制式牵引供电模式代表了城市轨道交通系统和市域铁路之间互联互通的发展方向，应用前景非常广阔，但目前在国内尚处于空白.交直流双制式牵引供电系统存在交直流过渡环节，在“车-轨”之间具有复杂和特殊的电气耦合与匹配特性.因此，研究交直流双制式牵引供电系统牵引回流特性、分析钢轨电位的变化规律具有重要意义.

国外交直流双制式牵引供电制式已有商业运营.在欧洲，德法边境的萨尔布吕肯市中心到勒巴赫采用直流牵引供电制式的轻轨线路与德国铁路有限公司采用交流供电制式的城际铁路在勒巴赫至埃岑霍芬的区段实施了共线运营[1]，但国内交直流双制式牵引供电系统的研究尚不多见.文献[2]分析了交直流双制式车辆受电方式的特点和转换方式.文献[3]建立了含有钢轨、埋地金属和大地的三级结构分布参数模型，实现了对杂散电流的预测.文献[4-6]研究了直流供电系统牵引回流和钢轨电位的分布特点及变化规律，以及钢轨电位限制方案.文献[7]基于CDEGS软件模型研究了铁路大型站场牵引回流系统回流特性.文献[8-9]建立了交流电气化铁路牵引回流系统模型，分析了钢轨电位的形成机制、分布特性及其影响因素.前期研究仅对交流供电制式或直流供电制式的牵引回流特性和钢轨电位分布单独分析，尚未研究交直流双制式供电制式下牵引回流的互扰对钢轨电位影响.

本文基于CDEGS构建了交直流双制式牵引供电系统牵引回流仿真模型，通过对钢轨复合电位交流分量和直流分量的共同约束，提出了适用于交直流双制式牵引供电系统钢轨复合电位限值.研究了无电区长度、过渡电阻和土壤电阻率等对钢轨复合电位的影响特性，分析了无电区段是否设置钢轨绝缘节时钢轨复合电位的分布特性.

1 交直流双制式牵引供电系统模型

1.1 计算模型

目前新建的跳磴至江津线为国内首条双制式线路，其中交流牵引供电区段采用单相工频25 kV交流制、带回流线直接供电方式，直流牵引供电区段采用DC 1 500 V架空接触网供电、走行轨回流的方式，供电示意如图1所示.采用CDEGS软件建立了交直流双制式牵引供电系统牵引回流仿真模型如图2所示，模型中各导线电气参数见表1.

表1 牵引供电系统导线电气参数Tab.1 Electrical parameters of wire of traction power supply system

图1 交直流双制式牵引供电系统示意Fig.1 Diagram of AC/DC dual-system traction power supply system

图2 交直流双制式牵引供电系统牵引回流仿真模型Fig.2 Simulation model of traction return current for AC/DC dual-system traction power supply system

交直流双制式系统中，交流区段和直流区段钢轨体现的电阻是不同的.由文献[10]可知，直流区段的钢轨纵向单位电阻为40.0 mΩ/km；由文献[11]可知，钢轨是铁磁材料，磁导率和钢轨电阻随通过电流发生变化，根据公式可得交流区段钢轨有效单位电阻为135.0 mΩ/km，单位内电感为0.44 mH/km.

1.2 直流区段牵引回流校验

基于交直流双制式牵引供电系统直流区段牵引供电设计参数，构建直流区段的“轨-排-地”结构电阻网络模型如图3所示，图中：ig为钢轨电流；uh为排流网对地电位；rog为钢轨对地过渡电阻；roh为排流网对地过渡电阻；Rg为钢轨纵向单位电阻；Rh为排流网纵向单位电阻；I为机车取流；l为机车至牵引变电所的距离.由文献[12]可得钢轨电位ug和排流网电流ih表达式为

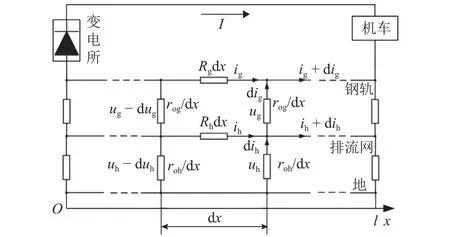
图3 轨-排-地电阻网络结构模型Fig.3 Resistance network structure model of rail-drainage net-ground

式中：λ1、λ2、k1、k2、C1～C4为边界条件确定的常数.

交直流双制式系统直流区段中，取I= 2 000 A，Rg=40.0 mΩ/km，Rh= 87.5 mΩ/km，rog= 15 Ω·km，roh=15 Ω·km，l= 2 000 m，混凝土层电阻率为1 000 Ω·m[13-14]，土壤电阻率为100 Ω·m，混凝土层厚度为0.6 m.钢轨下放置8根纵向钢筋，钢筋每隔50 m联结一次，来模拟实际的排流网结构，排流网不与变电所负极柜相连接.结构钢筋设置电阻率为1.1 × 10-7Ω·m，直径为0.016 m，计算结果与仿真结果如图4所示.

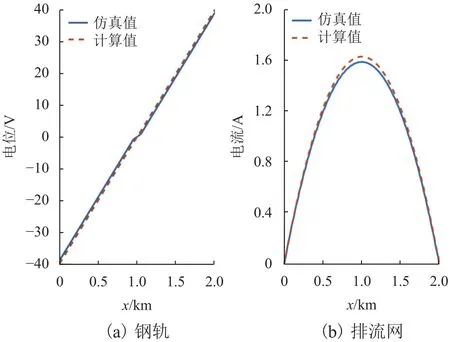
图4 解析计算与CDEGS仿真结果Fig.4 Analytical calculation and CDEGS simulation results

可见，双制式牵引供电系统中直流区段钢轨电位计算结果与仿真结果基本一致，最大误差为0.33 V，误差百分比为0.827%.排流网电流最大误差为42 mA，误差百分比为2.55%.

1.3 交流区段钢轨电位校验

交直流双制式牵引供电系统中牵引回流经钢轨返回变电所途中，由于钢轨与大地之间无法完全绝缘，流经钢轨的牵引回流会部分泄漏入大地，会引起铁路钢轨电位的变化.构造如图5所示单线牵引网等效电路，对钢轨电流和钢轨电位进行了理论分析.图中：z1和z2分别为接触网-地回路的单位阻抗和钢轨-地回路的单位阻抗，Ω/km；z12为接触网-地回路与钢轨-地回路间的单位互阻抗，Ω/km；y为钢轨对地单位导纳，S/km；ZE为变电所接地电阻，Ω；Z0为钢轨的特性阻抗，Ω.

图5 牵引网等效电路示意Fig.5 Diagram of equivalent circuit of traction network

由文献[15]可得

式 中 ：I˙T(x) 和U˙T(x) 分别 为 钢 轨 电流 和 钢轨 电 位 ；K为接触网对钢轨的耦合系数； γ 为钢轨与大地回路的传播常数，1/km.

交直流双制式牵引供电系统交流区段中，设置钢轨相对大地的过渡电阻为10 Ω·km、大地电阻率为100 Ω·m，线路全长15 km，变电所和机车分别设置在0和15 km处，假设机车取流为340 A.当不考虑变电所接地装置时，钢轨电位仿真与计算结果如图6所示.

图6 钢轨电位计算与CDEGS仿真结果Fig.6 Rail potential calculation and CDEGS simulation results

可见，交流区段钢轨电位的仿真结果与计算结果基本一致，最大误差不超过3.58%.因此，采用CDEGS软件建立的交直流双制式牵引供电系统仿真模型具有较高的计算精度，可以用于钢轨复合电位特性分析.

2 钢轨复合电位限值评估

交直流双制式牵引供电系统中，由于交流和直流牵引供电系统的交互作用，不能单纯通过交流或直流钢轨电位限制标准来评估钢轨电位，应进一步引入适用于交直流双制式牵引供电系统的钢轨复合电位限值.

IEC62128-3—2013[16]引入了接触复合电压的概念，当交流系统和直流系统存在交互作用时，为确保系统的正常运行以及保证电气安全，通过对接触复合电压交流分量和直流分量共同约束得到接触复合电压限值.当持续时间大于300 s时，交流供电制式和直流供电制式的交互作用区段内接触复合电压限值如图7所示.图中：阴影部分为接触复合电压允许范围；横坐标轴Udc为接触复合电压中的直流分量，V；纵坐标轴Uac为接触复合电压中的交流分量，V.

图7 长时工况下接触复合电压限值Fig.7 Combined touch voltage limit during long-term operation

依据上述接触复合电压的限值，本文通过对交直流系统中钢轨复合电位的交流分量和直流分量进行共同约束，得出适用于交直流双制式牵引供电系统的钢轨复合电位限值.

GB/T 28026.1—2018[17]给出了交流系统中长时工况下最大允许接触电压为60 V.根据德国铁路标准Gbr997.03，可接触电压与钢轨电位之比的推荐值为0.5.因此对于交直流双制式牵引供电系统，钢轨复合电位交流分量最大限值可取120 V.

《城市轨道交通技术规范》（GB 50490—2009）[18]中规定：正常运营条件下，正线回流轨和地间电压不应超过DC 90 V.因此，钢轨复合电位直流分量最大限值可取90 V.

结合接触复合电压的限值，可以得出交直流双制式牵引供电系统中长时间工况下钢轨复合电位限值，如图8所示.

图8 长时工况下钢轨复合电位限值Fig.8 Combined rail poteptial limit during long-term operation

目前，国内尚无交直流双制式牵引供电系统运营经验，对于无电区是否设置钢轨绝缘节暂无明确规定.下文对无电区是否设置钢轨绝缘节这两种工况进行量化分析，并依据钢轨复合电位限值进行评估.

3 无电区不设置钢轨绝缘节工况分析

本文仿真模型建立基于工程设计：交流牵引所1座，直流牵引所3座；交流区段长度为15 km、无电区长度为78 m、直流区段长度为4 km；混凝土层电阻率为 1 000 Ω·m、土壤层电阻率为 100 Ω·m；直流区段钢轨对地过渡电阻为15 Ω·km[19]、交流区段钢轨对地过渡电阻为10 Ω·km[20]；交流区段机车取流240 A，直流区段机车取流4 300 A；按照紧密运行组织排列，追踪间隔为3 min.

3.1 无电区长度影响分析

无电区长度对钢轨复合电位的影响尚不明确，江津—跳蹬（江跳线）考虑受电弓间距使得无电区不能短于78 m，同时由于机车惰行的安全使得无电区不能设计过长.因此，选取无电区段长度为78、150 m时这2种工况，分别计算不同无电区长度时钢轨复合电位的分布，如图9所示.

由图9可见：无电区不设置钢轨绝缘节时，不同无电区段长度下钢轨复合电位直流分量峰值均超过限值90 V.

图9 无电区长度对钢轨复合电位的影响Fig.9 Influence of free zone length on combined rail potential

此外，无电区长度的增加使得交直流区段的牵引回流相互干扰降低，导致无电区钢轨复合电位降低，但敏感度较低.主要原因是无电区段长度相比于交、直流区段长度过短，对地回流分布影响较小.

3.2 土壤电阻率影响分析

本文仿真模型的大地是混凝土和土壤两层结构，保持上层混凝土电阻率不变，选取土壤电阻率为 100、200 Ω·m 和 400 Ω·m 这 3 种工况，计算不同土壤电阻率时钢轨复合电位的分布，如图10所示.

由图10可见：土壤电阻率增大，交流区段和直流区段牵引回流相互干扰程度增强，导致无电区段钢轨复合电位的增大.此外，随着土壤电阻率增大，交流区段钢轨复合电位增大.

图10 土壤电阻率对钢轨复合电位的影响Fig.10 Influence of soil resistivity on combined rail potential

3.3 过渡电阻影响分析

钢轨对地的过渡电阻是影响钢轨复合电位的主要因素之一.对于直流供电系统，新建线路钢轨对地过渡电阻不应小于15 Ω·km，运行线路的不应小于3 Ω·km[19].因此，选取直流区段钢轨对地过渡电阻为 3、15 Ω·km和 30 Ω·km这 3种工况，计算不同过渡电阻时钢轨复合电位分布，如图11所示.

由图11可见：直流区段钢轨复合电位随直流区段过渡电阻增大而增大，且存在钢轨复合电位超标现象.此外，随着直流区段过渡电阻增大，牵引回流直流分量对无电区段和交流区段干扰程度减少，导致区段内钢轨复合电位直流分量降低.

图11 过渡电阻对钢轨复合电位的影响Fig.11 Influence of transition resistance on combined rail potential

4 无电区设置钢轨绝缘节工况分析

由第3节可知，无电区不设置钢轨绝缘节时，钢轨复合电位存在超标现象.工程设计上采取无电区设置钢轨绝缘节来阻断交直流区段中牵引回流的直接流通.因此，选取无电区设置钢轨绝缘节和无电区不设置钢轨绝缘节这2种工况进行对比分析，仿真数据如图12所示.

由图12可见：无电区设置钢轨绝缘节时，由于系统回流结构和参考地电位的改变，交流区段和直流区段牵引回流相互干扰大幅降低，导致直流区段钢轨复合电位直流分量峰值从103.92 V下降至60.20 V，满足限值要求.因此，为保障交直流双制式牵引供电系统的人身安全，可以考虑在无电区段设置钢轨绝缘节.

图12 钢轨绝缘节对钢轨复合电位的影响Fig.12 Influence of rail insulation joints on combined rail potential

5 结 论

1） 建立了交直流双制式牵引供电系统牵引回流计算模型，并将理论计算值和仿真值进行比较，验证了模型的正确性和有效性.

2） 通过对钢轨复合电位交流分量和直流分量共同约束，提出了适用于交直流双制式牵引供电系统的钢轨复合电位限值.

3） 当无电区不设置钢轨绝缘节时，无电区段长度增大则交直流区段牵引回流的互扰降低，导致无电区钢轨复合电位减小；土壤电阻率增大则交直流区段牵引回流的互扰增强，导致无电区段钢轨复合电位增大；直流区段过渡电阻越大，则直流区段钢轨复合电位越高.

4） 以国内首条双制式线路为例，无电区设置绝缘节后可以使钢轨复合电位直流分量从103.92 V降至60.20 V，保障了人身和设备安全.

致谢：中国中铁二院工程集团有限责任公司科研项目（KYY2018022（18-20））.