基于行车安全场模型的交叉口车辆控制算法

金立生 ，郭柏苍 ,，谢宪毅 ，华 强 ，郑 义

（1.燕山大学车辆与能源学院，河北 秦皇岛 066000；2.吉林大学交通学院，吉林 长春 130022）

无信号交叉口随着车辆数目增多，容易出现严重拥堵、事故频发的现象，致使路网的通行效率显著降低.自动驾驶和车联网等先进技术的发展，促进了以车车/车路通信为基础的车路协同技术的发展[1-3].因此，提升网联自动驾驶车辆在无信号交叉口的协作效率，降低行车风险已成为研究热点之一.

国内外学者对交叉口内车辆协同控制开展了大量的研究.Dresner等[4]将预留思想融合到算法设计中，根据交叉口区域内车辆申请路权的优先顺序，按照先到先分配的原则分配时间和空间资源.Choudhury等[5]利用虚拟编队控制概念，确保车辆可以不停车而通过交叉口.Lee等[6-7]开发了一种车辆交叉口协同控制算法，通过最小化冲突车辆在交叉口的轨迹重叠长度，避免每对相互冲突的车辆同时在交叉口区域出现.Kamal等[8]借助模型预测控制框架，提出一种车辆交叉口协调方案（vehicle intersection coordination scheme ,VICS），阻止冲突车辆同时靠近碰撞点，最大限度减少车辆在交叉口区域碰撞的风险.

以上研究对于减少车辆冲突有一定效果，但没有充分考虑人车路闭环系统各要素间的综合作用，一旦车辆的行车环境发生变化，就容易导致车辆协同控制算法失效，算法对环境的适应性和鲁棒性表现不佳.因行车安全场理论[9]能动态反映人-车-路之间动态变化的特点，可以相对准确地评价车辆在复杂交通场景中的行车风险.因此，近年来越来越多学者借助于场论思想开展研究.Nakaoka等[10]基于风险预测模型提出了一种基于道路摩擦系数和驾驶员特征的前向碰撞预警算法.Matsumi等[11]借助人工势能场预测交叉口车辆潜在的行车风险，设计了一种自动驾驶车辆制动控制系统.Sattel等[12]利用势能场理论和弹性理论，提出了一种自动驾驶车辆路径规划方法，并实现了车辆紧急避撞和车道保持功能.吴剑[13]基于行车安全场理论设计了一种能够适用于多车场景的车辆碰撞预警算法.贺启才[14]以行车安全场模型为基础，设计了以主动避撞为创新点的车辆轨迹规划控制器.

行车安全场理论在车辆跟驰与路径规划有着重要的应用.在以往研究中所依据的行车风险分析评价方法对外界交通参与者可能引发的潜在风险要素考虑不全面，未充分考虑人-车-路中各个方面的特性和影响等问题，同时也难以描述人-车-路三者之间的耦合机制.目前，将行车安全场理论应用于交叉口内车辆协同控制的研究也较少.为此，本文针对网联自动驾驶环境，以行车安全场理论为基础，借助模型预测控制框架，提出一种基于模型预测行车风险场最小化算法（model predictive control-based driving risk minimization algorithm, MPC-DRMA）.

1 交叉口冲突特性分析

按车辆发生碰撞时冲突角度的差异，并根据冲突类型对通行效率的影响程度，冲突可划分为：交叉冲突、换道冲突、追尾冲突，如图1所示.

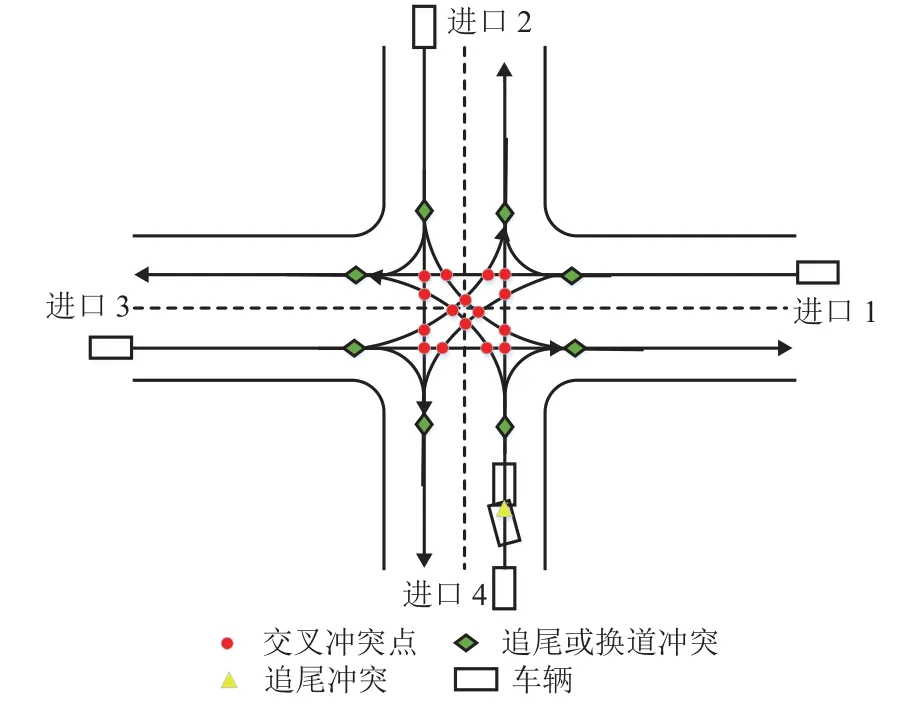
图1 交叉口冲突类别分布Fig.1 Distribution of intersection conflict categories

本文所提算法针对图2所示的交叉路口，每一进口道含有两条车道，分别为左转直行和右转直行.图中数字代表车道编号.

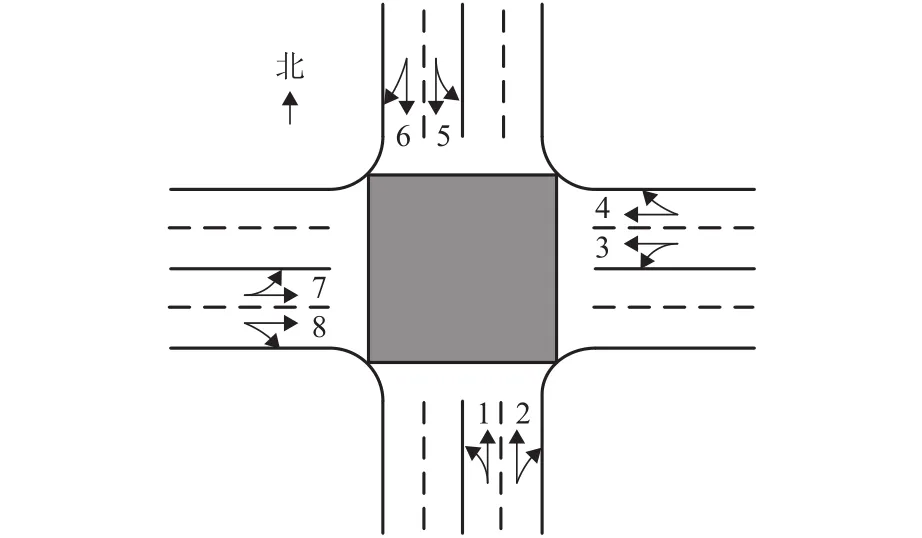
图2 无信号交叉口示意Fig.2 Schematic diagram of unsignalized intersection

根据车辆间的冲突情况，制定交叉口相位冲突表，如表1所示.表中：车道表示车辆在交叉口各车道之间的行驶意图，0表示车辆行驶相位之间不存在冲突关系，1表示车辆行驶相位之间存在冲突关系.以南向北入口为例，该路口存在以下的冲突类型：右转与左侧直行、右转与对向左转、直行与左侧直行、直行与右侧直行、直行与对向左转、直行与左侧左转、直行与右侧右转、直行与右侧左转、左转与左侧直行、左转与右侧左转、左转与左侧左转、左转与右侧直行、左转与对向右转.

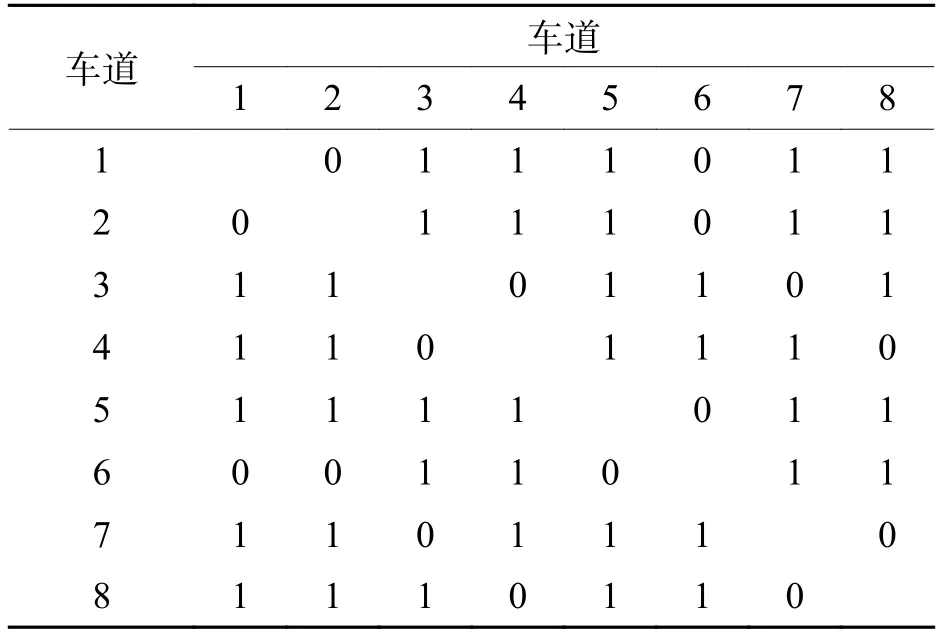
表1 交叉口相位冲突Tab.1 Phase conflict at intersection

2 基于行车安全场的控制算法模型

行车安全场由在道路上运动物体所产生的动能场、静止物体所产生的势能场和驾驶人相关元素确定的行为场共同组成[9].车辆行车安全场的通用模型表示为

式中：ES为行车安全场场强；ER为势能场场强；EV为动能场场强；ED为行为场场强.

2.1 势能场模型

静止物体分为能对行车造成实质性影响和不会与车辆发生碰撞只起约束作用的两类，本文仅考虑对行车造成实质性影响的第一类静止物体.通过对道路上的静止物体所产生的行车风险分析，第一类静止物体i在周围形成的势能场如式（2）所示.

式中：矢量ER_ij为处于点 (xi,yi) 处的第一类静止物体i形成的势能场在点 (xj,yj) 的场强矢量，场强越大，则施加的风险越大， (xi,yi) 为物体i的质心坐标，x轴沿车辆行驶方向，y轴垂直于车辆行驶方向；rij为点 (xi,yi) 和点 (xj,yj) 之间的矢量距离，场强方向与rij相同；k1和G为待定系数；Mi为物体i的等效质量；Zi为 (xi,yi) 处道路条件影响因子.

2.2 动能场模型

通过对道路上的运动物体所形成的行车风险具体分析，处于 (x,y) 处的运动物体i所产生的动能场在点 (xj,yj) 位置的场强矢量为

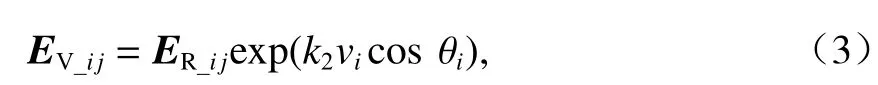
式中：k2为待定常数；vi为物体i的速度； θi为物体i速度方向与rij的夹角.

速度相同时， | θi| 越小， c osθi越大，EV_ij值越大，行车风险越高.当车辆沿运动物体方向靠近时，θi=0， c osθi=1 ，此刻行车风险最大，发生碰撞的概率最大.

2.3 行为场模型

一般来讲，假定外部条件相同，经验丰富的驾驶人相比于新手驾驶人所产生的行为场的场强更小，即驾驶行为更为合理.驾驶人对行车安全的影响通过车辆传递至外部的交通环境.由此，可以利用表征驾驶人特性的驾驶人风险因子和其驾驶的车辆产生的动能场场强的乘积表示行为场场强，如式（4）所示.

式中：ED_ij为车辆i形成的动能场在处的行为场场强；Dri为车辆i驾驶人的风险因子.

考虑到本文研究以网联自动驾驶车辆为环境背景，场景内车辆全部为网联自动驾驶车辆，没有驾驶人施加的影响，也就不存在行为场，因此，行为场场强ED为0，行车安全场只包括势能场和动能场.可将无信号交叉路口处车辆的协调控制问题转化为求解带有约束条件的非线性优化问题.由于模型预测控制易于求解带有约束的非线性优化问题，同时在车辆运动规划和运动控制领域中有着十分广泛的应用[15-16]，故本文利用模型预测控制理论设计车辆协同控制策略.

MPC-DRMA算法的目标函数为

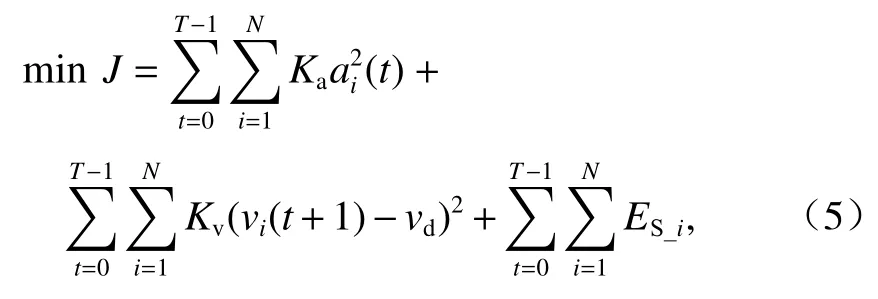
式中：J为行车风险；N为控制时域；T为预测范围的时间跨度；vd为期望车速；ai(t) 为车辆i在时刻t的加速度；Ka、Kv分别为加速度和速度的权重系数；ES_i为车辆i所受到的行车风险场场强的大小.

目标函数J包含3个成本项：第1项表示车辆加、减速度的变化程度；第2项表示实际车速与期望车速间的偏离幅度，最小化1、2项是从确保车辆行驶过程平顺性和舒适性的角度考虑；第3项表征的是车辆总的行车风险，包括势能场和动能场，表示车辆在驶过交叉路口过程中行车安全场的大小.车辆i受到的行车风险场场强为

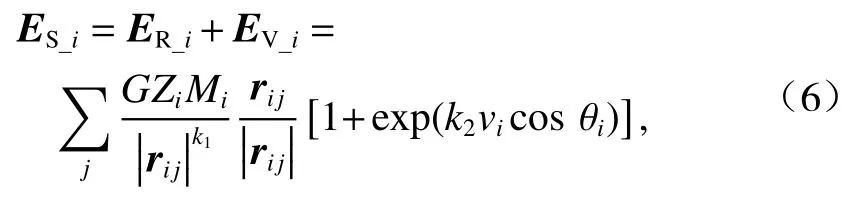
式中：ER_i、EV_i分别为车辆i所受到的势能场场强、动能场场强.

MPC-DRMA算法的约束条件包括行驶车速变化、车辆速度、安全车头时距、冲突相位间隔距离和转弯.

1） 行驶车速变化的约束

在行驶过程中频繁进行加速、减速会直接加剧行车的风险，因此，有必要对车辆的加速度ai(t)设定约束，具体表示为

式中：amax、amin分别为车辆加速度的最大值和最小值.

进一步，可将式（7）转化为

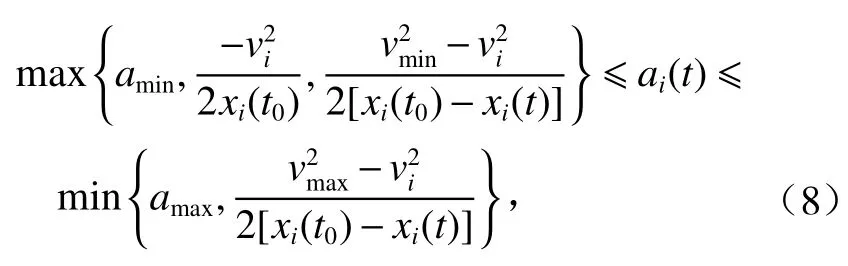
式中：t0为当前时刻；vmax、vmin分别为最高车速、最低车速.

2） 车辆速度约束

为保证路网通行效率和车辆实际情况，对车辆的行驶速度设置约束，包括最高车速、最低车速和转弯行驶车速，表示为

式中：vc为转弯行驶车速.

3） 安全车头时距约束

同一车道内前后车辆之间应保持一定的安全时距.为减少计算量，设定安全时距h=1s.时刻t0车辆i和车辆i+ 1轨迹安全时距应满足式（10）.其中，车辆i更接近交叉路口的停止线.

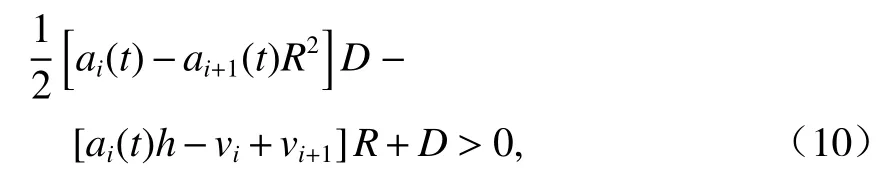
式中：D、R为计算的中间变量[17]，D=a(t)h2/2-vh-

4） 冲突相位最小间隔距离

为了避免处于不同道路相位上的车辆发生碰撞冲突，需要满足式（11），即能够在安全区域内计算得到最优解，以避免车辆在交叉路口发生碰撞.

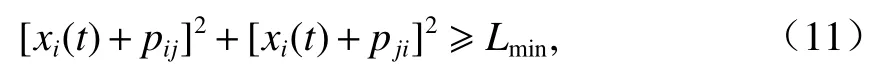
式中：Lmin为车辆中心点最小间隔距离；pij、pji为车辆i和j质心点到相应碰撞点的距离，如图3所示.

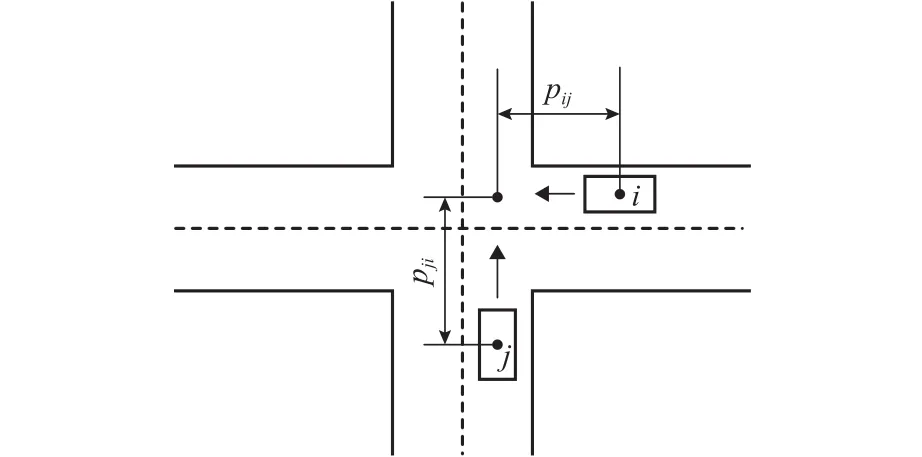
图3 无信号交叉口车辆冲突示意Fig.3 Vehicle conflict at unsignalized intersection

5） 转弯限制

车辆在交叉口转弯行驶时，需要考虑车辆本身的运动学条件，车辆转弯的横向加速度为

式中：Rc为车辆的最小转弯半径.

从通行角度来讲，如果车辆的转弯半径较大，则应以相对更高的速度转弯行驶，以减少对通行效率的影响，同时应满足车辆稳定性约束.故转弯约束为

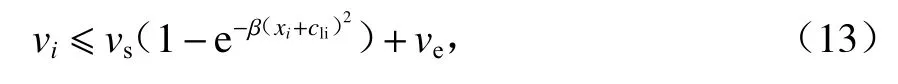
式中： β 为常数；cli为交叉口的起点和中心点之间的距离；vs、ve分别为车辆在交叉口起点和终点的速度.

赋予vs和ve较高的值，确保vs+ve＞vd.当|xi+cli|=0（在交点中心）时，vi≤vs；当 |xi+cli|＞0 （车辆距离交叉路口距离较远），此刻约束变为vi≤vs+ve.

3 仿真试验结果与分析

3.1 仿真试验设置

试验场景为孤立的双向四车道十字形交叉路口，以VISSIM与MATLAB为基础，搭建耦合仿真试验平台.利用Visual C ++实现VISSIM与MATLAB的耦合连接，包括建立VISSIM COM接口、加载交通路网、设置仿真参数、定义VISSIM元素（如网络对象、路端属性、车道数量、车辆数目、数据采集器、路径决策和检测器的评价、车辆参数等）以及基于行车安全场模型的模型算法.另一方面，在搭建仿真平台的过程中，由于VISSIM和MATLAB需要安装在 Windows平台，而 NS3则是安装在 Ubuntu平台，故可通过C ++ 使不同平台的Socket编程以及Socket的阻塞特性实现时间同步处理.VISSIM负责将路网及车辆信息给优化器，MATLAB负责对近似得到的非线性优化问题进行求解.

选取总的延误时间、行程时间和通行能力为机动性指标，选取冲突数目为安全性指标，依托于安全评估模型[18]对比分析算法的综合性能.

为了有效求解优化函数，结合内点法（interior point method，IPM）[19]和混合蛙跳算法（shuffled frog leaping algorithm，SFLA）[20]提升函数求解的计算速度，提高算法的实效性.

本文基于Synchro 7开发交通信号灯最优配时方案，用以获取路段最大服务交通量与基本通行能力之比 （volume to capacity ratio，VCR）.选取 40 个仿真场景并为场景设置不同的VCR，为消除随机性的影响，利用不同的随机种子对每一场景重复仿真40 次.最后，选取感应控制（actuated control，AC）作为对比试验进行评价分析.仿真参数如表2所示.

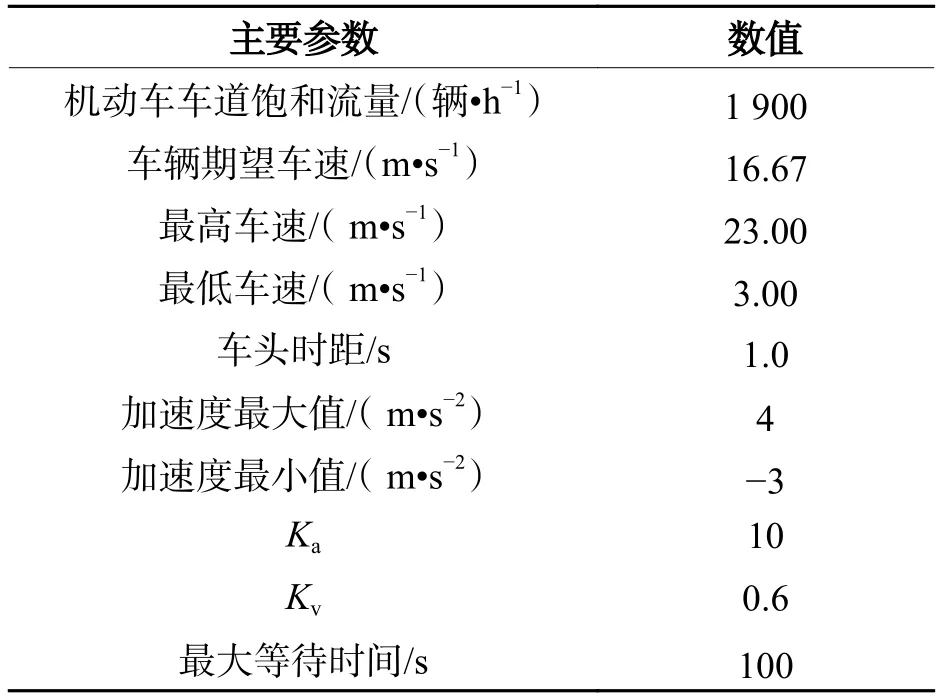
表2 仿真参数Tab.2 Simulation parameters

此外，与转弯速度有关的约束条件设置为vs=14m/s ， β =0.003 ，左转弯车辆ve=8m/s ，右转弯车辆ve=10m/s ，左转行驶时的最小转弯半径为40 m，右转行驶时的最小转弯半径为25 m.对于所有车辆，设置风险函数参数中碰撞风险的最大值为1 000，驾驶人风险感知水平数值为0.005.车辆长度、宽度分别设置为4.60 m和1.65 m.交叉口参数Lmin= 7 m，Rc= 10 m，离散时间步长为0.5 s，预测时间窗为7.0 s.

3.2 结果分析

3.2.1 车辆碰撞冲突分析

利用安全评估模型（surrogate safety assessment model，SSAM）对仿真试验中车辆的轨迹数据进行滤波处理，如图4所示，图中红色点为交叉冲突，绿色点为追尾冲突，蓝色点为换道冲突.由图可知：交叉路口内以交叉冲突形式为主，追尾冲突则分布于交叉路口驶入的路段，换道冲突则多发生于与交叉路口紧邻的路段.AC是目前主流的信号控制模式，因此，本文选择AC作为对比试验，利用 VISVAP[21]编写感应控制程序，实现对车辆运动的诱导控制.相比于AC算法，MPC-DRMA算法使交叉口冲突的数目大幅减少，在车辆驶过交叉路口的过程中，碰撞风险也显著降低.

图4 车辆冲突类别示意Fig.4 Schematic diagram of vehicle conflict categories

3.2.2 行车风险改善情况分析

车辆在通过交叉路口过程场强强弱的起伏分布状况如图5所示.假定网联自动驾驶环境足够理想，相比AC，MPC-DRMA算法的车辆行车风险强度、分布密度都有显著的降低，车辆风险场强的峰值有所减小，并且缩小了车辆行车风险的分布区域范围.这是因为MPC-DRMA算法引入了行车安全场的相关理论，并且充分考虑了车辆实际外形尺寸的影响.

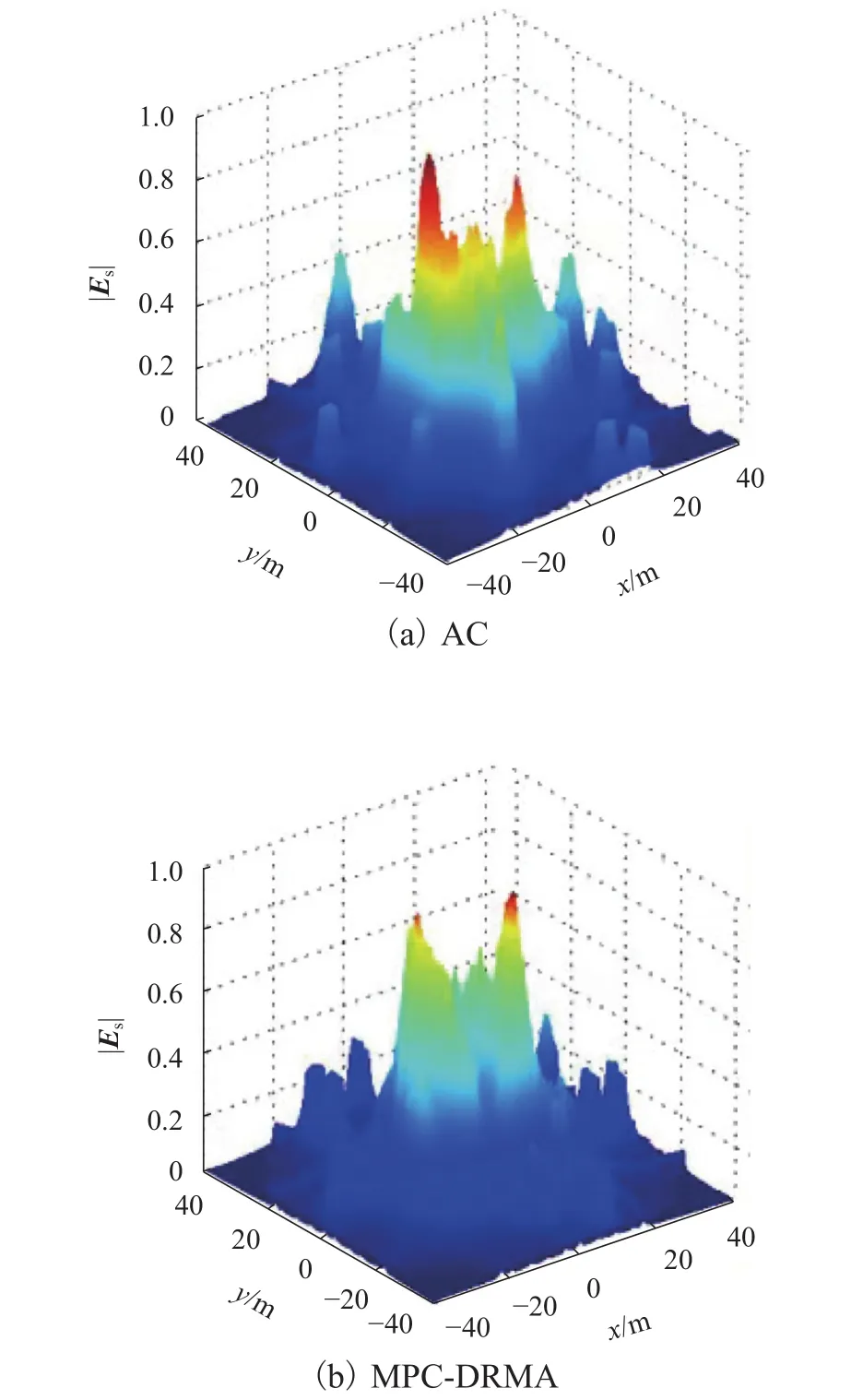
图5 车辆冲突场强分布三维图Fig.5 Three-dimensional diagram of field intensity distribution for vehicle conflict

以俯视角度观测到的车辆驶过交叉路口过程的场强分布如图6所示.本文所提算法不仅能够有效保障车辆在交叉口内的行车安全，特别是对于接近交叉路口时形成的行车风险也有不同程度的改善.值得注意的是，一方面，所预测的车辆行驶轨迹具有一定的不确定性，未能彻底消除碰撞冲突；另一方面，无法保证寻优算法始终存在最优解.

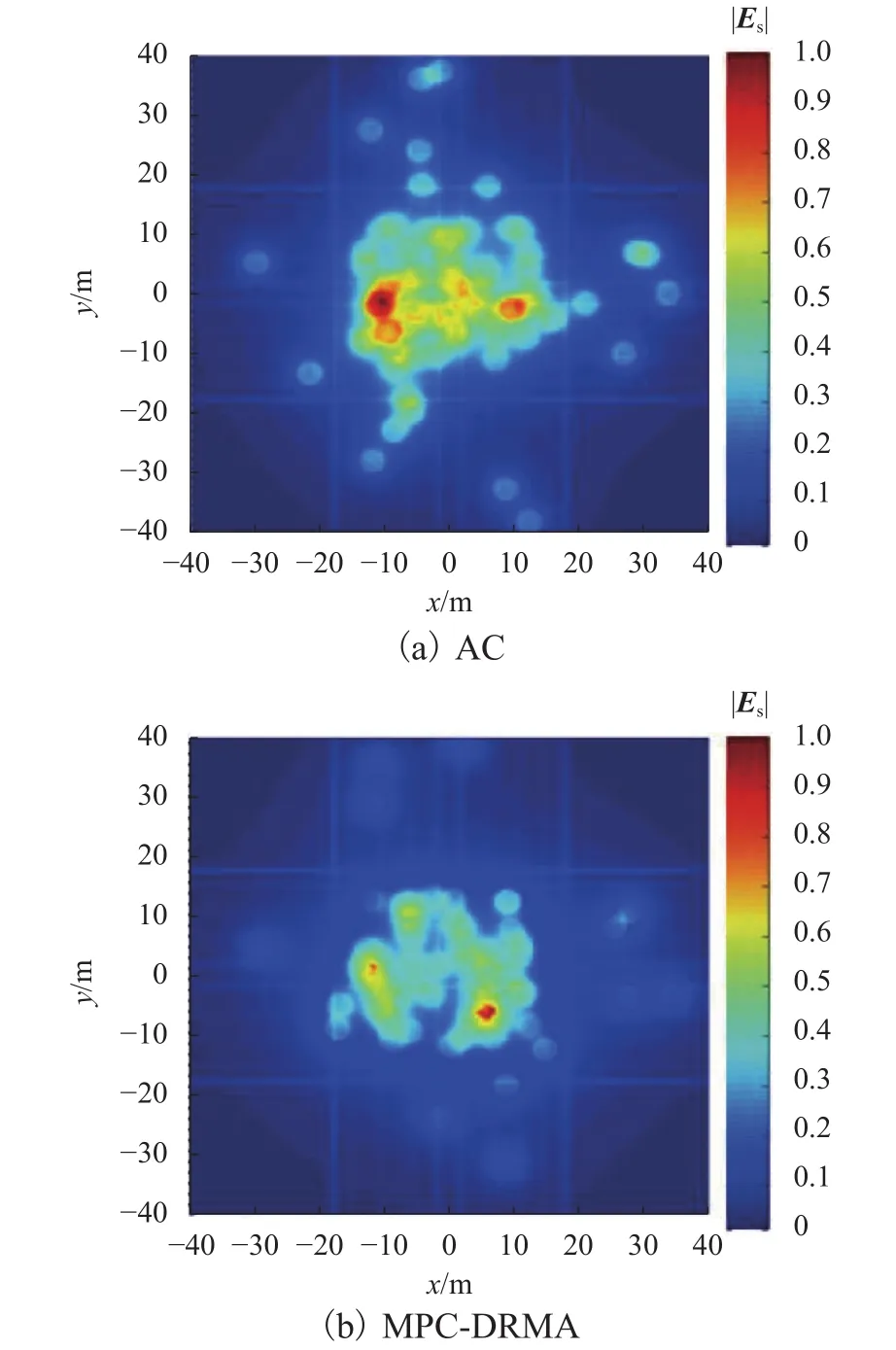
图6 车辆冲突场强分布二维图Fig.6 Two-dimensional diagram of field intensity distribution for vehicle conflict

3.2.3 道路拥堵水平的影响分析

MPC-DRMA算法对道路拥堵水平的影响如图7所示.由图可以得出，不同程度的道路负载对算法评价指标影响较大.针对总的延误时间指标，在所有交通条件下，MPC-DRMA算法收益均维持在80%以上.在VCR ＞ 1.0时，行程时间和通行能力的收益率得到明显改善.若交通状况处于过饱和状态，比如VCR ＞ 1.1，行程时间和通行能力改善明显.当交通状况处于流畅状态，比如VCR ≤ 0.9时，系统性能只是略有提升.当VCR ≤ 0.5时，行程时间和通行能力的变化不够明显，而在VCR ＞ 0.7时，提升效果则相对显著.在交叉口负载处于临界饱和及过饱和状态时，对于冲突次数的缓解非常明显，VCR =1.0时达到最大值，而后随着交通负载的增加，算法改善幅度趋于下降.

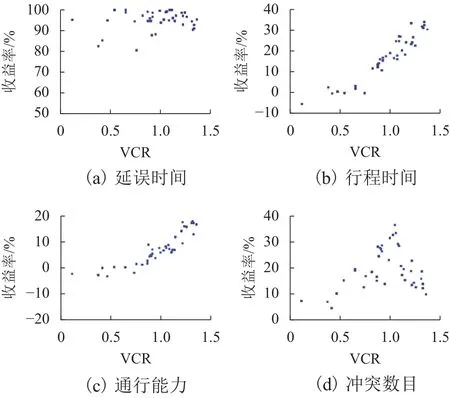
图7 不同拥堵条件增益情况Fig.7 Gains under different congestion conditions

不拥堵情况下，当VCR ＜ 0.8时，道路车辆数量相对偏少，车辆可以维持较长时间自由流动速度行驶.在AC模式下，在信号灯转变为红色时，车辆必须要在停止线外停车等待.而在MPC-DRMA算法控制下，车辆能够以最优速度快速通过交叉路口，避免了在停止线处等待的情况发生.进一步，如果自由流动速度大于最优速度，MPC-DRMA算法车辆可通行时间就会远高于AC模式，特别是在交通状况非常通畅时，图5（b）中也证明了这一结论.但是，通过改变车辆具体的控制变量的数值，如车速速度、时间间隔以及加减速度等限制，也能够在一定程度上优化交通状况通畅时车辆所消耗的行程时间.

4 通信性能对控制算法的影响

本文搭建了耦合式仿真试验平台，模拟非理想通信环境，如图8所示.

图8 耦合式仿真试验平台Fig.8 Coupling simulation test platform

为了准确度量通信性能的影响，选择平均端到端延迟（average end to end delay，Avdelay）[22]、数据包投递率（packet delivery rate，PDR）[23]作为网络性能的评价指标.同时，选取平均车速和冲突数目作为控制算法评价指标，用于评估通信性能对控制算法的具体影响，仿真结果如图9、10所示.

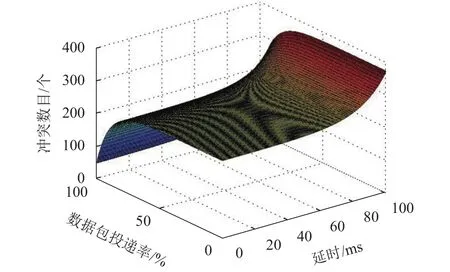
图9 冲突数目与数据包投递率、平均端到端延迟的关系Fig.9 Relationship between number of conflicts,PDR and Avdelay

由图9可知：在数据包投递率较大时，冲突数目明显处于较好状态，冲突的风险很低；当网络带宽长时间处于重度负荷状态，数据传输的质量无法得到保证，频繁出现数据丢包等问题，直接导致算法的结果不够理想，冲突数量也随之显著增加；若通信环境理想，不存在通信延时，车辆冲突数目也相对比较少；但是随着通信时间的延迟程度的增长，尤其是在达到70 ms以后，冲突数目也随之上升.

由图10可知：当通信延时持续增加，平均车速呈现出逐渐降低的趋势，一旦数据传输的通信延时超过80 ms，车速显著下降；若情况继续恶化，延时在超过100 ms后，车辆被迫停车（车速为0），说明此刻算法已经失效，无法继续协调车辆通行；在数据包投递率逐渐改善后，车速也相应开始增加，数据丢包不断加重；当丢包率接近35%时，平均车速快速下降，MPC-DRMA算法的性能降低，协调的效果不够理想.

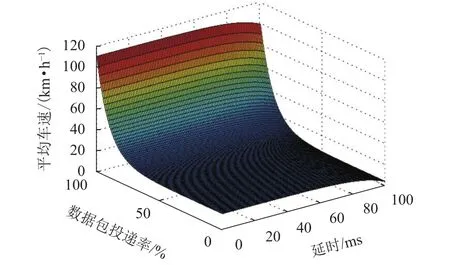
图10 平均车速与数据包投递率、平均端到端延迟的关系Fig.10 Relationship between average speed,PDR and Avdelay

5 结束语

本文考虑了网联环境无信号交叉口内车辆通行的特点，提出了基于MPC-DRMA算法的一种无信号交叉路口车辆协同控制方法.搭建了基于VISSIM、NS3和MATLAB的联合仿真平台，对本文算法进行验证，结果表明：

1） 本文所提算法使交叉口冲突的数目大幅减少，在车辆驶过交叉路口的过程中，碰撞风险也显著降低.在理想网联自动驾驶环境下，车辆行车风险的强度、分布密度都有显著的降低，车辆风险场强的峰值有所减小，并且缩小了车辆行车风险的分布区域范围.针对总的延误时间指标，在所有交通条件下，MPC-DRMA算法均要好于传统的AC系统，改善幅度一直维持在80%以上.在VCR ＞ 1.0时，收益甚至超过了90%.

2） 在非理想通信环境下，本文所提算法在数据包投递率较大时，冲突数目明显处于较好状态，冲突的风险很低.在通信延迟低于100 ms，数据丢包在35%之内算法仍效果较好.

下一步研究工作是将本文所提算法的模型结构及参数展开优化.同时对非理想环境下的无信号交叉口车辆系统控制进行深入研究，尤其是对网络协议和拓扑等方面仍需进行深入探究.