考虑源网荷不确定性的电力系统概率暂态稳定预防控制

王卫， 李雅晗， 王腾飞， 宫成， 夏世威*， 张东英

(1.国网北京市电力公司， 北京 100031； 2.华北电力大学电气与电子工程学院， 北京 102206)

“30-60”双碳目标必将加快风电、光伏等新能源的跨越式增长，促进中国以新能源为主体的新型电力系统快速发展[1]。但新能源发电一般具有间歇性和波动性，其大规模并网运行会为系统运行引入不确定因素，对系统的安全稳定带来挑战，如何有效分析新能源功率波动对电力系统安全稳定运行的影响并提出相应的预防控制措施有重要意义。

已有学者建立了不确定负荷需求或新能源发电概率模型，量化母线电压、线路潮流等相关输出量的均值和标准差，采用概率潮流[2-3]或概率最优潮流[4]进行了新能源电力系统概率静态安全分析。而关于新能源功率波动对电力系统概率暂态安全影响的研究相对较少，已有研究多数基于蒙特卡罗(Monte Carlo, MC)方法进行了电力系统概率暂态稳定(probabilistic transient stability, PTS)分析[5-6]。文献[7]采用MC方法并利用EMTP仿真软件评估了考虑双质量块风机模型的风电场概率暂态稳定水平。MC方法对所有样本点逐一进行暂态稳定分析，再统计所有样本点下的系统概率暂态稳定指标以评估系统概率稳定水平。可见，MC方法简单直观，但将其运用在PTS分析方面耗时较长。文献[8]提出了基于机器学习的大规模交直流电网动态安全风险智能评估模型，通过离线训练的方式对未来不确定场景和预想事故进行功角稳定、电压安全与频率安全的动态安全在线评估。文献[9]建立了基于实用动态安全域的概率暂态稳定指标，提出了基于Nataf逆变换和Gauss-Hermite积分的多点估计法快速准确评估了电力系统概率暂态稳定。文献[10]针对高比例新能源电力系统，采用层次聚类方法对系统的概率暂态稳定性进行了准确评估。上诉文献均聚焦于概率暂态稳定评估，但对概率暂态稳定的高风险运行场景，如何进一步提高含间歇性新能源的电力系统概率暂态稳定研究有待加强。

针对以上问题，提出了概率暂态稳定预防控制模型(preventive control with probabilistic transient stability, PC-PTS)以提高系统概率暂态稳定水平。该模型将考虑风电功率多点随机耦合注入、节点负荷随机波动、故障类型和位置以及故障切除时间等不确定因素，并计及双馈风机(doubly fed induction generator，DFIG)的动态过程。考虑到PTS计算复杂且费时，求解含PTS过程的PC-PTS模型将带来更大计算量、更加耗时，因此提出了基于点估计(point estimation，PE)策略和粒子群优化(particle swarm optimization，PSO)的混合PSO-PE优化算法以快速有效求解PC-PTS模型，并通过New England 10机39节点系统仿真结果验证所提PC-PTS模型和PSO-PE方法的有效性。

1 概率暂态稳定预防控制模型

风电机组接入电网，由于风能天然具有波动性，导致风机输出功率亦具有随机波动性，此时电力系统中常规机组出力需要匹配改变，以保持系统总体功率平衡。对于暂态稳定而言，常规机组出力匹配风电功率波动便形成了不同初始工况，导致暂态稳定分析中微分代数方程的解不同，对应的电力系统概率暂态稳定水平不再是一个确定值，而是与风电功率波动密切相关的随机因变量，形成了电力系统的概率暂态稳定问题。考虑到：①电力系统中常规机组具有一定的变负荷能力，通过调整传统机组的出力可方便地改变系统初始运行点；②电力系统中的初始运行点不同，系统概率暂态稳定水平将不同，因此协调优化常规机组运行状态可为电力系统概率稳定预防控制提供有效手段。基于以上思想，提出计及DFIG动态过程和源网荷不确定性的PC-PTS预防控制模型及对应求解方法。

1.1 不确定变量的概率模型

为清晰展示PC-PTS预防控制模型，仅考虑负荷、风电功率、故障类型和位置，以及故障切除时间5种不确定变量。对其他不确定变量，如故障发生概率、重合闸操作成功率等可采用类似方法加以处理。

1.1.1 荷不确定性-节点负荷概率模型

节点注入负荷是电力系统运行中负荷侧的重要不确定变量之一，用正态分布来描述节点i的有功功率PDi[11]。

(1)

式(1)中：μp和σp分别为p节点有功功率的均值与方差。

对于多个节点负荷的耦合关系[12-13]，可采用负荷相关系数Cpd来描述。而对于节点的无功功率可基于有功功率按固定功率因数计算获得。

1.1.2 源不确定性-风电功率概率模型

以风电为代表考虑电源侧的不确定性，对于其他类型的新能源不确定性可类似考虑。风机的输入风速以广泛使用的Weibull函数描述为[14]

(2)

式(2)中：λ和k分别为形状和尺度系数；νw为风速。

各节点风电功率间的耦合性实质为多个风电场风速间的相关性，可通过风速相关系数Cv描述风速来刻画。风电功率的计算公式为

(3)

式(3)中：Prated为风机额定功率；νci、νrd和νct分别为切入风速、额定风速和切出风速。

1.1.3 网不确定性-故障类型、位置及故障切除时间概率模型

考虑的电网侧影响系统稳定性的重要不确定因素包括：故障类型、故障位置及故障切除时间。故障类型可由离散概率模型描述，一般可基于电力系统运行的历史数据统计分析得出。针对电网发生不同故障类型X的概率，表1给出了基于BC Hydro公司历史数据和电机与电子工程师学会(IEEE)对北美电力系统的统计结果，可见两者差别不大[15]，而采用IEEE的统计结果进行计算。

线路故障位置Y理论上为连续型随机变量。但为了研究方便，一般将线路故障位置概率分布离散化：将线路分成若干部分，每一部分用一个典型位置点代替，并且假设线路各部分发生故障概率和其长度成正比。采用文献[16]中的线路故障位置概率分布值，如表2所示。

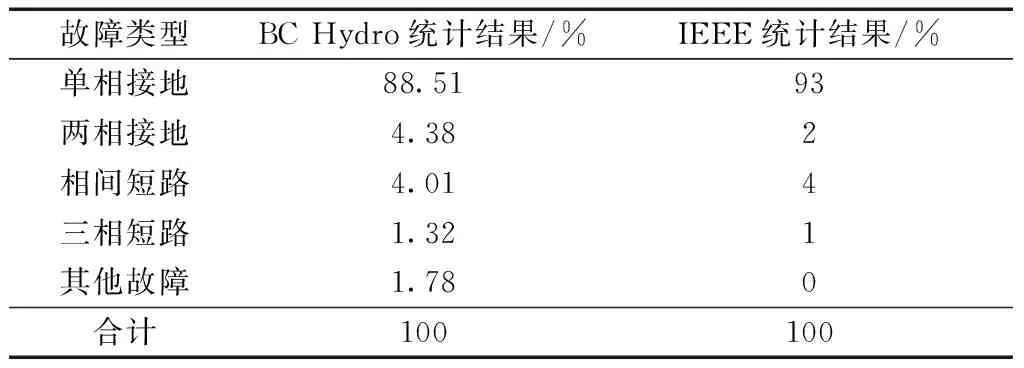
表1 不同故障类型X的概率值Table 1 Probabilities of different fault types X

表2 故障位置Y的概率值Table 2 Probabilities of fault locations Y

另外，还考虑了故障切除时间这一连续型不确定随机因素对系统暂态稳定性的影响。故障切除时刻对应电网结构变化的分界点，当故障切除时间不同时，故障中网络及故障后网络持续时长会不同，将会影响电力系统的暂态稳定性。因此故障切除时间的不确定性也可反映电网侧的不确定性。由于继电保护及通信网络运行状况不同，故障切除时间tcl呈现一定的随机性，也是影响暂态稳定分析的重要不确定变量，一般可用正态分布来模拟[17]。

(4)

式(4)中：μt和σt分别为故障切除时间的均值和方差。

1.2 概率暂态稳定预防控制模型实例

基于机会约束优化理论来形成电力系统的概率暂态稳定预防控制模型：将最小化系统燃料费用的期望值作为目标函数；以系统功率平衡为等式约束条件，将电力网络节点电压越限概率、输电线路过负荷概率及机组无功出力越限概率小于工程要求阈值作为静态安全不等式约束条件；将描述风机和常规机组动态特性的微分代数方程作为暂态过程等式约束，以系统概率暂态稳定水平大于设定阈值作为概率稳定约束条件。模型具体如下。

1.2.1 目标函数

电力系统一般通过调节平衡节点的功率来保持整个系统功率平衡。考虑不确定风电功率及随机性负荷后，平衡节点的功率也具有不确定性。因此当以整个系统的机组费用为目标函数时，目标函数值也会是不确定量，以期望值表示为

(5)

式(5)中：FG为所有机组总费用；E为期望值计算；PGi为传统机组i的有功功率，其上下限约束为PGmin≤PGi≤PGmax;ai、bi、ci为机组费用系数。

1.2.2 潮流方程等式约束

静态等式约束包括潮流等式[式(6)]约束。

(6)

式(6)中:i=1,2,…,nb；nb为系统总节点数；PDi为节点有功负荷；QGi和QDi分别为机组i的无功功率和节点无功负荷；PWi和QWi分别为节点i处的风机有功和无功功率；Gij和Bij为支路ij的导纳；Vi和Vj分别为节点i和节点j的电压幅值；θij为节点i和节点j的电压相角差。

上述功率平衡方程需在暂态稳定分析初始化和时域仿真过程中始终满足。

1.2.3 静态安全不等式概率约束

电力系统节点电压越限概率、输电线路过负荷概率及机组无功出力越限概率约束可表述为

P{QGimin≤QGi≤QGimax}>βQ，i=1,2,…,nG

(7)

P{Vimin≤Vi≤Vimax}>βV，i=1,2,…,nb

(8)

P{Sli≤Slimax}>βs，i=1,2,…,nl

(9)

式中：QGimin、QGi、QGimax分别为机组无功功率、无功功率的最小值和最大值；nl为线路总数；Sli为第i条线路的视在功率；βQ、βV和βS为静态安全的概率阈值。

式(7)～式(9)所示的概率不等式约束分别保证机组无功功率、节点电压幅值和线路输送功率以一定的风险水平维持在正常运行范围内。

1.2.4 暂态过程等式约束

PC-PTS模型需要考虑传统机组和风电机组的暂态过程。暂态稳定分析中，采用四阶模型来刻画机组动态特性[18]；调速器采用PSASP7型调速器模型[19]；励磁系统采用常见的IEEE 1型[20]。风机采用双质量块动态模型如式(10)、式(11)所示，结构如图1[21]所示。

(10)

(11)

式中：ωt、ωr和ωb分别为风机转速、发电机转速及系统同步转速；θtw为扭转角，rad；Ktw为刚度系数，p.u./rad；Dtw为刚度系数及阻尼系数；Ht为风机惯性常数；Pm为风能转化的机械能。

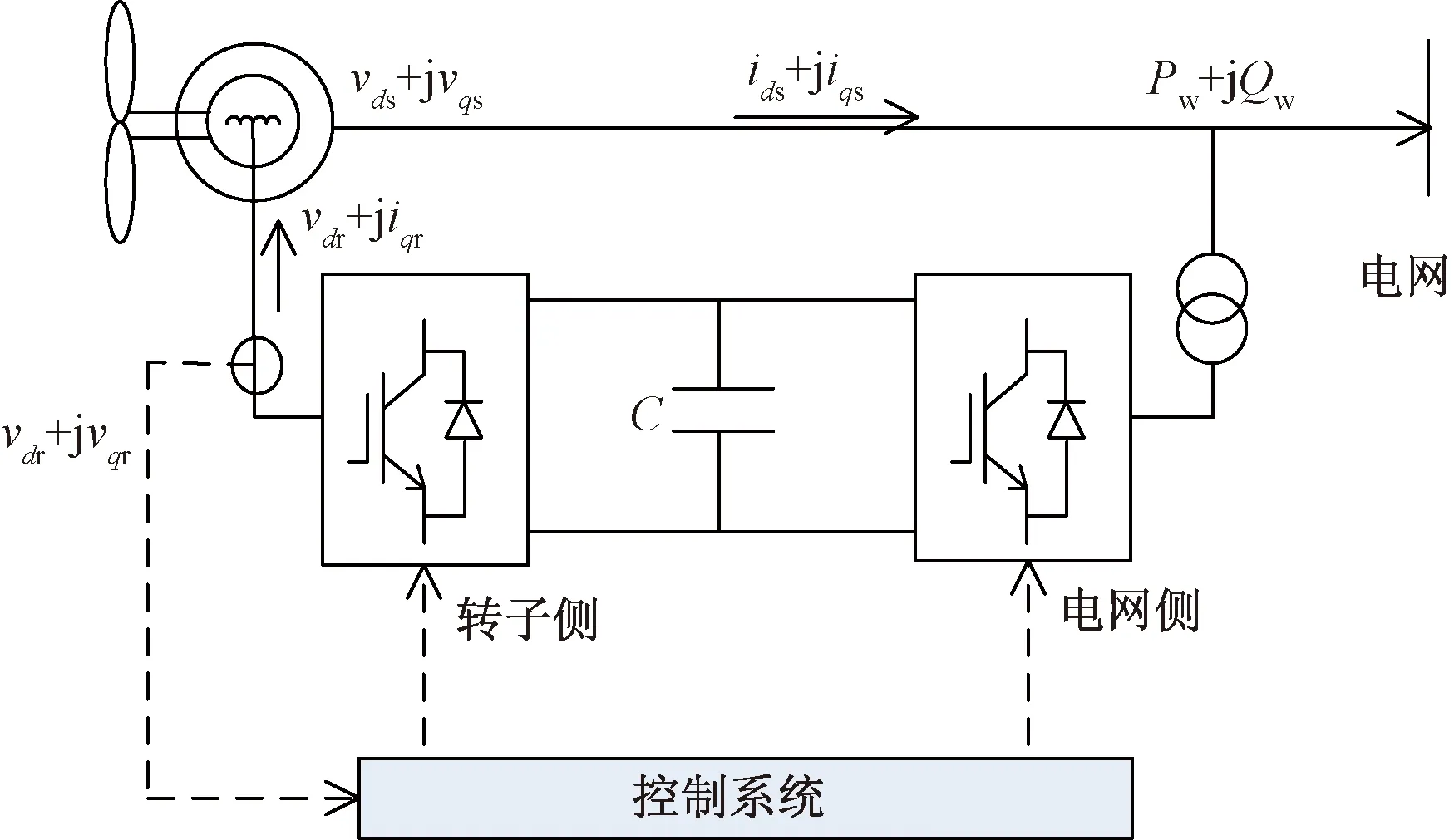
C为电容图1 DFIG结构图Fig.1 DFIG structure

忽略转子电流及直流电容的动态过程，双馈风机的模型可描述为[21]

(12)

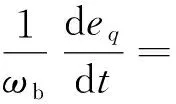
(13)

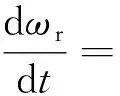
(edids+eqiqs)]

(14)

(15)

(16)

Pw=vdsids+vqsiqs-vdridr-vqriqr

(17)

Qw=vqsids-vdsiqs

(18)

式中：ed和eq分别为内电势d、q分量；Pw和Qw分别为双馈风机输出有功和无功功率；Hg为风机惯性时间常数；s和ωs为转差率和同步转速；rs为转子电阻；vqs、vds、iqs、ids分别为风机定子侧交、直轴电压和交、直轴电流；vqr、vdr、iqr、idr分别为风机转子侧交、直轴电压和交、直轴电流；Xeff和X′为风机等效开路和短路电抗；Lr和Lm分别为转子自感和互感；T0为暂态开路时间常数。

对于风机的端电压和有功功率采用磁链幅值相角控制(flux magnitude angle control，FMAC)控制策略[21]。

1.2.5 概率暂态稳定裕度约束

集成扩展等面积(integrated extended equal area criterion，IEEAC)法是电力系统暂态稳定分析常用工具之一，并已在中国多个区域电网实际应用[20-22]。该方法将积分空间和观测空间分开处理：①在积分空间：IEEAC法对多机转角在Rn空间中进行积分，保证了所有复杂情形下的多机轨迹都能体现出来；②在观测空间：IEEAC法选择和积分步长相同的映射步长，对多机系统的轨迹进行映射，定量计算暂态稳定裕度。IEEAC方法的适用性和精度由①来保证，系统的量化分析由②进行，其在计算速度和精度以及模型适应性等方面都具有优秀表现[22-25]。

将采用IEEAC方法计算暂态稳定裕度η，其可由减速面积Adec与加速面积Aacc之差确定，即[22-25]。

η=Adec-Aacc

(19)

不稳定情形下，同步机等值电磁功率与机械功率在不稳定平衡点处满足：

(20)

式(20)中：PmE、PeE分别为IEEAC方法单机映射后的等值机械功率与电磁功率；tu为到达不稳定平衡点时刻；Pa(tu)为tu时刻不平衡功率。

系统稳定裕度计算公式为

(21)

式(21)中：ME和ωE(tu)分别为IEEAC方法单机映射后的等值转动惯量及不平衡点处等值角速度。

稳定情形下，系统在到达不稳定平衡点前已经回摆。记最大回摆角为δr，则最大回摆角处应满足：

(22)

式(22)中：tr为最大回摆角时刻；Pa(tr)及ω(tr)分别为最大回摆角时刻的不平衡功率及等值角速度。

系统对应的稳定裕度计算公式为

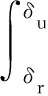
(23)

式(23)中：δu为持续故障法确定的不稳定平衡点。

基于上述多机电力系统暂态稳定裕度计算方法，容易评价系统在某初始运行状态下的系统暂态稳定性。设线路可能发生的故障类型有nx种，离散后的可能故障位置有ny个，进一步结合全概率公式[式(24)]可计算概率暂态稳定概率为P(I),因此预防控制模型概率暂态稳定约束条件为

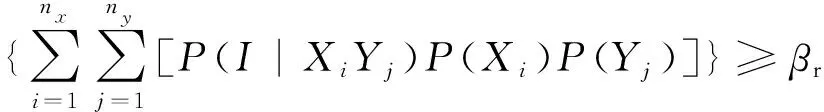
(24)

式(24)中：βr为概率暂态稳定阈值；Xi和Yj分别为第i种故障类型和第j个故障点；P(Xi)和P(Yj)分别为故障类型Xi及故障位置Yj发生故障的概率；P(I|XiYj)为线路在位置Yj发生故障类型Xi时，系统暂态稳定的概率。

由于P(Xi)和P(Yj)易从表1及表2获得，因此式(24)的量化关键在如何快速有效地计算条件概率P(I|XiYj)，即在故障位置Yj发生类型Xi的情形下，如何快速有效计算其他3种连续型不确定随机因素(包括随机波动节点负荷、多点耦合的风电注入功率及不确定的故障切除时间)影响下的系统概率暂态稳定水平。

2 PC-TSC模型的PSO-PE求解方法

2.1 基于Cholesky的点估计法

PE是处理概率问题的有效方法之一。与MC法需要大量样本相比，PE法通过少数样本便可计算得到随机因变量的各阶矩，尤其是2m+1 PE法(m为不确定变量的维数)以相对较低的计算量提供了令人满意的精度[26]。因此将引入2m+1 PE法并结合Cholesky分解来处理PC-PTS模型中的耦合连续型不确定变量。

在PC-PTS模型中，连续型不确定变量包括随机负荷、风电波动功率和正态分布的故障切除时间。将以上3种类型的不确定变量表示为m维不确定向量(z1,z2, …,zl, …,zm)，基于2m+1 PE法可生成2m+1个典型向量值，具体步骤如下[27]。

步骤1对不确定元素zl生成3个典型值：用3个位置zl,k(k=1,2,3)替换不确定元素zl，而剩余的m-1个不确定元素固定为平均值μz1,μz2, …,μz(l-1),μz(l+1), …,μzm,从而生成3个典型向量(μz1,μz2, …,μz(l-1),zl,k,μz(l+1), …,μzm)，其中k=1,2,3。

步骤2对不确定向量(z1,z2,…,zl, …,zm)中的每个元素重复步骤1)，因此对m维的不确定向量，将共产生3m个典型向量(μz1,μz2, …,μz(l-1),zl,k,μz(l+1),…,μzm)，其中，k=1,2,3;l=1,2,…，m。

位置参数zl,k的计算公式为

zl,k=μzl+εl,kσzl，k=1,2,3

(25)

式(25)中：ε1,k为标准位置；μzl和σzl分别为变量zl的均值和标准差。

标准位置εl,k和权重ωl,k可由式(26)、式(27)获得[25]。

(26)

(27)

式中：λl,3和λl,4为变量zl的偏度和峰度。

式(26)中，由于ε1,3=0致使z1,3=μzl，因此m个典型向量均相同为(μz1,μz2, …,μz(l-1),μz(l+1), …,μzm)，进而典型向量总个数将从3m减少到2m+1。

通过式(25)～式(27)原始不确定向量(z1,z2, …,zl, …,zm)的不确定性可被2m+1个确定向量等效表征，进而逐次进行常规潮流和暂态稳定分析，得到输出变量值S(如节点电压、线路潮流和暂态稳定裕度η等)。假设输出因变量值Sl,k与典型向量(μz1,μz2, …,μz(l-1),zl,k,μz(l+1), …,μzm)间的关系用函数F表示为

Sl,k=F(μz1,μz2,…,μz(l-1),zl,k,μz(l+1),…,μzm)

(28)

通过Sl,k和式(27)中权重ωl,k可以计算输出变量S的j阶原点矩mj[28]，计算公式为

(29)

基于式(29)计算各阶原点矩后，输出变量的概率累计分布函数(cumulative distribution function, CDF)可由Gram-Charlier级数估算得到，详细过程参见文献[28]。

由于考虑了负荷和风电功率的耦合特性，需采用Cholesky分解方法对PC-PTS中不确定变量的相关性进行处理，具体如下：首先通过Cholesky分解将相关输入变量转换为不相关变量；然后利用2m+1 PE方法获得不相关变量的2m+1组向量并基于Cholesky矩阵求逆，即可生成原始相关输入变量的典型向量，再进一步进行确定性暂态稳定分析，计算得到输出变量的各阶原点矩，并利用Gram-Charlier级数计算输出变量的CDF，包括节点电压越限概率、输电线路过负荷概率、机组无功出力越限概率以及系统暂态稳定条件概率P(I|XiYj)。

2.2 粒子群优化(PSO)方法

所提的预防控制模型含有复杂、高度非线性的概率约束条件如式(7)～式(9)及式(24)，模型本质上属于机会约束优化问题，一般不易通过传统的数学规划方法求解，将引入PSO求解该模型。PSO算法是一种基于发现-搜索模型的全局优化方法，具有模型适应性好，全局寻优能力强，优化过程收敛速度快的优势。采用文献[29]的增强型粒子群方法(enhanced particle swarm optimization, EPSO)来求解PC-PTS模型。

由于模型中的有功、无功功率平衡约束[式(6)]和微分代数方程[式(10)～式(18)]已经通过2m+1 PE法中的确定性潮流和暂态稳定仿真间接处理，因此求解模型仅需有效处理概率不等式约束[式(7)～式(9)]和式(24)。这里采用罚函数法来处理这些概率约束形成无约束优化问题[式(30)]，以方便使用EPSO方法进行求解。

minF(x,u)=FG+prmax[0,βr-P(I)]+

P{Vimin≤Vi≤Vimax})+

(30)

式(30)中：pf和pr为式(7)～式(9)和式(24)概率约束的惩罚因子；u为待优化控制变量。

2.3 求解PC-PTS模型的EPSO-PE综合优化方法

概率暂态稳定预防控制模型本质上是含有暂态稳定分析和机会约束的最优潮流模型，求解难点是如何有效地处理与随机变量相关的机会约束条件。融合2m+1点估计法、Gram Charlie级数理论[28]以及PSO优化算法，从而形成求解PC-PTS模型的PSO-PE综合求解方法，步骤如图2所示。

图2 求解PC-PTS模型的EPSO-PE法流程图Fig.2 Flowchart of EPSO-PE to solve PC-PTS

步骤1输入系统数据，采用基于Cholesky分解的2m+1 PE法生成PC-PTS模型中连续型不确定变量的典型向量，并依据表1、表2形成故障类型及位置的离散概率值；设定PSO优化算法参数，随机初始化PSO粒子位置。

步骤2基于2m+1次的暂态稳定分析结果，据Gram Charlie级数理论计算式(7)～式(9)中变量、式(24)中条件概率P(I|XiYj)以及式(5)中燃料成本的累积概率分布函数(CDF)，然后由相应CDF评估对应概率约束和期望燃料成本；同时基于全概率式(24)计算系统暂态稳定概率值P(I)。

步骤3通过式(30)评估每个粒子的适应度。

步骤4记录所有粒子中的最佳适应度，同时判断是否达到最大迭代次数：若达到，则输出PCPTS模型的最优解；否则，增加控制变量的迭代次数并更新PSO粒子位置，返回步骤2。

3 仿真结果

以图3所示10机39节点系统为例，验证PCPTS模型的合理性[30]。该系统中含有4个风电场(以W表示)，每个风电场包含100台额定功率为2MW的双馈风机，参数为：Ktw=0.6 p.u./rad，Dtw=0.45 及Ht=3.8 s。常规机组采用四阶模型，配置IEEE 1型励磁系统及PSASP7型调速器。支路15-16发生故障，tcl时刻切除故障。系统节点电压取值范围[0.97, 1.06]，所有概率约束阈值(即βQ、βV、βS和βr)取值为0.95。系统的不确定条件设置如下。

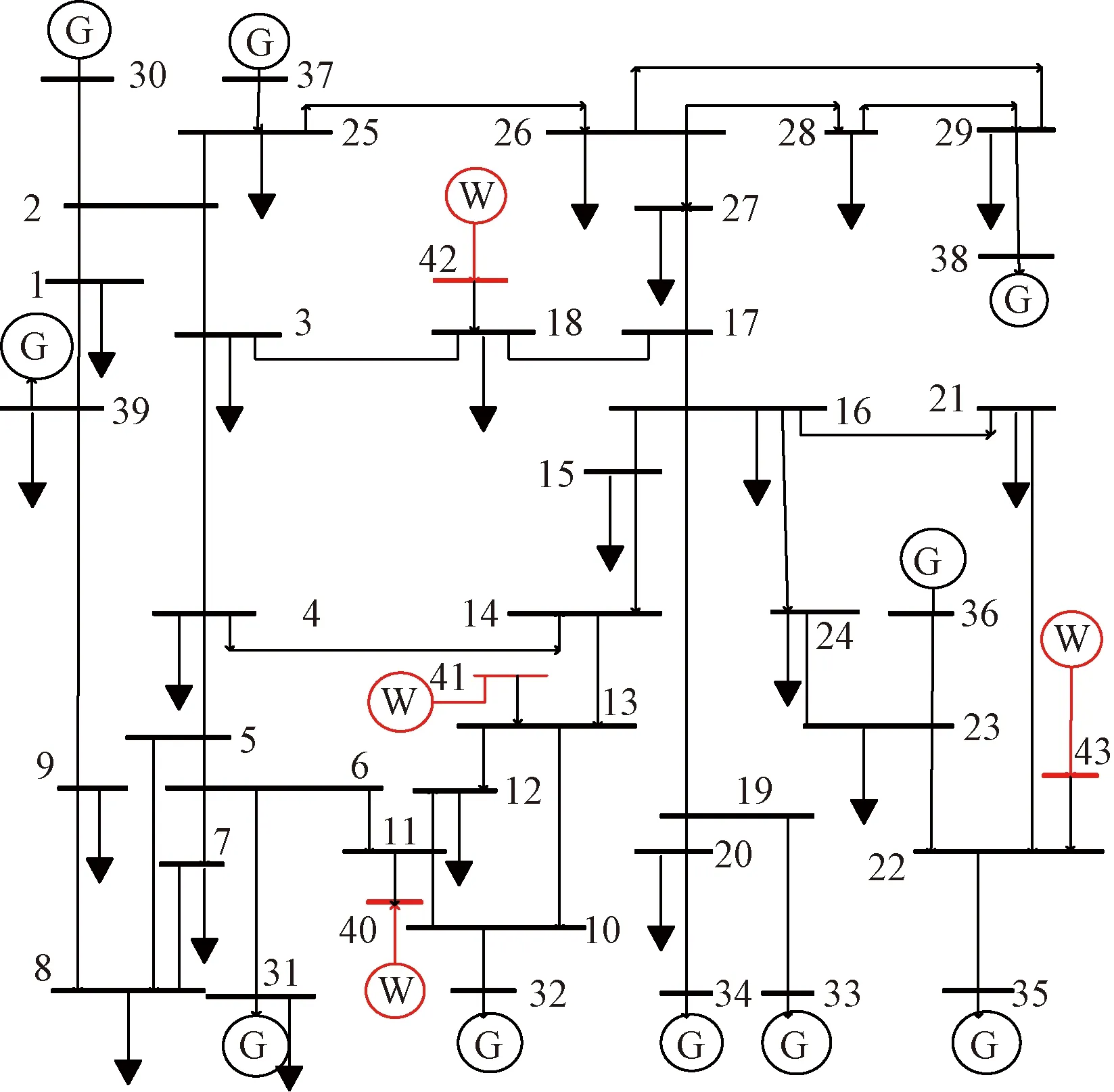
W为风电场；G为同步机组图3 含多点耦合风电的10机39节点系统图Fig.3 10-generator 39-bus system with multi-point coupled wind power

(1)节点负荷功率为正态分布，均值为系统标准数据，方差为均值的10%；21个相互耦合的节点负荷相关系数为0.15。

(2)风速的形状系数和尺度系数分别为：λ=2和k=12，4个耦合的风电场之间的相关系数为0.3，风机的切入、切出及额定风速分别为νci=3 m/s,νct=25 m/s和νrd=12 m/s。

(3)支路15-16发生故障，故障类型及具体故障位置的概率值采用表1、表2中的数据；另外故障切除时间为正态分布，均值为μt=350 ms，标准差为σt=0.1μt。

3.1 实施预防控制前的系统指标

当10机39节点系统的机组出力为优化前的标准数据时，系统整体的费用期望值为57 486.97$/h，如表3所示。在此情形下，系统其他概率指标无法满足要求。如以故障类型Xi为三相短路、故障位置Yj靠近15节点为例：①节点4电压幅值在区间[0.97, 1.06]的概率只有0.19，低于要求的概率水平0.95；②而支路6-11传输功率不越限(小于传输容量极限为6 p.u.)的概率只有0.5；③如图4所示，系统暂态稳定条件概率P(I|XiYj)为0.62(稳定裕度大于零部分)。再基于表1、表2中所有可能故障类型及故障位置Yj的离散概率值，依据全概率[式(24)]可计算得到系统暂态稳定概率值为0.563 8，表明系统失去暂态稳定的概率高达0.436 2，因此无法满足概率暂态稳定水平大于0.95的指标要求。

3.2 实施预防控制后的系统指标

当实施预防控制模型后，采用PSO-PE综合方法求解的系统期望费用为58 910.48 $/h(表3)。与实施预防控制前相比，系统费用期望值略有增加，但所有概率约束条件均得到满足。如故障类型Xi为三相短路、故障位置Yj靠近15节点时，系统暂态稳定条件概率P(I|XiYj)接近1(图5)，相比于预防控制前，P(I|XiYj)明显增大；再综合表1、表2所有故障类型及故障位置，基于式(24)可计算得到系统的暂态稳定概率为0.978 6，满足概率暂态稳定水平0.95的指标要求。

表3 暂态稳定预防控制前后机组功率及指标Table 3 Power output and security index before and after PC-PTS control

图4 预防控制前系统暂态稳定概率Fig.4 CDF of transient stability margin before PC-PTS

图5 预防控制后系统的暂态稳定概率Fig.5 CDF of transient stability margin after PC-PTS

当系统概率稳定水平βQ、βV、βS和βr变化时，系统的费用期望值也随之变化。如表4所示，当系统的概率稳定水平较低时，系统期望费用值较低；随着概率稳定水平的提高，系统需牺牲一定的经济性来提高概率安全水平。

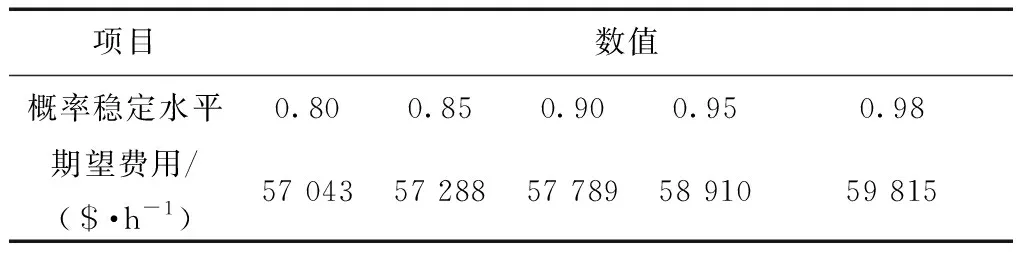
表4 不同稳定水平下的系统期望费用Table 4 Fuel cost expectation at different security level

4 结论

针对新能源功率波动带来的电力系统安全问题，从预防控制角度提出了基于机会约束的电力系统概率暂态稳定预防控制模型，以提高新能源电力系统的概率暂态稳定水平。模型综合考虑了源侧的风电功率随机耦合注入、网侧的故障类型、故障位置和故障切除时间的不确定性，以及负荷侧的节点负荷波动性。进一步提出了基于点估计法和粒子群优化算法的PSO-PE综合求解方法，快速有效地求解了概率暂态稳定预防控制模型。改进的New England39节点系统仿真结果表明：所提出的PC-PTS模型合理，PSO-PE方法可快速求解该模型，两者结合可有效提高考虑源网荷不确定性的电力系统概率暂态稳定性，增强系统运行安全水平。