基于新样本的滑坡坝溃决洪峰流量预测模型修正与对比

阮合春， 陈华勇*， 李霄， 俞昀晗， 李鑫

(1.中国科学院山地灾害与地表过程重点实验室, 成都 610041; 2.中国科学院水利部成都山地灾害与环境研究所， 成都 610041； 3.中国科学院大学， 北京 100000； 4.开远市水利勘测设计队， 红河 661699)

地震或强降雨能够引发大量滑坡，或产生诸多潜在滑坡体；一旦滑坡体启动，极易堵断其运动方向上的河流，迅速雍高上游水位，形成具有重大潜在威胁的堰塞坝[1-2]；因堰塞坝结构松散，未经人工设计，通常在很短时间内就发生漫顶溢流溃决，形成具有强大破坏力的溃决洪水[3-4]。如2018年10月10日和11月3日，西藏江达县与四川白玉县的交界处的白格村连续发生了两次滑坡堵江事件，形成的堰塞坝均在不久后发生了漫顶溢流溃决，形成的溃决流量分别达到10 000、33 900 m3/s，给下游造成了严重损失[5]。

溃决洪峰流量作为溃坝问题中的重要参数，是进行堰塞坝风险评估及下游洪水演进模拟的前提条件，其大小直接决定了下游的灾害程度[6-8]。因此，在滑坡坝形成后，准确快速得到其溃决洪峰流量显得尤为重要。

因堰塞坝形成后难以在短时间内获取溃坝动力学模型计算所需的完整参数[9]，基于历史统计案例得到的参数模型得到了广泛应用。Peng等[10]基于45组滑坡坝历史案例，构建了一个可考虑坝体易蚀性的溃决洪峰流量预测模型，并与部分常用的参数模型进行对比验证。Zhou等[11]汇总了目前已有的溃坝洪峰流量预测经验模型，但并未对模型进一步的分析对比验证。Hakimzadeh等[12]基于37个滑坡坝溃决案例，构建了一个考虑坝高和库容的溃决洪峰计算参数经验式，并采用均方根误差(mean square error，RMSE)和效率系数E两个指标分析了公式的合理性。Ruan等[13]借鉴人工土石坝的半理论模型，通过历史滑坡坝案例构建了一个滑坡坝的半理论半经验模型，并将其与已有的经验参数模型进行对比，并表明已有的经验参数模型对新样本的预测结果存在较大误差。从陈生水等[14]、Zhou等[11]、Ruan等[13]汇总的滑坡坝溃决洪峰流量经验计算式中可以看出，这些公式在构建时所采用的案例数及溃决洪峰流量区间十分有限，对新样本的预测结果存在较大的不确定性；此外，因坝体溃决时，溃口水流为强非恒定流，上游水位变化复杂，难以定量描述，溃决过程中水位下降的高度d及水体的势能PE难以事先得到，故含有该参数的公式仍具有较大局限性。因此，基于新溃坝案例数据库，修正已有的滑坡坝溃决洪峰流量参数预测模型，为滑坡坝的防灾减灾及相关工程设计提供重要理论参考显得尤为重要。

为此，首先通过文献查阅，对滑坡坝溃决案例的数据库进行扩充，进而采用得到的新数据库对已有的经典滑坡坝溃决洪峰流量的预测模型进行修正，并对比了修正后各模型对新样本的预测效果，最后采用白格滑坡坝对修正后的模型进行应用对比。

1 滑坡坝溃决数据库

从表1[10，12，15-17]中可以看出，已有可用于滑坡坝溃决洪峰流量预测的数据库中的案例数十分有限，仅为45例。在广泛收集中外相关文献的基础上，获取了来自全球各地的67组滑坡坝溃决历史案例数据(表2[18-59])，其中有45例来自Peng等[10]的数据库中，但该数据库中未包含2012年至今的滑坡坝溃决案例。此外，本文数据库中最小的洪峰流量与已有数据库中最小的洪峰流量相同，均为1991年8月17日发生于新西兰的Unawaea滑坡坝，洪峰流量仅为250 m3/s；但本文数据库中最大的洪峰流量达到509 000 m3/s (1840年12月发生于巴基斯坦印度河流域的南迦帕尔巴特附近)，为已有数据库中最大溃决洪峰流量(2000年4月9日发生于西藏易贡藏布左岸的扎木弄沟，洪峰流量为124 000 m3/s)的4.1倍。表明该数据库已经包含了极为罕见(或极端)的情况，采用该数据库修正的模型更加稳定，适用范围更广。

坝体易蚀性是指坝体材料对水流侵蚀作用的抵抗能力，坝体易蚀性越高，坝体溃决速率越快，溃决流量越大，峰现时间越短。在Peng等[10]研究中，将搜集的45个滑坡坝溃决案例的坝体易蚀性划分为了高度易蚀性、中度易蚀性、低度易蚀性三类，分别用字母“H、M、L”表示，其划分标准则是借鉴Briaud[60]提出的土壤易蚀性的划分方法，即根据土壤侵蚀率和溃口流速或者水流剪切力的关系，将土壤的易蚀性划分为6种类型(非常高、高、中、低、非常低、无侵蚀)[60]。事实上，由于滑坡坝常发生于人烟稀少、交通不便的高山峡谷地区，且限于测试技术的限制，难以获取土壤侵蚀率和、溃口流速、水流剪切力等动力学参数；已有的大多数历史案例资料中，仅对坝体物质组成、形态特征等一些基本情况进行了简要介绍。因此，采用水动力学参数判断坝体易蚀性存在一定主观性[10]，且实用性不强。

参考Cui等[61]根据坝体颗粒组成划分堰塞湖危险性的方法，同样将滑坡坝易蚀性划分为高度易蚀性H、中度易蚀性M、低度易蚀性L三类，划分标准如表3所示。该方法在实际过程中，参数更容易获取，应用更加方便。

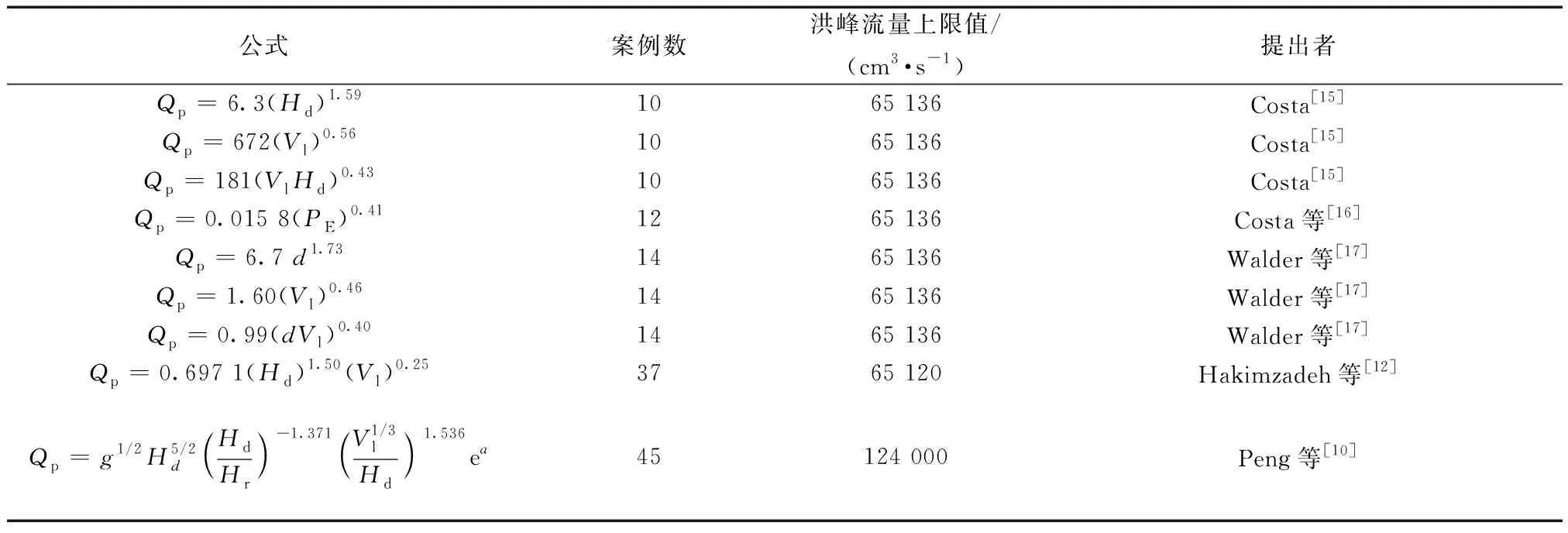
表1 滑坡堰塞坝溃决洪峰流量的经验模型Table 1 Empirical model of peak discharge caused by landslide dam failure

表2 全球滑坡堰塞坝溃决历史案例数据Table 2 Historical case data of global landslide dam failure

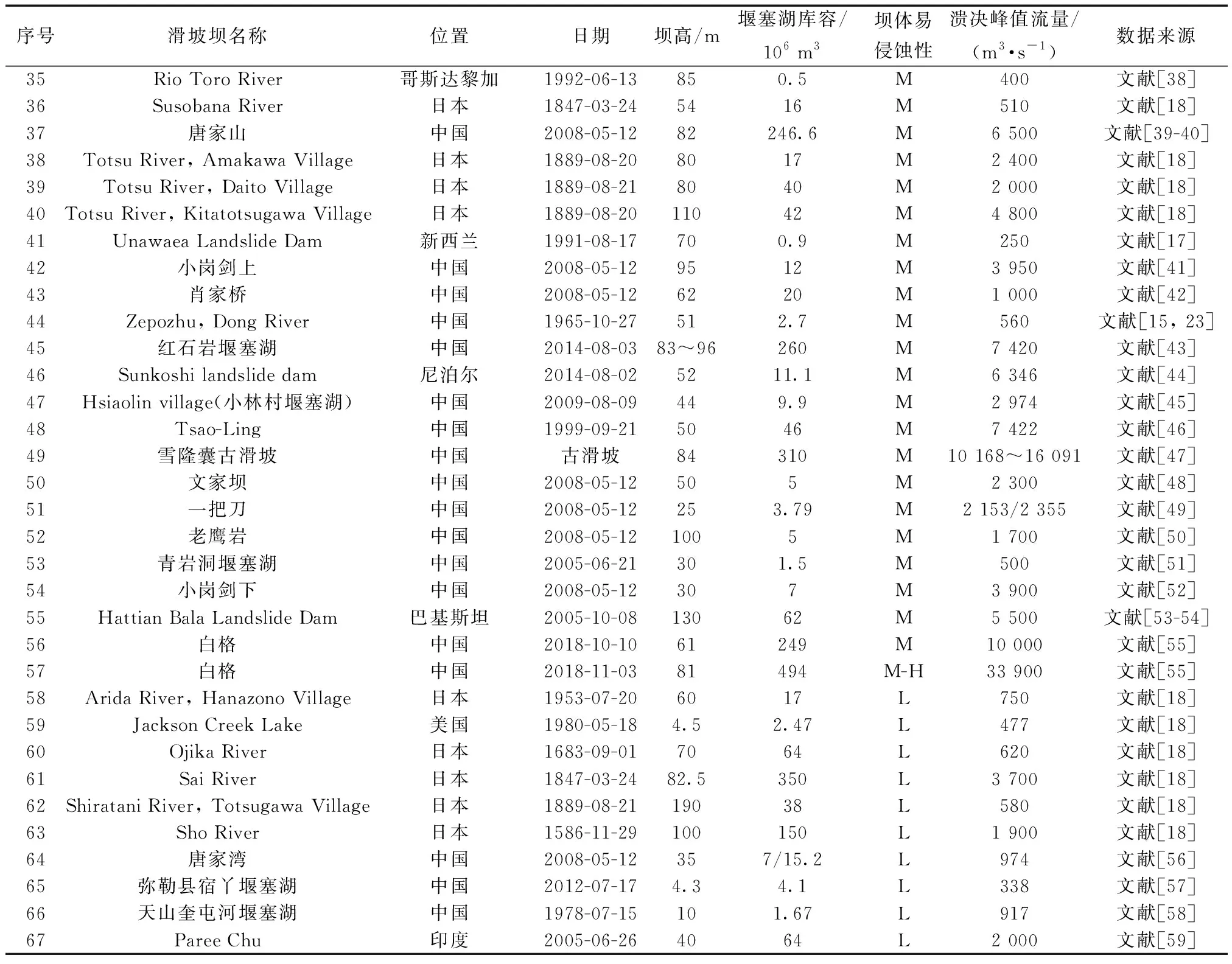
续表2

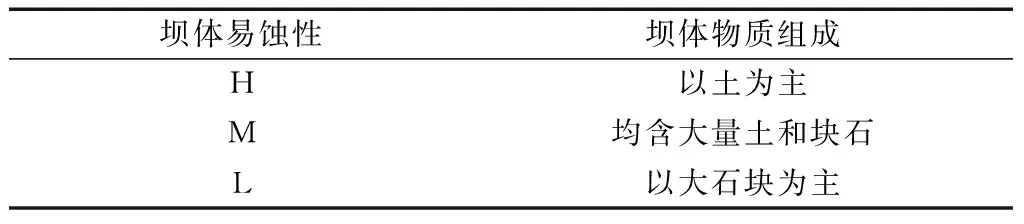
表3 堰塞坝易蚀性划分标准Table 3 Standard for classification of erodibility of landslide dams

图1 滑坡坝形态示意图Fig.1 Schematic geometry of landslide dams

2 模型的修正与对比

堰塞坝溃决是一个过坝强非恒定流与坝体复杂岩土体材料相互作用的复杂过程。一方面，过坝水流的动力条件(冲蚀能力)会直接影响溃口的侵蚀速率，进而改变泄流通道的大小，溃决流量也会随之变化；另一方面，坝体岩土体材料的性质直接决定了自身的抗冲蚀能力，进而改变过坝水流的水动力条件，比如坝体大颗粒的存在或黏粒含量的增加均会降低坝体侵蚀能力。因此，表1总结的诸多滑坡坝溃决洪峰流量预测模型中，溃决过程中水位下降的高度d及水体的势能PE难以准确描述和预测，不能事先得到，故在表1中含有参数d和PE的模型难以应用于实际堰塞坝溃决洪峰流量的预测中。基于此，经筛选后，仅针对表4中的模型进行修正。

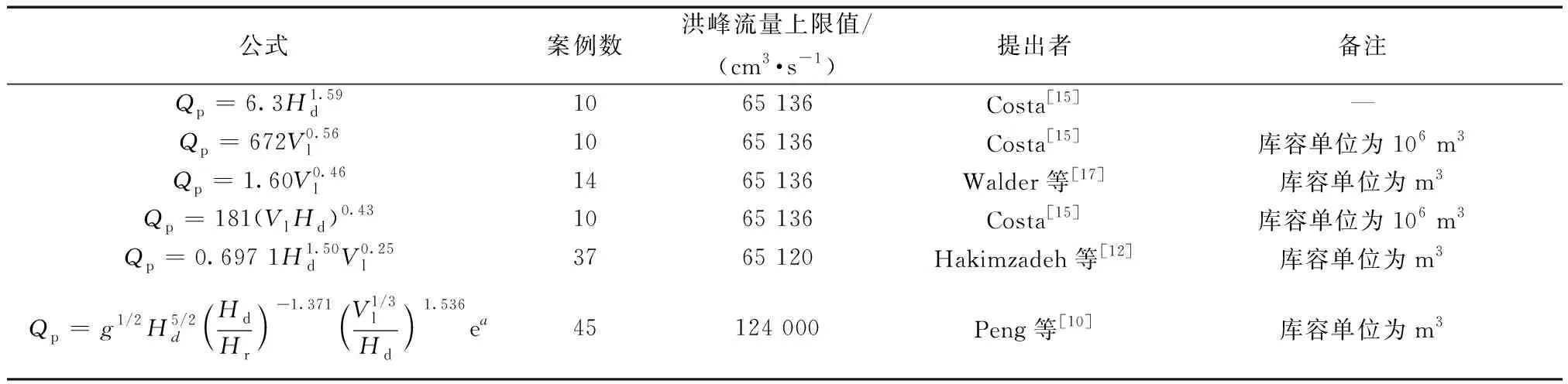
表4 用于修正的滑坡堰塞坝溃决洪峰流量经验模型Table 4 The empirical model of peak discharge caused by landslide dam failure for modification

基于表2中的67个滑坡坝溃决案例，对表4中的模型进行回归分析，得到各模型修正后的具体形式，并将修正结果点绘于图2～图4中。同时，为了进一步对比各模型修正前后的计算效果，采用RMSE和相关系数R2对各模型的计算效果进行度量。其中，RMSE对样本容量中的极值(最大值和最小值)最为敏感，可在一定程度上反映洪峰流量计算模型的整体精度，RMSE越小，模型计算效果越好；R2是用以反映变量之间相关关系密切程度或可靠性的统计指标，R2越大，模型计算效果越好，在确定修正模型的具体参数值时，选用的参考度量指标主要为相关系数R2。RMSE、R2的计算公式分别为

(1)

(2)

(3)

式中：Qcal,i为第i个滑坡坝溃坝案例的洪峰流量预测值，i=1,2,…,67)；Qoal,i为第i个滑坡溃坝案例的洪峰流量实测值(i=1,2,…,67)；N为滑坡坝溃坝案例的总数，N=67；Qobsm为洪峰流量实测值的平均值。

通过计算，得到了各模型修正前后的RMSE和R2，如表5所示。

从图2～图4及表5中可以看出，采用新样本修正后的滑坡坝溃决洪峰流量计算模型相较于原始模型的计算效果均有不同程度的提升：修正后的RMSE和R2较修正前均有所改善。但Costa[15]坝高Hd单参数模型[图2(a)]修正前后的R2仅分别为0.029 4、0.074 6，RMSE也基本不变，表明坝高与洪峰流量的相关性不明显；同时，对比Costa[15]库容Vl单参数模型和Walder等[17]库容Vl单参数模型(二者修正后的R2分别为0.831 4、0.972 7，RMSE分别降低13.87%、78.34%)可以看出，库容与坝高才存在良好的相关性，这一结论与实际情况基本吻合：滑坡坝在大江大河或沟道内均会发生，尤其在地质环境恶劣的高山峡谷地区更为频发，河道或沟道底床坡度从零度至几十度不等，该情况下，即使具有相同的坝高，在不同的底床坡度下，库容也会十分悬殊；根据水量平衡方程[式(4)]，同一坝高下，底床坡度越高，库容和库区水面面积As越小，此时，相同下切速率dzs/dt对应的溃决流量越小，故库容与溃决洪峰流量的相关性较坝高更强。

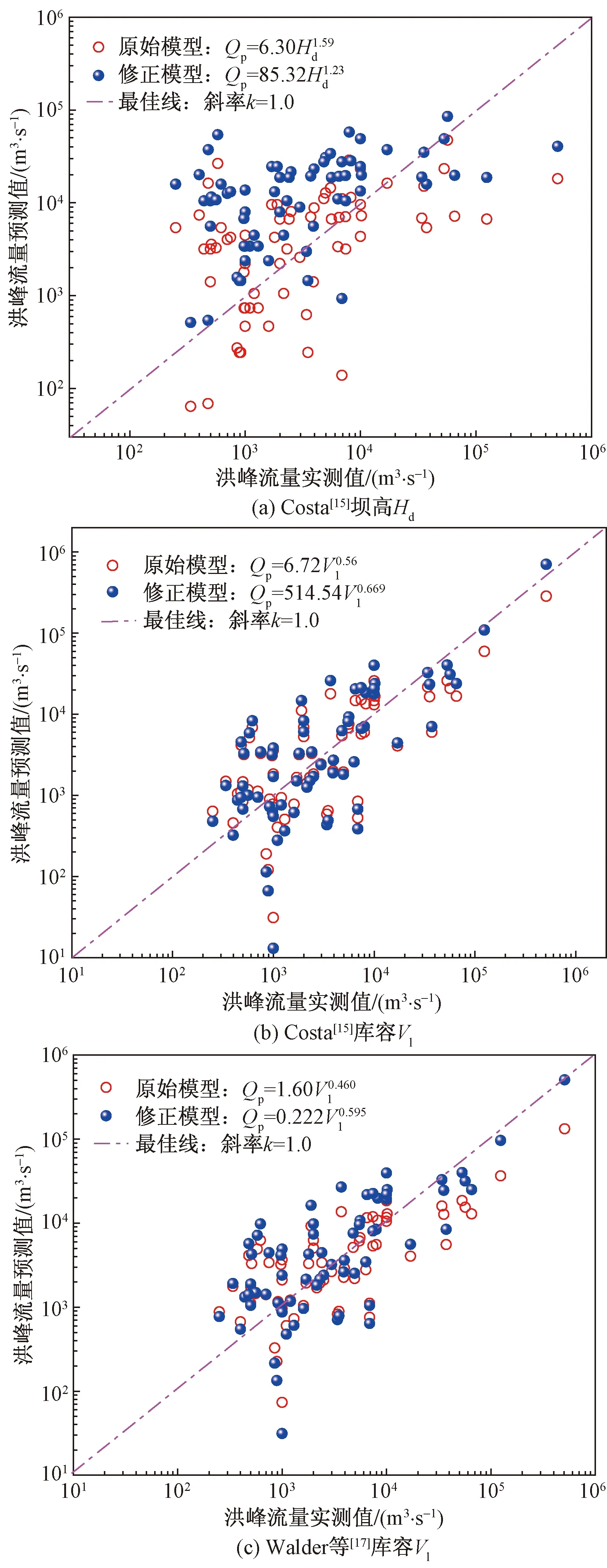
图2 单参数模型Fig.2 Single parameter models

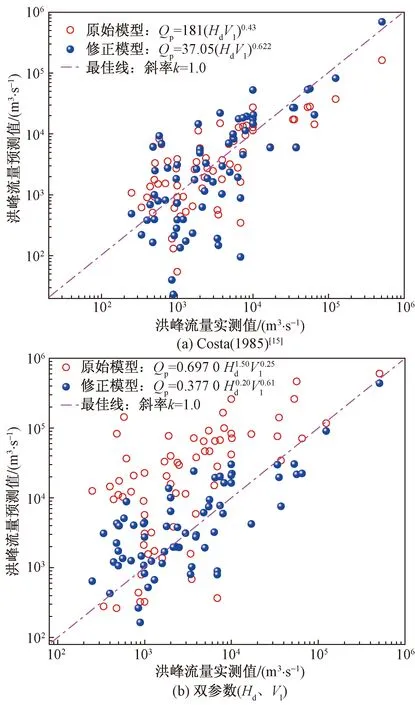
图3 双参数(Hd、Vl)模型Fig.3 Double set parameter (Hd、Vl) model

(4)

式(4)中：t为时间；zs为库水位；As为库区水面面积，通常水位越高As越大；Qin为上游来水流量，一般远小于溃决峰值流量；Qb为溃决流量。

从图3(b)和表5中可以看出，Hakimzadeh等[12]双参数(Hd、Vl)模型在修正前对新样本计算值的R2仅为-0.504 4，修正后达到了0.950 8，RMSE也减小了81.91%，表明若将修正前的计算模型用于新案例的预测，结果的可靠性得不到保证，易出现结果失真现象。同时，Walder等[17]库容Vl单参数模型和Costa[15]双参数(Hd、Vl)模型修正后的R2均有大幅提高，分别从修正前的0.419 0和0.504 5增加至0.972 7和0.847 3，相应的RMSE也分别降低78.34%和44.49%。

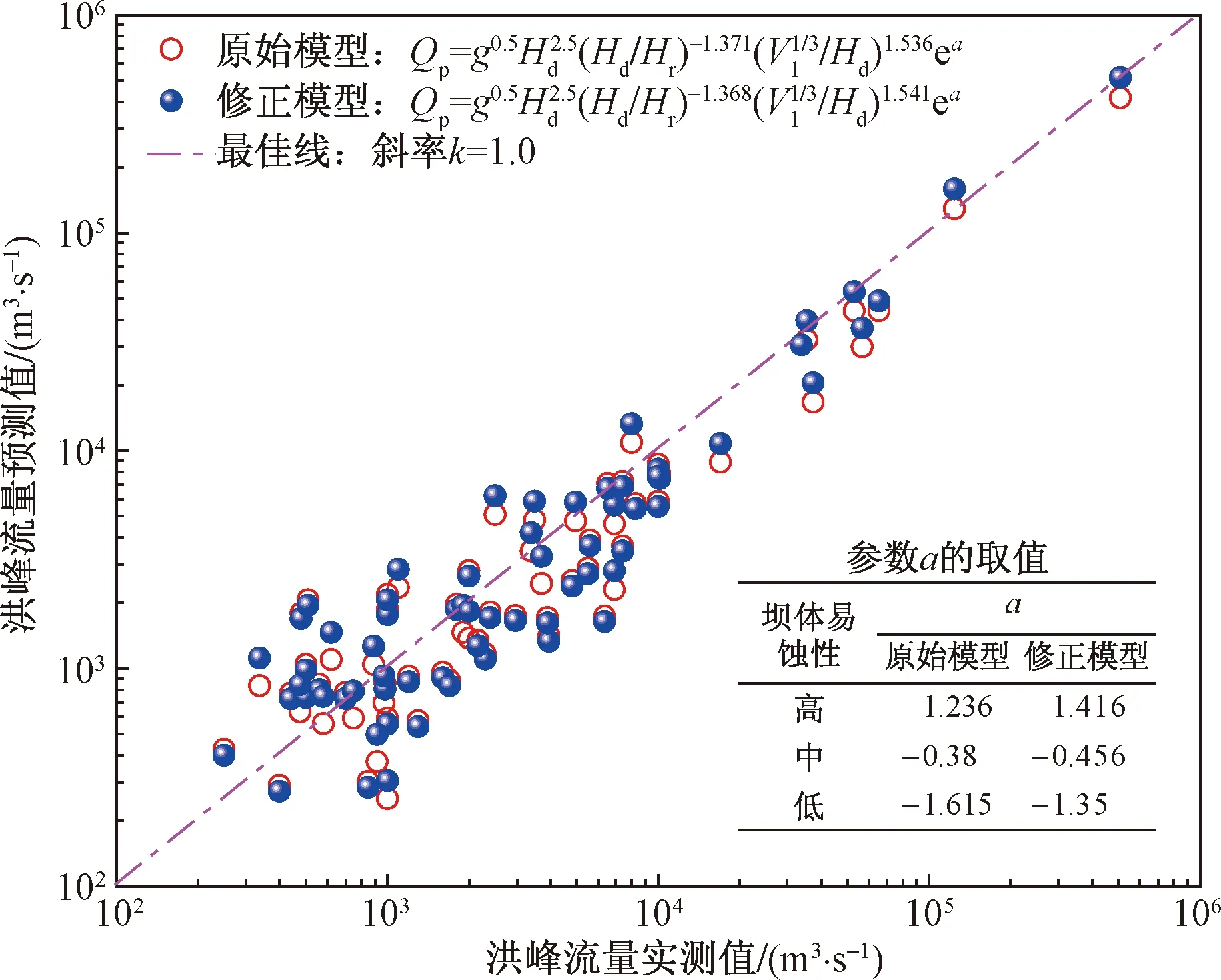
图4 Peng等[10]多参数模型Fig.4 Peng et al’s[10] multi-parameter model

表5 各模型计算效果的度量指标值对比Table 5 Comparison of measure index values for calculation effect of each model

上游水动力条件、坝体形态、坝体内部组成均会对溃决流量产生影响，Peng等[10]多参数模型除了考虑表征坝体上游水动力条件的库容Vl和表征坝体形态的坝高Hd外，还考虑了表征坝体内部组成的易蚀性参数a，将坝体易蚀性分为中、高、低三等。因此，该模型具有更好的稳定性和计算效果，修正后的相关系数有所提高(0.961 7→0.990 9)，但变幅不大，但RMSE减幅较为明显，为51.26%。整体来看，在修正后的所有模型中，Peng等[10]多参数模型的计算效果最好，建议采用该模型进行滑坡坝溃决洪峰流量的计算。

最后，从图2(b)～图4中还可以看出，修正后的模型对流量大于20 000 m3/s的案例计算精度更高，故在计算较大流量时，也可考虑使用图2(b)～图3(b)中对应的模型。

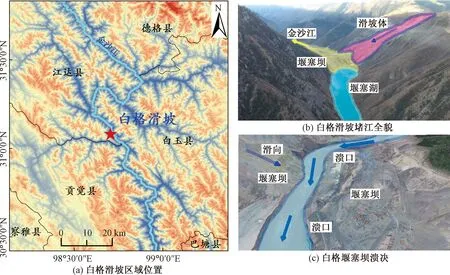
图5 2018年白格滑坡堵江溃决事件Fig.5 Baige landslide dam failure event in 2018

3 案例应用——白格堰塞坝(2018)

3.1 基本概况

2018年10月10日22:06，西藏江达县与四川省白玉县交界处的白格村(98°42′17.98″E，31°4′56.41″N)发生了一次大型滑坡(图5)，滑坡体积达到25×106m3，其中大部分滑坡体堵断金沙江干流河道后形成坝高61 m、顺河长1 500 m堰塞坝；在上游以1 680 m3/s来流量不断蓄入的情况下，水位不断抬升，于10月12日17:30开始漫顶溢流，经处置后库容达到了249×106m3，10月13日14:30溃决结束，整个堰塞坝寿命仅为2.7 d，溃决洪峰流量达到10 000 m3/s[55]。

在10月10日的滑坡坝处置成功约3周后，于2021年11月3日17:15在同一位置又发生了一次大型滑坡，额外的物源和沿程的挟带物质分别为3×106m3和8×106m3，松散物质再次堵断金沙江，形成坝高96 m、顺河长1 000 m堰塞坝，在上游以800 m3/s来流量不断蓄入的情况下，水位不断抬升，经开挖泄流槽处置后库容达到了496×106m3危险性较第一次明显增加，堰塞坝于11月12日04:45开始溢流溃决，11月14日08:00溃决结束，整个堰塞坝寿命为10.6天，洪峰流量达到33 900 m3/s，两次溃决事件均给上下游造成了严重损失[55]。

3.2 修正模型计算结果

Zhang等[55]实地考察了两次白格滑坡堰塞坝溃决事件，获取了详细的溃坝数据，并判定了滑坡坝的易蚀性(表6)。采用修正后的模型对白格两次滑坡堵江溃决事件的洪峰流量进行计算，结果如表7所示。

从表7中可以看出，Peng等[10]模型的计算精度最高，两次溃决事件的计算相对误差仅为24.06%和6.35%，因此建议优先选择该模型。此外，虽然Costa[15]坝高Hd单参数对第一次溃决事件的计算效果较为乐观，但在预测其他样本时仍存在结果较大失真风险，仍不推荐使用；其他模型在计算第二次溃决事件时的效果仍较为理想，因此，当溃决流量大于20 000 m3/s时，其他模型仍推荐使用，在计算流量较小(小于20 000 m3/s)的第一次案例时，除Peng等[10]模型外，其他模型的计算误差较大，但可将上述模型作为参考。

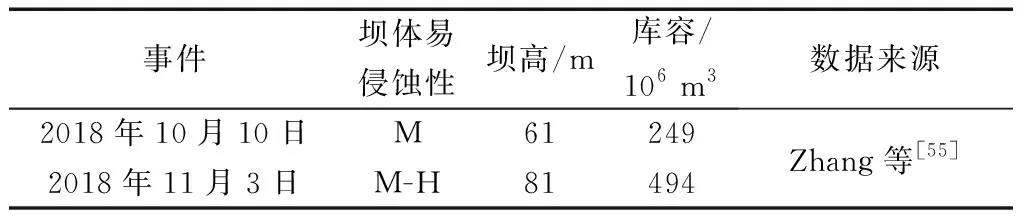
表6 2018年金沙江白格堰塞坝体参数Table 6 The parameters of Baige landslide dam in Jinsha River in 2018

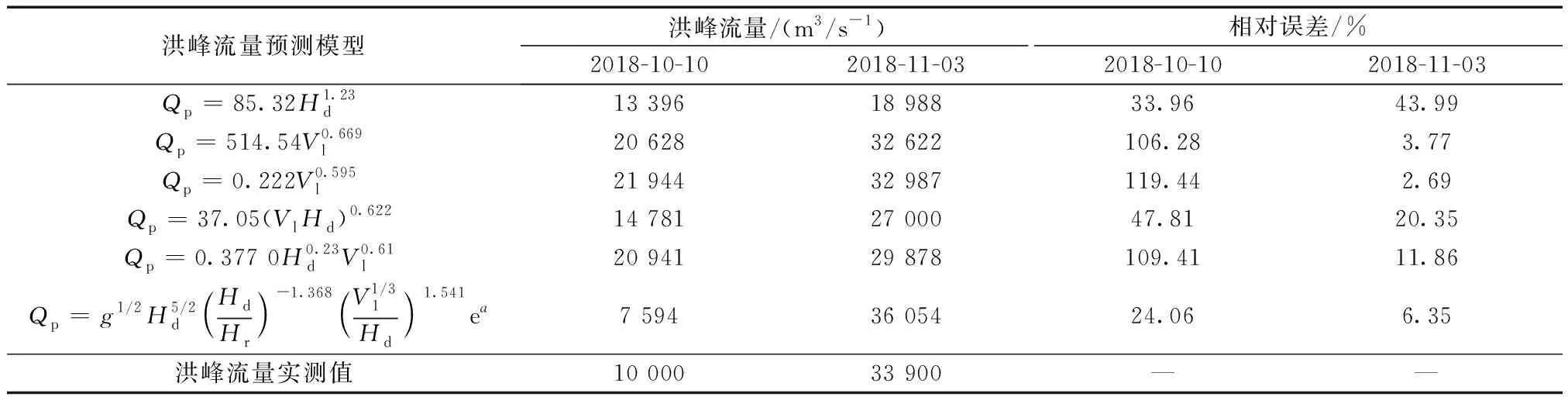
表7 2018年金沙江白格两次堰塞坝溃决峰值流量预测情况Table 7 The predicted results of peak discharge of Baige two dam failure in Jinsha River in 2018

4 结论

通过文献查阅，获取了来自全球具有详细资料记载的67个滑坡坝溃决案例，并采用该数据库对已有的滑坡坝溃决洪峰流量经验模型进行修正，最后采用修正后的模型对白格堰塞坝两次溃决事件进行计算对比，得出如下主要结论。

(1)本文数据库中的案例从原来最多的45例扩充至67例，最大峰值流量是原有数据库中的4.1倍，数据库包含了非常极端的情况，修正的模型适用范围更广。

(2)修正后模型的计算效果较修正前均有提升，且大部分模型的RMSE和R2均有明显改善，R2最高能达到0.990 9，但Costa[15]坝高Hd单参数修正后的R2仍非常低(仅为0.074 6)，表明该模型中坝高Hd与溃决洪峰流量的相关性不明显。

(3)在所有模型中，Peng等[10]模型的计算效果最好，应用时建议优先选用该模型。当溃决流量较大(大于20 000 m3/s)时，其他模型仍具有较高的计算效果，反之，计算效果较差，可作为参考使用，该结论与采用修正模型对金沙江白格两次滑坡堵江溃决事件进行计算对比后的结论一致。

最后，所涉及的模型均为经验参数模型，公式的回归系数对样本容量(滑坡坝案例总数)较为敏感，今后需不断扩充新样本对公式进一步修正。同时，针对滑坡坝溃决的复杂水土耦合问题，需从本质出发，阐明其溃决机理，最后构建多影响因子的滑坡坝溃决洪峰流量预测模型。