保守系统中非线性耦合振子间的能量传递*

王锦涛 谢勇

（西安交通大学机械结构强度与振动国家重点实验室，陕西省无损检测与结构完整性评价工程技术研究中心，西安 710049）

引言

靶能量传递（Targeted energy transfer，TET）是Kopidakis等[1]发现的一种能量由主振子向NES传递的现象，能量传递的过程非常短暂且不可逆，每次传递的能量比较精确.非线性能量阱（Nonlinear energy sink，NES）[2]可以实现靶能量传递使振动能量单向传递至NES并被其耗散掉.

非线性能量阱的动力学特性非常复杂，甚至对于两自由度非线性能量阱（2-DOF NES）现在还难以得到完全精确的解析分析，由于NES可实现高效减振，因此对NES进行理论研究仍然具有重要价值.国内外学者对NES的复杂非线性动力学进行了大量研究.Gendelman等[2]最早对非线性能量阱的靶能量传递进行了研究.文献[3]研究了线性振子耦合小质量非线性振子的力学特性，发现了两种可引发靶能量传递的条件，一种是1：1振动俘获，另一种是非谐振条件下非线性振子的高频振动.文献[4]中在系统无阻尼情况下用非平稳变换的方法得到了周期解，然后通过频率－能量图揭示了该系统的分岔结构，基于复变量－平均法对引发靶能量传递的分谐振，1：1内共振及非线性拍（nonlinear beat）现象作了分析.文献[5]详细分析了三种引发靶能量传递的情况.文献[6]研究了系统输入不同大小脉冲激励下的周期轨道和准周期轨道.文献[7]用简化的动力学方程说明当初始条件在一定范围时NES的效率较高.该研究可作为对文献[8]中不变流形研究的补充.文献[9]通过优化NES的参数实现了最优靶能量传递，并对NES的吸振效率进行了试验验证.文献[10]研究了一个二自由度非线性振动系统，给出了其频能图以及内共振情形的局部化非线性模态流形.提出了势能曲面上模态迹线的概念，发现系统产生内共振的标志之一是两条模态迹线存在交点.发现能量传递现象与两种机制有关：非线性模态局部化以及局部化模态之间的内共振；参与内共振的各个模态在迹线交叉点处实现了能量交换.另外，对NES的研究也做了一些实验验证[11-13]，证实了很多理论研究的成果.

靶能量传递主要通过共振俘获实现[4]，是NES抑制结构自由振动的主要原理.在研究NES抑制结构自由振动时，Sapsis等[14]把NES中取得最大能量耗散比的情况定义为最优靶能量传递，并证明了当实现最优靶能量传递时，主振子的振动能量会在半个慢变周期（super-slow half cycle）内达到零，这便是目前最直观判断是否为最优靶能量传递的方法.虽然单自由度NES通过最优靶能量传递可以达到很高的振动抑制效率，但要使靶能量在非线性耦合振子间能够完全传递需要两个条件：第一、主振子的初始振动能量必须等于某一定值.若主振子的初始振动能量过小，则靶能量的传递就无法实现，这时NES对系统的振动抑制几乎不起作用，如果初始能量过大，会在一定程度上降低NES的振动抑制效果[14，15]；第二、实现最优靶能量传递需要 NES 具有一定的质量、以上两点仅为实现最优靶能量传递的定性结论，无法根据NES质量和主振子的初始振动能量设计NES.目前虽然有方法计算出了实现最优靶能量传递的NES的最小质量以及所需的初始能量大小，但是对能量传递过程中一些问题的揭示还不够完整[16-18].

本研究对实现最优靶能量传递的NES质量和初始能量条件进行了定量分析.通过建立1：1内共振条件下系统的慢变方程，对保守系统中振动能量可以完全由线性振子传递至NES所需的最小质量和初始能量进行了理论推导和数值验证.根据研究结果可以设计NES的质量和初始能量，使NES实现最优靶能量传递.对原系统的数值仿真表明NES的质量会影响能量传递的暂态和能量交换时间，另外，靶能量的传递与初始能量的形式也有关.

1 非线性耦合振子系统的力学模型

1.1 原系统模型

在图1中，非线性耦合振子系统由一个线性主振子和立方刚度NES构成，系统方程如下：

图1 非线性耦合振子系统模型Fig.1 Nonlinear coupled oscillator system model

1.2 慢变力学模型

2 保守系统中能量在两振子间的完全传递

2.1 慢变系统的两个首次积分

2.2 推导能量完全传递时的NES质量条件

2.3 推导能量完全传递时的初始能量条件

3 数值验证和分析讨论

3.1 慢变系统能量完全传递条件的验证和分析

由于在推导能量完全传递条件的过程中进行了多次变量替换，导致参数的量纲失去了明确的物理意义，所以数值仿真的参数没有标明单位.选取参数分析哈密顿系统（21）的θ-δ相轨迹.对NES和主振子的质量比选取ε>ε21、ε=ε21、ε<ε21三种情况（其中两振子的临界质量比ε21=0.0557）来验证前面推导的临界质量比是否正确.每种情况中不同的刚度比值k21分别对应弱非线性和强非线性系统.图2-图3和图4中每条相轨迹表示不同的n值，黑色虚线代表n=n0的相轨迹.

图2 θ—δ相平面图，ε=0.1Fig.2 Phase-plane portrait，ε =0.1

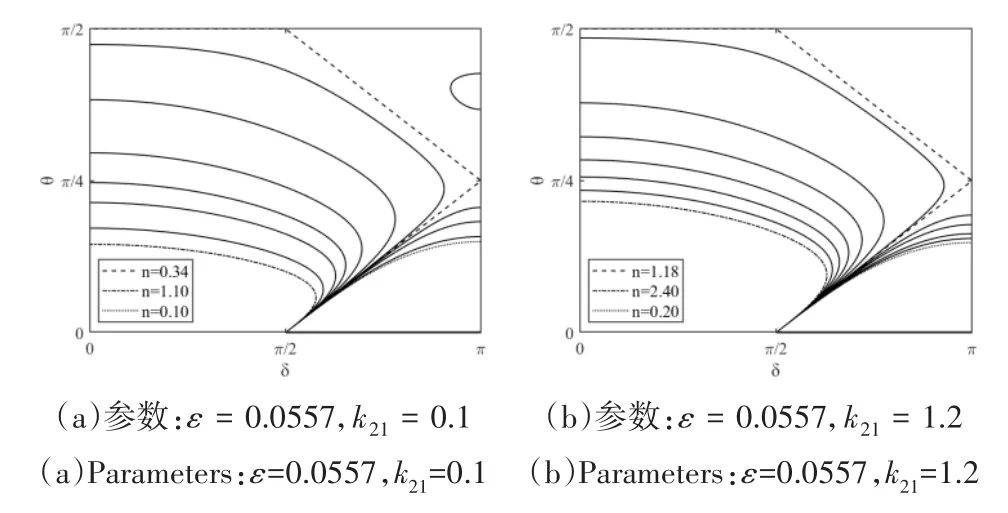
图3 θ—δ相平面图，ε=0.0557Fig.3 Phase-plane portrait，ε =0.0557

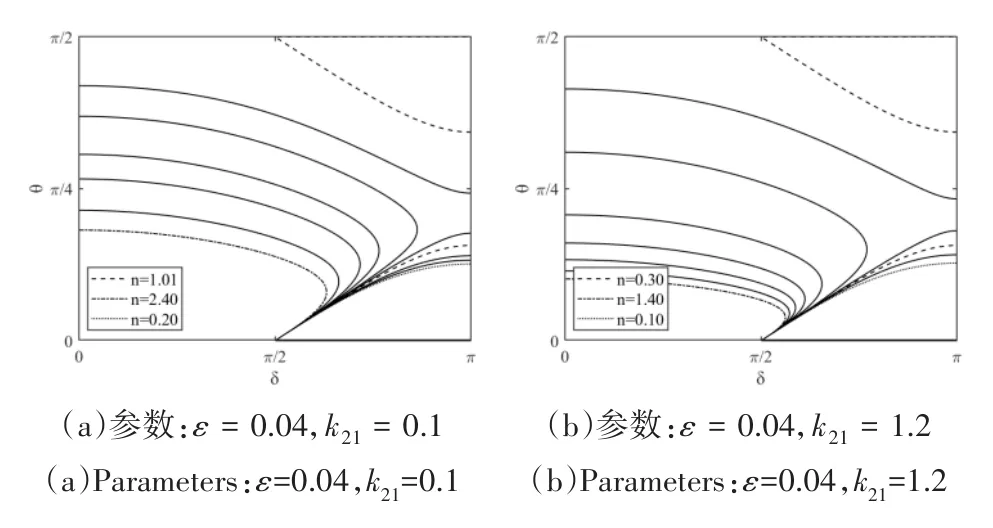
图4 θ—δ相平面图，ε=0.04Fig.4 Phase-plane portrait，ε =0.04

在图2中非线性振子NES与线性主振子的质量比ε>0.0557.从图2可以看出，尽管k21取值不同，但只要n=n0，θ的值都可以从0连续变化到π/2.由（17）式、（18）式和（19）式及前面的分析可知，该过程就是线性主振子能量完全传递至NES的过程.当n≠n0时，θ的最大值均没有达到π/2，从（17）式可以看出，此时线性主振子的振动能量最小值E1min>0.由式（18）可知，此时只有部分振动能量从线性主振子传递到了非线性振子NES，传递率没有达到100%，且n值偏离n0越大，传递到NES的能量就越少，能量传递效率也越低.图2的仿真结果验证了前面的分析结论：要使哈密顿系统（21）中θ能够由0连续变化到π/2，必须满足n=n0这个条件，且当θ=π/2时，δ=π/2，这也正和前面的研究结果（32）式相吻合.

在图3中，NES与主振子的质量比ε=0.0557.从图3可以看出，系统刚度不论强弱，只要n=n0，θ都可以从0连续变化到π/2.和图2不同的是，变化过程中δ恰好达到了边界值π.当n取其它值时，θ的最大值均小于π/2，能量都没有完全传递至NES.

从图4可以看出，如果继续减小非线性振子NES的质量，当n=n0时，θ的最大值只有0.48左右.δ在能量传递过程中虽然可以达到最大值π，但是δ的变化已经超出了（0≤δ≤π）的范围，相轨迹在δ=π处被切断，θ只能在0和最大值之间循环，系统无法实现完全能量传递.图5中每条曲线代表在n=n0下，在NES质量不同时系统的能量传递过程，其中黑色虚线表示n=n0，ε=0.0557时系统的能量传递过程.

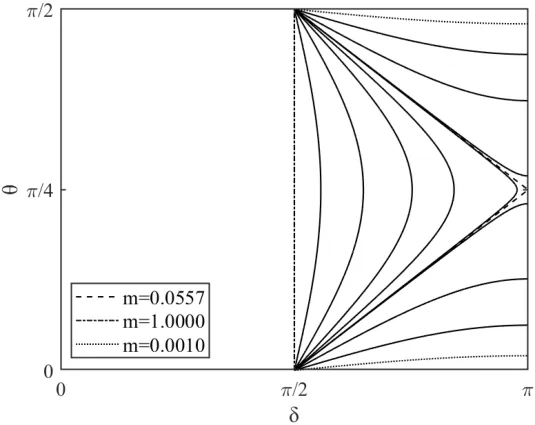
图5 θ-δ相平面图，n=n0Fig.5 Phase-plane portrait，n=n0

图2-图4验证了只要n≠n0，主振子能量就不可能完全传递至NES.图5中黑色虚线的左边区域表示都能够实现能量完全传递，从图5中可以看出，系统要实现能量完全传递还须满足NES的质量比大于某一值，而且证明了该值确实为0.0557，从而验证了临界质量比的正确性的.综合图2-图5可以得出如下结论：只有在n=n0，ε≥0.0557的情况下，系统才能实现能量完全传递.至此，完成了对慢变系统中能量完全传递条件的验证.

3.2 能量完全传递条件在原系统中的验证和分析

观察由（41）式、（42）式和（43）式计算得到的初始条件能否使振动能量在保守系统（5）中的两振子间完全传递.两振子的能量分别按以下两式计算：

E1、E2分别为线性主振子和NES振子的能量.初始条件按（41）式选取：

从图6和图7可以看出，NES与主振子的质量之比ε≥0.0557，此时无论系统的非线性刚度强弱，主振子能量都降到了零，也就是说振动能量在两振子之间都实现了完全传递，这与图2-图3以及前面的结论正好吻合.

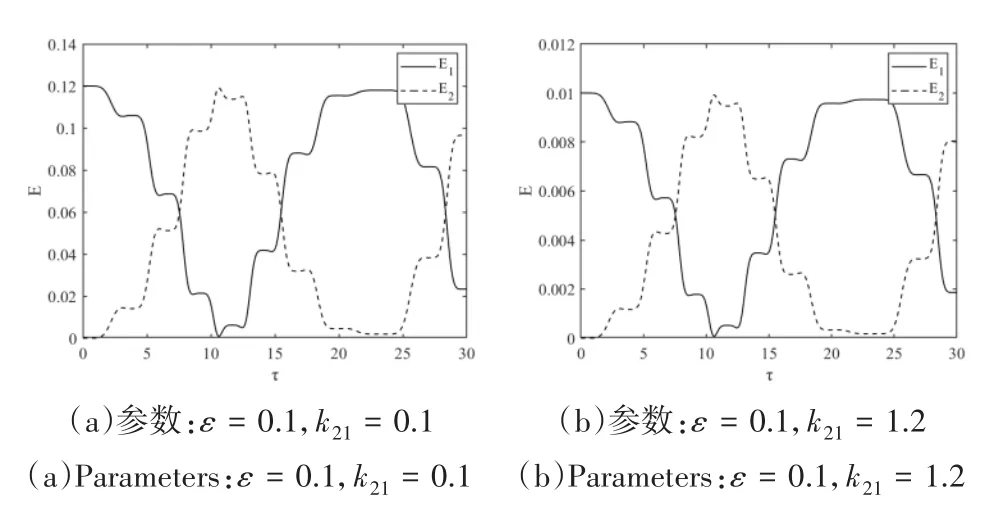
图6 两振子间的能量传递Fig.6 Energy transfer between two oscillators

图7 两振子间的能量传递Fig.7 Energy transfer between two oscillators

从图6-图9可以看出NES的质量越大，系统能量交换的周期越短，而刚度对能量交换的周期基本没有影响，但是对暂态和振子能量的变化率有影响.图8是在n=n0，ε<0.0557下系统的能量传递过程，经过观察分析图6-图9，可以得出下面结论：第一、系统两振子进入能量传递前的暂态时间与振子的质量有关；第二、系统经过暂态后，两振子能量交换的时间与振子的质量有关.从图6-图7可以看出系统实现了完全能量传递，这与图2和图3一致.图9中系统在n=n0，ε=0.04情况下基本实现了完全能量传递，然而在图4中能量传递效率最高却只有0.48左右，说明由近似慢变系统推导出的临界质量比确实有偏差.

图8 两振子间的能量传递Fig.8 Energy transfer between two oscillators

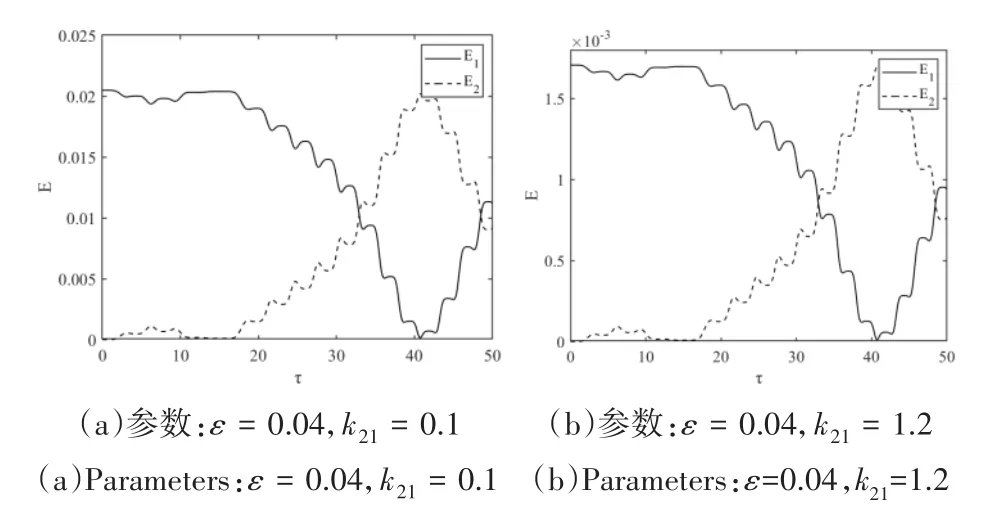
图9 两振子间的能量传递Fig.9 Energy transfer between two oscillators

图10的初始位移按图9的1.25倍选取，对比图9和图10可以看出：第一、图9实现了完全能量传递而图10没有；第二、图9引发能量传递的暂态时间比图10长得多，能量交换时间也比图10长，这验证了系统要实现能量完全传递初始能量必须等于某一定值，说明初始条件会影响能量传递.从图10可以看出此时能量传递率比较高，事实上这和前面得出的结论并不矛盾，从图4可以看出，虽然在n=n0处θ的最大值很小，能量的传递效率不高，但n>n0时，虚线左边的曲线仍然可以达到较大的θ值，即NES可以实现较高的能量传递效率，当n=1.1245时，系统的能量传递率高达96%，按照前面对慢变模型的分析，这时的能量传递效率确实没有达到百分之百，图4和图10也互相印证了这一点.

图10 两振子间的能量传递，xten10=1.25xnine10Fig.10 Energy transfer between two oscillators，xten10=1.25xnine10

初始条件按（42）式选取：图11按照（42）式选取初始速度，图6和图7按照（41）式选取初始位移，系统初始能量相同，其它参数一致，得到的结果却不同；图6和图7系统实现了完全传递，图11（a）系统的振动能量虽然在两振子间高效传递，但没有达到完全传递，另外它的能量交换持续时间比图6更长.图11（b）在质量比取0.0557时，振动能量便无法向NES传递了，这说明非线性能量阱的能量传递与初始能量的形式有关，而且预测的临界质量比也有偏差，这种偏差是由平均法、多尺度法以及龙格库塔法造成的.按照（42）式可以预测实现完全能量传递时所需的初始速度，如图12，在质量比ε<0.0557时，系统已无法实现靶能量的完全传递.

图11 两振子间的能量传递Fig.11 Energy transfer between two oscillators

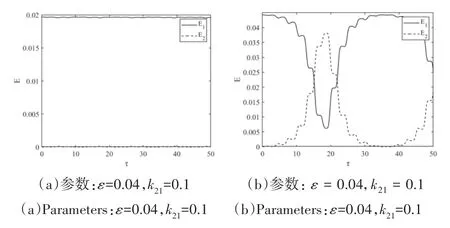
图12 两振子间的能量传递，b10=1.5a10Fig.12 Energy transfer between two oscillators，b10=1.5a10

在图12中质量比ε取0.04，初始速度按式（42）的1.5倍选取，可见能量的传递效率较高.这表明即使NES的质量小于临界值，若提高线性振子的初始能量，也可以取得较好的能量传递效果.需要说明，这种现象与前面的推导并不矛盾，从图4可以看出，虽然在n=n0处能量的传递效率不高（θ的最大值很小），但在n>n0时，虚线左边的曲线仍然可以达到较大的θ值，即NES可以实现较高的能量传递效率，按照前面对慢变模型的分析，这时的能量传递效率无法达到百分之百.另外从图7和图9、图11和图12可以看出在相同条件下，势能形式的能量比动能更容易实现系统的能量传递.

初始条件按（43）式选取：图13的初始条件按（43）式计算，虽然系统能量都实现了高效传递，但都无法实现完全传递.图6和图7实现了完全能量传递，图13（a）虽然质量比满足条件，但初始能量并没有满足，说明系统的完全能量传递和系统的初始条件有关，也验证了系统的初始条件必须为（41）式或（42）式才能实现完全能量传递.图13（b）中NES与主振子的质量比ε<0.0557，可以看出振动能量在两振子之间实现了高效传递，但没有达到完全传递，这是因为质量比和初始条件都没有满足完全能量传递的条件，图4和图13（b）互相印证了这一点.

图13 两振子间的能量传递Fig.13 Energy transfer between two oscillators

暂态transient：系统开始振动至两振子开始发生能量换的时间.能量交换时间exchange：主振子能量传递给NES达到最大，然后NES又返还给主振子的能量达到最大时的时间.

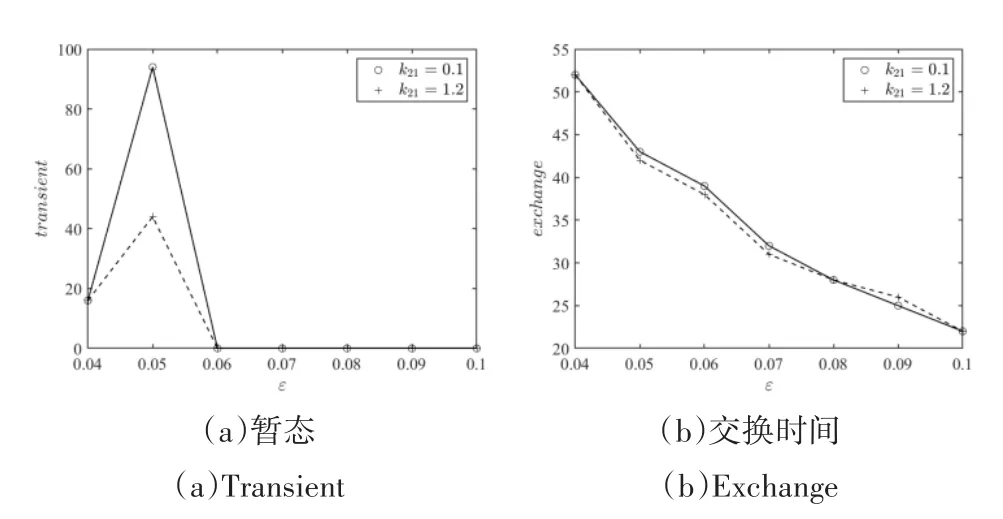
图14 暂态及能量交换时间Fig.14 Transient and exchange time

能量传递率η：主振子传递给NES的最大能量与系统初始能量的比例.

图15 不同参数条件下的能量传递率Fig.15 Energy transfer efficiency with different parameters

4 结论

（1）两自由度非线性耦合振子的保守系统中，实现主振子与非线性振子NES之间的能量完全传递必须满足两个条件：第一、NES具有一定的质量，且主振子和NES振子的质量比必须大于等于0.0557；第二，主振子的初始振动能量必须等于某一定值，而且该值可按（41）式和（42）式给出.

（2）系统两振子进入能量传递前的暂态时间与振子的质量有关.NES质量越小，两振子能量交换的时间越长，当质量比大于等于0.0557时，两振子可不经过暂态而直接进行能量交换，当NES质量过小时，适当提高非线性耦合振子的初始能量可实现能量高效传递.

（3）非线性耦合振子系统的刚度会影响能量传递的暂态时间，但对能量交换的时间影响不大.

（4）非线性耦合振子初始能量的形式会影响系统的能量传递，在系统参数相同，初始能量一样多的情况下，势能比动能更容易引发系统能量传递.