基于模糊关联算法在财务指标分析系统中的应用①

张卫东

(广东工商职业技术大学 财经政法学院,广东 肇庆 526040)

0 引 言

财务分析是一个企业领导者明确其企业财务状况和经营状态的关键环节[1]。近些年,在对财务指标系统的研究中,怎样从大量财务指标中提取有价值的信息,并深入分析,从而构建完善的财务指标分析系统成为了经济领域中一个亟待解决的问题[2]。将模糊算法融入到财务指标分析过程中,在SAPBW环境下,针对企业实际财务分析决策的需求,给出财务指标分析的框架,并在此基础上,提取海量财务指标中有效信息。实验仿真证明,基于模糊关联算法的财务指标分析系统指标分析精度高,能够为企业领导者的决策提供科学依据[3]。

1 财务指标分析系统需求分析及其框架设计

1.1 财务指标分析系统需求分析

对企业财务指标(包括经营、偿债、盈利、发展等方面)分析可以实时掌握企业财务管理状态,杜绝企业决策的严重失误及不稳定性,通过迅速发出预警的机制组建防御制度,由此提升企业抗财务风险的能力,促使企业财务管理保持平稳状态[4]。

1.2 财务指标分析系统的框架设计

一个完整的财务指标系统可以分为数据(处理,存储,访问,获取)4个层面。其设计框架如下:

系统最末层是数据获取层,大部分是各类凭证数据。将这部分数据存入到数据仓库中要先对原始数据进行数据清理、抽取、转换,归类。因此先依据SAP BW的数据抽取制度将SAP R/3源系统数据源内的全部数据依据制定的计划有序上载,在上载到PSA时在根据信息源对照和更新制度的清洗转换上载至信息配备者ODS中,在此基础上再变换进入信息立方体[5]。

数据存储层的作用是存放经过一系列处理后的财务指标分析系统数据仓库中的全部数据。数据访问层主要是客户和系统相互融合的切入层,企业决策者将依据这层表现出的报表、图像、数据搜索到自身想要得到的详细数据,并可以在数据分析结果中获取有价值的信息对更深入决策配备依据。财务指标分析系统的功能模块如下图。

功能模块主要分为(数据准备、指标分析、报表输出)模块。其中数据准备模块的作用是对R/3中的数据进行统一格式化处理,并将处理后的数据存储SAP BW内。指标分析模块是对经营、偿债、盈利、发展四个维度财务指标分析的过程。报表输出模块是将分析结果详细的呈现给用户的过程。

2 财务指标分析系统优化设计

2.1 财务指标特征的提取

对财务指标分析中,将模糊二阶段分类算法引入到财务指标分类中,在指标训练集和数据集中提取系统的输入变量的特征集,进而对数据样本进行划分。具体步骤如下:

假设训练集的输入和输出已确定,p代表训练集,（x1,i,x2,i,…,x n,p,y p）代表训练集中n个输入和输出对。利用公式(1)表示n个输入和输出对的语言变量升序排列。

如果R T代表组建数量为N A的样本数据输出和输入间的相似关系,则利用公式(2)和(3)计算其N A维相似矩阵。

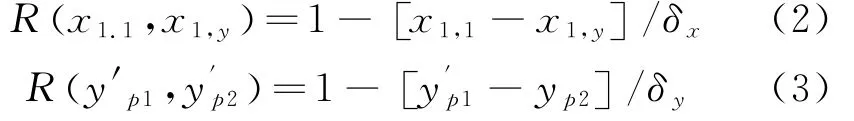
δ为常数,需要和式(4),(5)条件相匹配。

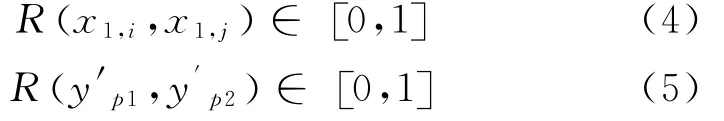
则利用公式(6),(7)计算（δx,δy）。

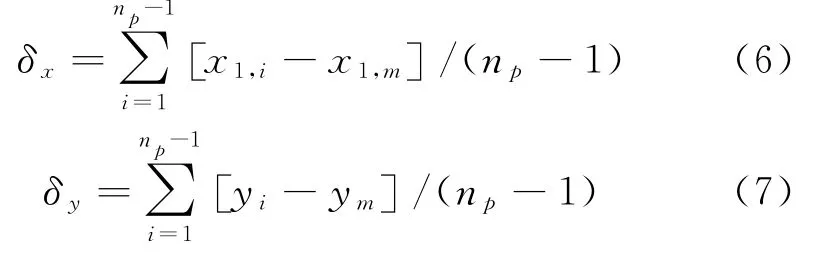
式(6),(7)中x1,m代表整体指标样本数据中系统首个输入变量的最大值,x-1则代表首个输入变量,y m则代表输入语言变量的最大值。在构建数量为N样本数据间的相似关系的基础上,获取R s代表的N维相似矩阵,将该矩阵变化为一个等价矩阵,利用式(8):

如果R e,a代表等价矩阵R e的α截矩阵,则依据R e,a进行样本数据分类,在满足条件R e,a（x1,i,x1,j）=1的基础上,将x1,i和x1,j所代表的指标数据分为同一类。如果α有所变化,R e代表的等价矩阵判断的分类所包含的元素逐步增多,并持续归并在同类中,所以α决定了样本数据类别数量。

假设Gj（j=1,2,…r）代表指标分析训练集的输入和输出对划分的r个子集,则利用式(9)计算。

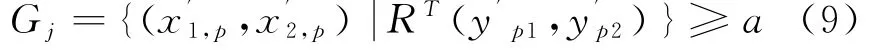
其中α代表指标数据分析划分训练集的阈值,r代表最终取的分类数量。可知分类的数量影响了隶属函数的数量;如果将指标分析样本分为训练和检验集,则N A代表训练样本集,在N A上计算财务指标的模糊特征子集。依据模糊划分计算各个子集输出和输入变量的隶属度函数,利用式(10)-(12)计算。

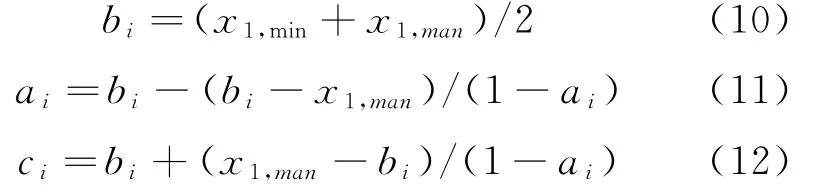
式(10)-(12)中x1,min,x1,max分别代表第i个子类别中的首个输入变量的最低值和最高值。

2.2 模糊关联算法的优化应用

模糊识别算法的原理是根据财务指标分类后样本集的优劣程度划分等级。在指标分析中将财务指标分为C个等级,并且利用各类样本等级隶属度组成模糊识别矩阵,由U表示。如果训练集中样本数量为m个,则利用C和m可以组建s代表模糊聚类中心矩阵,则测试样本可依据s代表的模糊聚类中心矩阵反向推导U'表示的财务指标模糊识别矩阵,进而分析测试样本优劣程度。

由于不同指标存在数量级差异需要归一化处理,用R代表指标训练集的隶属度矩阵。企业财务指标价值不同,所以各财务指标会有不同权重,各指标权重由式(13)表述:

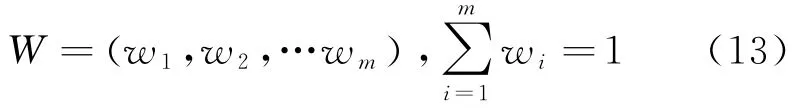
在公式(13)中m代表指标数量。假设j代表训练样本,h代表样本类别,则利用下式计算j和h特征值聚类中心间的不同。

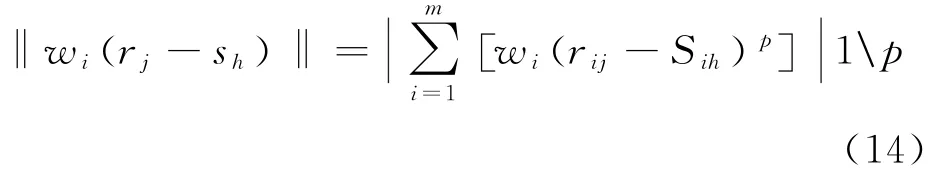
式(14)中距离参数由p表述。则利用下公式计算p的加权广义欧氏权距离。

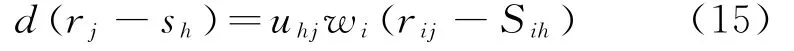
要想实现指标训练样本集针对整体类别加权广义欧氏权距离平方和最低,则需要利用下组建目标函数。

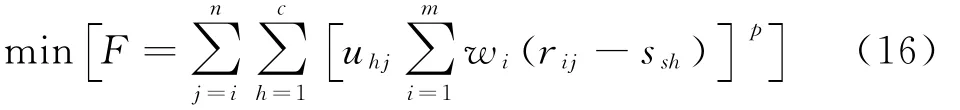
假设满足p=2的条件,则财务指标分类目标函数可以表述为式(17):

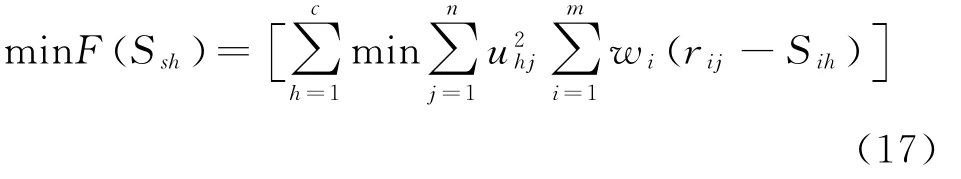
综上步骤,可以获取S代表的模糊聚类中心矩阵。利用式(18)组建格拉朗日函数:

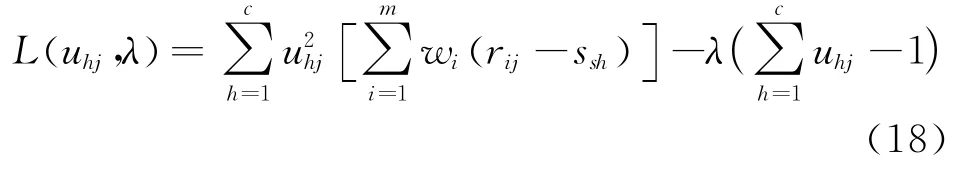
由此获取U'代表的模糊识别矩阵。如果有一个（x ij）m×n代表企业样本集,其中企业数量为n,财务指标数量为m,那么将x ij定义为样本j的指标特征值,利用下述步骤组建指标的模糊识别矩阵:

(1)训练样本的模糊识别矩阵。利用专家对财务指标训练样本内的各类财务指标优劣度划分为c个等级,获取U=（u hj）代表的等级评估样本够成的模糊识别矩阵,其中（u hj）代表企业财务指标样本j归类为h的相对隶属度。如果样本j属于h类,则其隶属度的值为1,相反,如果不属于h类,则其隶属度得值就会是0,利用下式进行表述:

(2)基于测试样本的最优模糊识别矩阵。利用R'代表的隶属度矩阵和S代表的财务指标训练样本的最优模糊聚类中心矩阵可计算U'代表的财务指标测试样本最优模糊识别矩阵,进而作为财务决策的最终指标(详见图1)。

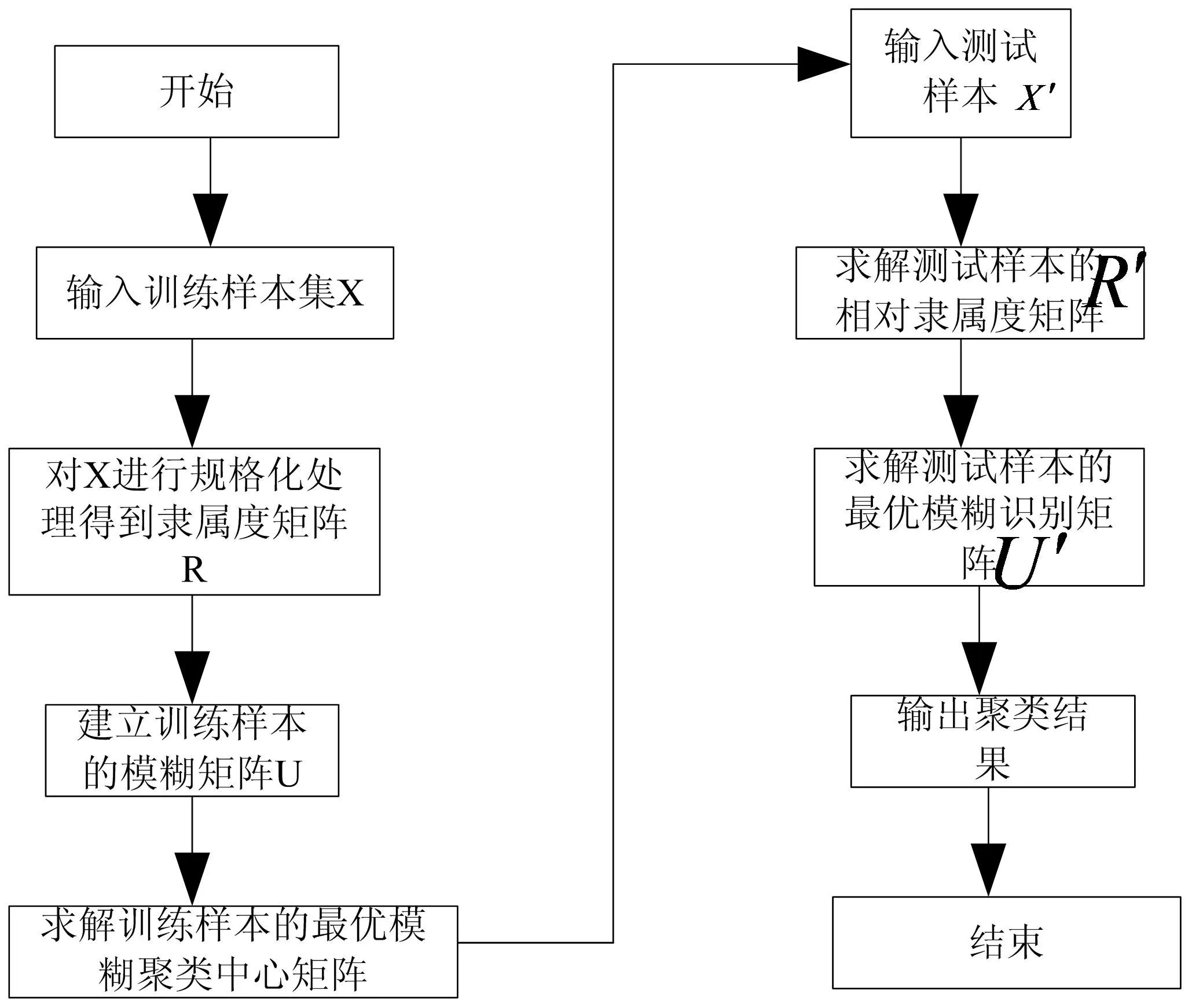
图1 模糊识别算法流程

3 实验仿真分析

为了更好展示模糊关联算法在财务指标分析中的作用,实施仿真实验。所用仿真数据集是德国某企业信贷信息的财务指标统计数据集,在该数据集中含有指标信息1000条记录,将其百分之六十作为训练数据集,百分之四十作为测试数据集。

3.1 评价指标的设定

将实验设定为两个阶段,第一阶段将财务指标分类误差作为主观评价指标,观察模糊关联算法在财务分析系统中的表现。第二个阶段,将文献2算法作为对比算法,将拟合优度作为客观评价指标,定义两种不同算法在财务指标分析中的综合有效性。

3.2 实验结果分析

(1)指标分类误差

基于模糊关联算法进行财务指标分析,以分类误差作为判断准则,结果见图2。

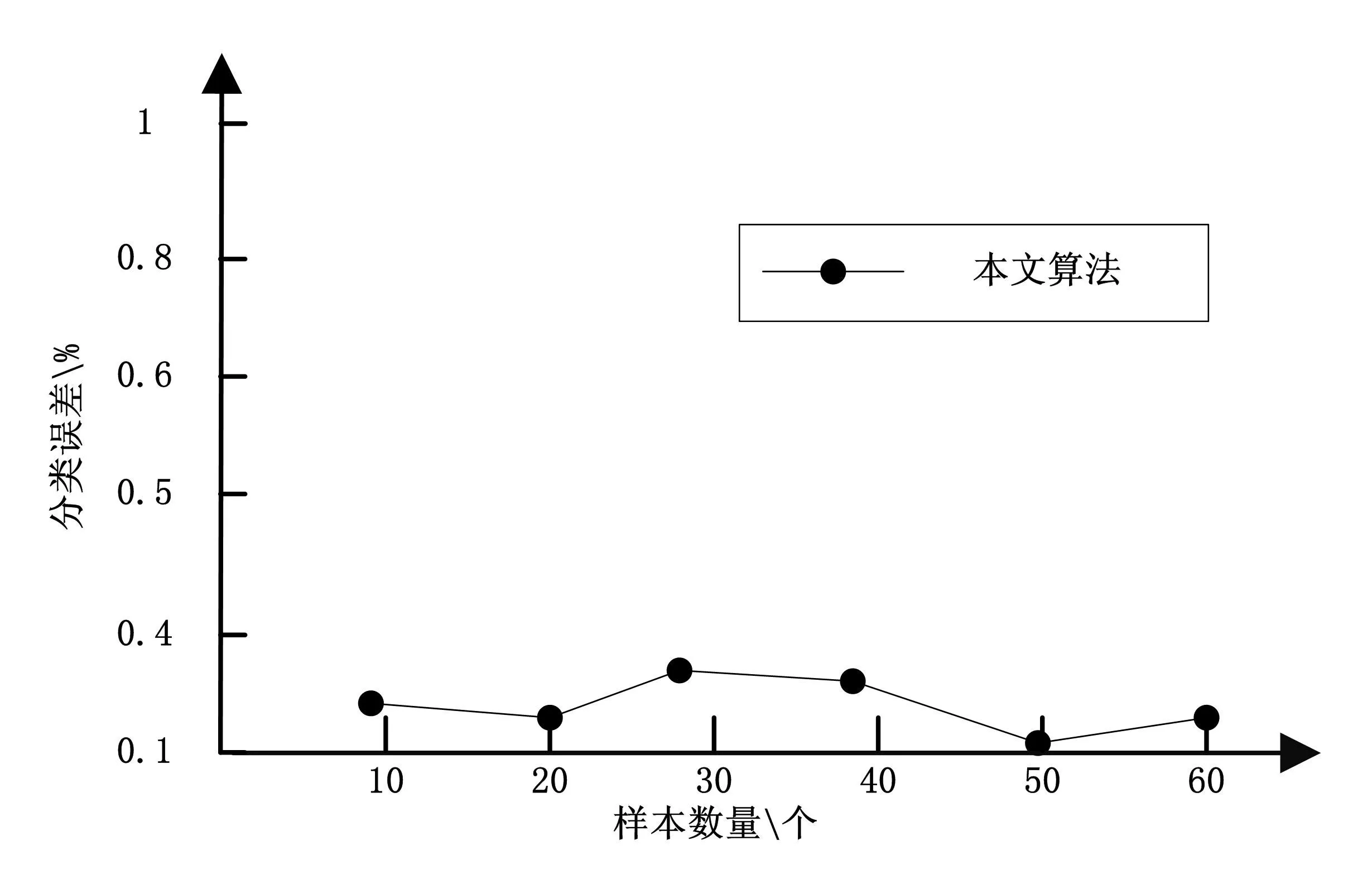
图2 本文算法的指标特征分类误差

由图2看到模糊关联算法进行特征分类的误差在较低范围内。可见本文将二阶段分类算法引入到财务指标分析中,充分降低了指标特征提取误差,并计算每个特征的隶属度函数,提升了分类的精确度。

(2)指标分析的拟合优度对比

由图3看出提出的模糊关联算法能有效分析出企业财务经营状态,并和实际的财务状态相吻合,这是因为在利用本文算法进行财务指标分析时,针对不同财务指标类型计算出权重向量,并组建其财务指标类型的目标函数,对其指标类型进行寻优,在此基础上组建了财务指标识别最优矩阵,进而满足了财务指标分析对分析精度的需求。

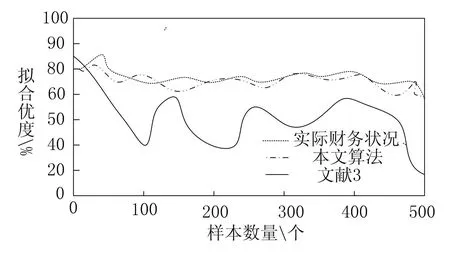
图3 不同算法的指标分析拟合优度对比

4 结 语

将所提模糊关联算法引入到财务指标分析系统中,建立指标分析系统,通过对比专业人士对几家企业的分析结果,发现系统分析结果接近于企业实际财务状况,进而证明了系统可以促使企业管理者更好,更全面的熟悉企业的财务运转状态,并且无需掌握专业的财务分析流程,为企业决策者及时监督其自身经营状态提供了可行的依据。