利益攸关方视角下的装配式产业链利益分配①

胡龙伟, 夏思雨, 王金荣

(青岛理工大学管理与工程学院,山东 青岛 266520)

0 引 言

装配式建筑与传统的现浇混凝土建造方式相比,装配式建筑具有生产更高效、资源更节约等特点,且对于推动建筑产业健康发展有重大意义[1]。推动装配式建筑的健康发展,需要行业形成一个完整的市场和供应链,足够让众多中小企业发展起来,从而促进产业链企业的资源整合。一个完整的供应链,需要各独立经营的企业为了获得更高的利润通过供应关系联系起来,而科学、合理的利益分配机制是各企业合作的基础,是保证产业链成功运行和健康发展的关键问题[2],建立一套普适性的装配式产业链利益分配模型是市场迫切需要的。对收益分配多采用博弈论方法。段文吉等通过合作博弈对装配式建筑产业链进行利益分配,证明了合作博弈对于装配式产业链的适用性,同时提出可以通过因素引入加以修正会更加全面、公正[3]。王文静等人在传统的Shapley值法的基础上将风险分担等引入对其进行修正,并通过与传统分配方式的对比证明其科学性及合理性[4]。但在现有的研究仅仅只是将因素简单的引入分配模型,认为不同的因素对于整个产业链的影响是相同的,这点显然是不符合实际的,在此基础上通过改进的灰色关联法将引进的因素赋予权重,并通过TOPSIS将已有的数据进行处理计算出加权改进系数。

1 装配式建筑产业链分析

1.1 装配式建筑产业链参与方

对装配式混凝土建筑的进行了深入的分析,根据不同的工作运营的主体间相互作用及产品构件的不同流向,构建了关于装配式建筑产业链的模型[5],整个装配式建筑产业链的有机协调运作及相互之间的关系如图1所示,首先,根据目前的工程要求和设计标准,设计院制作样品,建筑材料生产厂家根据具体设计内容提供原材料,预制构件厂根据设计构件型号引进材料,成品完成并进行工业生产,然后根据施工的具体进度和施工需要,委托物流公司进行正确的运输,施工公司通过相关的施工机械和技术在对预制构件进行安装,最后由专业的服务团队来完善生产、销售运作管理[6]。

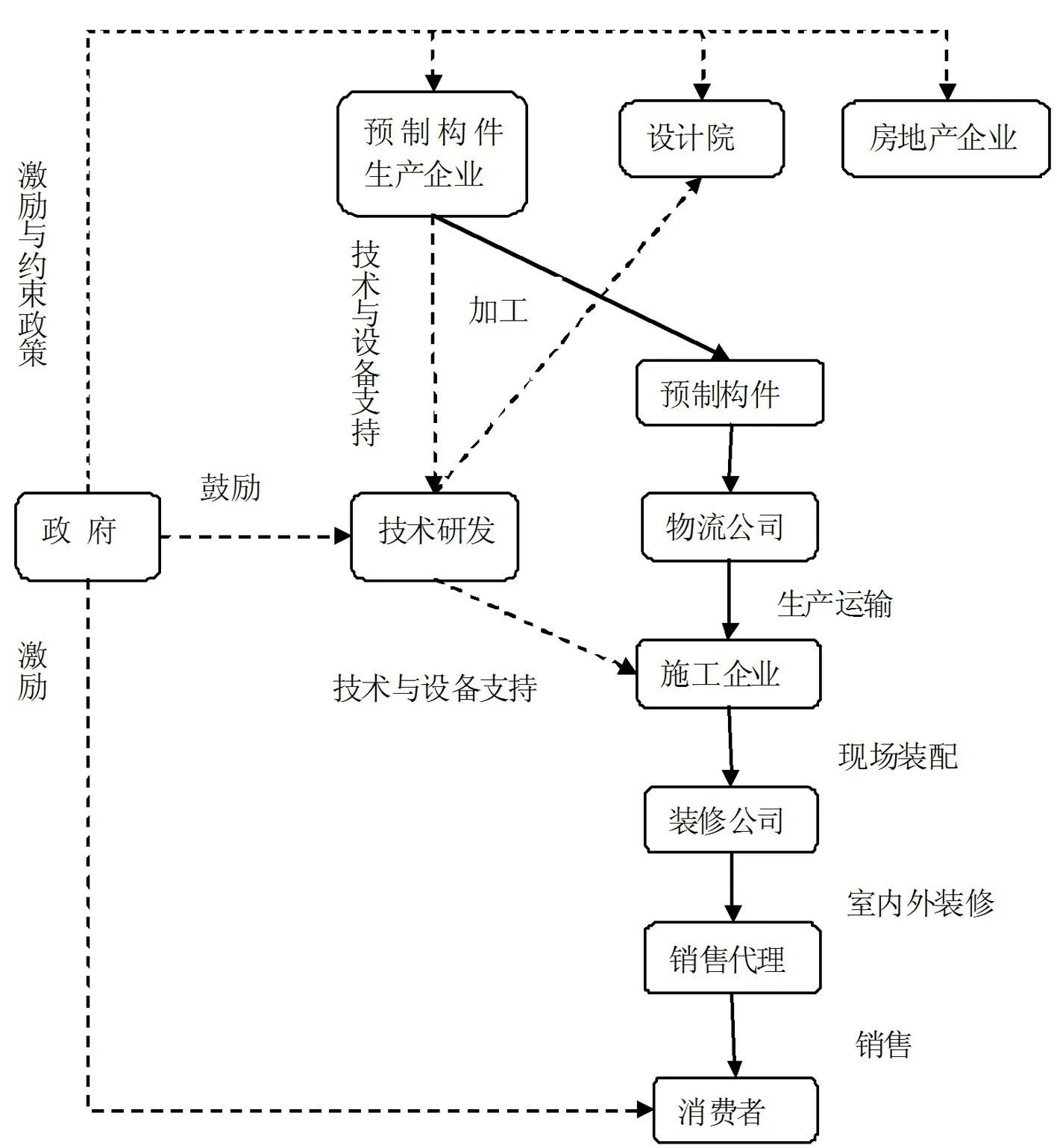
图1 装配式建筑产业链结构模型

1.2 装配式建筑产业链利益分配影响因素

1.2.1 关于产业链利益攸关方的影响因素分析

查阅关于装配式建筑产业链发展的相关文献,发现对于装配式产业链的影响因素主要包括从宏观微观、内部外部等。边晶梅等人主要是从市场环境、产业组织、经济成本、政策法规、人才因素、技术体系对装配式产业链进行因素影响的分析,并通过数据检验证明以上几个因素的重要性[7]。倪国栋等人通过因子分析法、层次分析等方法识别出对装配式建筑产业链的重要影响因素包括企业能力、产业结构、产业成本、企业间协同、市场需要、技术能力、政府管理[8]。王雷等通过建立DEMATEL模型对装配式建筑的影响因素进行定量分析发现影响其发展的重要因素包括政策激励、人才建设、技术体系[9]。从利益攸关方的视角下参考现有的研究成果建立关联图对装配式产业链的收益的影响因素进行分析。

1.2.2 基于传统Shapley值法的影响因素分析

Shapley值法的中心思想就是根据参与者对整个合作联盟的贡献来进行的收益分配,而此处所指的贡献参照的是参与者为合作整体的收益增加的能力,并通过收益增值的比率来进行参与者的收益计算[10]。Shapley值法是合作博弈的一种,对于该值的大小确定依据合作联盟中的“个体力量”,从一般角度看,Shapley值的大小可以看成是局中人在整个博弈中的重要性程度[11]。但是传统的Shapley值法是有一定的局限性,其只考虑了参与者带来的最终收益贡献,没有考虑其资金投入,资金投入量对整个产业链的影响程度是很显著的,因此我们应该把资金投入考虑进去;传统的Shapley值法假设所有的局中人承担相同程度的风险,忽略了各局中人的差异性,收益分配时,应当考虑企业承担风险的情况给予补偿[12];传统的Shapley值法没有对创新的一些激励措施,整个合作联盟的竞争力在于各个成员的竞争力,而对创新特别是技术创新的激励尤是企业提高竞争力的关键,因此应当对技术创新贡献进行奖励[13];传统的Shapley值法没有考虑节点成员的信任程度,以及各节点成员之前是否出现过合作的情况,是否具有一定的偏好性,因此在分配收益的要充分各节点成员之间的信任程度。将风险分担、资金投入、信任程度、技术创新纳入考虑因素,改进Shapley值法,利用改进灰色该关联度对引进的四个因素进行权重的赋值,同时基于TOPSIS法对方案进行综合优化,从而建立产业链分配模型,实现各参与者的收益最大化,从而能够推动整个装配式建筑产业链的稳步发展。

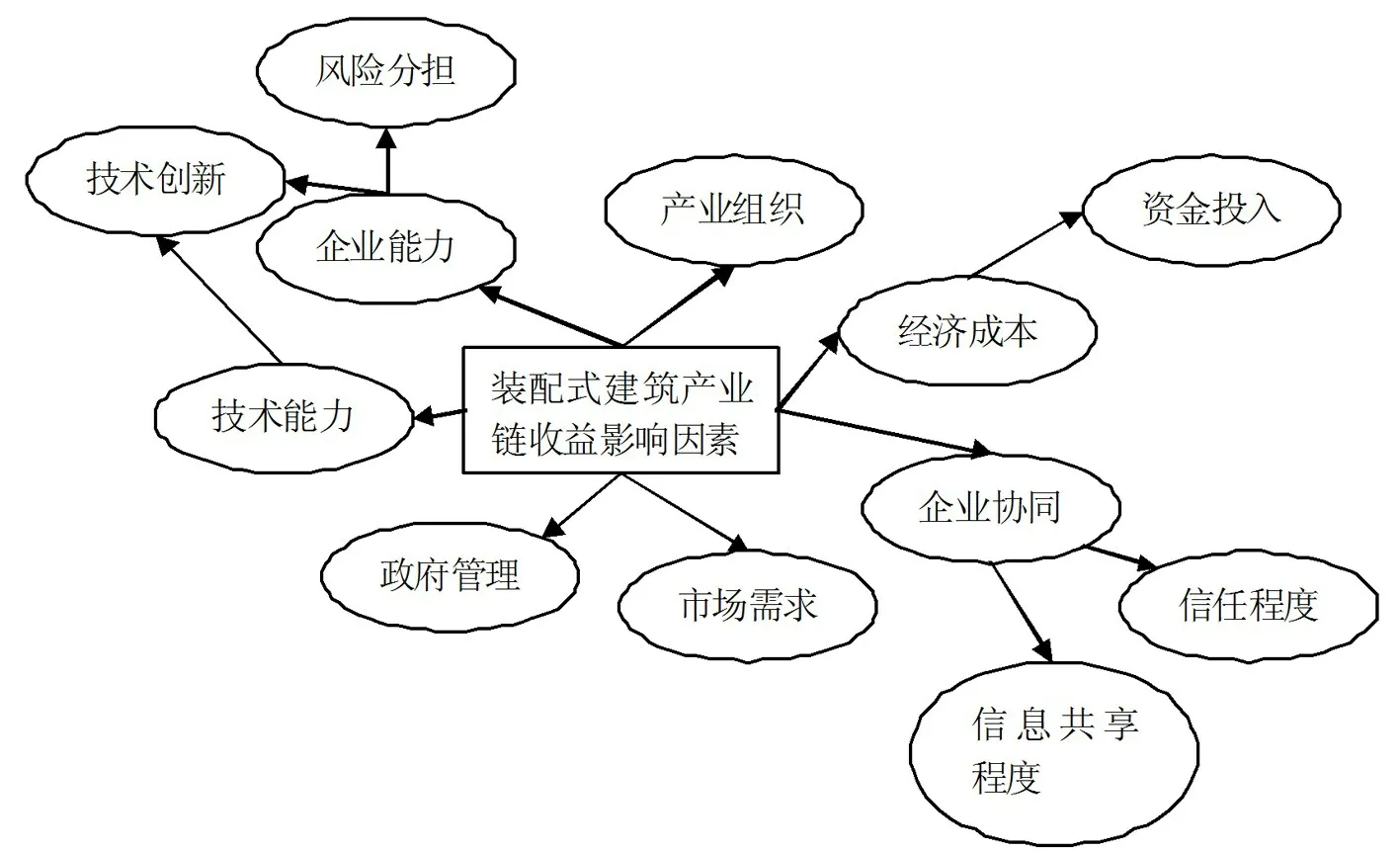
图2 装配式建筑产业链收益影响因素关联图

2 模型建立

2.1 改进Shapley值模型

针对传统的Shapley值法于装配式建筑产业链的缺陷,将风险分担、信任程度、资金投入、技术创新作为影响因素对Shapley值进行修正,在此基础上提出了改进模型,如式(1):

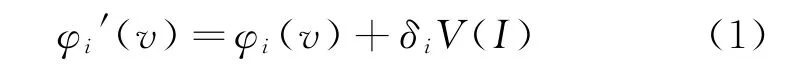
δi为四个影响因素的修正因子系数,V(I)为整个产业链联盟的收益,其中φi(v)运用传统的Shapley值法,即式(2),(3):

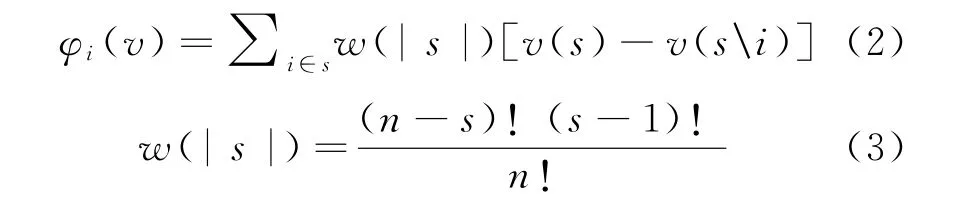
v(s)作为子集s的收益大小,其中s表示的是集合I里面有局中人i的所有子集,v(si)表示的是不包括i整个联盟取得的收益,那么局中人i对整个联盟的贡献就可以表示为v(s)-v(si),其中|s|用来表示整个联盟中利益攸关者的个数。

2.2 模型求解

(1)因子修正矩阵及无量纲化处理

从消除指标间量纲差异出发,对原始的数据进行无量纲化处理。如式(4)所示:

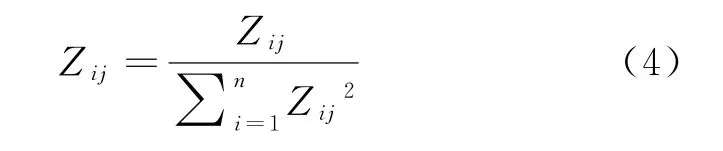
上述公式中i={1,2,...n}是评价对象的集合,j={1,2,...m}是修正因素的集合,a ij是评价对象i对应在每个修正因子j的测度值大小,b ij则表示由原始数据经过无量纲化处理后的数据结果,规范化后的矩阵为

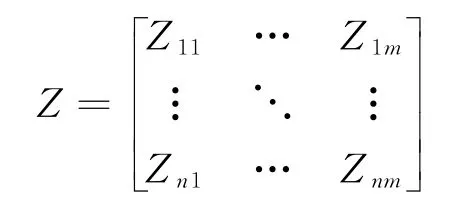
(2)修正因子权重确定

参考文献[14],运用已经改进的灰色关联度进行指标权重的求解,并在此基础上建立确定修正因子权重。

①构建评价指标体系

为构建评价指标体系,现假设评价指标数为n,专家数为m,并且n个专家凭借自身经验对不同指标的权重作出相对应的判断,并用矩阵表示,结果如下:

②确定参考序列

从整个X中挑出一个相对最大的权重值作为所有权重的参考值,并令n个专家的参考权重值均为此值,形成参考列X0

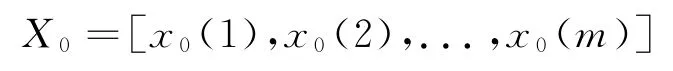
③求各个指标序列X1,X2,...,X n与X0之间距离如式(5):

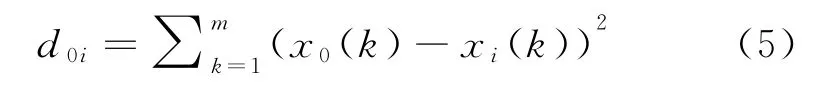
④计算各个指标权重如式(6):

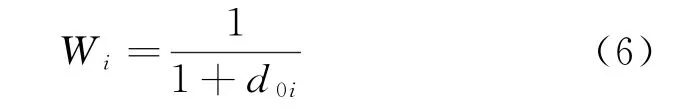
⑤指标权重归一化处理如式(7):

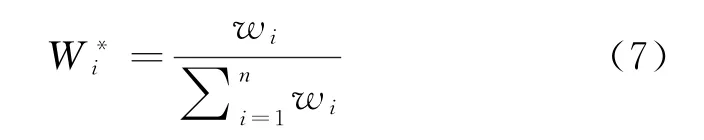
由此可以得到标准化指标权重为式(8):

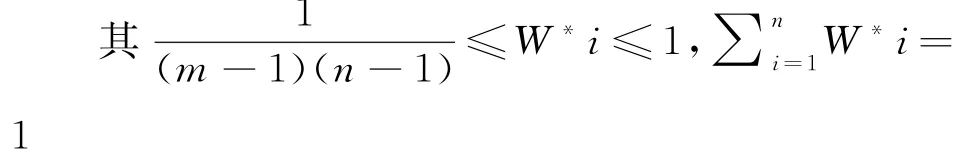
(3)确定产业链分配系数

通过加权的TOPSIS确定装配式产业链的利益分配修正系数,增强数据的利用程度,加大方法的客观性,利用测度计算靠近正理想点的接近度来确定系数。

①确定正理想解与负理想解

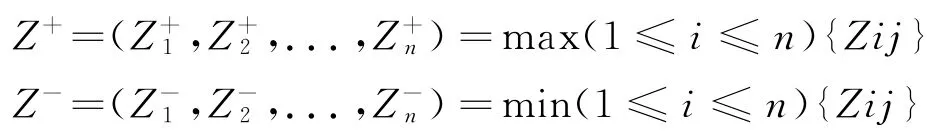
②将归一化的指标权重引入,计算方案到正理想解的加权欧几里得距离如式(9),(10):

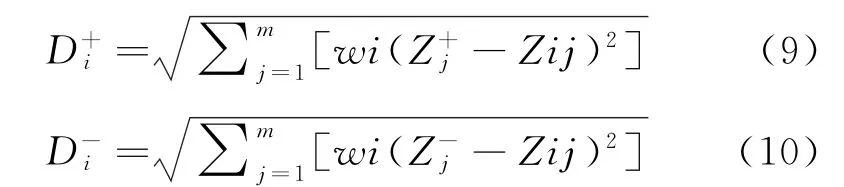
③计算关于正理想解的接近度式(11):

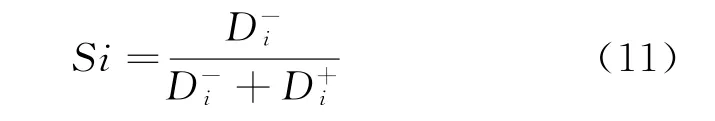
式(11)中i={1,2,3,…,n}

④归一化处理接近度如式(12):

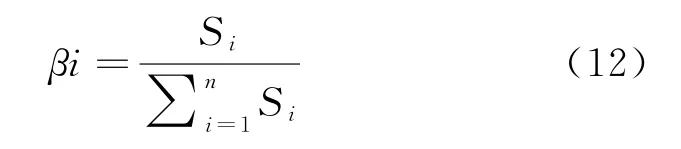
式(12)中i={1,2,3,…,n}

⑤计算归一化接近度与平均度的差,即修正系数

根据传统的Shapley值法,默认局中人的修正系数是相等的,经过归一化处理,均为1/n。本文将引入修正因子进行对比,即式(13):

式(13)中i={1,2,3,…,n}

当δi＞0时,表示该局中人对整个联盟的贡献超过平均的贡献,应当激励该局中人;当δi＜0时,表示该局中人对整个联盟的贡献低于平均的贡献,应当减少其的收益分配,利用扣减其的收益来补偿贡献更大的局中人;当δi=0时,表示该局中人对整个联盟的贡献等于平均的贡献,不改变其的利益分配情况。

2.3 模型可行性证明

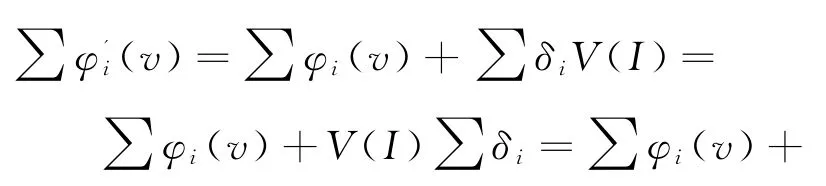
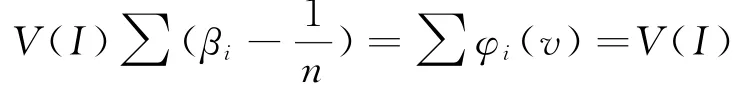
由此可见改进的Shapley值法是符合产业链合作要求的。通过改进分配机制可以有效的激励产业链的各个成员,从而促进产业链的整体发展。

3 案例应用

现有四个成员A,B,C,D构成装配式建筑产业链,成员A代表设计单位,成员B代表构件生产企业,成员C代表运输企业,成员D代表施工企业。根据往年的利润进行推算,单个企业独资经营的利润分别是:V A=15万,V B=60万,VC=15万,VD=110万;两两企业合作经营的利润分别是:V AB=90万,V AC=40万,V AD=160万,V BC=100万,V BD=210万,V CD=150万;三者进行合作经营的利润分别如下:V ABC=130万,VABD=250万,V ACD=190万,V BCD=250万;四个企业进行合作经营的利润是:V ABCD=330万。

3.1 传统Shapley值法分配值计算

由表1及式(2)可得对于成员A的分配利润是41.67万元。同理,可以求得成员B,C,D的分配利润分别是95万元,41.67万元,151.66万元。可以看出按照传统Shapley值法计算的分配利润均高于单独经营的利润,由此可以推出进行产业链合作方式是可行的。

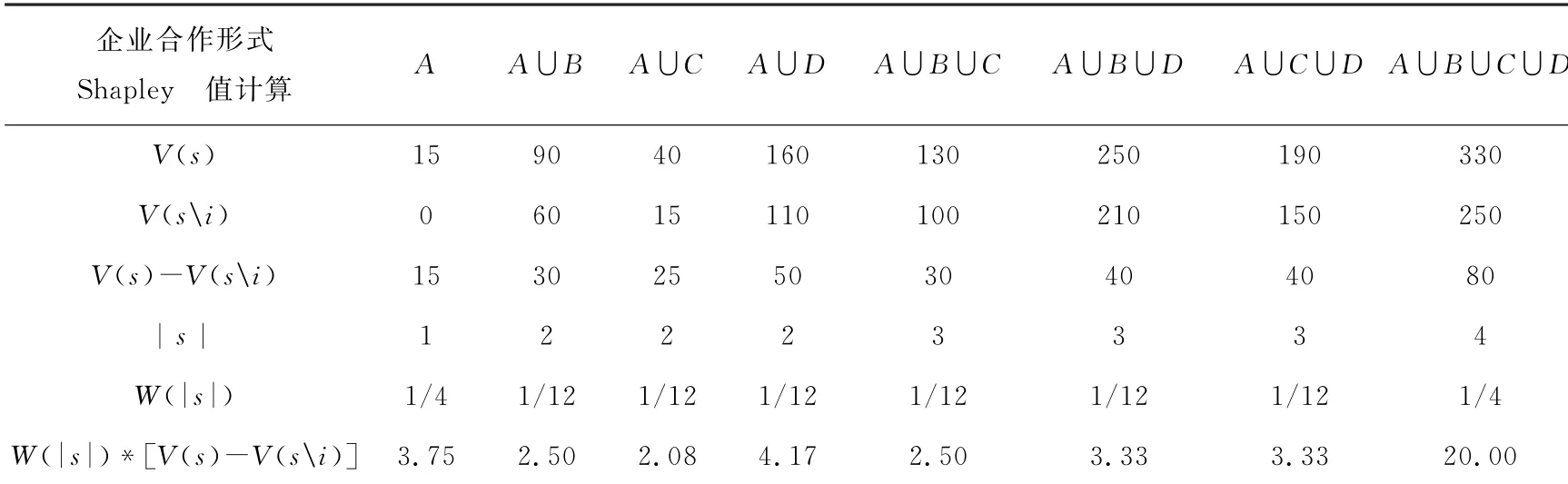
表1 成员A的收益分配过程(单位万元)

3.2 引入修正因子的Shapley值算法

装配式产业链四个参与企业的关于风险分担、信任程度、资金投入、技术创新原始数据情况如表2所示:

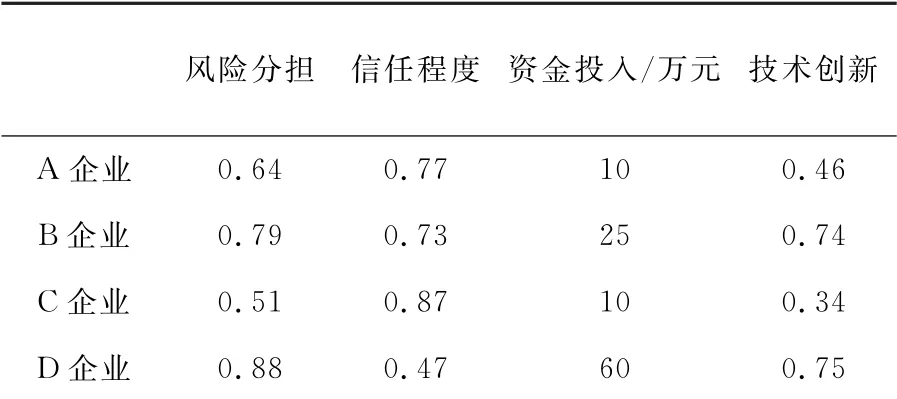
表2 原始数据表

请10名专家对风险分担、信任程度、资金投入、技术创新四个修正因子进行权重判断,判断矩阵如下:

表3 修正因子权重表

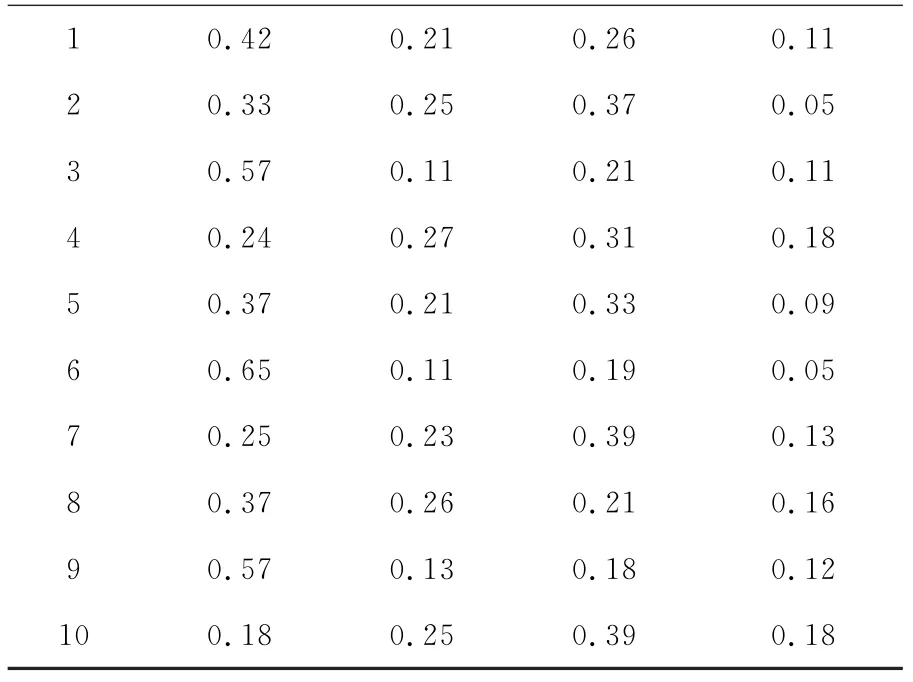
1 0.42 0.21 0.26 0.11 2 0.33 0.25 0.37 0.05 3 0.57 0.11 0.21 0.11 4 0.24 0.27 0.31 0.18 5 0.37 0.21 0.33 0.09 6 0.65 0.11 0.19 0.05 7 0.25 0.23 0.39 0.13 8 0.37 0.26 0.21 0.16 9 0.57 0.13 0.18 0.12 10 0.18 0.25 0.39 0.18

(1)计算各修正因子的指标权重

根据专家评分表对风险分担、信任程度、资金投入、技术创新四个因素的指标权重

①确定参考序列

从专家评分的表中可以看出,权重最大值的X为0.65,即X0=(0.65,0.65,0.65,0.65)

②各个指标与X0之间的距离

根据式(5)得d0=(0.87,0.2,1.4,2.85)

③计算各个指标权重

根据式(6)得W=(0.53,0.83,0.42,0.29)

④归一化处理指标权重

根据式(7)得W*=(0.26,0.4,0.2,0.14)

(2)确定产业链分配系数δi

将原始数据进行无量纲化处理,得到矩阵

①确定正理想解与负理想解

②计算加权欧几里得距离

根据式(9),式(10)可得

③计算关于正理想的接近度

根据式(11)可得

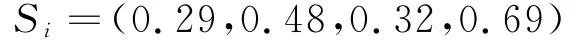
④归一化处理接近度

根据式(12)可得

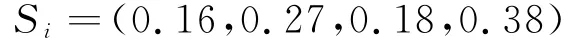
⑤计算修正系数

根据式(13)得

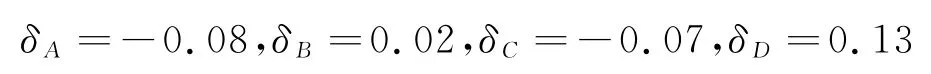
(3)计算修正后的各个企业的分配利润

根据公式(1)得出A,B,C,D四家企业关于利益分配的结果如表4。

表4 利益分配表

(4)计算正负理想点的算子

通过计算关于正理想点与负理想点的算子,从而通过算子大小来衡量靠近正负理想点的距离,计算结果如表5,表6所示。

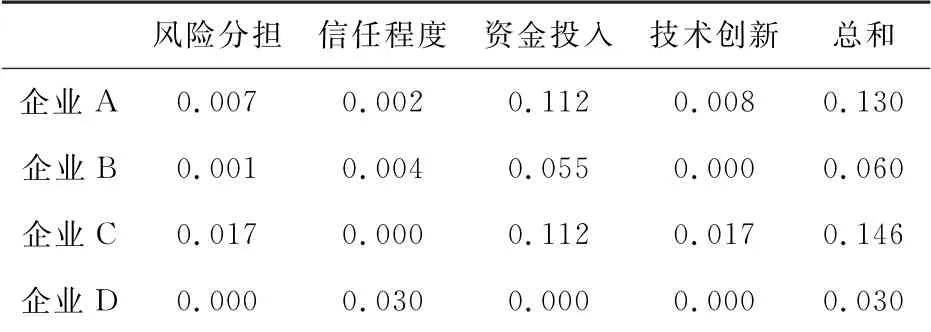
表5 关于正理想点的W i(Z+j-Z ij)2算子

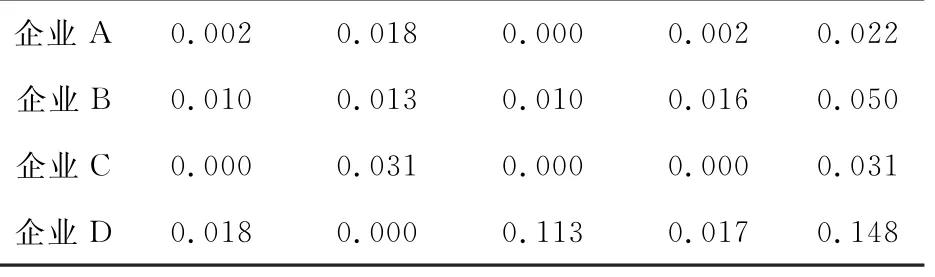
表6 关于负理想点的W i(Z-j-Z ij)2算子

企业A 0.002 0.018 0.000 0.002 0.022企业B 0.010 0.013 0.010 0.016 0.050企业C 0.000 0.031 0.000 0.000 0.031企业D 0.018 0.000 0.113 0.017 0.148

3.3 结果分析

从最终的利益分配表来看,从引进四个因素修正对比传统的方法产生了较大的影响,对于企业A,C来讲收益分配降低了,对于企业B,D来讲收益分配增大了。

从企业A来看δA=-0.08,要将传统方法分配下的值进行削减,从表5及表6可以看出企业A更接近负理想点,主要原因在于其资金投入较少,其风险分担能力以及技术创新能力都不高,所以将企业A减少资金的分配,将减少的利益对其他企进行补贴。

从企业B来看δB=0.02,系数为正,说明在传统分配方法的基础上对企业B增加利益分配,以此对企业进行鼓励。从表5和表6可以看出对企业B进行鼓励的原因在于其技术创新能力较强,风险分担能力也较强,所以应该增加利益分配。

从企业C来看δC=-0.07,系数为负,要削减传统方法分配的值,从表5及表6可以看出企业C关于正理想的算子远大于关于负理想点的,说明企业C更接近负理想点,主要原因在于其风险分担、资金投入、技术创新水平都比较低,虽然信任程度较高,但是无法弥补其他三个因素的缺陷,所以要削减企业C的收益分配来补偿其他的企业。

从企业D来看δD=0.13,其修正系数的值是最大的,说明其在整个装配式产业链中处于主导地位,其贡献水平更高,从表6可以看出其关于负理想点的算子远大于其他值,说明其更接近真理想点,其风险分担能力、资金投入、以及技术创新水平都处于高水平,所以应当对其进行补偿。

4 结 语

研究了装配式建筑产业链的利益分配问题,提出了一种考虑了整个产业链影响因素的分配模型,将风险分担、信任程度、资金投入、技术创新引入收益分配当中。建构的模型能够更充分的考虑各个利益攸关方对整个产业链所做出的贡献,既强调了结果的重要性也说明了合作过程的复杂性和不确定性,同时能为现实中利益攸关方有显著差别的装配式建筑产业链提供一个切实可行的分配方案[15]。因此,引入四个影响因素因子是具有现实意义的。但所构建的模型是基于对利益攸关方各合作模式收益已知的数据基础之上的,没有涉及到各种合作模式的收益预测,这些将是以后研究的一个方向。