Amatrix-based static approach to analysis of finite state machines*

He DENG，Yongyi YAN，Zengqiang CHEN

1College of Information Engineering，Henan University of Science and Technology，Luoyang 471000，China

2College of Artificial Intelligence，Nankai University，Tianjin 300071，China

†E-mail:yyyan@mail.nankai.edu.cn

Abstract:Traditional matrix-based approaches in the field of finite state machines construct state transition matrices，and then use the powers of the state transition matrices to represent corresponding dynamic transition processes，which are cornerstones of system analysis.In this study，we propose a static matrix-based approach that revisits a finite state machine from its structure rather than its dynamic transition process，thus avoiding the“explosion of complexity”problem inherent in the existing approaches.Based on the static approach，we reexamine the issues of closed-loop detection and controllability for deterministic finite state machines.In addition，we propose controllable equivalent form and minimal controllable equivalent form concepts and give corresponding algorithms.

Key words:Logical systems;Finite-valued systems;Semi-tensor product of matrices;Finite state machines;Matrix approaches

1 Introduction

Matrix-based approaches have a wide range of applications in the field of finite state machines(Lu et al.，2018;Chen et al.，2020).For matrix-based approaches，there are two major mathematical model types:the state transition matrix model(TMmodel)(Xu XR and Hong，2013a;Chen et al.，2020)，based on the conventional matrix product，and the matrix model based on the semi-tensor product(STP)model(Xu XR and Hong，2013b;Zhu R et al.，2022).Several representative results are presented(Lu et al.，2017;Yan et al.，2022).For a finite state machine，the TM model is effective for closed-ended issues such as controllability and reachability.However，the computational complexity of the TMmodel is often exponential for the optimal path issue or for finding relevant inputs.The major reason is that some input information is lost in modeling formalism.Fortunately，the missing information can be added to the TMmodel with the help of STP theory，creating the STP model(Xu XR and Hong，2013a;Han et al.，2018).In general，the STPmodel contains all information on a dynamic process，both information of state transitions and that of inputs.Thus，the STP model can solve all issues in the field of finite state machines theoretically.However，a drawback of the STP model is the“explosion of dimension”problem(Yue et al.，2019;Yan et al.，2021);that is，the dimension of state transition matrices in the STP model increases exponentially with increase in the time step.This problem also occurs in the TM model，where the complexity increases polynomially as the time step increases linearly(Xu Qet al.，2021).The“explosion of complexity”is caused by the repeated product of state transition matrices(Cheng and Qi，2010;Yan et al.，2014).One of the major reasons for the repeated product is that state transition processes are always considered as dynamic processes，which implies that each state transition requires a product of the state transition matrix.

Motivated by the“explosion of complexity”inherent in the existing approaches，in contrast to traditional matrix-based approaches，we propose a static matrix-based approach，which relies on the structure of a finite state machine itself rather than its dynamic process，thus avoiding the“explosion of complexity.” Based on the static approach，we reexamine the issue of closed-loop detection in deterministic finite state machines.By the fact that all states in a closed loop are mutually controllable，we present the definitions and algorithms of a controllable equivalent form and a minimal controllable equivalent form.With a static view of the closed loop，the two-state controllability issue can be resolved only once，by matrix division，making use of our algorithms in the best case.

2 Preliminaries

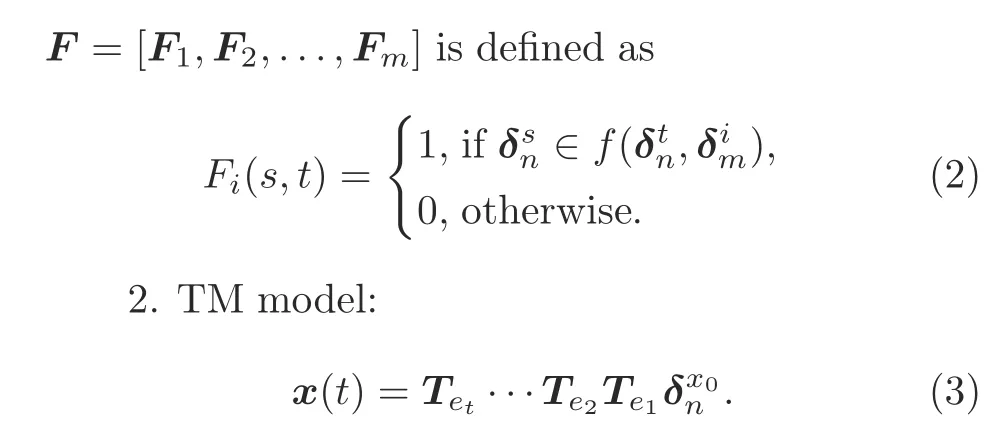
Eqs.(1)and(3)are standard matrix models in that they construct the state transition matrices，~Fin the STP model andT e i(1≤i≤t)in the TM model，to describe the dynamics ofA.Note that we are more interested in the outcome of a state transition than in the inputs that can cause the transition.Therefore，we modify Eq.(3)as

3 Main results

3.1 Static approach for detection of closed loops

The closed loops，the core point of this paper，are proposed in this subsection.

Definition 1For a deterministic finite state machine(DFSM)M=(X=Δn，E，f，x0)，a state setXs⊆Xis called a single closed loop，if for allx∈Xs，

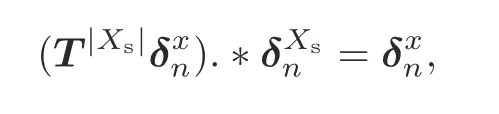
where“.*”denotes element-wise multiplication.

Although Definition 1 is an accurate description，it is not less complex than the repeated matrix products in Eqs.(1)and(3).Thus，we give the following definition of a weak version:

Definition 2For a DFSMM=(X=Δn，E，f，x0)，a state setXs⊆Xis called a single closed loop，if

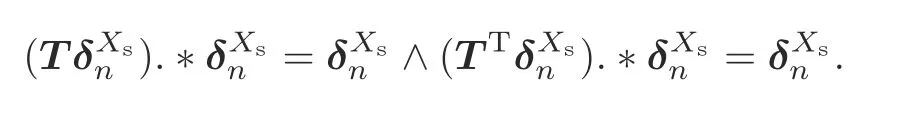
Note that Definition 2 is not strictly a sufficient condition，but it can be applied to the results presented in this paper and has time complexityO(1).

Algorithm 1 Finding closed loops in a DFSM at‖T‖=0 1:Construct T.2:The set of all closed loops is C={Ψ(x)|(T-I n×n)x=0∧(T-I n×n)x*/=0}，where x*∈2x.

Next，we consider more general cases and begin with‖T‖=1.

Lemma 2For any DFSMM=(X=Δn，E，f，x0)at‖T‖=1，if a state setXs⊆Xis a single closed loop，then

Lemma 2 is also a necessary condition.To find all single closed loops at‖T‖=1，the idea is to first find all possible single closed loops by the necessary condition，and then to use Definition 2 to determine which ones are single closed loops.From Lemmas 1 and 2，one way to find single closed loops is given in Algorithm 2.Note that Algorithm 2 cannot find compound closed loops.The algorithm for solving compound closed loops is stated later.

Lemma 3For any DFSMM=(X=Δn，E，f，x0)at‖T‖=2，if a state setXs⊆Xis a single closed loop，then

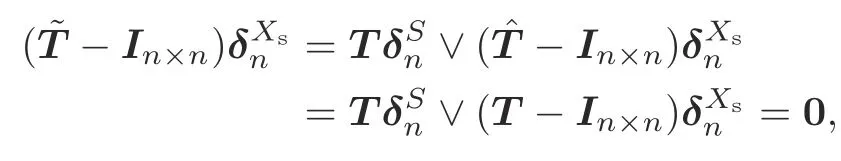
whereS={i||Ψ(coli(T))|＞1}，is described in Lemma 2，andˆTis defined as

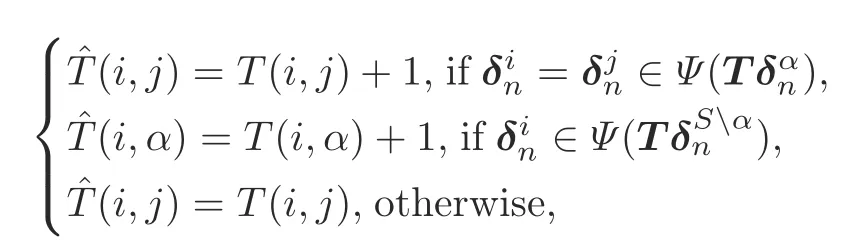
whereα∈S.

Algorithm 2 Finding all single closed loops for M=(X=Δn，E，f，x0)at‖T‖=1 1:Construct˜T by computingα.2:Compute X s={x|(˜T-I n×n)x=Tδαn}.3:Apply Definition 2 to X s.4:Apply Algorithm 1 to M.

Algorithm 3 Findingθαfor M Input:T，α，S:={i||Ψ(col i(T))|＞1}，D:=Sα，θα:={α}，L:=∅Output:θα 1:whileθα∪L/=S do 2: T*:=T 3: Y:=Ψ(x)|(T-I n×n)x=0 4: for i∈D do 5: for δjn∈Ψ(Tδin)do 6: if j/∈θαthen 7: T*(:，j):=0 8: T*(α，j):=T*(α，j)+1 9: for δkn∈Ψ(Tδin)δjn do 10: T*(k，j):=T*(k，j)-1 11: end for 12: else 13: T*(j，j):=T*(j，j)+1 14: end if 15: end for 16: T*(α，α):=T*(α，α)+1 17: if(T*-I n×n)x=Tδθαn has a solution set C and|{k|k∈C∧k∩Y=∅}|=|Ψ(Tδin)|then 18: BREAK:θα:=θα∪{x i}19: else 20: L:=L∪{x i}21: end if 22: end for 23:end while

From Corollary 1，Lemma 4，and Algorithm 3，one way to find all single closed loops for any DFSM is given in Algorithm 4.Algorithm 4 has time complexityO(|S|)and space complexityO(n2).

Remark 1From Algorithm 4，it is easy to find that the reason why Definition 2，as the weak version of Definition 1，is applicable in this paper-we traverse all bifurcation states and detect the existence of a single closed loop at each bifurcation state.

3.2 Static approach for a controllable equivalent form

Clearly，for any DFSM，all states in a single closed loop are mutually controllable.Therefore，we can combine a single closed loop into a single“aggregate”state without changing the controllability of the whole DFSM.We give the following definition:Definition 4 Consider a DFSMM=(X=Δn，f m，x0).A=(X=Δa，f a，x0)is called a controllable equivalent form ofM，if there exists a functionf:Δa→2Δn，such that

The functionfshows the correspondence between the new statey i∈Δaand the original statex i∈Δn，and is called a controllable equivalent function.We are used to expressing a DFSM in terms of state transition matrices.One way to obtain a controllable equivalent form in the TMmodel is stated in Algorithm 5.Note that Algorithm 5 can be considered as a proposition for the controllable equivalent form.Therefore，we present a part of the MATLAB code to emphasize this point.Algorithm 5 has time complexityO(l)and space complexityO(n2)，wherelis the number of single closed loops in the DFSM.Given a setS/=∅of which the elements are sets，π(S)is defined asπ(S)=(Sx i，x j)∪(x i∪x j)wherex i，x j∈Sandx i∩x j/=∅.For a DFSM，the controllable equivalent form is often not unique.In practice，we are more concerned with the DFSM with the fewest states.Thus，we give the following definition:

Algorithm 4 Finding all single closed loops for M Input:T， W := ∅， H := ∅， D := ∅， S :={i||Ψ(col i(T))|＞1}Output:W M 1:while S/=D∪H do 2: α∈SH 3: Apply Algorithm 3 to obtainθα 4: if|θα|=1 then 5: D:=D∪θα 6: else 7: H:=H∪θα 8: end if 9: C:=images/BZ_109_458_2647_484_2680.pngimages/BZ_109_851_2647_877_2680.pngx■■■■(■T-I n×n)x=TδSn 10: for i∈C do 11: if(T i).*i=i∧(T T i).*i=i then 12: W:=W∪{Ψ(i)}13: end if 14: end for 15:end while 16:C*:={Ψ(x)|(T-I n×n)x=0∧(T-I n×n)x*/=0(x*∈2x)}17:W:=W∪C*

Algorithm 5 Controllable equivalent form of M Input:T，W M，T*:=[]，T°:=[]Output:T°is the TM model of the controllable equivalent form of M;the controllable equivalent function f is defined as y i=f(x i)=Ψ(col i(T*))1:for i∈W M do 2: a=minimages/BZ_109_1503_1332_1519_1365.pngfindimages/BZ_109_1584_1332_1600_1365.pngδin））3: 1n=ones(n，1)4: b=1n-δin 5: T*=diag(b)6: T*(:，a)=δin 7: T*(:，all(T*==0))=[]8: A=((T.′)*T*)9: A(:，a)=A(:，a)-δin 10: T°=((A.′)*T*)11:end for

To obtain the minimal controllable equivalent form，compound closed loops must be processed.There are two ways to solve the compound closed loops:the circulation method and the virtual state method.The circulation method detects a single closed loop and combines the states therein repeatedly.Algorithm 6 is proposed with the circulation method and has time complexityO(c)and space complexityO(n2)，wherecis the maximum number of single closed loops nested in a compound closed loop.

Algorithm 6 Finding all closed loops and the minimal controllable equivalent form for M Input:T，T min:=T，W*:=∅Output:T°min is the TM model of the minimal controllable equivalent form;W*contains all closed loops in M 1:repeat 2: T min:=T°min 3: Apply Algorithm 4 to obtain W min for T min 4: Apply Algorithm 5 to obtain T°min for T min 5: W*:=W*∪W min 6:until T°min=T min

Remark 2Note that Algorithm 6 obtains all closed loops in a DFSM while obtaining the minimal controllable equivalent form. Although its efficiency decreases with an increase in the number of compound closed loops，it is still valuable when performing distributed simplification of large networks of DFSMs.

3.3 Static approach for controllability

In this subsection，we reconsider the issue of controllability with the help of closed loops.

Lemma 5Consider DFSMM=(X=Δn，E，f，x0).Ifx a∈Δnis controllable tox b∈Δn，then there exists a closed loop containingx aandx binMκ，whereMκis defined as

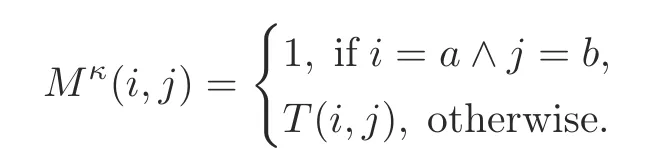
ProofBy contradiction，assume that there is no closed loop.We then have thatx aandx bare either unreachable to each other or reachable in one direction.Note thatMκ(a，b)=1 implies thatx bis controllable tox a.Hence，x ais not controllable tox b，and a contradiction holds.

To cope with the problem of repeated matrix product，we now present a procedure that virtualizes a connection from the goal state to the start state，and uses the idea of closed loops with a virtual state method.This procedure is called the virtual connection method and is reported in Algorithm 7.The so-called virtual state method refers to adding a virtual state to each closed loop，to destroy the structure of the closed loops that are nested in compound closed loops. At this time，the compound closed loops become single closed loops.More precisely，givenM=(X=Δn，E，f，x0)andQ(Q⊆X)，the TM model with the virtual state method forQ，denoted byT V(Q)，is defined as

Algorithm 7 Two-state controllability with the virtual connection method for M=(X=Δn，E，f，x0)Input:T， goal state x b， start state x a， S :={i||Ψ(col i(T))|＞1}1:T(x a，x b)=1 2:Construct T V(S)3:Construct■T V(S)whereαis specified as the start state x a 4:C:=｛Ψ(x)■■■■(■T V(S)-I(n+|H*|)×(n+|H*|))x=T V(S)δS n+|H*|∧(T x).*x=x∧(T T x).*x=x｝5:if C/=∅then 6: BREAK:x a is controllable to x b 7:else 8: BREAK:x a is not controllable to x b 9:end if

4 An illustrative example

Example 1ConsiderA=(X，E，f，x0)depicted in Fig.1，whereX={1，2，3，4，5，6，7，8，9，10}，x0={1}，E={a，b}，and transition functionfis represented by labeled arrows.

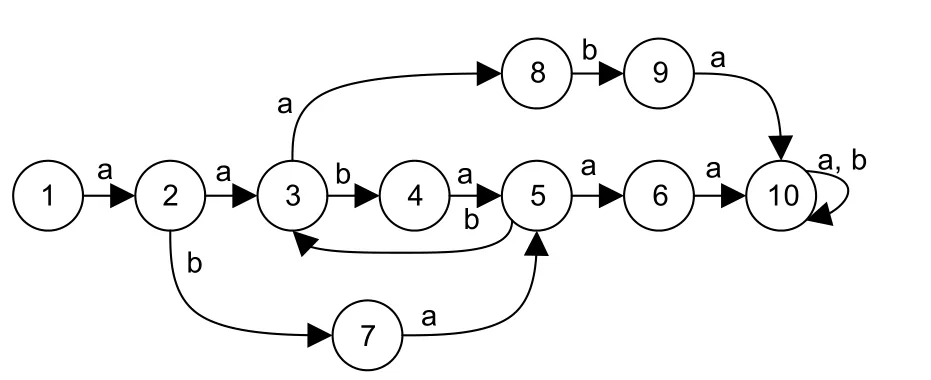
Fig.1 DFSM A

1.Apply Algorithm 3 to obtainθαwhereα=5，and apply Algorithm 5 to obtainθ.

The TM model ofAis as follows:

Then we haveS={2，3，5}，D={2，3}，θα={5}，andY={10}.Fori=3∈S，T*is constructed as

2.Apply Algorithm 6 to obtain the minimal controllable equivalent form.

According to the controllable equivalent functionf(x i)=Ψ(coli(T*))and the notationy i=f(x i)=x′i，we have 1′={1}，2′={2}，3′={3，4，5}，4′={6}，5′={7}，6′={8}，7′={9}，8′={10}.The minimal controllable equivalent form is shown in Fig.2.

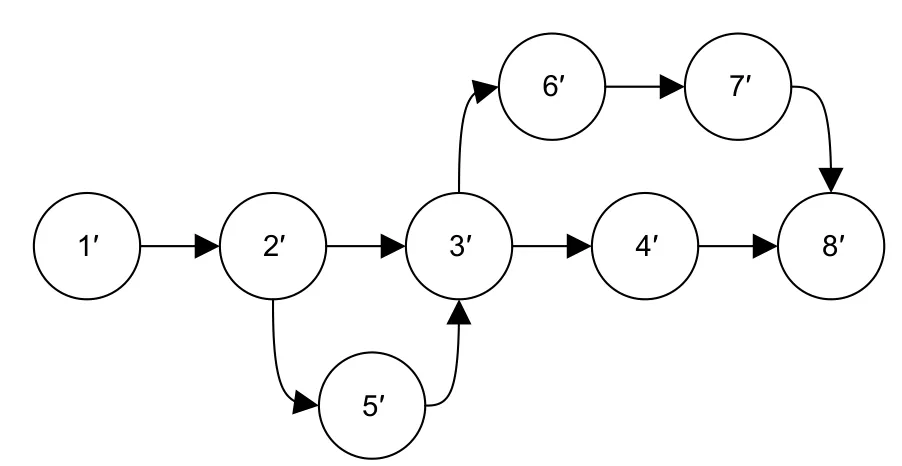
Fig.2 The minimal controllable equivalent form of A in the TM model

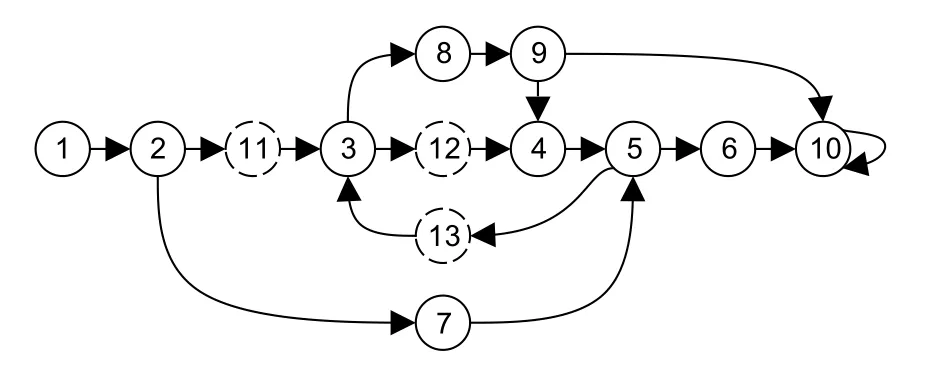
Fig.3 The modified TM model of A with the virtual states

5 Concluding remarks

A matrix-based static approach for detection of a closed loop has been proposed.Based on the static view，we propose the definitions of the controllable equivalent form and minimal controllable equivalent form.The static approach is then extended for controllability and eliminates the“explosion of complexity”problem inherent in the existing approaches.For the issues mentioned in this work，the implementation of our algorithms is much simpler than that of algorithms designed from the dynamic process perspective.

Contributors

He DENG conceived the concept，designed the research，and drafted the paper.Yongyi YAN and Zengqiang CHEN supervised the research，helped organize the paper，and revised and finalized the paper.

Compliance with ethics guidelines

He DENG，Yongyi YAN，and Zengqiang CHEN declare that they have no conflict of interest.