Adaptive neural network based boundary control of a flexible marine riser systemwith output constraints*#

Chuyang YU，Xuyang LOU‡，Yifei MA，Qian YE，Jinqi ZHANG

1Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education)，Jiangnan University，Wuxi 214122，China

2College of Internet of Things Technology，Wuxi Institute of Technology，Wuxi 214121，China

3Wuxi Good Cloud IoT Technology Co.，Ltd.，Wuxi 214196，China

†E-mail:sunrise_ycy@stu.jiangnan.edu.cn;Louxy@jiangnan.edu.cn

Abstract:In this study，we develop an adaptive neural network based boundary control method for a flexible marine riser system with unknown nonlinear disturbances and output constraints to suppress vibrations.We begin with describing the dynamic behavior of the riser system using a distributed parameter system with partial differential equations.To compensate for the effect of nonlinear disturbances，we construct a neural network based boundary controller using a radial basis neural network to reduce vibrations.Under the proposed boundary controller，the state of the riser is guaranteed to be uniformly bounded based on the Lyapunov method.The proposed methodology provides a way to integrate neural networks into boundary control for other flexible robotic manipulator systems.Finally，numerical simulations are given to demonstrate the effectiveness of the proposed control method.

Key words:Marine riser system;Partial differential equation;Neural network;Output constraint;Boundary control;Unknown disturbance

1 Introduction

As an important part of the development of deep-sea oil and gas field systems，marine riser has become particularly noticeable with its brand-new form，dynamic characteristics，and high technology(Zhao et al.，2019).In addition，marine risers with flexible structures are much lighter and have better flexibility and deformations than the ones with ordinary rigid structures(Gao et al.，2014;He W et al.，2018).However，due to the distinct traits of the flexible structure and unknown disturbances，marine riser vibrations will damage the system.Therefore，control of vibrations and disturbances of flexible marine risers in a drilling platform is of practical importance.

Due to the material properties and strong nonlinear characteristics such as external disturbances and model uncertainty，ordinary mathematical models are not suitable for describing marine riser systems.Thus，the Hamilton principle is used to represent marine riser system dynamics，which is described by the distributed parameter system(Ma et al.，2021). Because the system state includes space and time variables，the dynamics of the system is formed by partial differential equations(PDEs)(Zhang XP et al.，2005;Smyshlyaev et al.，2009).There are also many control methods to stabilize vibrations in flexible marine risers(Zhao et al.，2020;He XY et al.，2021).Due to the limitations of the system structure，for a series of flexible structures including marine risers，the control input is imposed on the boundary. For example，Ge et al.(2010)proposed an early boundary control method for a coupled，nonlinear，flexible marine riser.In Do and Pan(2008)，a boundary controller was designed to suppress vibrations with control input on top of the marine riser.

Marine riser systems applied in the actual production are always accompanied by many unknown nonlinear disturbances(He W et al.，2011;Herrera et al.，2017).The existence of these nonlinearities leads to instability of the dynamic system，and it is difficult to obtain an accurate model of these nonlinear disturbances.Elimination or approximation of these nonlinear disturbances is the key in current research on the stabilization of flexible marine riser systems.For instance，Zhao et al.(2020)constructed a new robust adaptive vibration control strategy and proposed an update law for the riser system.Wang JW et al.(2019)proposed an adaptive boundary feedback controller to ensure that the closed-loop system is exponentially stable.Nevertheless，the solution to vibration control of a marine riser system with unknown disturbances is seldom considered.

Many industrial systems may face various problems.In He W et al.(2015)and Wan et al.(2021)，top tension constraints for a flexible marine riser were investigated，but the output constraints of the top slope were not taken into consideration.Excessive output may cause damage to the system hardware.For instance，in marine riser systems，excessive bending of the riser may cause damage to the riser.Meanwhile，because the marine riser is usually very long，the larger the output slope is，the farther the drilling platform deviates from the center of the riser.Therefore，it is necessary to provide output constraints to protect marine riser systems.

Nowadays，many studies used observers to deal with unknown disturbances(Jiang et al.，2015;Guo et al.，2018).Although the observer does not need to know the specific form of the disturbances，it may make obtaining parameters to be difficult.Hence，due to technology improvements，the radial basis function neural network(RBFNN)has received much attention from researchers in control theory(Chen et al.，2020;Xue et al.，2020;Wang N et al.，2021). Because it has a simple structure，strong nonlinear approximation ability，and good generalizability，it has been used in many fields such as pattern classification，function approximation，and data mining(Yin et al.，2020;Yu et al.，2020).He W et al.(2017)designed a neural network controller to suppress vibrations of a flexible robot manipulator with an input dead zone.The purpose of introducing the neural network is to eliminate the dynamics of the mechanical arm and influence of the input dead zone.To the best of our knowledge，little research has been conducted in applying the RBFNN for robust vibration suppression of a flexible marine riser system with boundary disturbances.Hence，we present an RBFNN with the marine riser system control problem to approximate its existing nonlinear disturbances and to solve the model uncertainty problem.

The aim of this research is to design an adaptive neural network based boundary control method to suppress the vibrations of marine riser systems with unknown disturbances and output constraints.The main contributions of this paper are as follows:

1.An adaptive neural network based boundary controller is developed to deal with the bounded distributed disturbances，unknown boundary disturbances，and vibration problem.

2.The proposed controller achieves uniform boundedness of the state variables and maintains the output constraints due to the barrier term.

3.Numerical simulation analysis in various scenarios illustrates the effectiveness of the proposed strategy.

2 Problem formulation

Consider the typical marine riser system shown in Fig.1.Using the Euler-Lagrangian equation and Hamilton principle，the marine riser system can be obtained as the following governing equation:

with∀t∈[0，∞).The parametersρ，T，E I，M，andLof this riser denote the mass per unit length，tension，bending stiffness，mass of the tip payload，and length of the marine riser，respectively.f(x，t)represents the distributed disturbances.g(d(t))∈R withd(t)=[y t(L，t)，y x(L，t)]Trepresents the unknown nonlinear disturbances given byg(d(t))=d1(y t(L，t))+d2(y x(L，t))+d3(t)，which is on the tip boundary of the riser and includes the velocity and angle of this riser.Boundary condition(3)describes the performance of the marine riser on boundaryL.In addition，both the nonlinear functiong(d(t))and the control inputu(t)act on the top end.

Remark 1Ocean currents may cause disturbances to the marine riser.Such disturbances can be regarded asf(x，t).However，there are more complicated friction currents on the surface.The effect of prevailing wind on the friction force of the surface and the pressure exerted by the wind on the windward surface of the wave will affect the riser platform.Such environmental disturbances can be regarded asg(d(t)).At the same time，the marine riser platform should not float too far，so such a constraint needs to be limited.

The main objective of this study is to control vibrations of a flexible marine riser system with barrier constraints.We need the boundary outputy x(L，t)to satisfy the constraints，that is，|y x(L，t)|＜l0(l0∈R+can be regarded as the slope of the tip boundary).The impact of unknown disturbances needs to be considered.Fig.1 shows a typical marine riser structure.

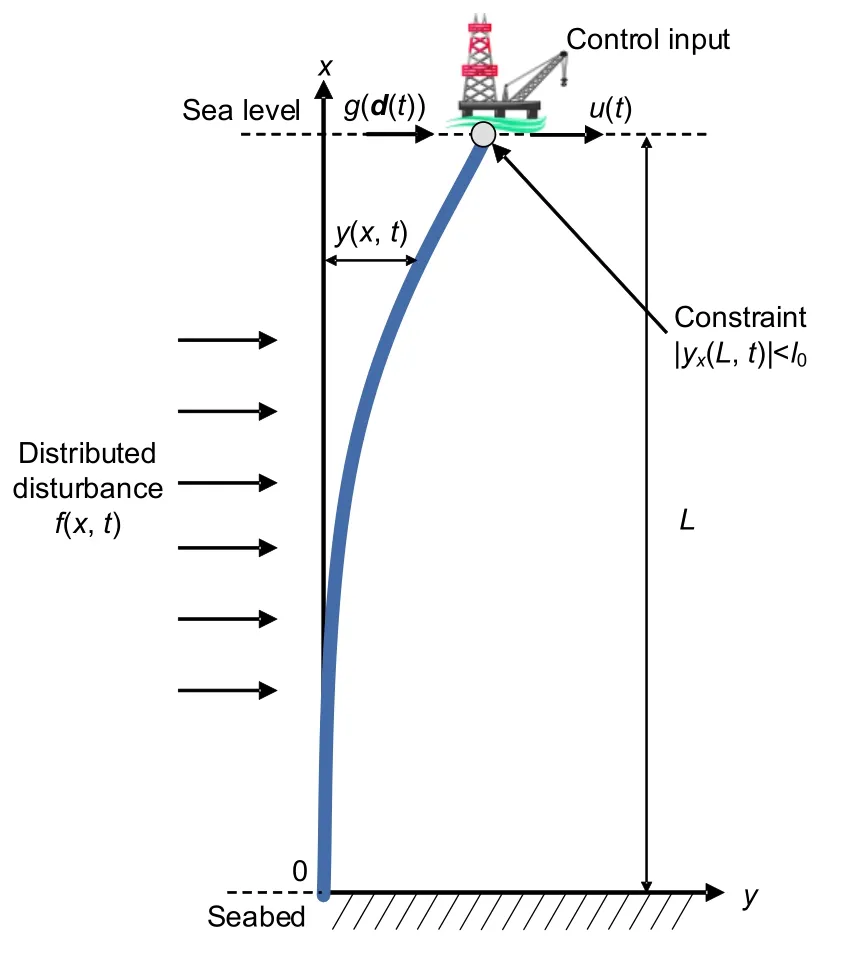
Fig.1 A typical marine riser system

Sinceg(d(t))is unknown，we approximate this unknown function in the form of an RBFNN:

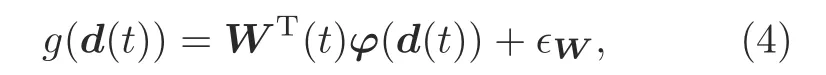
whered(t)∈Rpis the input vector andpis the number of neurons in the input layer.W(t)∈Rqis the weight vector andqis the number of neurons in the hidden layer.∈Wis a neural network estimation error.φ(d(t))∈Rqis the output of the hidden layer，in which the Gaussian function is shown as

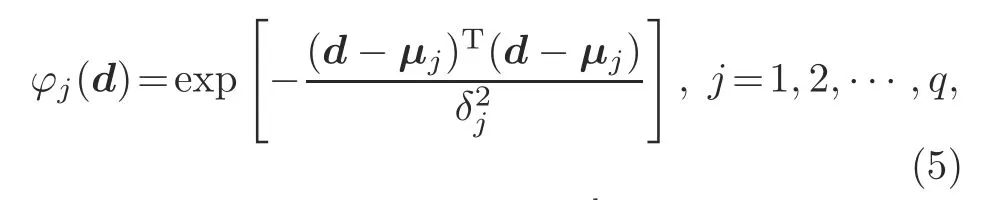
whereμjis the center of thejthhidden unit andδjis the width of thejthhidden unit.

By applying the universal approximation property of the RBFNN(Zhang JH et al.，2016;Guo et al.，2018)，we can obtain

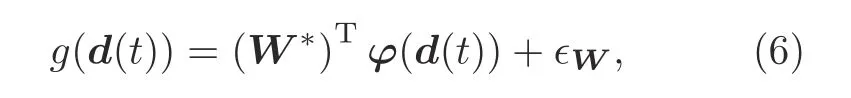
whereW*is the ideal weight vector.

Remark 2The effect of using RBFNN to solve the problem depends on the choice of the radial basis function.Both the center point and the width of the radial basis will affect the neural network.

Before carrying this research further，the following assumption is required:

Assumption 1We assume that there exists a constant¯f∈R+satisfying|f(x，t)|≤¯f，∀(x，t)∈[0，L]×[0，∞);that is，f(x，t)is bounded.

Remark 3It is noted that the energy of the distributed disturbancef(x，t)is finite.Hence，it is reasonable to assume that the disturbance is bounded.Next，we introduce two lemmas to pave the way for the stability analysis:

Lemma 1(Rahn，2001) Letω1(x，t)∈R andω2(x，t)∈R with(x，t)∈[0，L]×[0，+∞).For anyδ＞0，the following inequality holds:

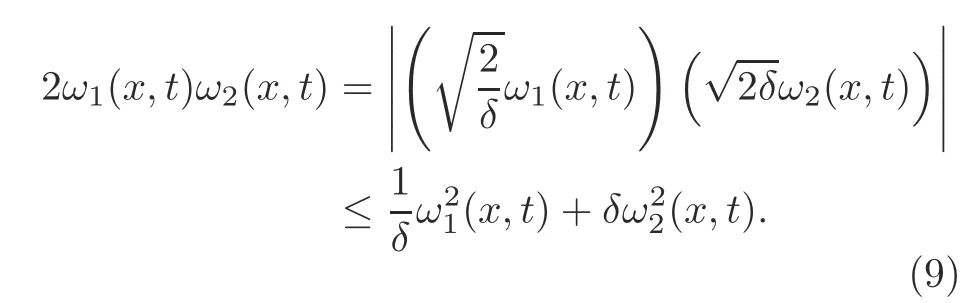
Lemma 2(Hardy et al.，1952;Rahn，2001) Letω(x，t)∈R with(x，t)∈[0，L]×[0，+∞).Ifω(0，t)=ωx(0，t)=0，∀t≥0，then the following inequalities hold:

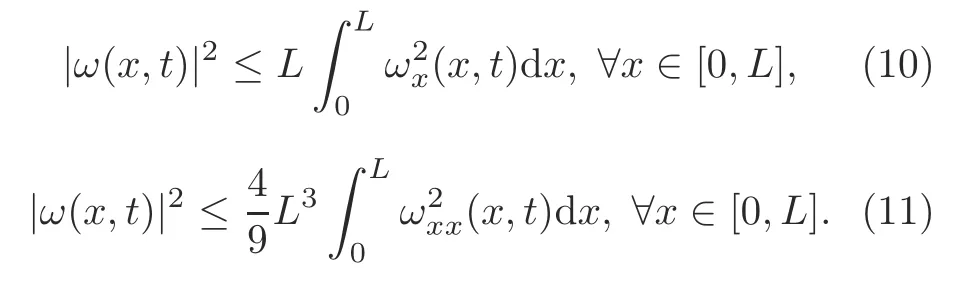
3 Main results

In this section，a boundary control method is proposed to suppress vibrations of the flexible marine riser，while the drilling platform and the riser are kept near the center under disturbances.The boundary controlleru0(t)is designed to guarantee that the constraint of the boundary output can be constructed as follows:

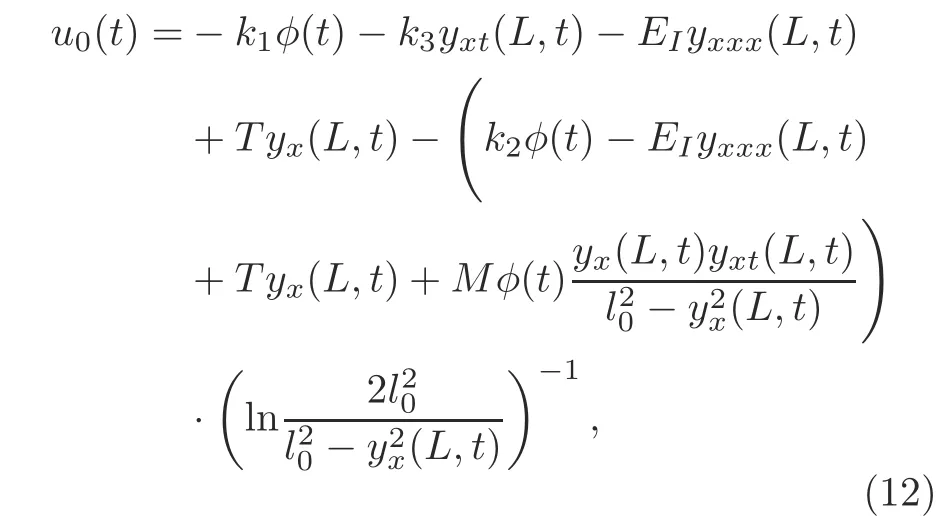
wherek1，k2，andk3are control gains to be determined，andφ(t)is defined as

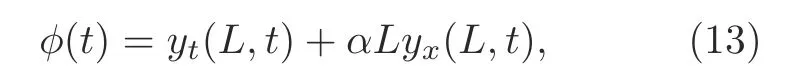
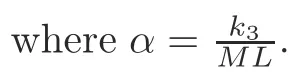
Remark 4The required states in the controller can be measured by sensors.y x(L，t)can be measured by a tilt angle sensor andy xxx(L，t)can be measured by a shear force sensor.Then，we can obtainyt(L，t)andy xt(L，ts)by difference operation.

Because the unknown disturbanceg(d(t))may exist at the boundary，which should be approximated，an adaptive neural network based boundary controlleruNrealized by RBFNN is designed as

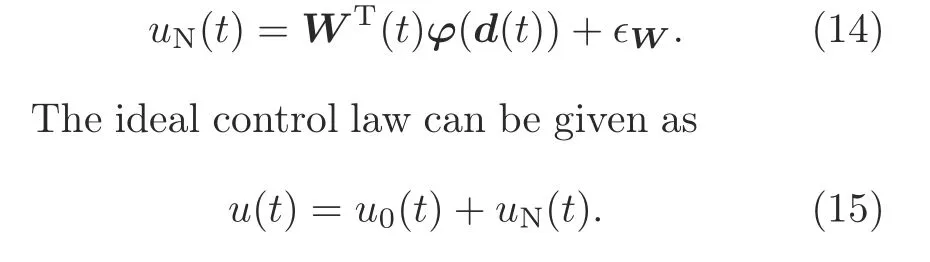
This controller is proposed to track the unknown functiong(d(t))and can ensure stability when output constraints and unknown disturbances exist.However，due to the existence of∈W，the exact value ofuN(t)is difficult to obtain.Therefore，the following neural network based controller is designed:

whereβandk4are gains that need to be designed.

Diagram of the proposed control strategy is presented in Fig.2 to illustrate the overall design of the flexible marine riser system.

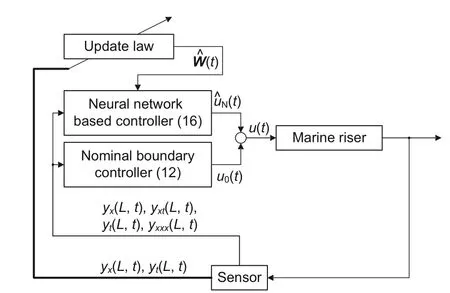
Fig.2 Diagram of the proposed control strategy

3.1 Well-posedness of the controlled system

In this subsection，the well-posedness analysis is given.To facilitate the analysis，combining control input(17)，the closed-loop system can be expressed as

Define a Hilbert spaceH=H2(0，L)×L2(0，L)×R×Rq.The inner product is defined by

whereZ i=(f i(x)，e i(x)，h i，l i)T∈H，i=1，2.It is easy to prove that the inner product(Eq.(20))is equivalent to the natural inner product onH.

Define an operator A as

3.2 Stability analysis

In this subsection，the stability of the system is discussed using the Lyapunov theory.

Consider the following Lyapunov function:

whereV1(t)，V2(t)，V3(t)，andV4(t)are the energy term，barrier term，crossing term，and auxiliary term，respectively.They are defined as

Theorem 2Consider the flexible marine riser system(1)-(3)with external disturbances.Under the boundary controller(17)consisting of the nominal boundary controller(12)and neural network based controller(16)，if the parameters satisfy

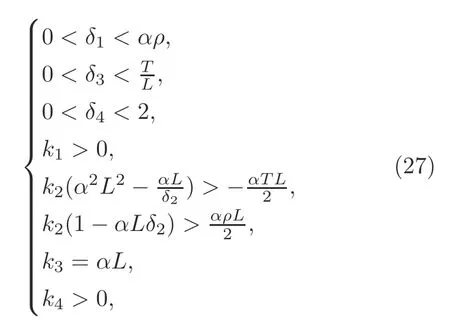
whereδ1，δ2，δ3，δ4，andβare positive constants，then the following can be concluded:

(1)The statey(x，t)is uniformly bounded;

(2)Given that the initial condition satisfies-l0＜y x(L，0)＜l0，it can be ensured that-l0＜y x(L，t)＜l0for allt≥0.

ProofThe proof of Theorem 2 is provided in the supplementary materials.

Remark 6The energy termV1(t)is constructed based on the modeling principle of the system.To ensure that the derivative of the Lyapunov function is negative definite，a crossing termV3(t)is added.In addition，to ensure that the system satisfies the constraint，a barrier Lyapunov functionV2(t)is added.V4(t)ensures that the neural network can effectively resolve the influence of unknown disturbances.

We provide Algorithm 1 to show how the parameters are selected.

Algorithm 1 Strategies of parameter selection Input:riser stiffness E I，length of the riser L，tension T，uniform mass per unit lengthρ，and mass of the tip payload M Output:coefficientsδ1，δ2，δ3，δ4，andβ，and the control gains k1，k2，k3，and k4 1:Choose parametersαandβsuch that 0＜α＜max｛■T ρL2，■2E I ρL4｝andβ＞0 2:Choose the parametersδ1，δ2，δ3，andδ4 satisfying 0＜δ1＜αρ，0＜δ2＜ 1 αρ，0＜δ3＜T L，and 0＜δ4＜2 3:Choose parameters k1 and k4 such that k1＞0 and k4＞0 4:Choose parameter k2 based onαandδ2 according to 2(1-αLδ2)＜k2＜ δ2 T 2(1-αLδ2)5:Choose parameter k3 as k3=αM L 6:returnδ1，δ2，δ3，δ4，β，k1，k2，k3，and k4 αρL

4 Numerical simulations

In this section，numerical simulations are provided to demonstrate the effectiveness of the proposed control method for a flexible marine riser system.The steps of space and time are chosen as Δx=40 m andΔt=0.04 s.The marine riser parameters are given in Table 1.

Table 1 Parameters of the marine riser

Following Algorithm 1，we take the parameters as follows:

Suppose that the time-varying distributed disturbancef(x，t)is taken as

This riser is initially at rest and rises due to disturbances.Fig.4 shows the evolution of the riser without control.Obviously，vibrations exist due to disturbances and the riser cannot be stabilized by itself without the controller.

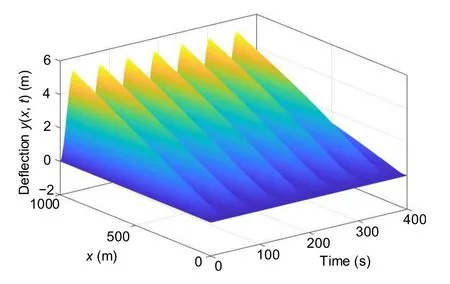
Fig.4 Evolution of the marine riser without control

The environmental disturbance is shown in Fig.5.To show the effectiveness of the proposed controller，the control input is added when the vibrations of the riser reach the maximum.Therefore，we apply the adaptive neural network based control input(17)to the riser at around 26.76 s.Fig.6 clearly shows that the system quickly reaches a stable state，and that vibrations are also suppressed immediately.Fig.7 shows the evolution ofy(L，t).It is shown thaty(L，t)tends to be stable after 100 s.Fig.8 shows the evolution ofy x(L，t)，from which it is observed that|y x(L，t)|＜0.01 is satisfied under the constraintl0.In other words，the riser is guaranteed not to exceed a certain limit during the stabilization process under controller(17).

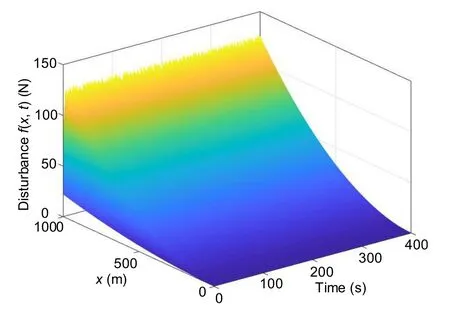
Fig.3 Ocean distributed disturbance

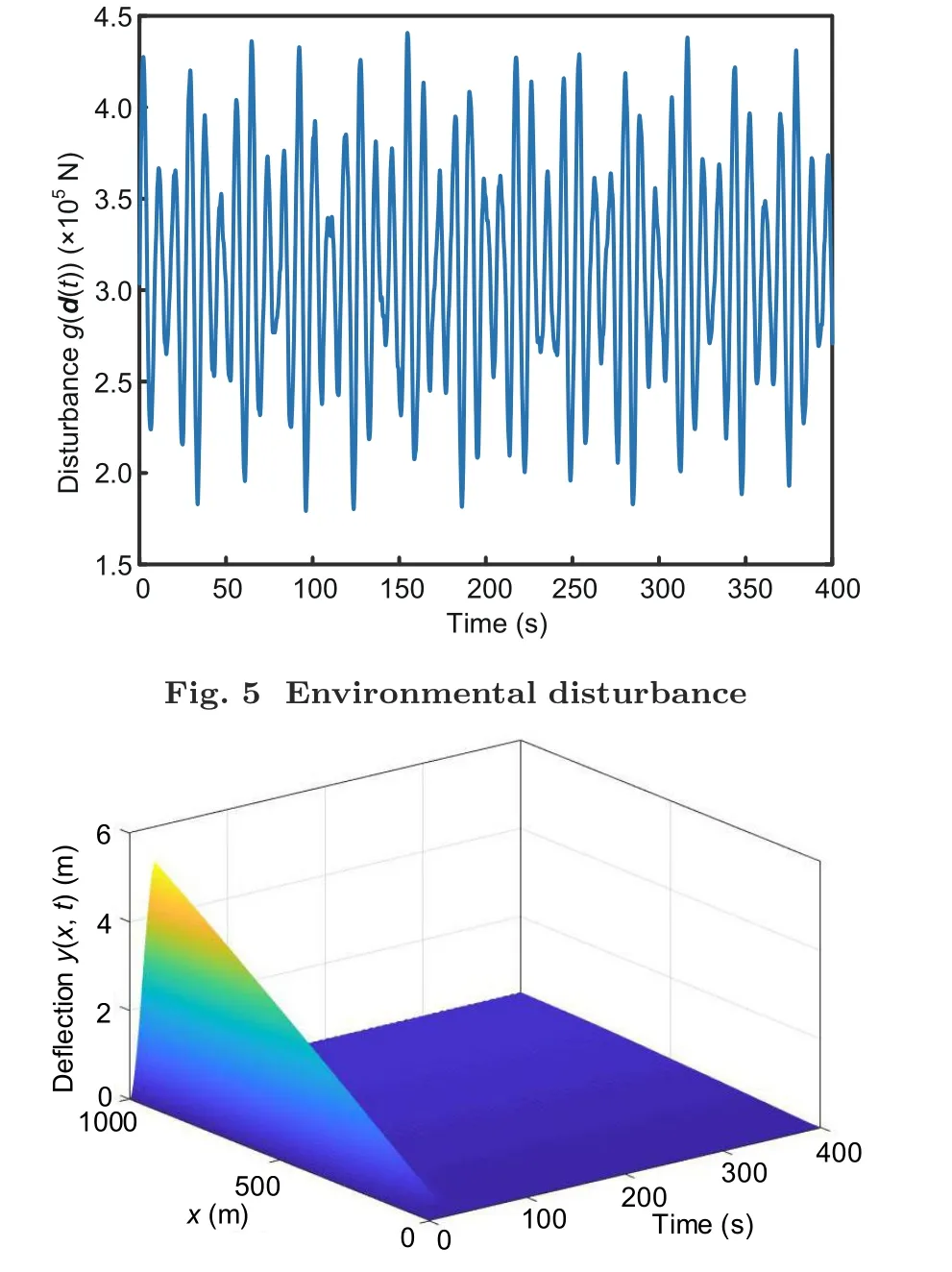
Fig.6 Evolution of the marine riser with controller(17)

Fig.7 Evolution of y(L，t)

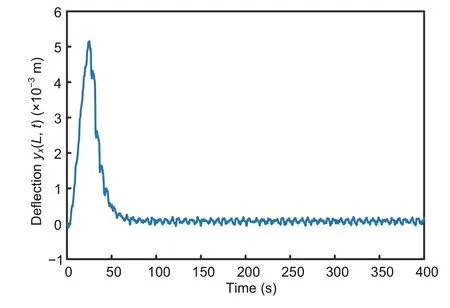
Fig.8 Evolution of y x(L，t)

To show the advantages of the proposed adaptive neural network based controller(17)，we compare it with the proportional differential(PD)controlleruPD(t)and the controlleruHE(t)in He W et al.(2011).To reduce the influence of specific controller parameters，which may affect the quality of the control effect，we perform several experiments.The best test is given here as a reference.The PD controller is

with parameters chosen as

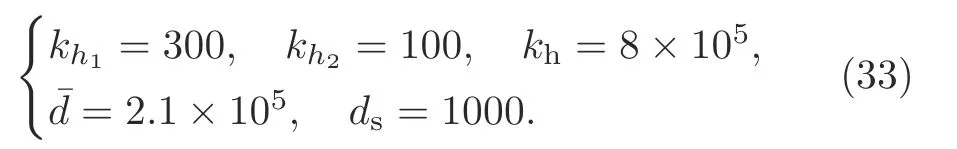
The simulation results are shown in Fig.9.Compared with our controller(17)，convergence performance of the PD controller(31)and controller(32)causes the riser position to drift from the origin.In addition，when using controller(31)or controller(32)，it is difficult to eliminate the influence of unknown environmental disturbances.It can be seen from Fig.9 that there are greater vibrations at a relatively stable state.However，the adaptive neural network based controller addresses the problem of unknown nonlinear marine riser system disturbances and adapts to the uncertainty of the system model.

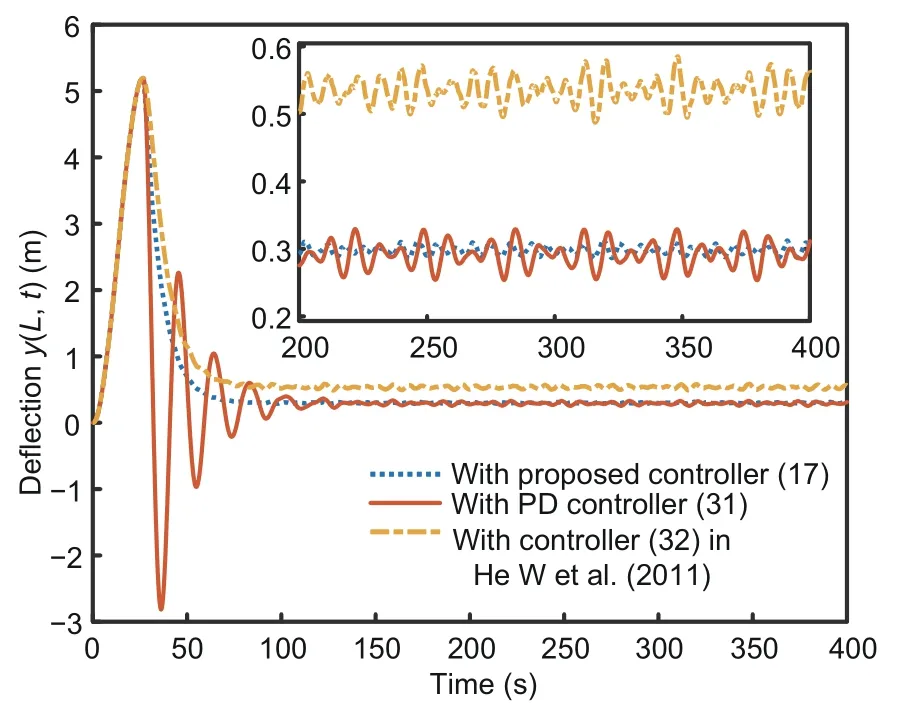
Fig.9 Comparison of the effectiveness of three controllers(control input is added at 26.76 s)

5 Conclusions

In this study，we have proposed an adaptive neural network based boundary control method to stabilize a marine riser system with output constraints.An RBFNN has been used to approximate unknown nonlinear disturbances，to represent disturbance of the nonlinear function and model uncertainty on the stability of the riser.Based on the Lyapunov function，the uniform boundness of the flexible marine riser has been proved.Finally，numerical simulations have been provided to verify the effectiveness of this proposed method.Applying the theoretical results developed in this paper to flexible systems with input saturation is one of our future topics.

Contributors

Chuyang YU and Xuyang LOU designed the research.Chuyang YU processed the data.Chuyang YU，Xuyang LOU，and Yifei MA drafted the paper.Qian YE and Jinqi ZHANG helped organize and polish the paper.Yifei MA，Qian YE，and Xuyang LOU checked the proofs.Qian YE，Chuyang YU，Xuyang LOU，and Yifei MA revised and finalized the paper.

Compliance with ethics guidelines

Chuyang YU，Xuyang LOU，Yifei MA，Qian YE，and Jinqi ZHANG declare that they have no conflict of interest.

List of supplementary materials

Proof S1 Proof of Lemma 3

Proof S2 Proof of Theorem 2