基于实车数据和BP-AdaBoost算法的电动汽车动力电池健康状态估计

周仁， 张向文，2*

(1.桂林电子科技大学电子工程与自动化学院， 桂林 541004； 2. 广西自动检测技术与仪器重点实验室， 桂林 541004)

为了应对燃油车带来的环境污染和能源危机问题，世界各国都在积极推动和发展新能源汽车，特别是纯电动汽车的研发和推广应用。纯电动车拥有零排放、零污染、成本低等优势，在中国被确定为七大战略性新兴产业之一[1]。纯电动汽车的关键技术在电池、电机、电控3个方面，而电池的能量密度远低于汽油，这严重影响了纯电动汽车的行驶速度和续航里程，而电池的老化也制约了纯电动汽车的使用寿命。另外，电池的成本在整车中占比1/3[2]。随着使用时间、充放电次数和极端工作温度影响而出现老化现象，依据IEEE Std 1188—1996标准规定，当动力电池的储能能力下降到出厂容量80%时达到报废标准，应及时更换电池[3]。因此，对电池健康状态(state of health， SOH)的准确估计，对延长动力电池的使用寿命和降低电动汽车的使用成本具有重要的现实意义和实用价值。

目前，电池SOH估计的主要方法包括实验法、模型法、数据驱动法和大数据分析法四类[4-5]。

实验法包含定义法、内阻法、电化学分析法、容量衰减法、部分放电法和阻抗谱分析法，这些方法不方便实车在线应用，在近几年中使用频率越来越低。

模型法基于寿命衰减模型、经验模型和等效电路模型，通过数学模型结合各类滤波器与估计算法来进行SOH的估计，美国阿克伦大学的Hashemi等[6]提出一种在线参数估计方法，该方法通过该参数估计器提出一种自适应滑模观测器来估计实车电池容量，可针对温度变化对电池SOH估计精度进行修正，但其温度补偿公式效果较差，实际电池SOH的估计误差在1.3%以上。

数据驱动法，国内方面，武汉理工大学的杨胜杰等[7]对电池剩余容量(state of capacity， SOC)切片分区，使用容量增量分析法 (incremental capacity analysis， ICA)提取的特征进行SOH预测，该研究选用NASA数据集中的四组电池，提取IC曲线特征基于高斯回归建立预测模型，很好地量化了SOH与IC曲线特征参数的关系，但是仅选取IC曲线的特征作为特征输入，得到的预测结果精度较低，其均方根误差(root mean squard error，RMSE)为2%；国外方面，法国巴黎-萨克雷大学的Mawonou等[8]开发了两种新的老化指标，使用充电和驾驶期间采集的数据，结合实际用户行为和环境条件，使用随机森林算法来对电池老化进度进行预测，对实车电池SOH的估计误差在1.27%左右，但这两种指标的具体提取方式并未标明，该指标与电池SOH的相关性有待考究。

大数据分析法是一种新兴方法，国内方面，北京航空航天大学的宋林军等[9]提出了基于互联网平台在线大数据的SOH估计方法，在原有数据的基础上从历史运行数据中提取的运行状况特征进行SOH预测，对不同驾驶模式下700辆电动车的监测数据集进行了测试验证，对不同类型车辆的适应性较好，但是该方法对SOH的估计误差较大，预测结果的RMSE为4.5%；国外方面，美国北达科他州立大学的Phattara等[10]使用机器学习算法基于大数据分析，采用深度神经网络方法对锂离子电池的SOH和剩余寿命进行预测，使用了NASA Ames大数据卓越中心数据库采集的实车动力电池数据集，并将结果与支持向量机、最近邻分类、人工神经网络和线性回归等算法进行比较试验，估算结果的RMSE在5%以内，该方法在保证样本适应性的同时，估计精度较低，大数据分析法精度受车辆类型影响较大，且需要体量较大的大数据平台提供数据采集服务，不利于常规性的研究，该方法发展到成熟还需要一些时间。

目前的SOH估计方法大部分都是使用实验室数据，这些数据一般在规定的温度和充放电电流下进行测试获得，具有很好的连续性和完整性。通过前面的分析可以看出，由于实际电池的循环老化寿命受到很多因素的影响[11-12]，地域温度不同、快慢充电流、非满充满放循环、数据采集丢失等原因都会造成估计的误差，因此，利用实际数据进行SOH估计的难度较大。

现利用实车数据进行SOH估计研究，通过对原始数据的清洗、筛选、填充缺失值等一系列预处理，对不同类型车辆数据进行车型分类，得到规范化的车辆数据，然后使用ICA方法提取出IC峰值与对应电压位置的特征参数，进行数据特征的相关性分析和特征选择，随后，利用稳定性高的反向传播-自适应推进(back propagation-adapt boost，BP-AdaBoost)算法进行数据训练，建立数据特征和SOH之间的联系，最后，进行SOH估计算法的验证。以期满足基于实车测试数据的SOH估计精度要求，具有一定的应用价值。

1 数据处理

1.1 数据来源

使用的数据集来源于国家大数据联盟NCBDC(National College New Energy Vehicle Big Data Application Innovation Competition)比赛的实车数据，包含京沪两地10辆在运行的车辆2018年3月—2020年3月收集的数据，时间跨度高达24个月。该数据集以《电动汽车远程服务与管理系统技术规范》(GB/T 32960—2016)为基础，大数据平台数据采样周期为10 s，得到总计1 600万行17列的数据样本。监控数据包括车辆ID、数据采集时间、车辆状态、充电状态、车辆运行模式、车速、累计里程、总电压、总电流、SOC、电池单体电压最高值、电池单体电压最低值、最高温度值、最低温度值、最高报警级别和报警标志定义数据。通过对车辆的数据特征和计算容量的分析，10辆车可以分成A、B、C、D 4个类型，为了简化分析，后续研究以C类三辆车为例，利用C类三辆车car5、car6、car9的充电数据进行研究。

1.2 预处理模型

原始数据繁多且杂乱，基于大数据处理的思维建立了一个完整的数据预处理模型，获取电池的容量和数据特征。预处理模型分为数据处理和容量处理两部分。

1.2.1 数据处理步骤

步骤1遍历数据集，根据车辆标识符把数据集分为不同车辆类型的数据集。

步骤2把每一辆车的时间数据类型由数值型转换为时间类型，方便后续操作，同时根据时间序列对车辆数据进行排序。

步骤3根据车辆状态、充放电数据、行驶里程和 SOC等相关数据，提取车辆的充电和放电片段。

预处理模型流程如图1所示。

图1 预处理模型流程图Fig.1 Flowchart of the preprocess model

1.2.2 容量处理步骤

步骤1对选用车辆数据特征进行规范化处理，根据片段内的充电电流和时间数据，区分快充和慢充行为，并使用安时积分法计算每次循环充入的容量。

步骤2将快慢充数据处理合并成同一个时间序列下的完整充电容量数据。

步骤3通过温度补偿函数对容量数据进行温度容量补偿。

步骤4通过箱型图法删除误差较大的容量结果，去除异常数据。

步骤5将首次充电数据设为出厂容量，定义此时的电池SOH为100%，后续的容量数据基于此标准转换为电池SOH特征，从而获得完整的可用容量数据集。

1.3 数据规范化

由于采集频率和使用工况等一系列不可控因素影响，实车数据准确度不高，质量较差，为了提高估计结果的精度，需要对原始数据进行规范化处理，将离散、杂乱、低质量的数据规范为便于使用的高质量数据。

数据规范化的过程如下。

(1)通过时间数据的识别对重复采样点进行合并处理。

(2)使用箱型图对超出边界的电压电流数据进行剔除。

(3)针对所属不同类型的空白值数据，选用合适的插值函数进行插值填充。

(4)删除部分缺失过大的数据。

(5)最后进行交叉验证，确认每一列的基础数据都能符合规范。

(6)将电压、电流和时间数据的单位分别统一到伏(V)、安(A)、秒(s)。

1.4 快慢充数据切分

实际车辆使用过程中存在快速充电和慢速充电的充电行为，对电池实际容量的确定存在一定的干扰[13]，不同车型受到的影响程度不同，需要单独分开处理。以C类车为例，可以通过完整充电过程的平均电流数据和总充电时间数据来划分快充和慢充，根据describe函数设定充电电流阈值为20 A、充电时间阈值为1.5 h，来综合区分car5的快慢充行为片段，结果如图2所示。

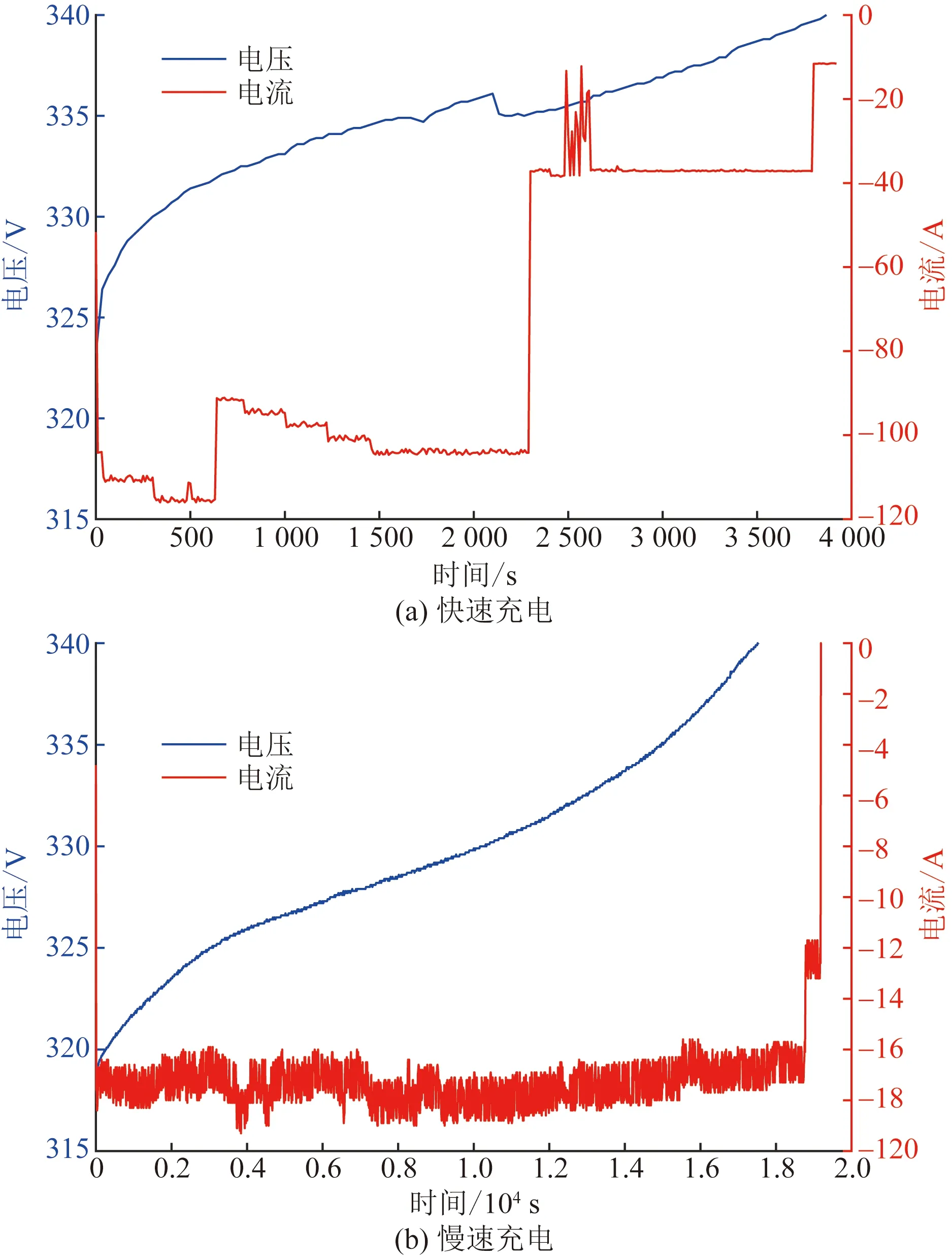
图2 两种充电行为下的电压和电流变化曲线Fig.2 Voltage and current curves under two charging behaviors

由图2可以看出，慢充过程耗费的时间是快充的4～5倍，快充过程平均电流是慢充过程平均电流的4～5倍。另外，慢充过程大部分充电电流较为稳定，不存在过大波动，可以直接使用，但是快充过程充电电流变化过大和充电过程较短，不利于平均滤波，需要对通过安时积分获取的容量结果进行进一步处理。

2 特征选取

2.1 容量标定

容量数据是一个重要的特征量，但是，原数据集没有给出，可以通过SOC数据、汽车充电行为数据和电流数据进行求解。由于实车数据都不是完整的充放电过程，放电数据由于实际运行工况的离散程度过高且连续性较差，难以清晰得到SOH相关的有效数据，而充电数据均采集于停车时的充电过程中，相对稳定，干扰因素也较少，因此，将其作为容量标定的特征数据。实际使用中，车主很少在SOC偏低时进行充电，也很少完全充电，这导致充电开始和结束时的SOC都不相同，最后根据数据量分布情况，选取在SOC位于40%～80%段的数据进行分析，该段电压电流变化相对稳定且具有代表性，用此段数据结合安时积分法得到每次循环过程中的电池容量，根据获取的电池容量，可以进行SOH的估计，计算公式为

(1)

式(1)中：Qnow-max为电池当前循环时SOC位于40%～80%的最大可用容量；Qnew-max为电池第一次循环时SOC位于40%～80%的最大可用容量。

通过安时积分得到容量数据，然后利用式(1)标定电池SOH，积分容量结果与采样时间有关，数据采集平台的采样周期存在少量差异，其中采样周期为10 s的数据占97%以上，采样周期的变化会引起容量计算的误差[13]，其中的关系如表1所示。

表1中采样周期为1 s和10 s的数据对结果的影响较低，为了确保最后得到优质、准确的SOH特征，在充电行为判断中对分段数据内间隔大于10 s的数据进行删除，保留间隔较小的数据。缺失较少的电流数据使用前后插值、平均插值、函数插值等方法进行填充，电流和时间缺失过多的充电次数仅保留时间值，容量积分结果进行剔除以免出现过大误差。

表1 采样周期与容量估计误差Table 1 Sampling period and capacity estimation error

2.2 容量处理

不同类型车辆受到快慢充行为的影响程度不同，C类车受到不同充电行为的影响最小，该类型车辆的快慢充容量结果在处理后能够统合成一个数据集，例如car5的快慢充容量结果如图3所示，随着电池循环次数增加有明显的容量下降趋势。

图3中快充容量和慢充容量变化曲线相似，容量值也属于同一量级，可以对car5的快慢充容量结果进行归一化处理，考虑到实际运行过程中快充行为和慢充行为交替进行，按照时间序列将快慢充合并为一个完整的循环老化过程。

除了充电电流的影响之外，数据时间跨度高达两年，实际运行环境的温差较大，考虑到电池温度对容量造成的影响，对初步计算得到的容量结果进行温度容量补偿操作。根据实车数据，结合文献[11]相同特征的经验公式，经过数据拟合得出合适的对数函数模型为

K=-0.068 3lgT+0.790 9

(2)

QT=QK

(3)

式中：T为某次循环电池组的平均温度， ℃；K为温度补偿系数；Q为安时积分法得到的容量；QT为温度修正后的容量。两个常数-0.068 3、0.790 9通过实验测试结果进行拟合得到。

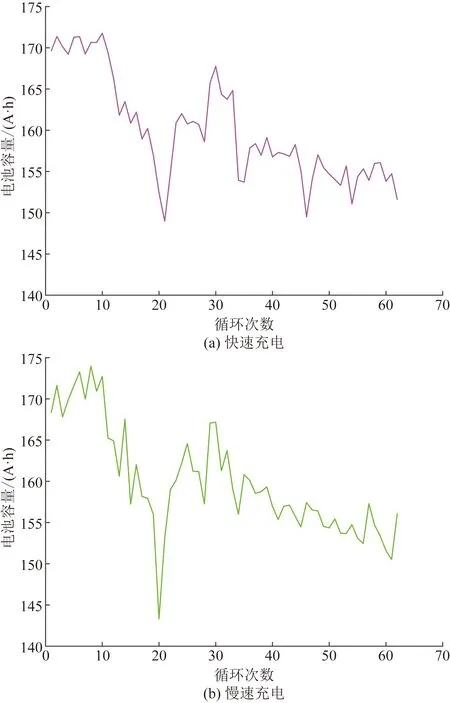
图3 car5的快慢充容量结果Fig.3 Fast and slow charging capacity results of car5

数据集中没有单体温度高于40 ℃或者低于0 ℃的数据，所以不考虑过高温度带来的容量下降因素。通过单体最高温度和最低温度计算得到平均温度数据，作为温度补偿函数的修改依据。基于式(2)和式(3)，可以得到温度修正后的结果如图4所示。

由图4可以看出，相对于温度修正之前的快慢统合结果，经过温度修正后的结果波动更小。安时积分法得到的容量结果在40次循环时存在异常，主要原因是car5在40次循环时最低温度为0 ℃，导致实际充入电池的电量过少，反之，较高环境温度时则会充入比平时更多的容量。对此类数据进行温度补偿后，电池容量数据均方差有所降低，比仅仅使用安时积分法得到的容量数据更加符合容量衰退规律，在一定程度上修正了温度变化所带来的误差。

图4 添加温度补偿后的容量对比Fig.4 Capacity comparison after adding temperature compensation

2.3 特征选取与相关性分析

动力电池的充放电过程是非常复杂的电化学变化过程，测试数据的特征与电池SOH之间具有较高的关联性，其中IC曲线的峰值点与电池的反应速率和储能能力有关[14-15]。ICA方法不仅适用于车载动力电池的低倍率充电过程，也同样适用于高倍率充电过程[16]，选取车辆的快充和慢充数据不会造成ICA结果出现误差，且选取的车辆数据都是在恒流充电情况下采集的，所以可以通过分析充电过程中的IC曲线峰值高度与对应电压关系得到与电池SOH相关的特征。以car5的数据为例，基于ICA方法，每间隔20次循环提取一次循环的IC曲线，并且通过高斯滤波器对噪声进行平滑处理，该处理目的是为了找到明显的IC峰值点，然后根据该峰值点选取原数据坐标，并不会影响数据的真实性，最终得到容量增量峰值与对应电压位置变化的关系曲线如图5所示。

由图5可以看出，容量增量峰值随循环次数增加而有所降低，峰值对应电压位置随循环次数增加在一定程度上右偏。第80次循环峰值不明显，出现平台区的原因是部分慢充过程时间较长，电压变化缓慢，而第100次循环峰值存在左偏异常，是由于快充过程充电电流的波动较大导致的。

新提取的特征需要进行关联度分析[15]，通过皮尔森相关系数法对该特征参数与SOH进行相关性分析，car5的峰值和对应电压位置数据与电池SOH的关联度分别为0.895 8和0.813 4，因此，这两个特征都可以作为模型估计的特征参数。

除了上述的ICA特征之外，为了降低实车数据中部分合理的强噪声对单一特征预测结果稳定性的影响，同时也为了提高模型估计精度，选取了实车数据充电过程中的一段充电数据的容量样本作为特征样本输入，综合数据分布的可视化分析和真实充电行为的特征分析，最终选定每次充电循环中SOC在50%～60%段的累计充入容量作为容量样本，该段充电过程中容量、电压和电流数据变化趋势最为平缓，且片段长度较短不会导致过拟合现象。由于其本身就是与SOH计算相关的一部分数据，所以不需要进行相关性分析。

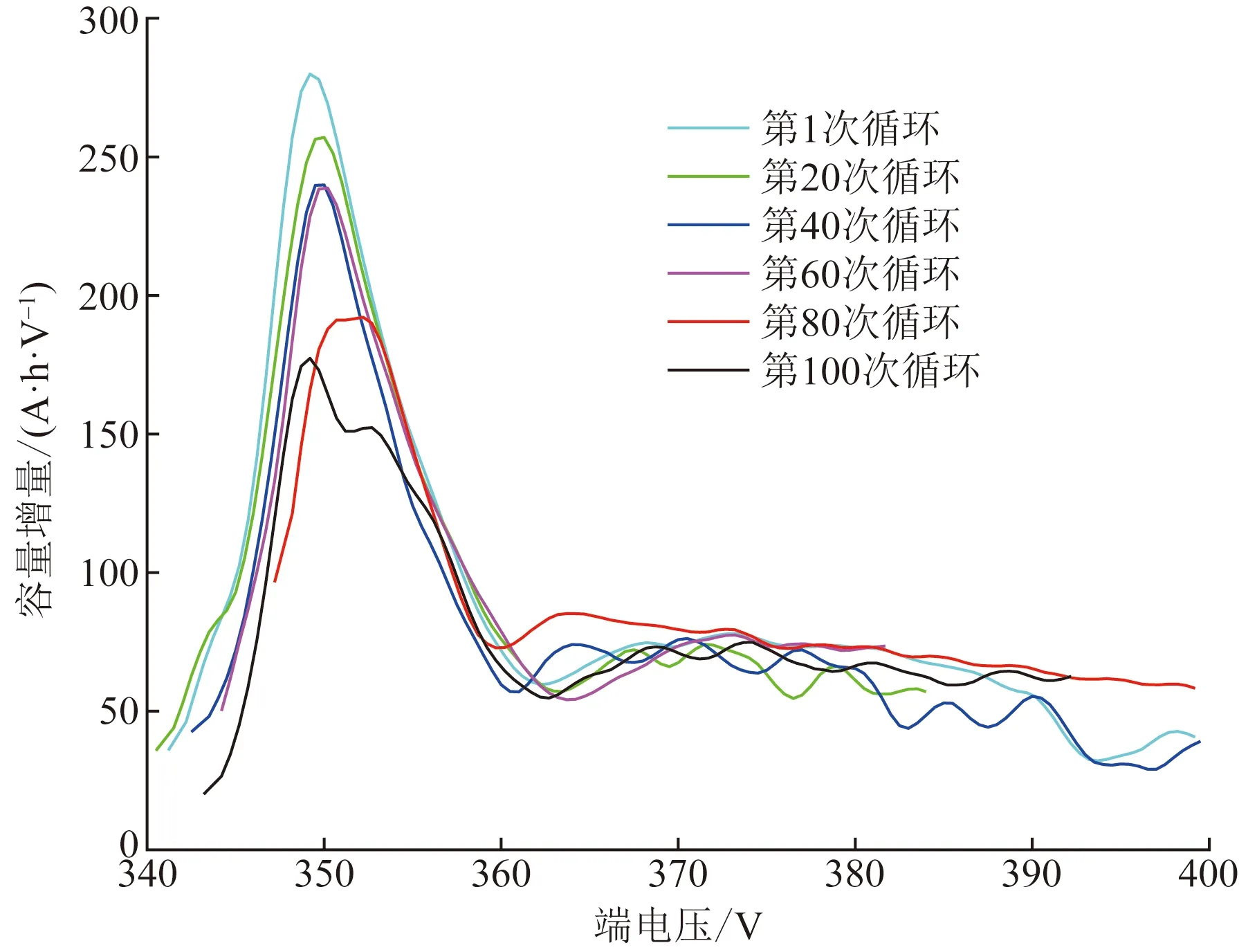
图5 电池IC曲线Fig.5 IC curve of battery

3 预测模型

3.1 算法选择

长短期记忆-循环神经网络(long short term memory-recurrent neural network，LSTM-RNN)模型广泛地用于数据预测研究，其结构为多个LSTM单元构成的RNN模型，可以有效地捕捉连续性数据在时间维度上的长期和短期特征依赖，电池老化过程属于时间序列问题，该类问题使用LSTM-RNN模型的效果较好[17]，但这种算法的鲁棒性较差，多次预测结果之间均存在1%～3%的不一致预测结果。

在使用实车运行数据集进行数据处理时，对影响SOH结果且占此次循环数据总量不超过5%真实数据都予以保留，视为可用数据，反之视其与SOH的相关性进行处理或直接剔除。故而部分循环数据在实际数据集中并不是连续的，且实际运行数据的工况较为复杂且数据量巨大，出现部分状态正常但数据结果离群值较大的正常数据，该类数据存在有隐含特征，让依赖记忆前期数据特征的LSTM-RNN模型的预测结果受到较大的影响。后通过对该类数据结果的微观分析发现，实车数据存在日常使用下的隔夜不满充满放行为以及不规律用电带来的电池长时间静置等问题，导致前后两次充放电循环过程的数据时间性关系较差，数据特征在时序性上出现跳跃性的波动，所以预测结果在出现较多的离群点数据后，LSTM-RNN算法的预测结果往往会连续出现一系列误差。

针对这一问题，选择了与实车数据问题类似的股票价格预测问题中较为新颖的AdaBoost算法，对实车数据结果进行预测，最终结果表明，该算法可以较好地处理不规律数据变化问题[18]。使用BP-AdaBoost算法通过叠加法以AdaBoost算法为框架，以反向传播(back propagation，BP)算法为弱预测器，优化样本节点和弱预测器的权重，最终得到强预测模型。BP-AdaBoost算法可以利用n个BP网络组成的弱预测器，最快速地挖掘数据特征，然后通过优化提升权重分配将多个弱预测器的输出结果合并输出，最大程度降低数据噪声对学习效果的影响，提升估计效果。同时对输入特征要求也不高，不需要额外进行特征筛选，强预测器可以弥补弱预测器由于误差积累所带来的缺陷，因此，将BP-AdaBoost算法应用于基于实车数据的电池SOH估计研究。

3.2 算法设计

BP神经网络是一种常用的神经网络，其原理是通过数据信号的正向传播与误差的反向传播来学习数据集内在关联特征。BP神经网络结构简单，仅由输入层、隐藏层和输出层组成，解决回归问题具有准确率高和训练速度快的优点，适合用于构建AdaBoost算法中的弱预测器。负反馈过程中该网络对每一个样本输出的结果y，都会通过式(4)计算其与预期结果Y的误差率Er，即

Er=(Yr-yr)2

(4)

式(4)中：r为输入网络的第r个样本。对所有样本的均方误差进行求和，得到BP神经网络的目标函数，为了得到最优的结果，只需要最小化式(5)中的误差函数Ek，即

(5)

式(5)中：M为样本总量。BP网络中局部数据的误差不会对全局结果造成很大影响，适用于消除真实数据中强噪声对后续预测结果的影响，也是选择该神经网络构造AdaBoost模型弱预测器的原因。结构上通过使用AdaBoost算法规则组合n个BP网络为强预测器，有效改善了 BP 神经网络自身容易过拟合停留在局部最优的情况，提高了整个模型全局搜索能力。为了提高模型预测精度，最终模型的输入样本包括容量样本和ICA特征样本，这两种特征在迭代过程中的权重采用分开分配的策略，其实现过程如图6所示。具体步骤如下。

步骤1导入容量样本集和特征样本集，对其简单规范化预处理后，输入由BP神经网络构成的弱预测器，利用car5数据集中124次充电循环数据来训练模型，每一个初始训练样本点最开始的权重W1=1/124，在此样本权重下得到x1，通过x1训练得到一个基本预测器H1，设置一个期望的误差区间，根据H1对样本的预测结果与真实值y进行比对，判断预测结果是否在误差区间内，从而对样本进行分类并进行权重更新。预测失败的样本数据，提高数据样本权重，使其更贴近真实值，已经预测成功的样本数据，则降低权重，不对其分类结果进行修改。

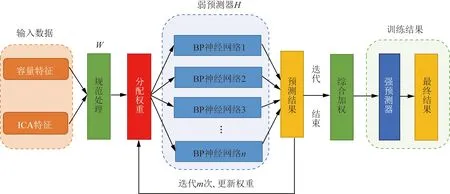
图6 BP-AdaBoost算法流程图Fig.6 Flowchart of the BP-AdaBoost algorithm

步骤2根据新的权重分布训练弱预测器Hn，将数据迭代m次，每次迭代中都进行样本权重更新。同时将每一次BP网络的预测结果与真实容量进行对比，根据样本预测结果对样本权重进行更新，样本权重更新公式为

(6)

(7)

式中：Wmn为第m次迭代第n个预测器输入的样本权重；Hn为表示第n个预测器；Zm为标准化因子；an为弱预测器的权重；n为预测器的数量；y为电池SOH的真实值。

步骤3计算BP网络预测结果与真实容量的误差率E，作为最终弱预测器权重更新的依据，完成m次迭代后，将所有的弱预测器结果综合加权得到强预测器模型，该算法能够修正一部分实车容量数据问题带来的偏差，提高模型收敛速度，稳定预测结果，比较适合实车电池SOH的估计模型，弱预测器Hn的权重更新公式为

(8)

式(8)中：En为第n个预测器的误差率。

首先，BP-AdaBoost模型根据样本点的预测结果进行样本权重的迭代修改；其次，根据每次BP网络的误差率给所有的BP网络分配权重；最后，得到基于BP神经网络融合AdaBoost算法的电池SOH强预测器模型。

3.3 预测结果

为了验证设计算法的有效性，建立了BP-AdaBoost模型，利用同一类型3车辆的car5、car6和car9的实车数据进行训练、验证和测试，数据量比例约为2∶1∶1。为了防止循环次数长度干扰模型预测，car9数据量最大作为训练集，car6作为验证集，用于在预测过程中对参数进行寻优辅助模型建立，car5作为最后的测试数据。作为对比，同时建立了LSTM-RNN模型，利用相同的训练数据和测试数据进行验证。

利用car5的数据进行测试的结果如图7所示，可以看到LSTM-RNN模型前20次循环预测结果误差较大，全过程中的预测值普遍高于真实值，且对于波动较大的实车数据，无法很好地对其进行预测，特别是在电池SOH下降速度较快的98%～94%部分。这是由于LSTM-RNN中的梯度优化过程受到数据噪声影响，并且实车数据的循环时间不是等距序列，间隔增大时LSTM会失去学习信息的能力，导致误差增大，从而影响模型估计精度。

图7 两种方法估计结果Fig.7 Prediction results of two methods

BP-AdaBoost模型在数据开始阶段，估计误差同样较大，预测结果出现稍许滞后现象，通过样本权重的再分配，有效地消除了波动较大数据对结果的影响，能够很好地贴近实车数据结果，随着弱预测器权重的迭代修正能够很好地提高模型稳定性，多次预测结果相差极小，且随着迭代次数增加，效果进一步提高。

两种算法模型在电池老化循环刚开始时的估计误差均保持在较低范围，但是LSTM-RNN模型在电池SOH出现较大变化后，对实车电池SOH的估计精度明显降低，而BP-AdaBoost模型的估计精度能在出现波动后迅速平复，相比之下误差更低。为了更清楚地显示两种方法的估计结果变化，绘制两种算法的估计误差曲线如图8所示。

图8中，LSTM-RNN模型受到真实数据骤降影响，在第50次循环之后误差普遍较大，表明该模型的抗噪声能力较差。BP-AdaBoost模型总体效果较好，稳定性强，大部分预测结果均方根误差在0.9%以下，虽然受到第90次循环真实值骤降的影响，后续预测结果出现波动，但能通过权值修改在一定程度上降低部分突变数据的影响。因此，BP-AdaBoost模型对于实车数据噪声的抗干扰能力较强，稳定性较好，能够对电池SOH进行准确的预测。为了更全面地比较两种算法的估计结果，分别计算了RMSE、平均绝对误差(mean absolute error，MAE)、平均绝对百分比误差(mean absolute percent error，MAPE)，结果如表2所示。

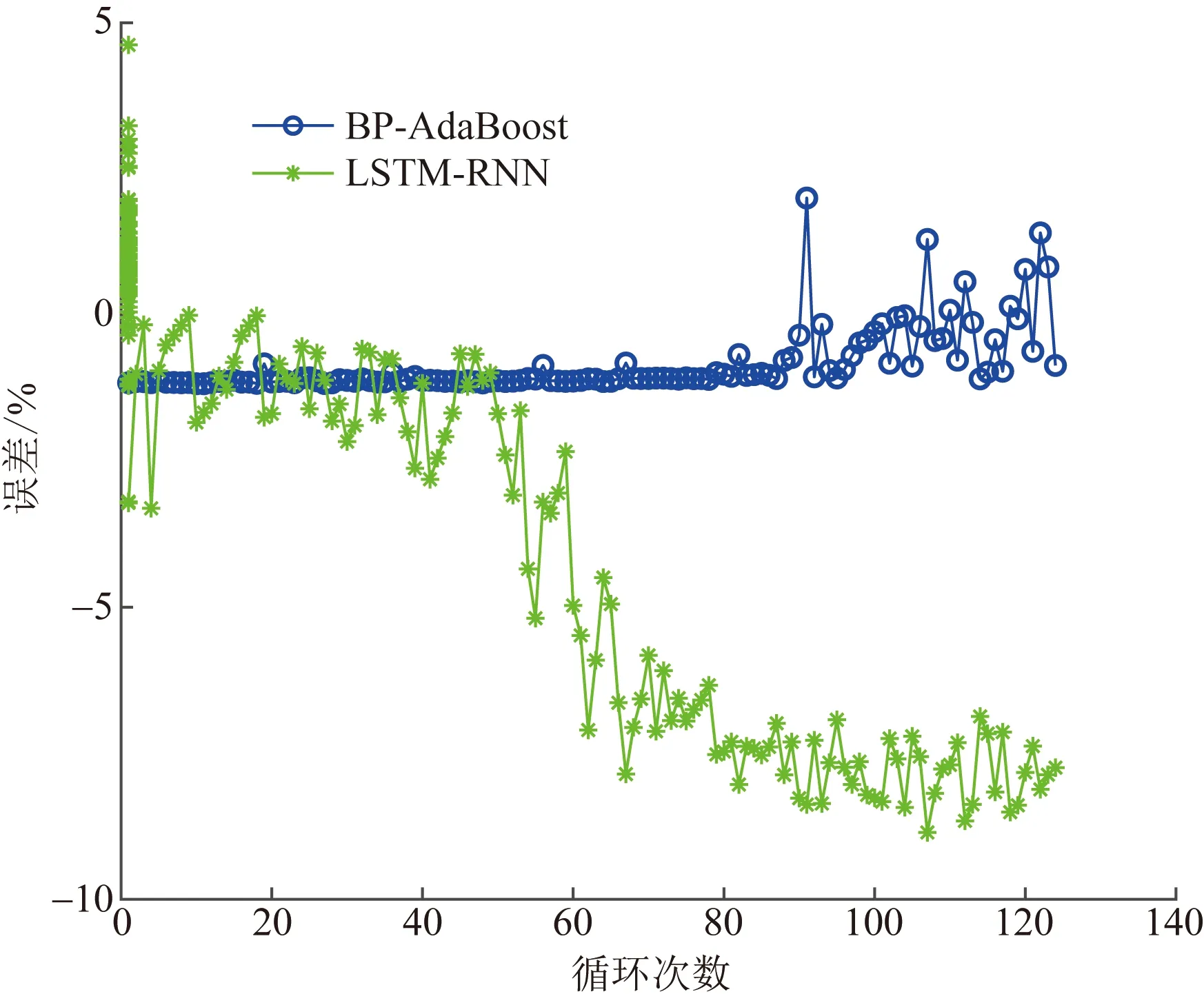
图8 两种方法结果误差Fig.8 The result error of the two methods

表2 两种方法评价指标对比Table 2 Comparison of evaluation indexes of two methods

由表2可以看出，相比于LSTM-RNN模型，BP-AdaBoost模型的3种评价指标较低，BP-AdaBoost模型的均方根误差为1.116%，相比于LSTM-RNN模型降低了4.4%，其平均绝对误差表现最好，误差精度达到了0.963%，相比于LSTM-RNN模型降低了3.629%，而平均绝对百分比误差为1.009%，相比于LSTM-RNN模型降低了3.664%。综合3种评价指标，BP-AdaBoost模型在实车数据的电池SOH估计上效果更好、精度更高。

4 结论

基于实车数据对电动汽车动力电池SOH估计算法展开研究，结论如下。

(1)使用大数据分析的处理方法，对京沪两地实际运行的电动汽车数据进行数据预处理，得到符合模型估计精度的动力电池容量数据，在此基础上进行温度容量补偿和汽车快慢充电的容量修正，降低了数据分布的离散性，最终在保证数据真实性的情况下，得到了新的可用于模型预测的实车运行数据集。

(2)同时使用容量特征和数据特征作为测试样本输入，容量特征使用了电池SOC在50%～60%段累计充入的容量，数据特征则通过ICA方法寻找电池IC曲线峰值和对应电压位置参数得到，并验证了该特征参数与SOH之间具有高关联度，可适用于实车数据预测。

(3)针对实车数据部分不可处理的强噪声和时序性差的问题，使用BP-AdaBoost算法进行SOH的估计，BP-AdaBoost模型对同一类车型表现出良好的适应性，预测结果更加贴近真实值，表现最好的MAE评价指标达到0.96%，可以满足实际工况下的电动汽车动力电池SOH估计精度要求。