基于轨迹数据的信号交叉口排队长度估计

王志建， 金晨辉， 龙顺忠， 郭健

(北方工业大学城市道路交通智能控制技术北京市重点实验室， 北京 100144)

交通信号灯被设计用来从时间上分离相互冲突的交通流，确保交叉口的交通安全。通行权的转换会导致进口道的排队过程产生周期性变化，然而，随时间变化的交通需求和不当的信号配时往往容易导致交叉口排队长度和延误的增加，进而出现一些极端的拥堵现象比如排队溢出和网络锁死[1-3]。一种准确、稳健的排队长度估计方法对于信号交叉口的性能评价和信号控制优化具有重要意义。此外，通过队列长度可以估计其他性能指标，例如延误、停车次数、行程时间和燃油消耗和污染物排放，这些指标对于评估节点运行状况和改善节点服务水平有着显著的积极作用。因此，许多先前的研究学者都致力于开发准确可靠的信号交叉口排队长度估计模型。现有的队列估计方法主要可分为两大类，一类是基于设施型检测器的排队长度估算，另外一类是基于移动全球定位系统(global positioning system，GPS)数据的排队长度估算。

基于设施型检测器的排队长度估算方法对检测器布设的位置、数量以及场景有着严格的要求。此外，考虑设施型检测器的全生命周期，其过高的出厂成本以及维修费用，使得“全城全覆盖”难以实现。随着车辆定位和检测技术(例如探测车辆系统和车载汽车导航系统)的发展，使用浮动数据估计队列长度已经受到国内外学者的广泛关注[4]。与设施型检测器相比，基于移动GPS数据成本低且覆盖范围广，能够更精准地获取车辆的实时位置信息，但是无法获得所有车辆的信息，只能获得采集到的部分数据，这种不确定性是利用移动GPS数据的最大挑战[5-7]。此外，现有方法主要关注信号交叉口的平均排队长度或排队长度的长期分布。很少有研究涉及实时队列长度估计的问题，信号交叉口实时排队长度估计这有助于许多重要的应用，如动态信号控制策略和实时交通状态获取[8-9]。随着智能移动技术的最新发展，使大量实时高频率的探测车辆轨迹数据的获取成为现实，这些数据越来越多地被用于城市道路网络交通问题研究。因此，基于探测车轨迹数据的队列长度估计因其固有的优势而受到越来越多的关注[10]。

以前的研究为信号交叉口排队长度的估计提供了很好的方法。然而，以前关于采样间隔和渗透率的研究大多基于信号配时和到达模式信息是已知的，这些严格假设一定程度上限制了这些方法的实用性。此外，先前的研究是对一个周期的全部浮动车轨迹数据进行分析，并估计最终的排队长度。这种方法虽然充分利用了轨迹数据，但是因为会因为无法剔除波动较大的数据造成较大的误差。

针对上述文献中提及的排队长度估计方法的局限性，现不假设车辆特定的到达模式和特定的渗透率，通过单独使用轨迹数据来估计信号交叉口的队列长度，提出一种基于浮动车集群队列的排队长度估计模型，通过一系列模拟实验来验证所提出的方法可以产生比基准估计方法更精确和稳定的估计，尤其在稀疏数据场景下，研究的优势将更加突出。相关的研究成果将为交叉口的交通状态评估以及信号配时优化提供数据支撑。

1 最大排队长度估计原理

在图1中，红色线段ab代表交叉口的红灯相位，bd段代表交叉口的绿灯相位，在一个理想的排队过程中，车辆到达较为均匀，驾驶员行为也较为单一，此时探测车的轨迹如图1(a)所示，其中当交叉口红灯亮起时，停止线前的车辆将陆续制动停车，这一排队集结的过程可视为由红灯相位发出的集结波(ae段)，其波速记为v。当相位由红变绿时，停止线前的车辆将陆续启动，这一排队消散的过程可视为由绿灯相位发出的消散波(be段)，其波速记为w。当集结波与消散波相遇时(e点)该周期内的排队长度达到最大值，最大排队长度为e点到停止线的距离，即ec段的长度。而在实际的排队过程中，由于实际的车辆到达并不均匀，司机的驾驶模型不同，集结波的波速不是一成不变的，排队波将表现为波速不同的多段折线，如图1(b)中ae段，波速记为Va、Vb、Vc、Vd。

当拥有某交叉口浮动车数据集时，可以通过动力学公式对特定的采样点计算得到浮动车停止点，如图2中的蓝色点表示浮动车轨迹的GPS采集点，红色点如S1和S2为通过采集点计算得到的停止点。将集结波分段进行拟合，并通过波速判别约束，识别出最后一段集结波。

同样也可以通过计算浮动车的启动点，如图3的蓝色点表示浮动车轨迹的GPS采集点，红色点D1、D2、D3为通过采集点计算得到的启动点，再通过启动点拟合出排队的消散波。

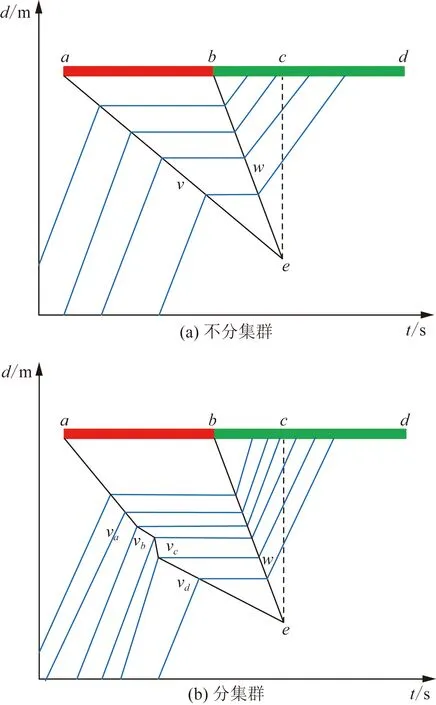
图1 一个信号周期内排队集结过程和排队消散过程图解Fig.1 Illustration of the queuing build-up process and queuing dissipating process in a signal period

建立的模型创新点在于提出当集结波最后一段与消散波的交点即是该周期内达到最大排队长度的点，区别以往研究中对周期内所有的点进行拟合，造成较大的误差，如图4中波速为vn的集结波与波速为w的消散波的交点e，其在时间轴上的投影为达到最大排队长度的时间，排队的最大长度为ce线段的长度。

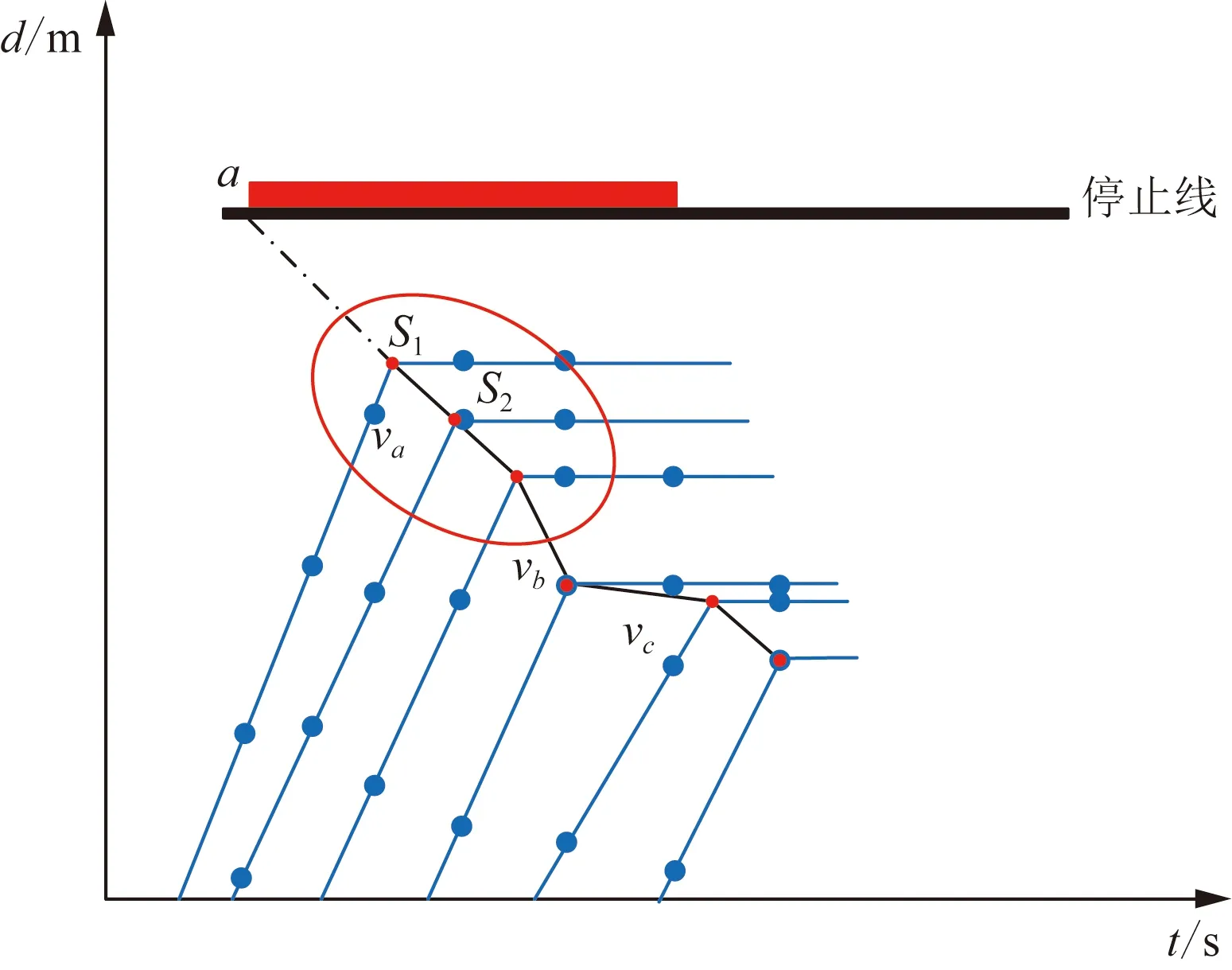
图2 通过加入排队点估计集结波Fig.2 The aggregation wave is estimated by adding queuing points

图3 通过离开排队点估计消散波Fig.3 Estimation of dissipated waves by leaving the queue points

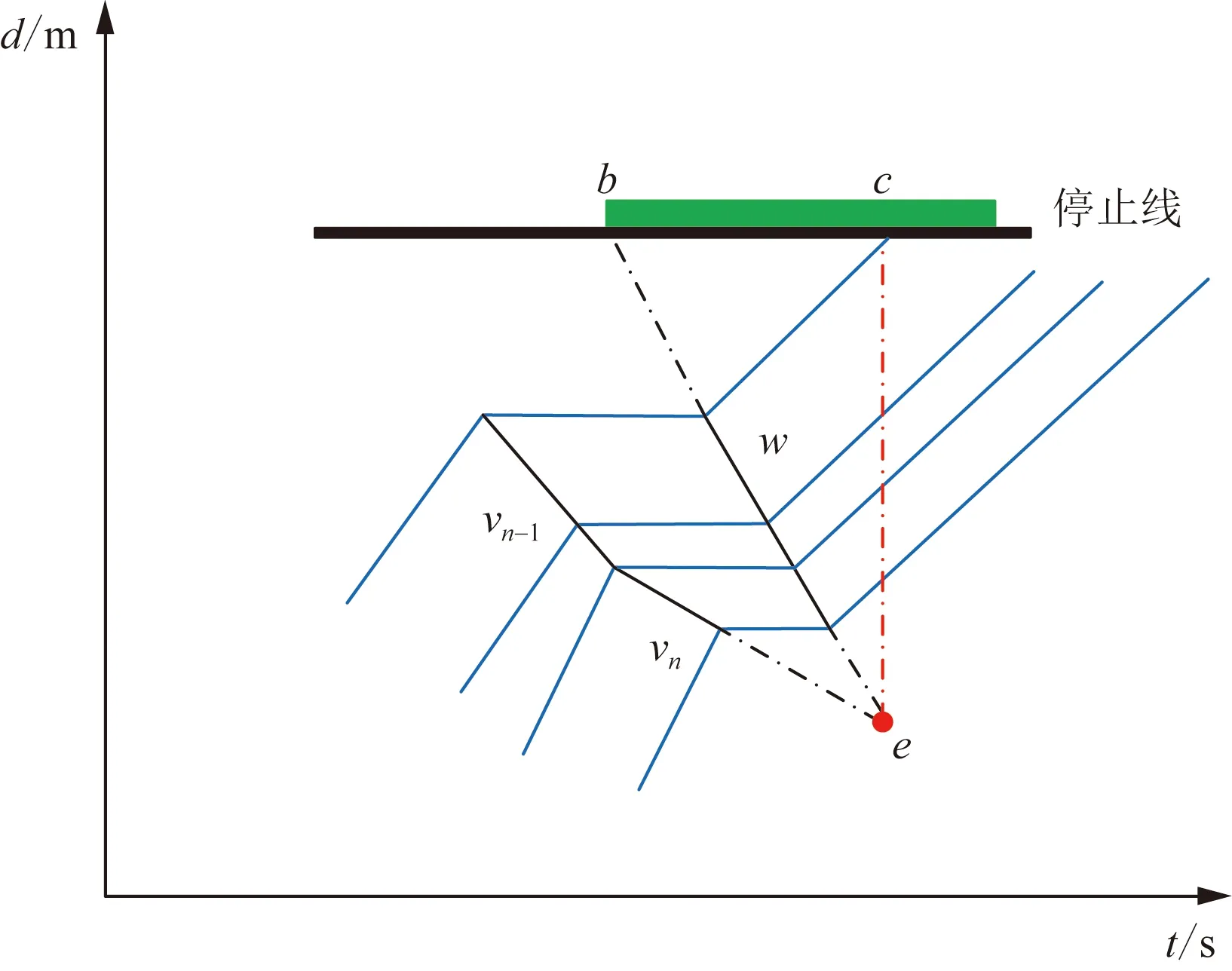
图4 利用集结波和消散波估计排队长度Fig.4 Estimation of queue length using build-up wave and evanescent wave

2 基于轨迹数据的队列集散模型

2.1 排队过程识别

假设所有驾驶员都是有经验且遵守交通法规的，在观察到交通信号灯相位即将由绿变红或发现前方有排队车辆时就会控制车速，使车辆进入缓行状态，直到最终减速到速度为0。

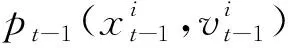
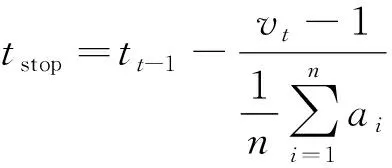
(1)

对于一个周期内的所有停止点，按照时间顺序排序为集合{S1，S2，…Sn-1，Sn}，首先取集合Slast为{Sn-1，Sn}，对Slast用最小二乘法表示为

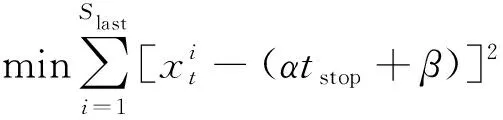
(2)

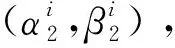
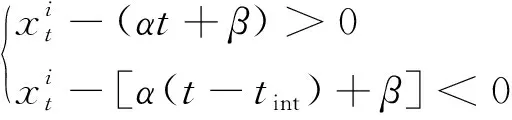
(3)

式(3)中：tint为轨迹数据的采样间隔。

对集合Slast添加点Sn-2，同样通过最小二乘法可表示为

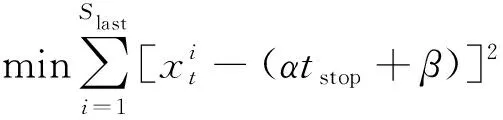
(4)

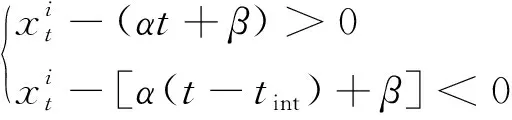
(5)

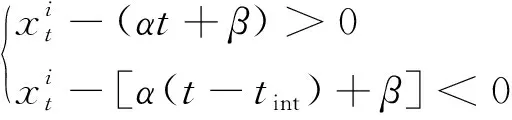
(6)

2.2 消散过程识别

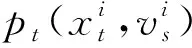
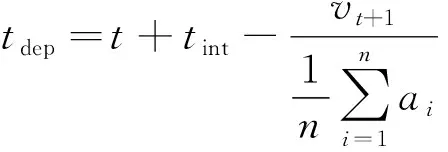
(7)

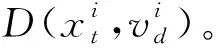
对同一周期内的所有启动点D，通过最小二乘法可表示为

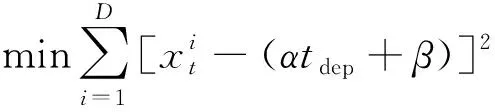
(8)

计算得到(α，β)，其中(α，β)需满足的约束条件为

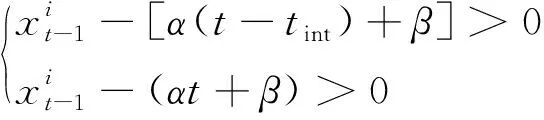
(9)

3 排队长度估计

根据图1中利用波函数估计最大排队长度的原理，结合上一小节波函数的求解公式，对一个浮动车数据集D，D中共包含n个周期，记这些周期为T1，T2，…，Tn。在周期Tn内如果有足够的点能得到集结波函[最后一段的系数(αlast，βlast)和消散波的系数(αdep，βdep)，那么可以通过求解方程组得

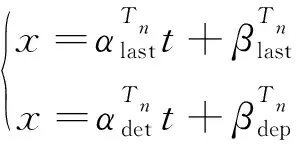
(10)

得到(x，t)，该点即为Tn周期内的排队长度达到最长时的点位。

4 模型验证

4.1 排队长度估计模型验证

首先对研究的路口——青羊区人民中路一段和羊市街交叉口进行实地调研，调研内容包含路口的渠化情况、信号控制方案等，并对研究的西进口道的早高峰(8:00—9:00)、晚高峰(18:00—19:00)、平峰(11:00—12:00)的流量进行了统计，实地调研的数据作为SUMO仿真的输入，为了更好地表明模型在全时段的适应性，最后研究3个时段在不同的渗透率和时间间隔下模型的稳定性和普适性。模型仿真示意图如图5所示，流量输入数据如表1所示。

利用西进口道的浮动车轨迹进行模型验证，路口信号控制为二相位东西方向相位：红灯60 s，绿灯40 s，信号周期为100 s，分别采用时间间隔为2、4、6、8、10 s和渗透率为5%、10%、15%的浮动车轨迹数据集，对建立的周期长度估计模型进行验证，排队车辆在交叉口前由于信号灯的作用会经历集结和消散两个过程，由于车辆到达具有随机性，车辆往往以车队的形式集结，首先对轨迹数据进行筛选，识别具有排队行为的数据集，通过集结过程和消散过程的进入排队点和离开排队点分别进行拟合计算出波函数，再根据波函数计算排队长度。

以早高峰流量进行仿真，采用浮动车5%渗透率，采样间隔为4 s的仿真的数据集为例，分别用考虑集群车队的模型和不考虑集群车队的模型对每个周期内最大排队长度进行估计，得到实际的排队长度和预测的排队长度如图6所示。

在共70个周期中，由于数据采样的随机性，且模型对单周期的浮动车数有最小值约束(一个周期至少两辆)，最终识别出了66个有效周期。为了验证本文模型的精度，以不分车队集群的模型作为比较对象，分别预测以上66个有效周期的最大排队长度，并计算平均绝对误差(mean absolute error，MAE)，公式为

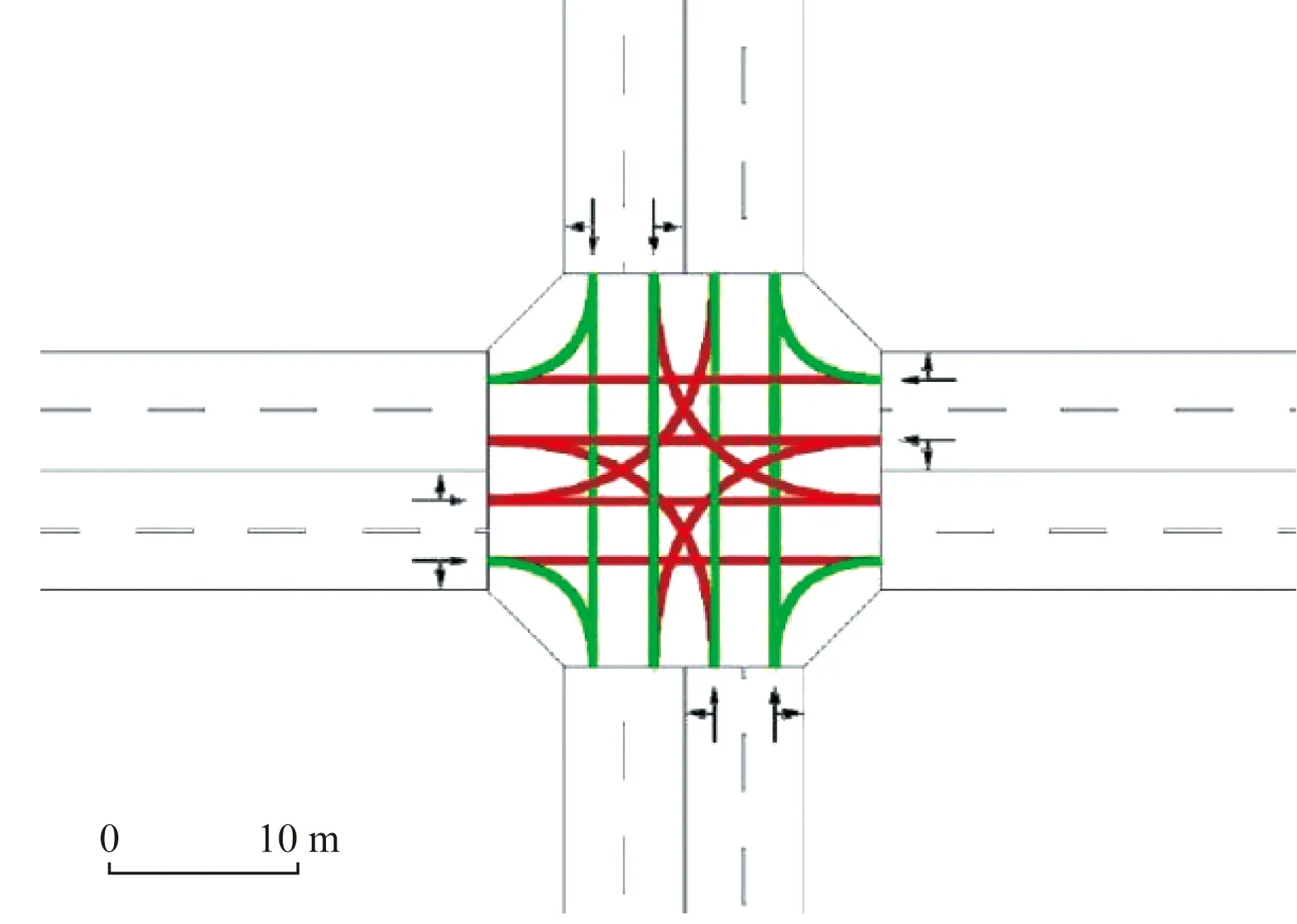
图5 青羊区人民中路一段和羊市街交叉口仿真示意图Fig.5 Map of the intersection of Renmin Middle Road and Yangshi Street in Qingyang District

表1 车流量输入Table 1 Traffic input

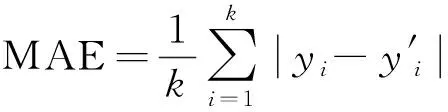
(11)

计算可得不分集群车队平均绝对误差为10.08 m，分集群平均绝对误差为7.87 m，精度提高约20%。计算结果表明，本文模型与部分集群的模型相比在预测精度方面有显著优势。

以晚高峰流量进行仿真，采用浮动车5%渗透率，采样间隔为4 s的数据集为例，分别用考虑集群车队的模型和不考虑集群车队的模型对每个周期内最大排队长度进行估计，得到实际的排队长度和预测的排队长度如图7所示。

在共70个周期中，最终识别出63个有效周期。显然，与早高峰流量相比有效周期数减少了，这是十分合理的，随着流量的降低，一些周期的浮动车数量减少，由于数据采样的随机性和模型对单周期浮动车数的最小值约束导致有效周期数减少。同样地，分别使用分车队集群和不分车队集群的模型对有最大排队长度预测值的周期计算其平均绝对误差(MAE)，分集群绝对误差9.56 m，不分集群车队绝对误差19.99 m。

图6 早高峰流量输入下实际值和估计值对比Fig.6 Comparison of actual and estimated values under high-level flow input

图7 晚高峰流量输入下实际值和估计值对比Fig.7 Comparison of actual and estimated values under medium-level flow input

以平峰流量进行仿真，采用浮动车5%渗透率，采样间隔为4 s的数据集为例，分别用考虑集群车队的模型和不考虑集群车队的模型对每个周期内最大排队长度进行预测，得到实际的排队长度和预测的排队长度如图8所示。

在共70个周期中，最终对56个周期的最大排队长度进行了预测，有14个周期少于等于1辆。分别使用分车队集群和不分车队集群的模型对有最大排队长度预测值的周期计算其平均绝对误差(MAE)，分集群平均绝对误差为19.72 m，不分集群车队平均绝对误差为24.62 m。

由上述分析结果可知，本文模型在早高峰流量下更能体现出它的优越性，早高峰流量下本文模型相比于不分集群的模型更能精准的估计每个周期的排队长度，误差较小，随着流量的减少，在晚高峰流量下模型的精度也有所降低，当流量减小到一定程度，即每个周期能获得的浮动车轨迹逐渐减少，在平峰流量下模型的精度和相比其他模型的优越性都有所降低。

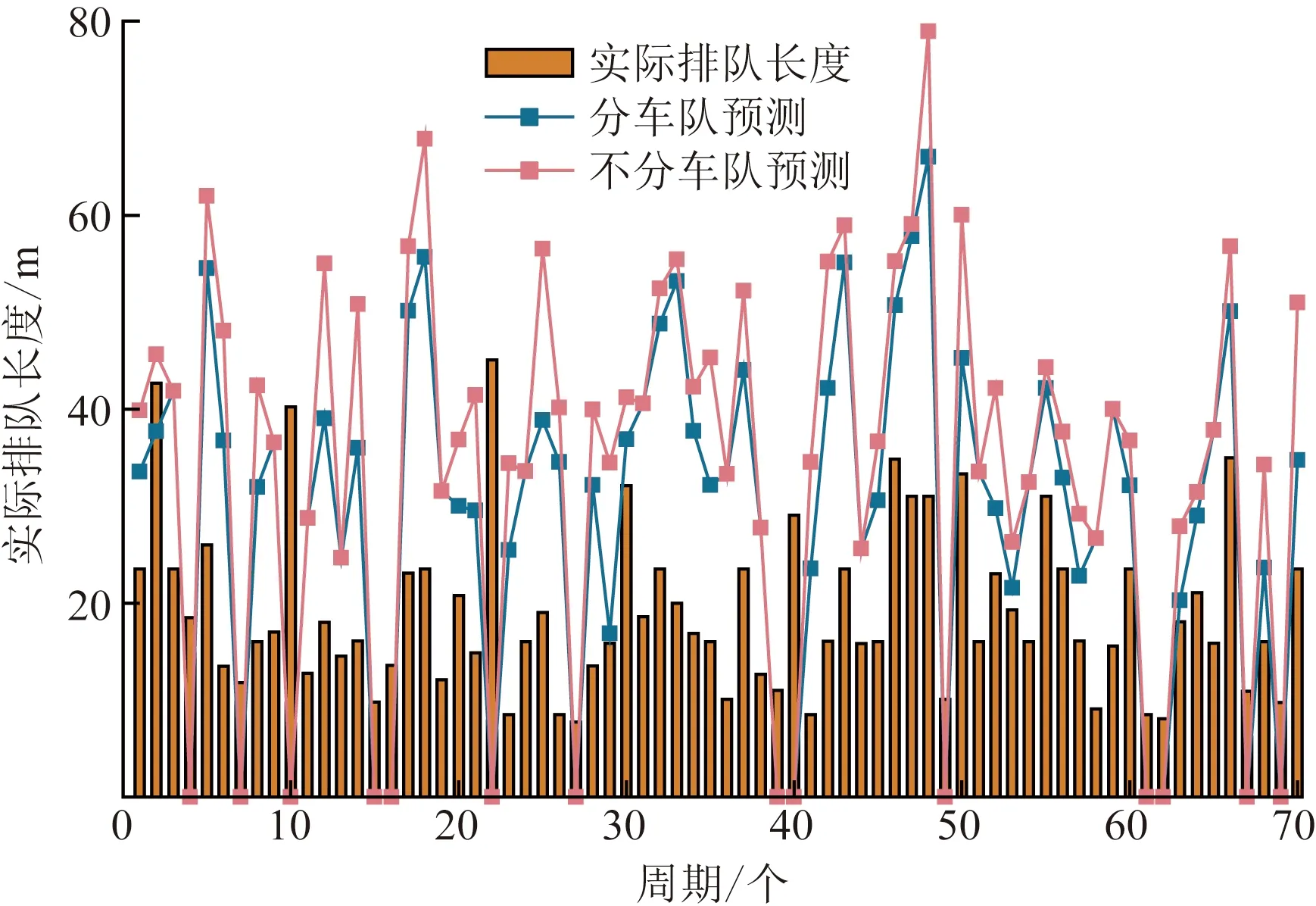
图8 平峰流量输入下实际值和估计值对比Fig.8 Comparison of actual and estimated values under low-level flow input

4.2 与其他模型的效果对比

为了研究本文模型与不分集群队列的模型在不同的渗透率和不同的数据采集间隔下的效果，对早高峰流量、晚高峰流量、平峰流量影响下分别采用时间间隔为2、4、6、8、10 s和渗透率为5%、10%、15%的数据集代入模型估计排队长度，进行对比。平均绝对误差(MAE)越小越好。

使用平均绝对误差作为评价预测结果的标准，早高峰流量影响下不同的采样间隔与不同的浮动车渗透率下对分集群模型与不分集群模型预测排队长度的平均绝对误差对比如表2所示。

同理，晚高峰流量影响下不同的采样间隔与不同的浮动车渗透率下对分集群模型与不分集群模型预测排队长度的平均绝对误差对比如表3所示。

同理，平峰流量影响下不同的采样间隔与不同的浮动车渗透率下对分集群模型与不分集群模型预测排队长度的平均绝对误差对比如表4所示。

通过对早高峰流量、晚高峰流量、平峰流量影响下分别采用时间间隔为2、4、6、8、10 s和渗透率为5%、10%、15%的数据集代入模型进行多组对比实验，结果表明，样本采样间隔越小，渗透率越高时，模型预测精度越高。在早高峰流量下和晚高峰流量下，本文模型的预测精度与不分集群模型相比误差更低，而在平峰流量下，两个模型的性能相差不大，这是由于在流量较少时采集的有效样本量较少，如果只有两辆浮动车的轨迹，那么分集群和不分集群的结果是一样的，此时，不分集群模型就是分集群模型的特例。但是此时用本文模型估计的平均绝对误差也仅仅为19.58 m，在实际的一些应用中，20 m以内的误差仍有很大的应用价值。

5 结论

通过分析轨迹数据，并对车辆进入交叉口前运动状态进行了合理的假设，取得的研究成果如下。

(1)首先建立了集结波和消散波估计模型，然后建立了排队长度估计的集群队列模型，最后使用浮动车轨迹数据验证模型并与相关方法进行了多组对比试验。

(2)在模型验证中，为了更好地表明模型在全时段的适应性，首先将采用早高峰、晚高峰、平峰的流量作为SUMO仿真输入，对早高峰流量、晚高峰流量、平峰流量3种等级流量影响下分别采用时间间隔为2、4、6、8、10 s和渗透率为5%、10%、15%的数据集代入模型进行多组对比实验。实验结果表明本文模型在不同的流量等级下适用性都较强，误差在可接受的范围内，随着流量等级的提高，本文模型表现出较好的优越性。即使在平峰流量，低渗透率下，本文模型估计的排队长度误差仍然可以达到理想效果。

表2 早高峰流量输入下与不分集群预测排队长度的平均绝对误差对比Table 2 Comparison of the average absolute error of the predicted queue length under high-level traffic input and the non-cluster prediction queue length

表3 晚高峰流量输入下与不分集群预测排队长度的平均绝对误差对比Table 3 Comparison of the average absolute error of the predicted queue length under the medium-level traffic input and the non-cluster prediction

表4 平峰流量输入下与不分集群预测排队长度的平均绝对误差对比Table 4 Comparison of the average absolute error of the predicted queue length under low-level traffic input and the non-cluster prediction queue length