基于系统动力学-云模型的抗浮锚杆系统风险等级评价

乔建刚， 王傑， 李景文

(河北工业大学土木与交通学院， 天津 300401)

地下空间资源不断开发，抗浮工程的破坏失效使大量地下结构物的变形、开裂甚至整体破坏，抗浮工程安全性愈来愈受到重视[1]。因此合理准确地评价抗浮锚杆系统风险等级对促进地下结构安全运行十分重要。国内外学者对于抗浮锚杆在地下结构中的受力特性[2]、拉拔特征[3]和破坏机理[4]进行深入研究，但对于抗浮锚杆系统整体所处于风险情况的评价以及对风险等级的界定鲜有研究，抗浮锚杆系统风险等级评价指标体系仍不够完善。

在评价方法方面，针对系统风险评价的理论方法较多，如刘祥康等[5]采用改进层次分析法对含硫气井屏障系统失效风险，Jiskani等[6]利用z值改进模糊理论对露天矿井系统运营风险进行分析和评价，Maghrabie等[7]综合灰色系统理论，对多准则决策评价方法进行了提升，Wang等[8]利用模糊集对逼近理想解排序法(technique for order preference by similarity to an ideal solution，TOPSIS)模型进行改进，来解决多属性决策问题。上述方法对抗浮锚杆系统风险评价做出了贡献，但抗浮锚杆系统风险的影响因素具有模糊性，使得常规的模糊数学和统计学方法失去意义[9]，评价过程中无法兼顾指标之间相互影响作用与风险等级的不确定性。

云模型理论可有效处理定量信息与定性信息之间相互变换存在的模糊性，多用于安全评价中[10]。如高磊等[11]用驱动力-状态-响应(drive-state-response，DSR)-云模型评价高地温隧道施工安全。因此为构建一套完善抗浮锚杆系统风险等级评价体系并解决其风险等级评价过程中存在的复杂性和模糊性，在应用系统动力学分析抗浮锚杆系统锚固界面力学失效机理的基础上，现构建风险等级评价体系，结合云模型提出风险等级评价方法，以期为抗浮锚杆系统风险预防、安全保障提供准确可靠的决策支持。

1 抗浮锚杆系统风险等级评价指标体系构建

1.1 锚固界面风险形成路径

抗浮锚杆锚固界面是否失效是抗浮锚杆系统能否实现抗浮功能的关键，掌握其锚固界面子系统风险形成路径可以采取相应措施控制系统风险。

1.1.1 锚固界面力学失效机理

地下水浮力作用在抗浮锚杆上的拉拔载荷转化为锚固界面上的应变能，随着地下水浮力对抗浮锚杆系统的持续作用，应变能不断地得到积聚，进入应变能传递阶段。在应变能传递过程中，会经历弹性阶段、弹塑性阶段、塑性阶段以及完全脱黏阶段共4次的能量控制机制，直到锚固界面完全脱黏为止[12]。因此，应变能是导致锚固界面子系统变形与破坏的根本原因，锚固界面的破坏失效是一种不正常的能量释放。

根据热力学第一定律，能量之间的平衡关系为

U=Ud+Ue

(1)

式(1)中：U为锚固界面上的应变能，即锚固界面上的应变能；Ue为锚固界面可释放弹性应变能；Ud为锚固界面单元耗散能。

如图1所示为锚固界面弹性应变能与耗散能之间的关系示意图。

锚固界面受到的外界拉拔载荷作用能全部转化为输入总能量U，即图1中应力-应变σ-ε曲线下方的总面积。图中阴影部分的面积为弹性应变能Ue，锚固界面子系统的弹性变形为可逆过程，卸载后弹性应变能可以全部释放。σ1为加载过程中的应力值，ε1为与应力所对应的应变值，应力-应变曲线下方白色部分的面积为耗散能Ud，用于锚固界面内部微裂纹的生成，并最终形成宏观主裂纹而导致锚固界面发生失稳破坏，其中耗散能Ud为U-Ue。

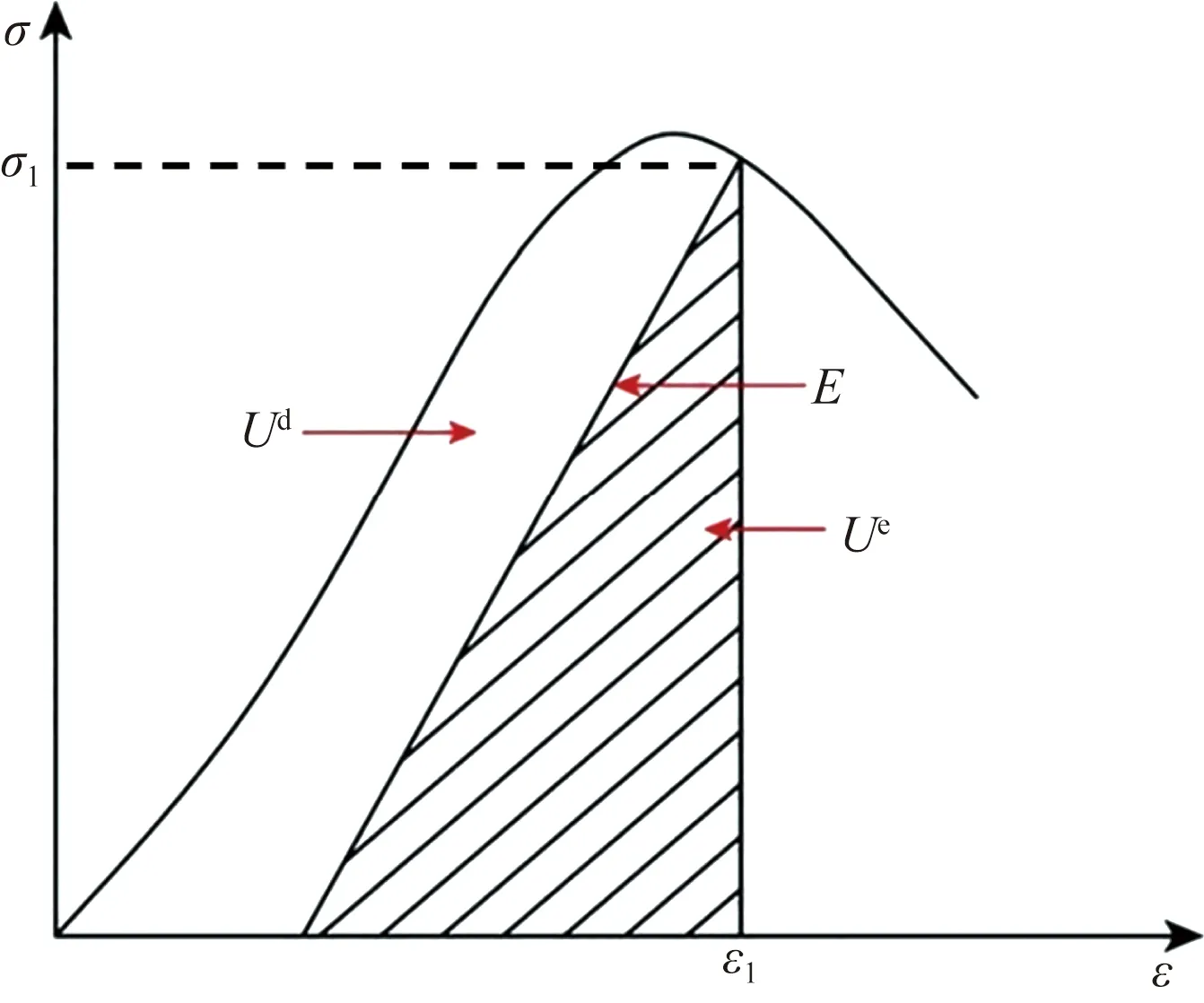
图1 锚固界面弹性应变能与耗散能之间的关系Fig.1 Relationship between elastic strain energy and dissipated energy at anchorage interface

锚固界面输入总能量U与锚固界面弹性应变能Ue为

(2)

(3)

1.1.2 锚固界面子系统风险形成路径系统动力学分析

利用Vensim软件对上述锚固界面子系统失效机理进行因果分析，如图2所示。

锚固界面子系统风险的主要影响包括物的影响(如岩土体的物理力学性质、地下水渗流情况等)和人为影响(如锚杆支护类型、设计参数、施工质量等)[13-15]，结合锚固界面子系统的因果分析图绘制系统动力学流图，从能量的角度找出锚固界面失稳的状态变量，如图3所示。

由图3可知，系数CD、JD、DT分别表示应变能传递速率、应变能耗散速率和应变能输入速率的影响系数，取决于风险影响因素综合情况。外界地下水浮力扰动会持续向锚固界面子系统传递能量，一部分应变能会按照耗散速率进行耗散，另一部分应变能会使子系统内的应变能持续增加，因此导致锚固界面子系统失效破坏的状态变量即为系统内存储的应变能，当系统内应变能积聚到一定程度时，应变能会以可释放弹性能的形式直接释放，导致锚固界面子系统破坏失效。

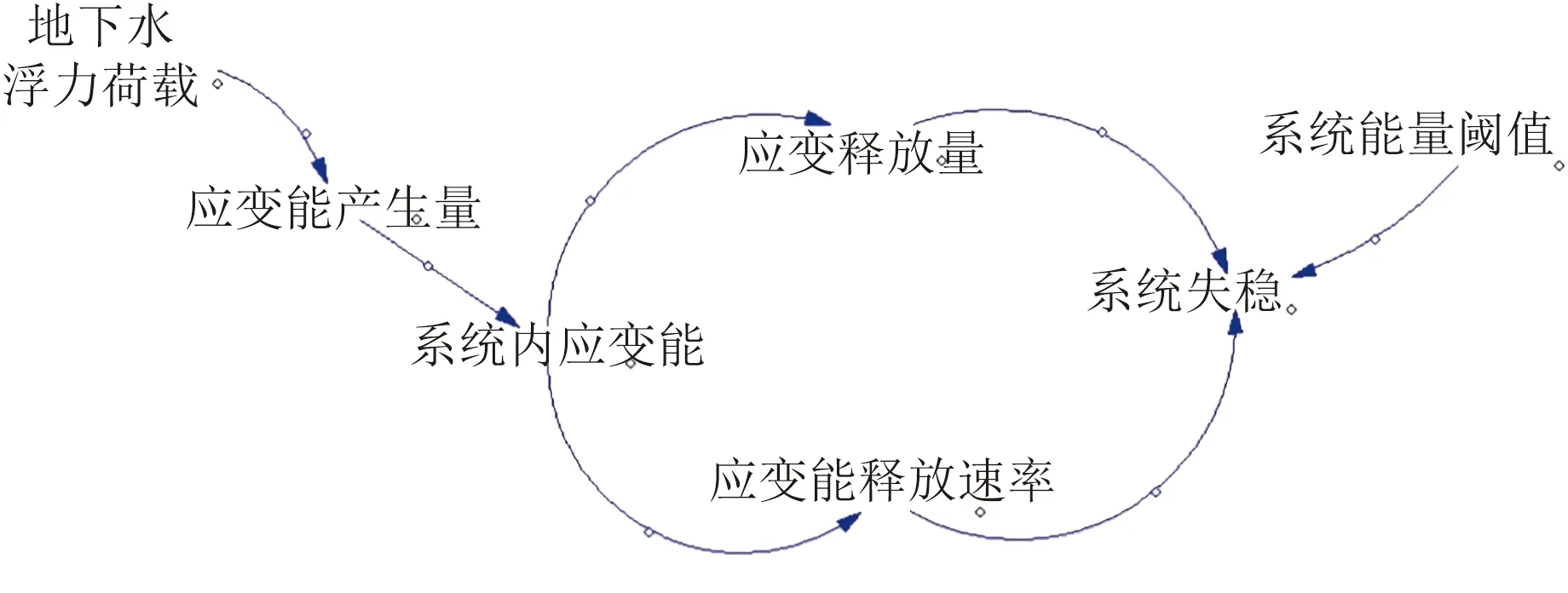
图2 锚固界面子系统能量因果分析图Fig.2 Energy causality analysis diagram of anchorage interface subsystem

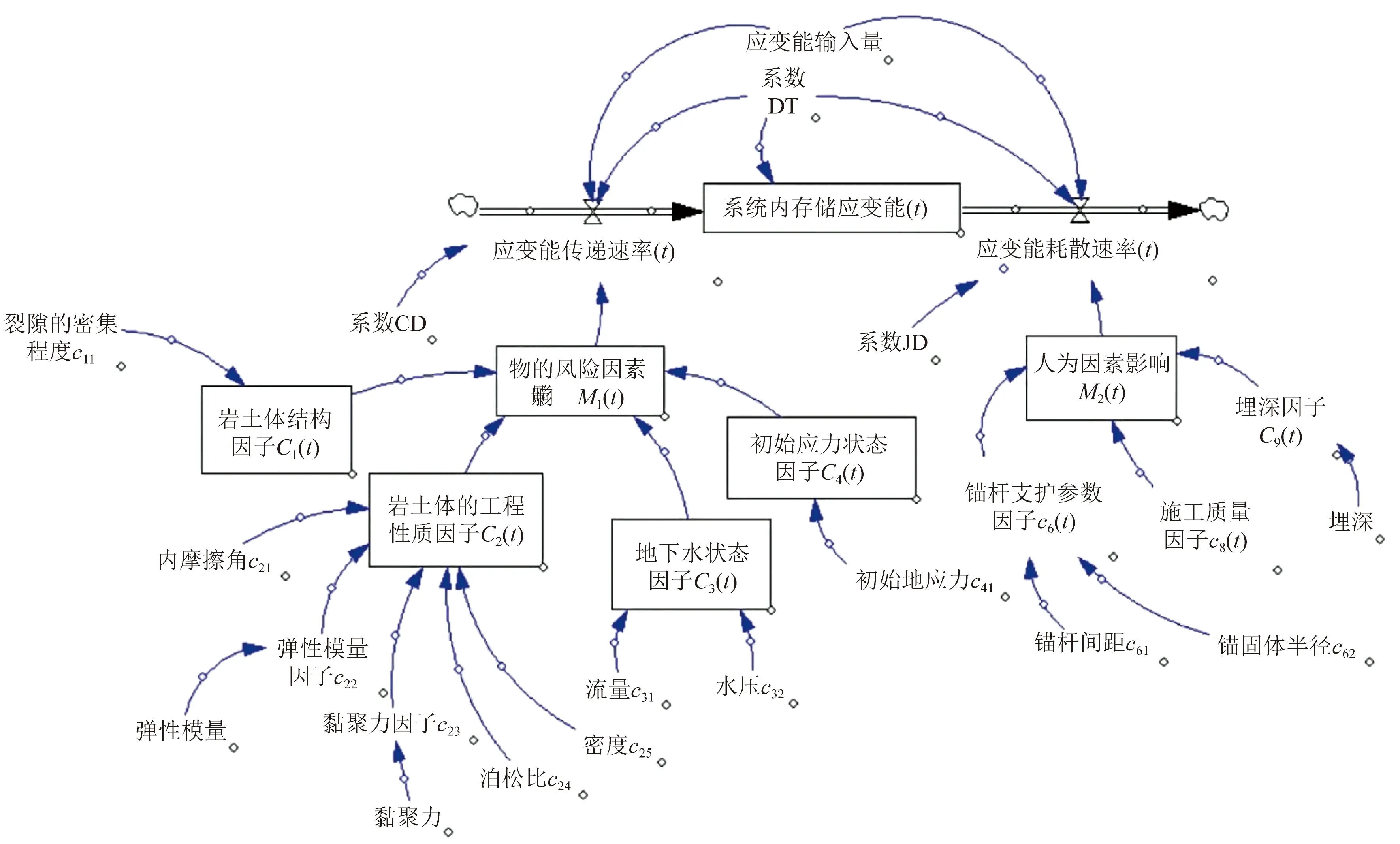
图3 锚固界面子系统系统动力学流图Fig.3 System dynamic flow diagram of anchorage interface subsyste

在整个应变能传递、释放过程中，应变能传递速率主要由抗浮锚杆系统周围物的风险因素决定。风险因素影响由岩土体结构因子、岩土体的工程性质因子、地下水状态因子、初始应力状态因子等因素所决定。其中，岩土体结构因子主要由裂隙的聚集程度决定，岩土体的工程性质主要由内摩擦角、弹性模量、黏聚力、泊松比及密度等因素决定，地下水状态主要有地下水流量和水压决定，初始应力状态主要由初始地应力决定。应变能耗散速率主要由人的风险因素决定。人的风险因素影响由锚杆支护参数因子、施工质量及埋深等因素所决定。其中埋深因子由地下结构埋深所决定，锚杆支护参数因子由锚杆间距、锚固体半径决定。

1.2 评价指标体系构建

根据锚固界面子系统系统动力学流图分析出的风险形成路径，结合规范《地铁及地下工程建设风险管理指南》[16]和研究文献[17-18]，考虑对抗浮锚杆系统工程实施过程中有较大影响的风险因素，最终选取4个一级评价指标和14个二级评价指标，构建抗浮锚杆系统风险等级评价指标体系，如表1所示。

结合专家意见，抗浮锚杆系统风险等级评价指标体系各指标的风险等级统一分为5个评价等级，即S={[Ⅰ，“可忽略的”]， [Ⅱ，“需考虑的”]， [Ⅲ，“严重的”]， [Ⅳ，“严重的”]， [Ⅴ，“严重的”]}，对应标度区间为[0，2]、[2，4]、[4，6]、[6，8]、[8，10]。

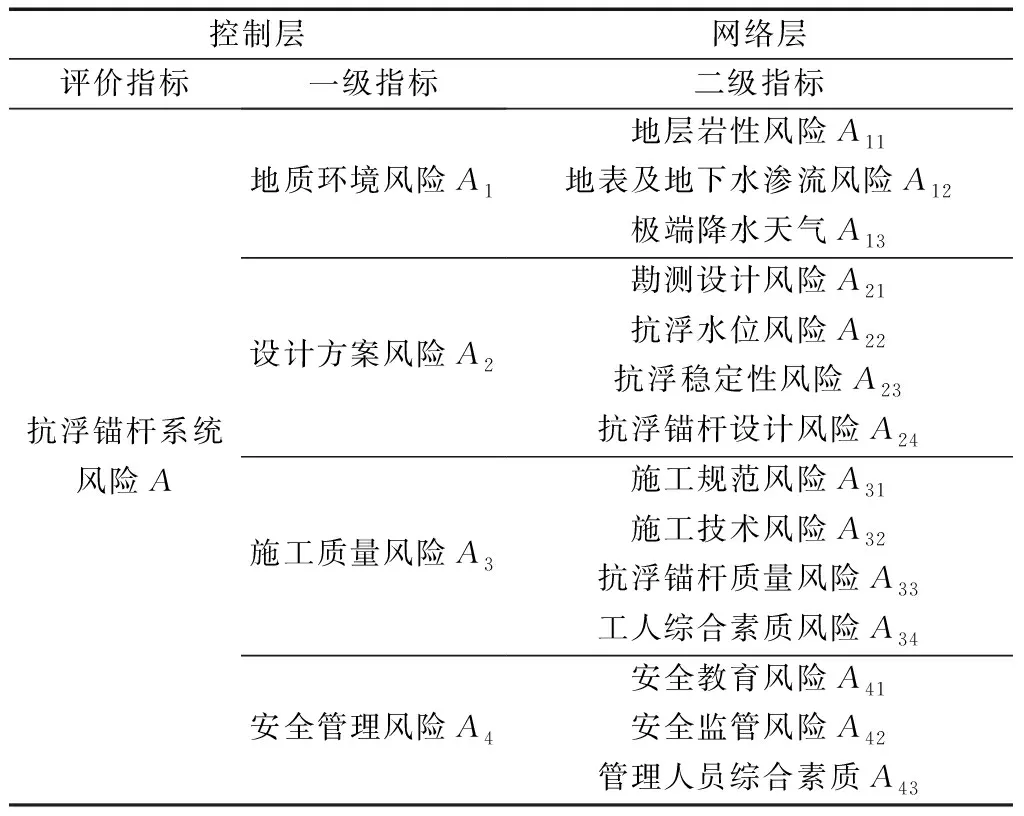
表1 抗浮锚杆系统风险等级评价指标体系Table 1 Risk grade evaluation index system of anti-floating anchor system

2 基于ANP-熵权法的指标权重确定

在确定抗浮锚杆风险等级评价指标体系后，需要对各个指标进行合理赋权使评价结果更加真实准确。选取主观赋权法中的网络层次法(analytic network process， ANP)法[19]和客观赋权法中的熵权法确定主客观权重并进行组合优化。设ANP法得到的主观权重为w(i)=(w1，w2，…，wn)，熵权法得到客观权重ω(i)=(ω1，ω2，…，ωn)，利用博弈论中的纳什均衡[20]求解综合权重Wij，该手段可以对两种方法的妥协和一致进行集成，既能综合两种方法优点，也能进一步减少专家打分的不完全准确性以及熵权法脱离实际的机械性。综合权重Wi为

Wi=a1w(i)+a2ω(i)

(4)

式(4)中：a1、a2为主观、客观权重的组合系数；以两者利益最大为目的。将Wi和w(i)、ω(i)的离差极小化为目标，优化组合系数，目标函数为

(5)

3 抗浮锚杆系统风险等级评价方法

3.1 云模型

构建抗浮锚杆系统风险等级评价指标体系并且指标权重确定后，需专家根据实际抗浮锚杆系统工程，在自身知识和经验的基础上对系统所面临风险等级做出评价，评价结果不可避免具有复杂性和模糊性。云模型由李德毅等[21]基于模糊和概率论提出，使用特定算法替代模糊综合评价中隶属函数，克服评价语言值中的模糊性，使结果更加可靠。

3.1.1 云模型定义

定义：假设定量论域U，C为U中的定性概念，则U中定量值x对于定性概念C的确定度为μC(x)，且μC(x)∈[0，1]。μC(x)在论域U上的分布称为云，x称为云滴。云作为定量论域U到区间[0，1]的映射，数学表达式为

μC(x):U→[0，1]，∀x∈U，x→μC(x)

(6)

云的数字特征参数由期望Ex、熵En、超熵He表示，分别反映论域U中云滴分布的中间值、定性概念的模糊度和不确定度[22]，因此将云模型记为D(Ex，En，He)。

3.1.2 等级评价云特征参数

(7)

(8)

(9)

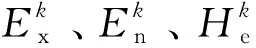
(10)

式(10)中：Kk为风险等级k评价区间边界值。

3.1.3 云发生器

3.1.4 云的集合

不同权重指标的云模型合成为一个加权云模型称为云的集合。采用虚拟云理论[24]，计算公式为

(11)

(12)

(13)

3.1.5 云的相似度

抗浮锚杆系统风险等级评价总目标加权云与各风险等级评价云之间的距离相似度将用来表示综合评价结果在不同风险等级的隶属度。设两朵云分别为Dq(Exq，Enq，Heq)(q=1，2)，其距离相似度为

(14)

式(14)中：l1= min(Ex1+3En1，Ex2+3En2)-max (Ex1-3En1，Ex2-3En2)，l2=max(Ex1+3En1，Ex2+3En2)-min(Ex1-3En1，Ex2-3En2)。

3.2 基于云模型的评价流程

基于云模型的抗浮锚杆系统风险等级评价方法流程如图4所示，具体步骤如下。

步骤1邀请专家对各个指标的重要程度进行打分评判，并利用ANP法和熵权法确定主客观权重，并应用博弈论理论对权重进行组合优化。

步骤2根据风险等级评价标度区间划分，应用式(7)～式(9)得到不同风险等级评语云模型。

步骤3邀请专家对各指标进行风险程度评价，应用逆向云发生器将评价数据转化为评价指标云。

步骤4将各个指标云模型结合指标权重应用式(11)～式(13)得到风险等级评价总目标综合云模型，并结合不同风险等级评语云模型通过正向云发生器生成风险等级综合评价云滴图。

步骤5应用式(15)计算综合评价结果在不同风险等级区间的隶属度，根据最大隶属度原则得到最终风险等级S。

S=max{S(D，DⅠ)，S(D，DⅡ)，S(D，DⅢ)，

S(D，DⅣ)，S(D，DⅤ)}

(15)

图4 抗浮锚杆系统风险等级评价流程图Fig.4 Flowchart of risk level evaluation of anti-floating anchor system

4 工程应用

以某商业广场项目抗浮锚杆系统为例，其C区由三栋写字楼及购物中心组成，建筑面积达到260 000 m2。地下2 层主要为设备、电器用房及车库等，场区地下水为潜水类型。近3～5年历史最高水位黄海高程约为1 108 m，含水层主要为粉细砂层，渗透系数为0.87×10-3～4.96×10-3cm/s，属于强透水层。

邀请5位具有地下结构工程领域专家对项目工程现场调研，结合专家打分法，对该抗浮锚杆系统中各评价指标的风险等级进行评判。

4.1 指标权重确定

通过5位专家进行指标的重要程度进行打分并构建评判矩阵，利用ANP法计算各指标主观权重，然后用熵权法确定其客观权重，应用基于博弈论中纳什均衡进行组合优化，最终各指标组合权重如表2所示。根据式(4)、式(5)得出ANP法确定的主观权重系数为0.588 1，熵权法确定的客观权重系数为0.411 9，说明通过博弈论的纳什均衡使得客观赋权对专家评判得到的主观权重起到了修正作用。抗浮锚杆系统风险影响因素重要度排序为抗浮水位风险A22、抗浮稳定性风险A23、施工规范程度A31、勘测设计风险A21、工人综合素质风险A34、地表及地下水渗流风险A12、地层岩性风险A11、安全监管风险A42、施工技术风险A32、抗浮锚杆质量风险A33、极端降水天气A13、抗浮锚杆设计风险A24、安全教育风险A41、管理人员综合素质A43。

4.2 确定评价综合云模型

4.2.1 系统风险等级评价云模型确定

为与云模型衔接，不同标度区间按式(7)～式(9)转化为等级评价云模型，见表3。设置云滴数为2 000，并绘制等级评价云图，如图5所示。

表2 各级指标综合权重Table 2 Comprehensive weight of indicators at all levels

表3 不同等级评价云模型Table 3 Cloud models with different levels of evaluation

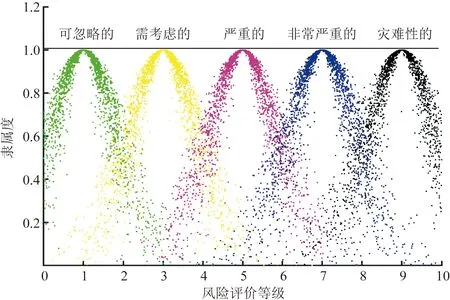
图5 不同风险等级评价云滴图Fig.5 Cloud drop diagram of comments on different risk levels

4.2.2 计算指标云模型

根据5名专家对评价指标风险程度进行打分，其中5个等级分别对应数值(9，7，5，3，1)，其余数值表示指标等级介于两相邻等级之间。将各指标赋值情况，通过逆向云发生器计算得到各二级指标的云模型，如表4所示。

表4 二级指标云模型汇总Table 4 Summary of secondary indicator cloud model

4.2.3 确定综合评价云模型

将得到的二级指标云模型与其对应的组合优化权重根据式(11)～式(13)进行综合云计算，从而得到抗浮锚杆系统风险等级评价的一级指标和总目标云模型参数分别为

根据总目标云模型和等级评语云模型，利用MATLAB2017a软件设计云正向发生器，生成抗浮锚杆系统风险等级评价总目标的综合评价云图，如图6所示。

从图6中可看出，抗浮锚杆系统风险等级评价总目标的云滴(红色)大部分落在“需考虑的”区间中，少部分落在“严重的”的区间。因此专家组对该系统风险等级评价结果为“需考虑的”等级。

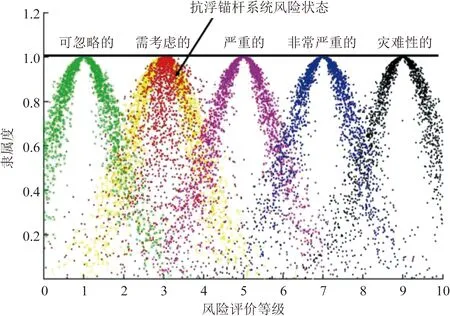
图6 抗浮锚杆系统风险等级综合评价云滴图Fig.6 Cloud drop diagram for comprehensive evaluation of risk level of anti floating anchor system

4.2.4 综合隶属度确定

结合式(14)计算综合评价结果对于不同风险等级隶属度，其计算结果如表5所示。由最大隶属度原则可知，该抗浮锚杆系统风险等级的评价结果为Ⅱ级“需考虑的”。 根据一级指标评价云模型参数特征得到四个风险因素的风险程度排序，从大到小依次为A2、A3、A1、A4。可以看出，设计方案风险是四大风险因素中风险程度值最大的，施工质量风险次之。

借鉴文献[9]中故障树模型计算得到该抗浮锚杆系统风险发生概率为6.364%，其地下工程风险概率等级为B级[16]，属于需要考虑的风险状况，与本文评价结果一致，表明了基于系统动力学-云模型(system dynamics-cloud model，SD-CM)的风险等级评价方法可以准确合理地评价抗浮锚杆系统风险等级。

表5 综合隶属度Table 5 Comprehensive membership

5 结论

(1)通过对抗浮锚杆系统锚固界面失效机理进行系统动力学分析，得出了锚固界面子系统风险形成路径失效，在此基础上构建了以4个一级指标及14个二级指标组成的抗浮锚杆系统风险等级评价指标体系。

(2)采用了ANP法和熵权法确定各指标的主观权重和客观权重，并用博弈论理论对指标权重进行优化。

(3)根据抗浮锚杆系统风险等级评价数据，采用云模型理论处理各风险因素的模糊性，提出了基于云模型的抗浮锚杆系统风险等级评价方法。最终评价结果为Ⅱ级“需考虑的”，与系统实际风险状况相符，可为抗浮锚杆系统风险评价提供一种新思路。