浮体平台运动对浮式风电机组气动特性影响风洞试验
王新宝,李庆安,4,*,蔡 畅,王泽坤,王腾渊,陈晔雯,杨英健
(1. 中国科学院 工程热物理研究所,北京 100190;2. 中国科学院 风能利用重点实验室,北京 100190;3. 中国科学院大学,北京 100049;4. 中国船舶重工集团 海装风电股份有限公司,重庆 401122;5. 内蒙古工业大学 能源与动力工程学院,呼和浩特 010051;6. 华北电力大学 能源动力与机械工程学院,北京 102208)
0 引言
浮式风电的概念早在20世纪70年代就由麻省理工大学的Heronemus教授提出,但受技术和成本的制约,直到20世纪90年代才得到重视[1]。伴随着世界上首个浮式风电项目Hywind的建成和成功运行[2],近年来浮式风电逐渐成为风电领域和海洋工程领域的研究热点。在国内,多个研究团队对平台运动下的风电机组气动性能、缩比试验技术、多体多场耦合演化机理、一体化仿真和设计等方面开展了相关研究,这些研究内容为扫清我国浮式风电走向商业运营的关键阻碍[3]做出了贡献。在国家重大需求的牵引下,浮式风电亟需突破技术封锁和技术瓶颈。浮式风电的成功研制及运营,对“双碳”战略目标的实现具有十分重要的意义。
浮式风电机组与固定式机组的不同之处在于,其上部机组安装在下部浮体平台上,机组运行受风-浪-流的组合扰动,处在六个自由度的运动中[4],气动-水动-伺服-弹性多体多场耦合机制极其复杂。由于受到波浪和海流的影响,机组的前后纵摇、纵荡和偏航运动显著改变了动态的功率、推力和力矩性能[5]。在仿真方面,动量叶素理论、自由涡尾迹方法被广泛应用于建立耦合数学模型,也有部分学者使用其他方法,如涡格方法和叶栅模型[6]。对于前后纵摇运动下,Shen和Li等[7-8]的计算结果表明,功率输出稍有增加,平均推力明显降低;也有仿真结果表明,功率和推力波动较大,可达32.8%[9]。在Tran和Huang等[10-11]的研究中发现,在高频和大振幅下,平台后仰可促进尾流的结合和恢复,增大机组的功率;平台前俯会引起叶片失速和振动,增加风轮的推力和扭矩,同时增强叶片与尾流的相互作用。对于纵荡运动下,Farrugia和Chen等[12-13]获得的结论为:纵荡运动会使平均功率增大,平均推力减小,但推力的波动会增加叶片、轴等部件的疲劳载荷。当纵荡振幅和频率增加时,平均功率在低叶尖速比区域会降低,在高叶尖速比区域会升高;平均推力在所有叶尖速比下都会下降;但是推力和功率的波动会明显增强。此外,纵荡振幅对尾流速度的影响大于频率的影响,同时Wen和Shen等[14-15]将其整合到降低的频率中进行了分析。
浮式风电机组的模型试验可以在波浪水池或风洞中进行,现有研究大部分试验是在水池中开展的,以研究浮体平台和系泊系统的运动响应和载荷传递规律。其中,上部风电机组可以是原型机组按照相关相似准则缩尺后的模型,也可以是能够模拟上部空气动力学效应的仿真模块[16-17]。上海交通大学、中国科学院工程热物理研究所、华北电力大学、哈尔滨工业大学、哈尔滨工程大学、天津大学等研究团队,分别基于水池实验室和风洞实验室开展了复杂海洋环境下的浮式风电机组混合模型试验技术研究[18],初步建立了浮式风电机组模型的缩尺理论、模型设计、状态监测与性能评估方法,为浮式风电机组多体多场机制和协同控制研究提供了技术基础和平台支撑。Meng等[19]在水池中研究了不同波浪和风况条件下机组模型的运动响应,分析了多体多场耦合机制下的水动力学行为。Khosravi[20]测量了纵荡运动下的气动特性和尾流特性,发现疲劳载荷显著增加,浮体平台的运动影响了尾流的湍流掺混过程。南京航空航天大学团队研究了台风过境过程中大型水平轴风电机组的极端载荷[21],以及海洋运动对风速的影响规律[22],为大型浮式机组抗强台风设计提供了参考依据。但是风电机组作为功率捕获最直接的部件,其气动特性和动态载荷直接影响到供电稳定和机组的疲劳寿命,因此有必要开展浮式风电机组在浮体平台运动下的气动特性试验研究。
在前人工作的基础之上,作者团队进行了浮式风电机组模型在纵摇单自由度运动下的气动特性试验研究。其中,浮体平台的运动由六自由度平台模拟,机组的功率和载荷特性由机舱内扭矩传感器和塔顶六分力天平分别测量。试验分别在静态和动态的条件下进行,以获得风轮俯仰力矩和偏航力矩的动态波动特性,定性地分析浮体平台的纵摇运动对载荷波动的影响规律。研究结果有助于浮式风电机组效率和稳定性的自适应控制技术开发。
1 试验仪器与方法
浮体平台的纵摇运动会显著影响风电机组的气动特性。本文进行了不同纵摇振幅和定常风速工况下的试验研究,目的是分析浮式风电机组的功率和气动载荷的动态变化特征。
1.1 试验仪器
1.1.1 风洞
试验在低速回流式风洞中进行,风洞示意图见图1。风洞出口直径为3.6 m,测试段长度为4.5 m。来流经过蜂窝网状整流罩整流后具有均匀的速度分布,风洞中心高度处的速度分布偏差在1.5%以内,满足30 m/s以下的定常风速条件。
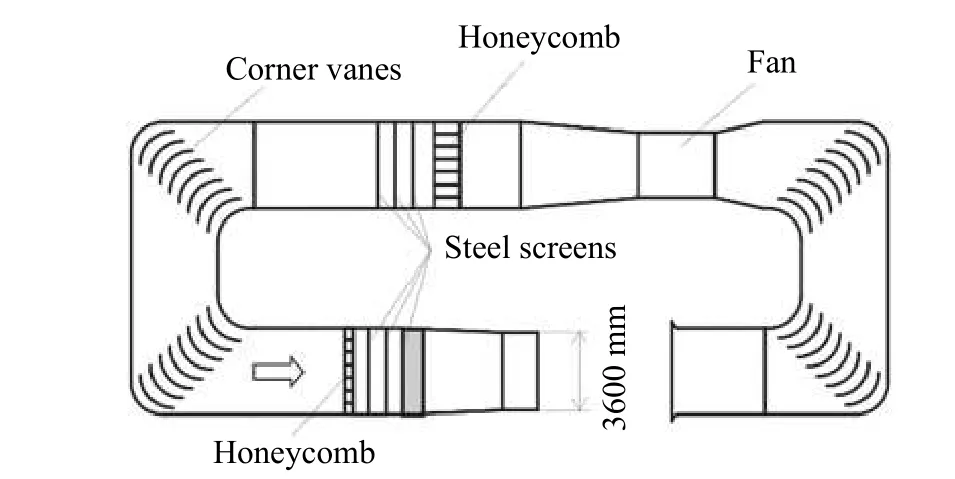
图1 风洞俯瞰示意图Fig. 1 Sketch of wind tunnel
1.1.2 模型风电机组
试验用机组模型为水平轴上风向三叶片机组,单个风力机直径为1.6 m。整个叶片根据叶素动量理论设计,为低雷诺数下气动性能较优的Avistar单翼型分布。就单叶片而言,从上方的竖直状态开始,顺时针旋转一周,其方位角从0°变化至360°;平台纵摇角度以水平状态为0°基准,后仰为正;纵摇运动中心为浮体平台摆动的中心。
1.1.3 传感器
试验用传感器包括用于监测扭矩变化的扭矩传感器和用于监测力矩动态特性的六分量天平。扭矩传感器量程为10 N・m,精度为0.5%,采集频率为50 Hz。六分力天平力矩测量的量程及绝对误差分别为50 N・m和0.25 N・m。俯仰力矩正方向定义为机组后仰的方向,偏航力矩方向与机舱偏航方向一致。
1.1.4 六自由度平台
试验用六自由度平台与机组模型的塔底相连(图2),设置在距风洞出口2.3 m处,可实现特定周期和振幅的纵摇运动,旋转角精度和位移精度分别为0.05°和0.05 m。

图2 浮式风电机组模型系统Fig. 2 Floating turbine model
1.2 数据处理方法
1.2.1 机组模型气动性能数据
计算风轮所受的力矩时,主要关注俯仰力矩和偏航力矩性能。计算时,需要对塔顶处的测量结果进行修正,进而得到风轮处的力和力矩特性。
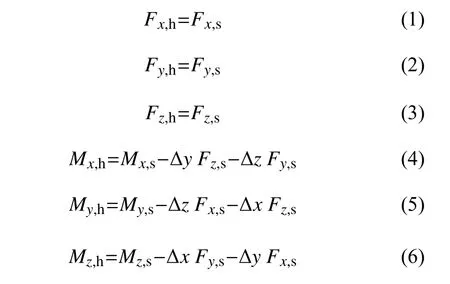
式中:Fx,s、Fy,s、Fz,s、Mx,s、My,s、Mz,s分别为机舱底部实 测 的 三 个 轴 向 的 力 和 力 矩,Fx,h、Fy,h、Fz,h、Mx,h、My,h、Mz,h分别为修正后的三个轴向的力和力矩。∆x、∆y、∆z分别为修正位置到六分力天平测点的坐标值。
测量得到风轮扭矩、俯仰力矩和偏航力矩后,通过下式计算相应的无量纲系数。

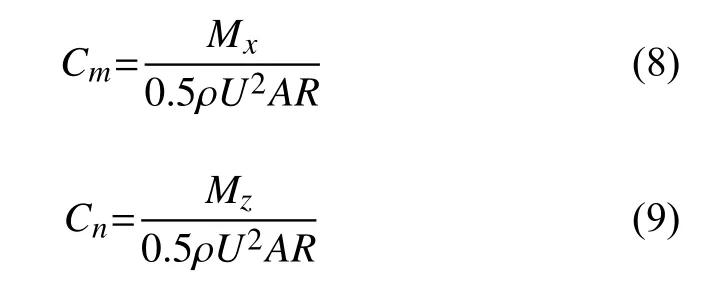
式中:CP、Cm和Cn分别为功率系数、俯仰力矩系数和偏航力矩系数,ω为模型风轮转速,U为风速,Q为扭矩传感器测得的扭矩值,ρ为空气密度,A为风轮扫掠面积,Mx为俯仰力矩,Mz为偏航力矩,R为风轮旋转半径。图3给出了天平载荷定义示意图。
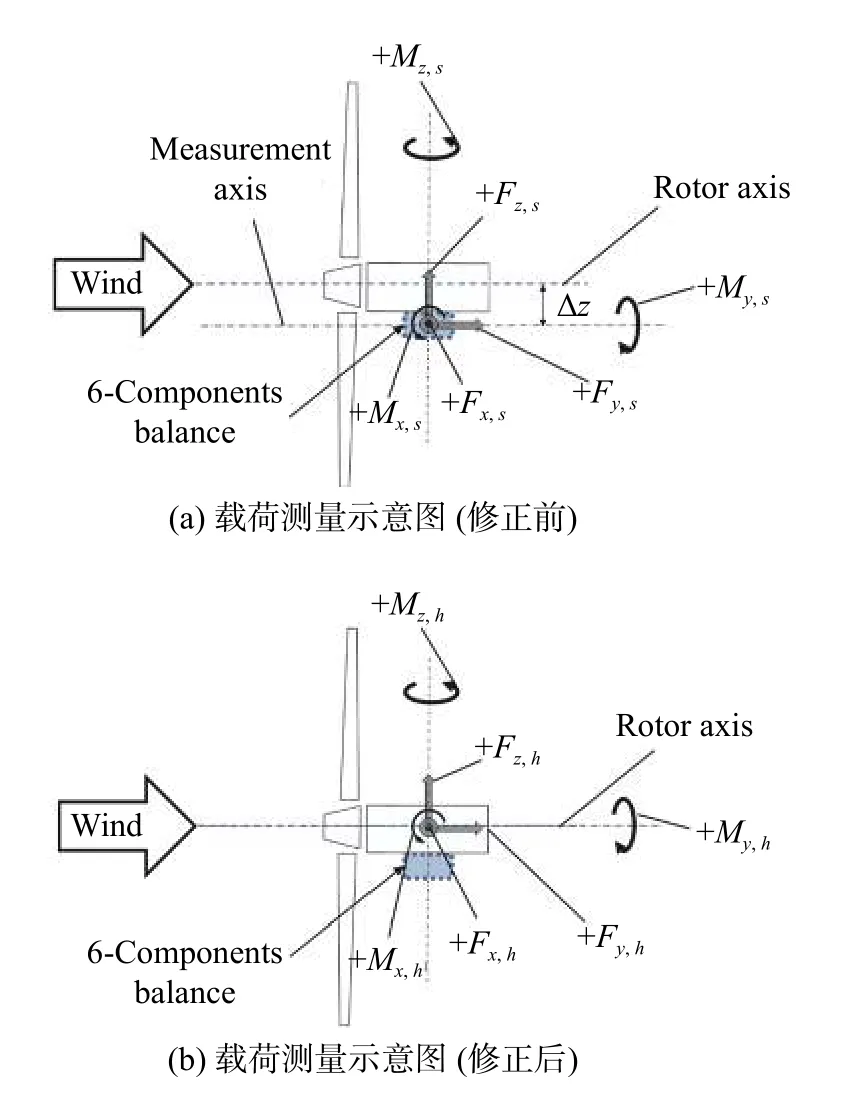
图3 载荷分布与测量Fig. 3 Load distribution and measurement system
1.2.2 六自由度平台纵摇运动数据
浮体平台纵摇运动呈现正弦曲线规律,在给定纵摇中心角、振幅和周期之后,其纵摇角度随时间变化的公式如下:
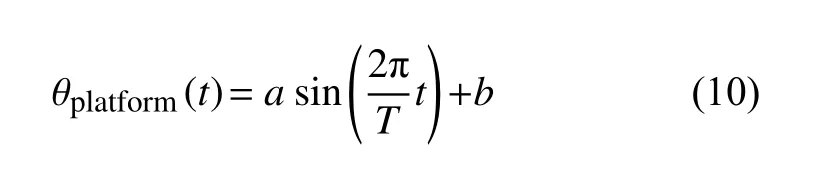
式中:a为平台纵摇振幅,b为纵摇中心角,T为纵摇周期,t为时间。
试验开展前,需要确定机组模型纵摇运动的特征周期。首先根据NREL 5 MW机组额定工况运行和纵摇单自由度运动下的时间历史曲线进行时空变换,得到纵摇运动的频谱(如图4所示)。分析可见,实际机组纵摇运动下的第一峰值频率为0.0347,第二峰值频率为0.125。选取第一峰值频率0.0347作为试验条件,即纵摇运动周期为28.82 s,根据相似变换准则得到机组模型的纵摇频率(即纵摇周期),变换公式如下:
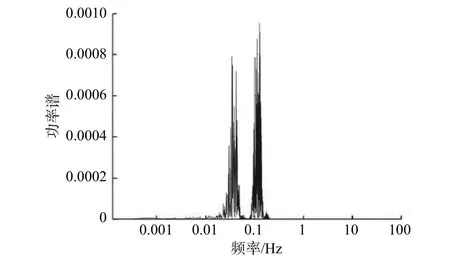
图4 原型机组纵摇运动频谱Fig. 4 Pitching motion spectrum of the prototype turbine

其中:Tmodel和Tactual分别为机组模型和原型机组的纵摇周期,Rmodel和Ractual分别为机组模型和原型机组纵摇运动的半径。经上述变换之后的机组模型特征纵摇周期为2.821 s,以此作为机组模型试验的纵摇运动周期的工况。
2 气动性能测试
进行了不同风速和不同平台纵摇运动状态下的气动性能测试,目的是确定试验风速,并获得不同纵摇角度下的功率曲线。
2.1 不同风速下的气动性能
首先进行了定常风速下的气动性能测试,风速分别为6 m/s、8 m/s、10 m/s,获得了功率系数随叶尖速比变化的规律,如图5所示。由图可见,随着叶尖速比的增加,功率系数先增大然后逐渐减少,并且随着风速的增加,功率系数也略有增大。在低叶尖速比区域,随着转速增加,叶尖速比增大,攻角不断减小,叶片逐渐脱离失速状态,功率系数明显上升;在超过最佳叶尖速比之后,随着转速继续增加,攻角继续减小,叶片升力降低,阻力升高,功率系数明显降低。当来流风速为10 m/s时,可获得最大功率系数(0.427)。
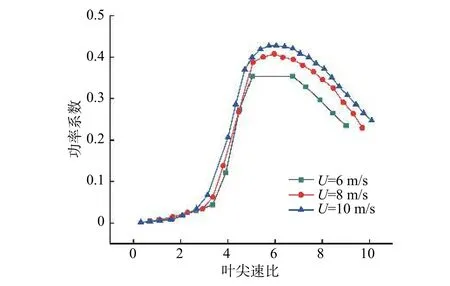
图5 不同风速下的功率系数曲线Fig. 5 Power coefficients at different wind velocities
2.2 不同平台纵摇角度下的气动性能
来流风速为10 m/s时,分别进行了平台纵摇角度0°、5°、10°状态下的气动性能测试。试验中不涉及变桨和平台的动态运动过程。获得了功率系数随叶尖速比变化的规律,如图6所示。可以看出,功率系数随叶尖速比先增大然后逐渐减少,并且在高叶尖速比区域随着纵摇角度的增加而略有降低。在纵摇角0°和叶尖速比5.7时,可获得最大功率系数(0.426)。此外,平台纵摇角度的增加及机组的倾斜使叶片进入偏航状态,一方面风轮扫风面积减小,另一方面可能存在与偏航工况类似的动态失速效应,机组的气动性能受到明显影响。

图6 不同平台纵摇角度下的功率系数曲线Fig. 6 Power coefficients at different platform pitch angles
3 力矩性能测试
静态测试结果表明,风速的增加和平台纵摇角度的减小均能增大功率系数。动态运动测试的试验风速设定为10 m/s,并以静态测试结果为基础来进行数据的对标与分析。在气动性能测试基础上,设置风速为10 m/s、叶尖速比为5.7,进行了纵摇单自由度下的静态和动态试验,目的是分析机组模型的风轮俯仰力矩和偏航力矩的静态变化计动态波动特性。
3.1 静态测试
在风速为10 m/s、叶尖速比为5.7工况下,调节平台的纵摇角度,测量了纵摇角度0°~10°(间隔1°)范围内的俯仰力矩和偏航力矩,结果如图7所示。可以看出,随着纵摇角度的增加,力矩系数值不断增大。由于不涉及变桨,攻角取决于入流角值。平台纵摇角度增加,风轮整体倾斜,入流角减小,气动力更偏于推力的方向,俯仰力矩增大。偏航力矩值可能与风轮旋转方位角以及平台的倾斜状态有关。
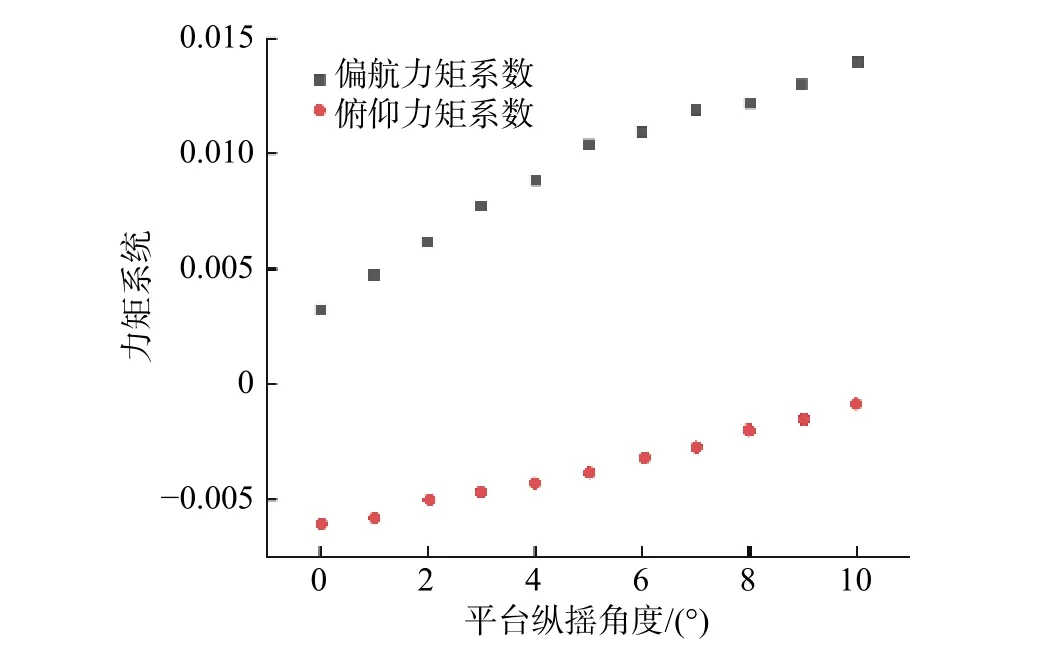
图7 不同平台纵摇角度下的俯仰和偏航力矩系数Fig. 7 Pitching and yawing moment coefficients at different platform pitch angles
3.2 动态测试
在静态测试的基础上,进行了不同纵摇振幅下的动态性能测试,并与静态测试下的结果作对比,以分析偏航力矩和俯仰力矩的动态波动规律。
图8 显示的是纵摇周期2.821 s、纵摇中心角5°、纵摇振幅分别为1°、3°、5°时的俯仰力力矩和偏航力矩系数的动态变化曲线,图中红色、绿色和蓝色的点表示平台前俯状态(即纵摇角度增大的方向),灰色点为平台后仰状态(即纵摇角度减小的方向),黑色的星形点表示静态测试下的结果。可以看出,纵摇角度增大,力矩系数值增加,但是在平台前俯和后仰时的力矩值并不相同,表现出明显的迟滞效应,并且偏航力矩的迟滞环是逆时针方向,俯仰力矩的迟滞环是顺时针方向。并且随着纵摇振幅的增加,迟滞效应更加明显。此外,偏航力矩系数围绕静态测试点值上下波动,而俯仰力矩系数均高于静态测试点值。
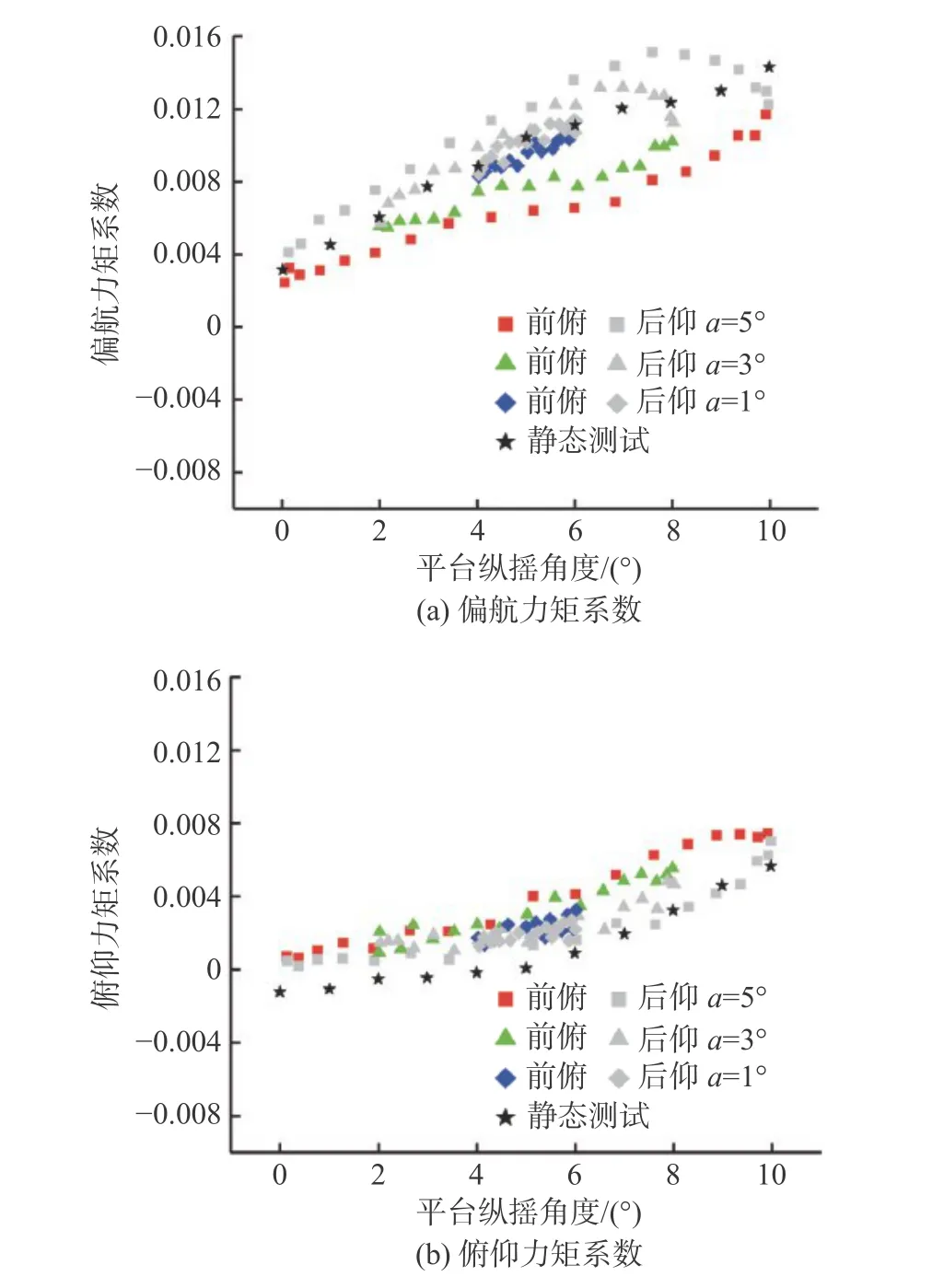
图8 不同摆动振幅下的偏航和俯仰力矩系数Fig. 8 Pitching and yawing moment coefficients for different pitch amplitudes
力矩性能测试结果表明,纵摇振幅会增大俯仰力矩和偏航力矩波动极值,纵摇中心角会改变俯仰力矩和偏航力矩的平均值。平台纵摇运动会显著影响风轮的偏航力矩和俯仰力矩,造成力矩波动,加剧叶片的疲劳载荷,影响机组的使用寿命和运行稳定性。因此,在进行浮体平台设计时,有必要增大惯性或施加针对性控制,以减小纵摇运动下的振幅,提高机组运行的稳定性和安全性。
4 结论
浮式风电机组在风-浪-流组合扰动下的气动-水动-伺服-弹性多体多场耦合机制研究,需要气动特性试验作为支撑。针对该情况,开展了纵摇单自由度运动下浮式风电机组模型风洞试验,获得了功率系数曲线,分析了平台纵摇振幅对风轮俯仰力矩和偏航力矩波动的影响。主要结论如下:
1)静态测试下,平台纵摇角度的增加会降低功率系数,同时会增大俯仰力矩系数和偏航力矩系数。
2)动态测试中,纵摇运动会造成风轮气动载荷的波动。纵摇振幅增大时,迟滞效应增强,风轮疲劳载荷加剧,纵摇中心角会改变俯仰力矩和偏航力矩的平均值。
本文研究的浮体平台运动下浮式风电机组的气动特性规律,对于厘清风-浪-流组合扰动下风电机组的气动-水动-伺服-弹性多体多场耦合机制具有重要意义,有助于提升效率和稳定性的自适应控制技术的开发。

