基于风洞试验15 MW风力机叶片颤振后形态与能量图谱研究
柯世堂,陆曼曼,吴鸿鑫,2,高沐恩,田文鑫,王 浩,王 硕
(1. 南京航空航天大学 土木与机场工程系,南京 211106;2. 南京航空航天大学 江苏省风力机设计高技术研究重点试验室,南京 210016;3. 河海大学 力学与材料学院,南京 211100)
0 引言
随着超大功率风电机组的发展,风力机叶片愈发趋向超长柔细化演变,由此带来的气动/结构双重非线性导致风力机叶片振动问题突出[1-3],尤其是失稳性颤振问题亟需解决。近年来,在强台风等恶劣天气条件下,大型风力机叶片颤振风毁事故[4-6]频发,如2003年台风“杜鹃”和2006年台风“桑美”导致的风电场内大面积风力机组受损事件等。并且,大型风力机叶片颤振后的非线性行为更为显著。传统的风力机叶片颤振分析方法(如:多参数法[7]、模态分析法[8]、特征值法[9]等),多为针对风力机叶片颤振临界状态的研究,无法解释在颤振临界点后发生的稳定振幅振动现象。因此,超长柔性叶片颤振后形态与能量耗散机制的研究具有重要理论意义。
颤振后形态,一般是指颤振临界风速后的振动形态及结构力学性能,极限环振动现象是最为常见的颤振后非线性振动现象[10]。现有关于颤振后形态的研究聚焦于壁板[11]、机翼[12]和桥梁[13]等结构,大多是基于风洞试验方法建立数学模型,以考虑各种非线性因素在颤振后状态中所产生的影响[14]。风洞试验是研究强非线性运动机理及能量集聚特性的最有效手段之一,但是由于风力机叶片翼型不规则,其截面、刚度、剪心等沿展长不规则分布使弹性模型设计难度大,大缩尺比带来测点布置难、采集干扰性强、测量精度低等试验困难,导致国内外较少开展超长柔性叶片三维颤振弹性模型试验研究。试验中一般采用二维翼型进行测压、测力试验[15-18],试验验证了二维翼型测压、测力结果的一致性,为后期振荡翼型的风洞试验研究提供了新方法,但二维翼型的研究结果无法完整反应三维超长柔性叶片的气弹失稳性能。在数值模拟方面,Yu等[19]基于CFD-CSD耦合方法,发现叶片气动扭转变形对非定常动载荷影响显著,但松耦合精度较低,滞后效应明显;黄俊东等[8,20]采用“超级单元”并考虑了刚柔耦合及非定常气弹耦合效应,发现颤振失稳时振型由单向振动演变为多方向振动。
本文以NREL-15 MW超长柔性风力机叶片为对象,基于运动等效提出了风力机超长柔性叶片合理简化相似准则,并结合变分渐进梁截面法(VABS)[21],完成了叶片气动-刚度-质量分布缩尺映射的弹性模型设计,然后通过非接触高速摄像进行了风力机叶片同步测振、测力风洞试验。系统讨论了不同风向角与风速作用下的叶片风振特性,提炼出了风力机叶片风振敏感风向区间与临界风速组合规律,基于模态分析法研究了其颤振稳定性能,并提出了一种基于能量演变效应的风力机叶片颤振后研究方法。
1 超长柔性叶片弹性模型设计
1.1 叶片参数
以美国可再生能源实验室研发的15 MW风力机超长柔性叶片作为风洞试验的弹性模型研究对象。模型质量65.252 t,模型轮毂高度150 m,直径7.94 m,风轮直径240 m。叶片采用DTU FFA-W3系列翼型。叶片全长117 m,叶根直径5.2 m,叶尖预弯4 m,最大弦长(5.77 m)出现在23.3%展长(27.2 m)处,质心位于22.9%展长(26.8 m)处。风力机叶片几何参数见表1。

表1 15 MW级风力机叶片几何参数列表Table 1 List of geometrical parameters of a 15 MW wind turbine blade
1.2 气弹试验模型设计方法
结构动力学相似和气动外形相似是弹性模型设计的基本原则[22]。超长柔性风力机叶片气动弹性模型的设计和制作须满足空气动力几何相似、结构固有模态相似和阻尼特性相同,需模拟的相似参数有:雷诺数(Re)、柯西数(Ca)、弗洛德数(Fr)、密度比以及阻尼比等。风力机叶片所在流场为低速、牛顿黏性流、不可压流场,流体运动方程与结构运动方程为:
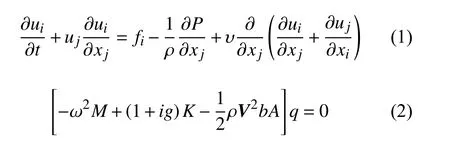
式中:u为流体运动广义速度;f为流体广义外力;ρ为空气密度;P为压强;υ为空气运动黏度,υ =μ/ρ;ω为锁频风振频率;M为广义质量;K为广义刚度;g为阻尼系数;ρ为大气密度;V为流场速度矩阵;b为参考长度;A为广义空气动力系数;q为广义坐标。
实际缩尺模型试验中的雷诺数相似很难满足,现有研究[23]发现因流场的“自模性”特征,当气动弹性试验的雷诺数大于4×105后,流场的湍流度和流速分布不再随雷诺数的增加而变化,可以满足雷诺数效应等效。基于简化相似准则的弹性模型设计仅需要满足外形几何参数、质量、刚度及阻尼比的相似,考虑阻塞比对试验结果的影响,因此模型几何缩比选为1∶70,其余无量纲参数由相似准则推算而得,具体风力机叶片弹性模型相似参数见表2。
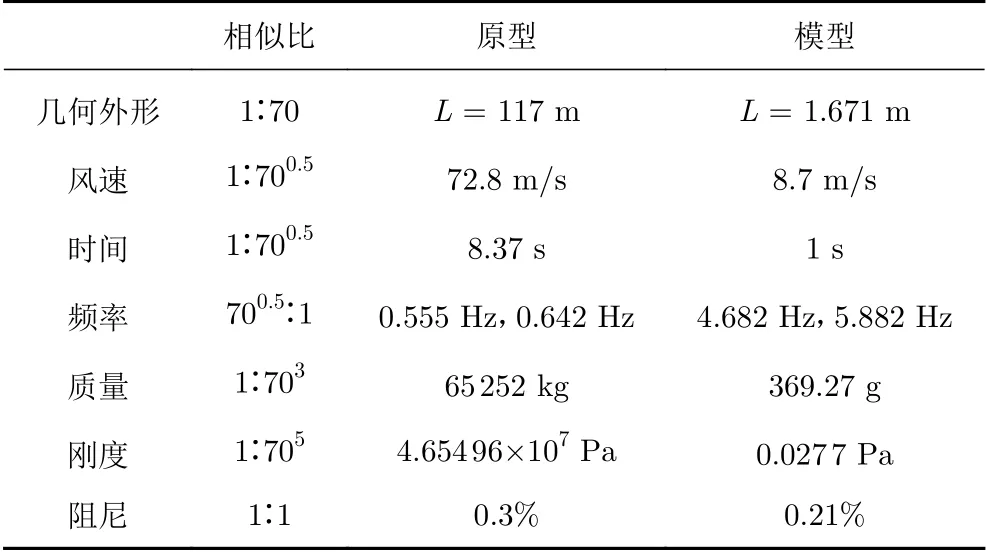
表2 模型相似比Table 2 Similarity ratios
综合考虑相似参数模拟与模型加工难度,采用VABS理论提出的等效梁截面法进行风力机叶片弹性模型的设计。为了准确模拟原型风力机叶片的刚度沿展长变化规律,并同时实现缩尺模型三向(挥舞、摆动和扭转)刚度的分别对应,等效刚度梁截面采用异形变截面十字形。由于风力机叶尖缩尺模型尺寸极小,等效刚度梁截面在满足尺寸要求时不足以提供相对刚度,故在风力机叶片相对展长80%的位置不再设置等效刚度梁截面,刚度由加强肋提供。风力机叶片弹性模型结构理论刚度与实际刚度对比及等效刚度梁截面形状如图1所示。
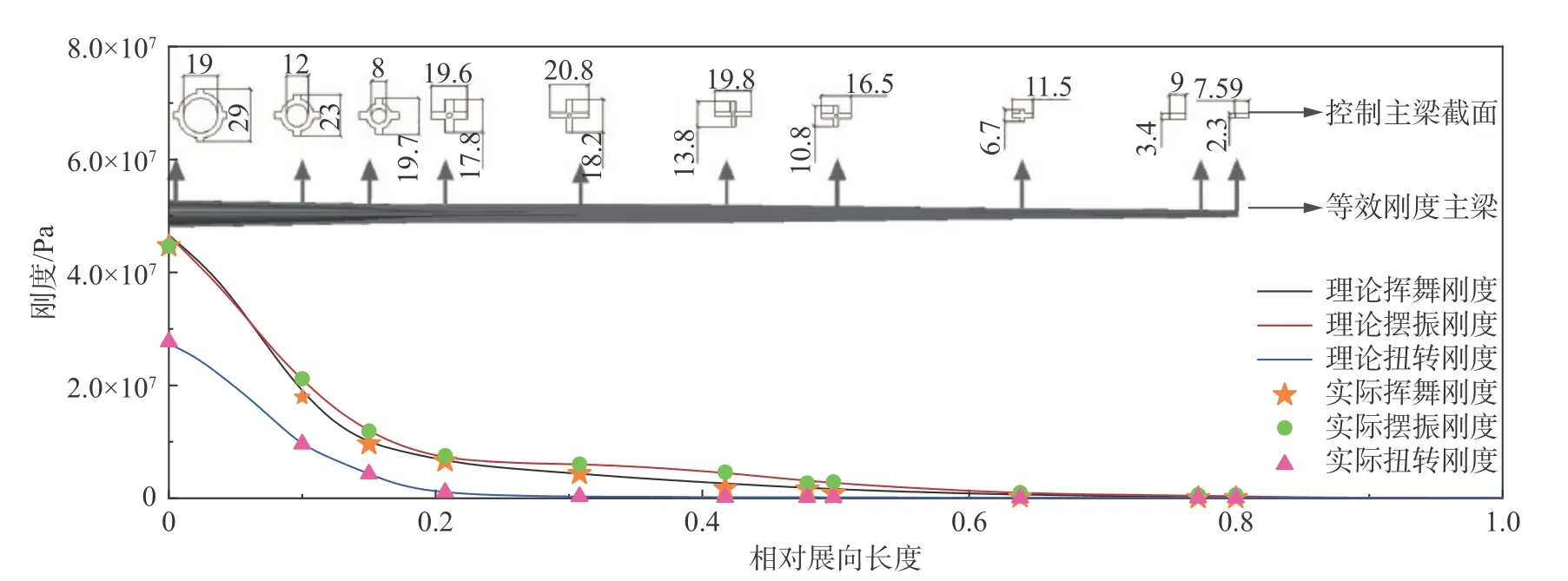
图1 叶片弹性模型主梁理论与实际刚度对比Fig. 1 Comparison of theoretical and actual stiffness of the blade girder
图2 给出了三维超长柔性叶片弹性模型结构制作示意图。模型整体采用“主梁 + 维形框段”的结构形式,承载能力由聚酰胺纤维主梁(变截面异形梁)提供。框段和主梁采用单点联接,整体打印三维框架,相邻框段间设置3 mm间隙,分段缝隙填充高密度泡沫来进行阻尼补偿并防止振动过程碰撞导致附加刚度增加。模型外部采用轻质木片填充分段前缘、后缘与檩条,保证气动外形,通过质量块调整配重使模型的质心和转动惯量模拟满足设计要求。

图2 叶片弹性模型整体制作示意图Fig. 2 Sketch of the manufacture process
1.3 结构模态分析
为验证叶片弹性模型与原型的结构运动相似性,基于锤击法测量模型的固有频率,并采用随机减量法[24]识别结构模态参数。表3为模型振型图,表4为模型与原型结构动力特性对比表。NREL-15 MW风力机预研报告[25]仅给出了前两阶模态频率,本文基于锤击法有效识别了前四阶模态,其余阶理论模态采用有限元模态分析获得。分析发现,原型与有限元模型、弹性模型的各阶模态固有频率基本吻合,基阶模态误差仅为1.8%,前四阶模态最大误差为9.5%,有效保证了弹性模型颤振特性与原型之间的相似精度。
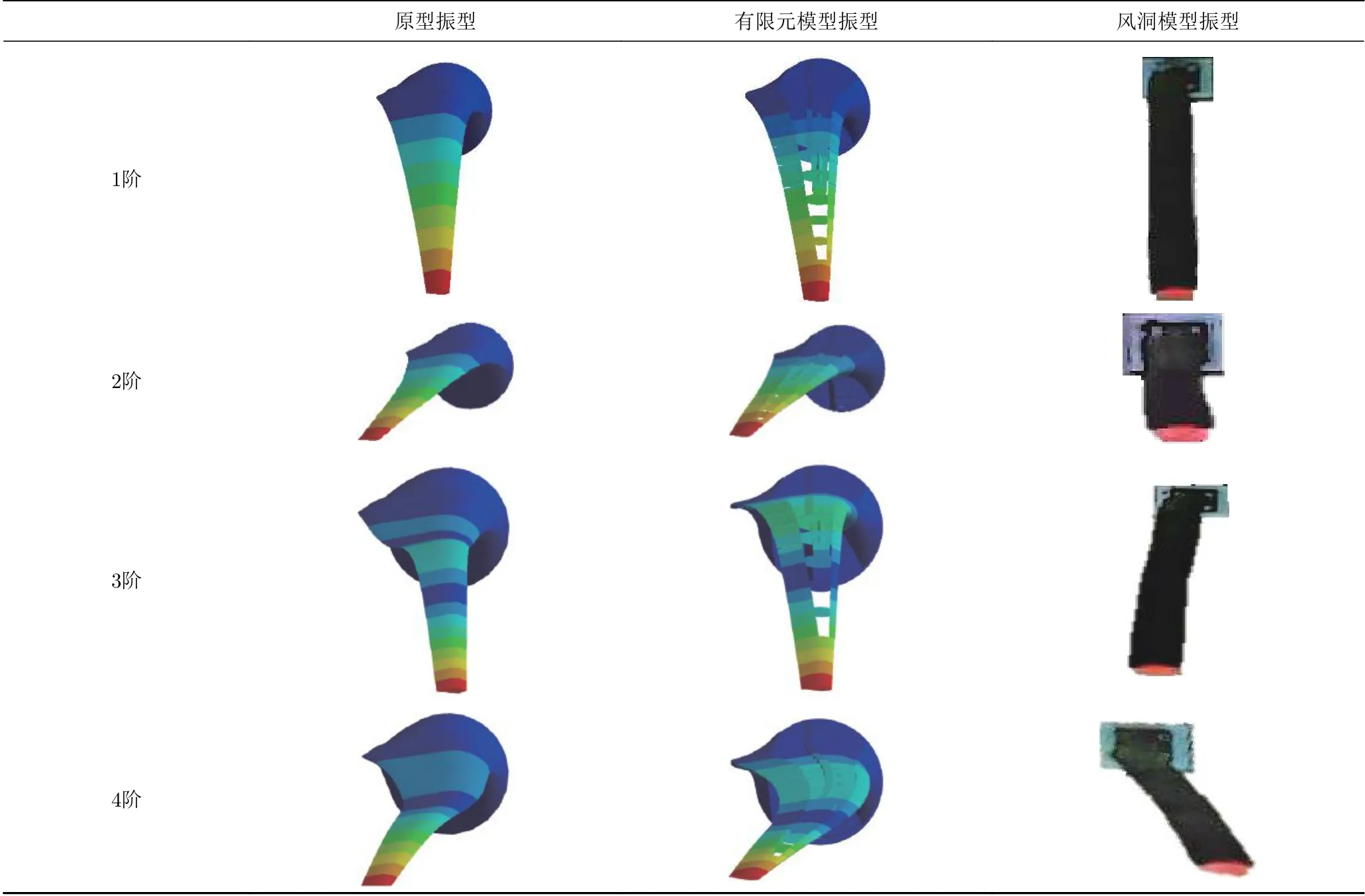
表3 模型阵型图Table 3 Model vibration mode

表4 弹性模型与原型的结构动力特性Table 4 Natural frequencies of the full-scale blade, aeroelastic model and scaled blade
2 风洞试验与结果分析
2.1 工况设置与测量系统
风洞为中国国电环境保护研究院回流式风洞,其试验段长20 m、宽2.5 m、高2 m,最大试验风速为50 m/s。弹性模型风洞试验方案如图3所示。因风力机在正常工作风速区间内不会发生颤振失稳问题,故选取停机状态下最不利的竖直叶片工况进行研究。定义垂直叶片预弯方向为来流风0°方向,顺时针旋转为角度正方向。共取36个风向角,每个风向角测量7个风速工况。
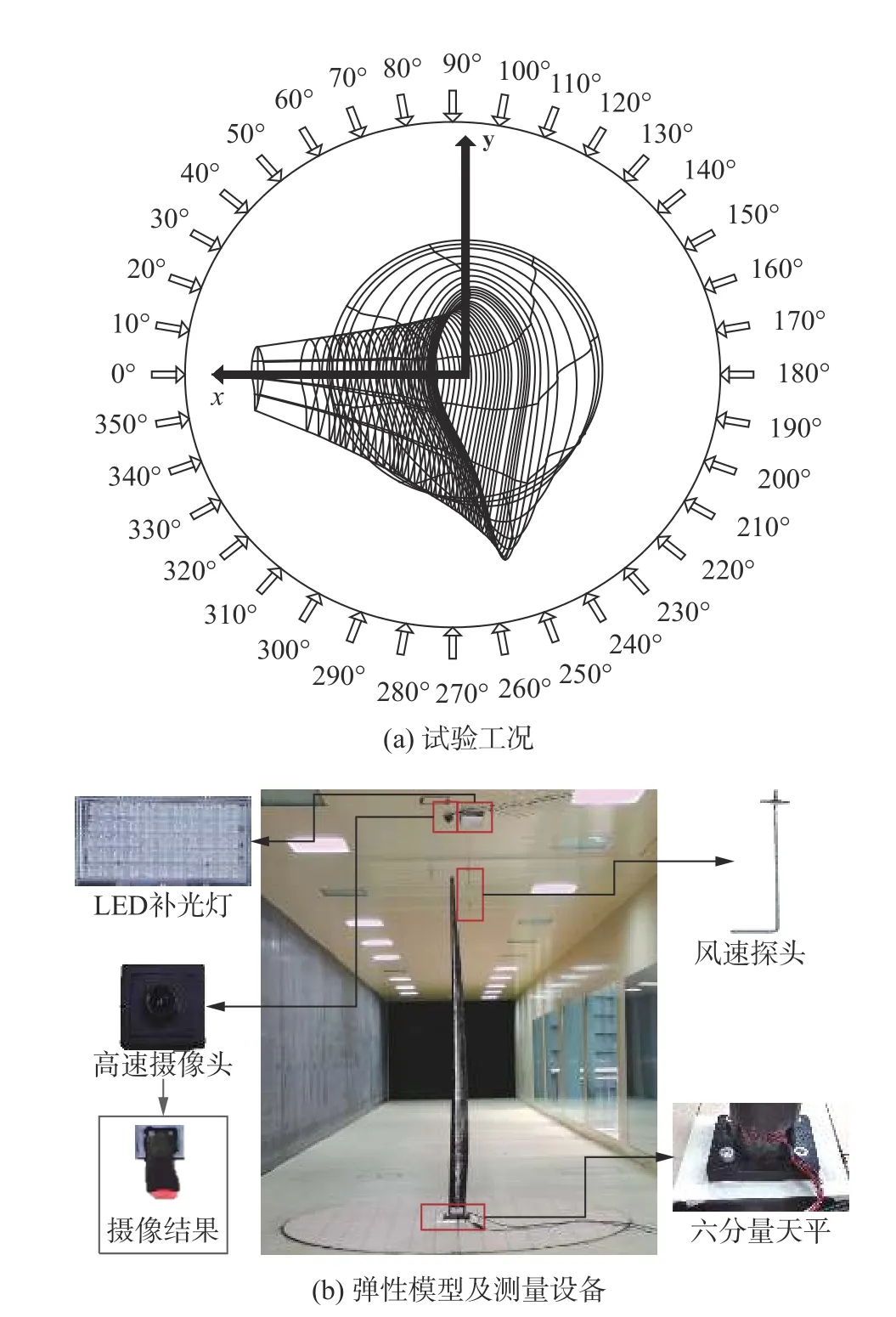
图3 叶片弹性模型风洞试验方案Fig. 3 Experimental setup in a wind tunnel
2.2 风场模拟有效性验证
图4 给出了机舱以上竖直叶片剪切风场模拟结果。由图中平均风剖面、湍流强度剖面和脉动风谱结果可见,剪切风场吻合度较好,仅在叶根区域受限于风洞壁面影响存在微小误差,风洞脉动风谱与Karman谱吻合良好。
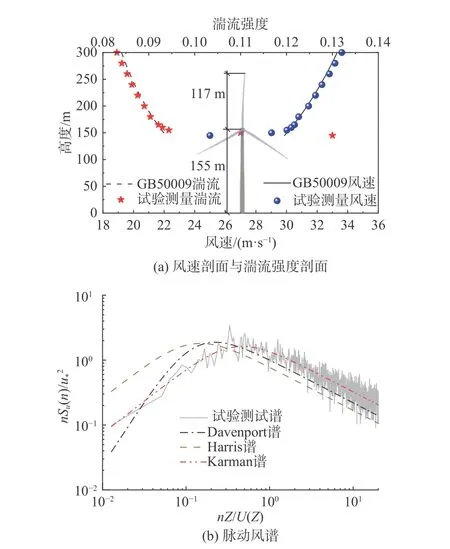
图4 初始风场定义有效性示意图Fig. 4 Effectiveness diagram of initial wind field definition
2.3 颤振区间确定
图5 给出了风洞风速7.1 m/s和8.7 m/s(实际风速为59.4 m/s和72.8 m/s,根据气弹模型的相似准则可知风速比为1:700.5,即实际风速应为风洞风速的700.5倍)时不同桨距角下叶尖挥舞、摆振位移均方根变化曲线。由图可知,当桨距角位于93°~96°及284°~287°区间时,叶尖位移均方根突增,挥舞均方根最大值分别出现在桨距角94°和286°;其他桨距角叶尖位移均方根在0~0.2 cm幅值附近波动,无明显激变,表明桨距角93°~96°及284°~287°区间内发生颤振。
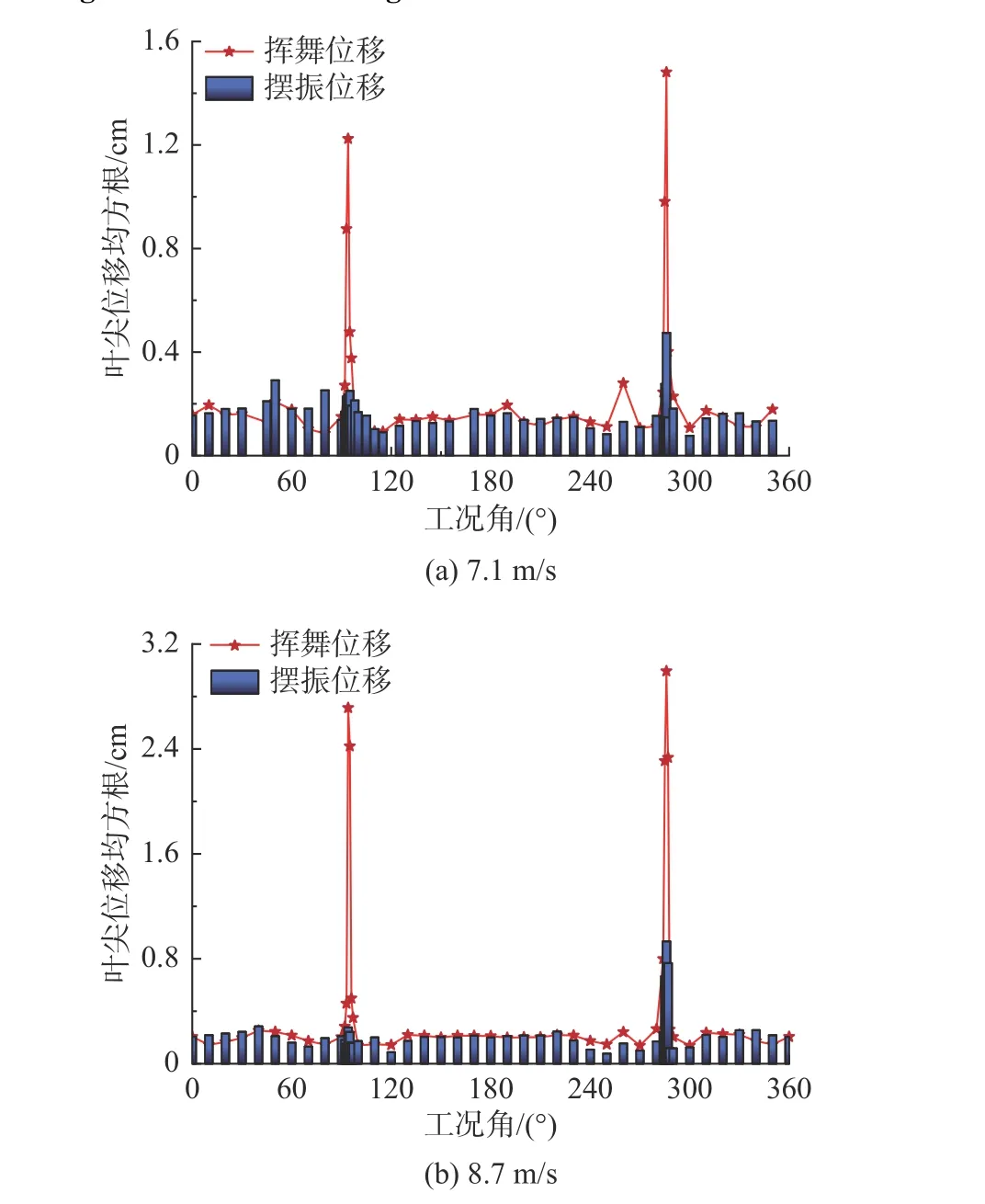
图5 不同桨距角叶尖挥舞、摆振位移均方根变化曲线Fig. 5 Variations of root-mean-square values of the blade flapwise and edgewise tip deflections with pitch angle
3 颤振后形态及能量图谱研究
颤振后形态是指颤振临界风速后的振动形态及结构力学性能,颤振临界风速是评价颤振后形态的结构性能的关键指标,能量图谱亦可描述结构振幅与特定风速内风致振动的能量特性。因此,本文着重开展了叶尖风振响应、颤振临界风速、气动阻尼比随风速变化特性研究,以及颤振后风致振动作功效应的能量图谱演变研究。
3.1 颤振后形态
图6 和图7分别为桨距角286°叶尖摆振和挥舞位移振动幅值时程曲线及不同阶段位移功率谱。由图可知,发生颤振时,叶尖位移随时间共经历三个阶段:第一阶段为短时蓄振阶段,风力机叶片积累能量,表现为无规则抖振;当风力机叶片积累一定能量后进入发展阶段,叶尖位移随时间呈现发散趋势;第三阶段为稳定阶段,当叶尖位移发散进入一定值附近后,表现为简谐振动的“软颤振”[26]。风力机叶片在发生颤振的三个阶段过程中,功率谱主导频率幅值随阶段演变逐渐变大,而主导频率随阶段演变逐渐变小并在稳定阶段达到最小,并且主导频率逐渐趋近于结构固有频率4.68 Hz。对比分析可发现,挥舞位移振幅明显大于摆振位移振幅,表明风力机叶片颤振失稳主要在挥舞方向。

图6 叶尖摆振位移三阶段时程及其功率谱曲线Fig. 6 Time histories and frequency spectra of the blade tip edgewise deflection at three stages
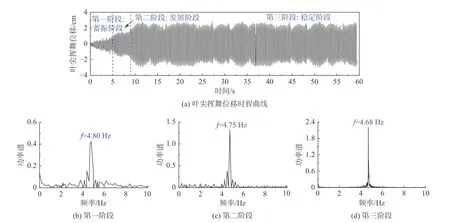
图7 叶尖挥舞位移三阶段时程及其功率谱曲线Fig. 7 Time histories and frequency spectra of blade tip flapwise deflection at three stages
相比传统的“硬颤振”现象,“软颤振”没有明显的颤振发散临界点。考虑“软颤振”振动形态,选用风力机叶片3 s时距的叶根反力相对标准差斜率最大值指标δ,并定义其在高风速区间叶根反力颤振指标δ小于2%为临界点。因此,综合考虑叶尖位移均方差、叶根反力颤振指标δ对临界风速进行判定。图8给出了不同风速下颤振区间(桨距角93°~96°、284°~286°)与抖振工况(桨距角0°~360°)下的超长柔性风力机叶片δ-v(v为风洞风速)变化曲线。由图可见:所有桨距角下叶根反力颤振指标δ均随风速增大而逐渐变大;颤振工况(桨距角93°~96°、284°~286°)下的叶根反力颤振指标δ在颤振临界风速处存在突增的现象,且δ随风速变化呈非线性关系;对于抖振工况(桨距角0°~360°),叶根反力颤振指标δ随风速增加近似为一阶线性关系;当桨距角区间为93°~96°、284°~286°且风洞风速 分别低于5.4 m/s、6.0 m/s时,该区间桨距角下的叶根反力颤振指标δ均小于2%。
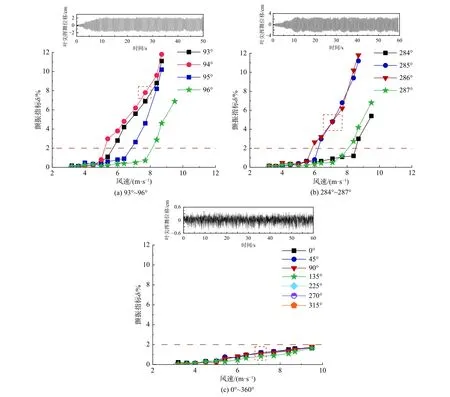
图8 不同桨距角区间下δ-v变化曲线Fig. 8 Relations between δ and v in three ranges of pitch angle
图9给出了由叶尖位移求得的不同桨距角区间内风力机叶片颤振临界风速。由图可知:颤振区间内的临界风速随桨距角的增大呈先减小后增大的趋势,在桨距角94°和286°时达到最小,对应的风洞临界风速为5.4 m/s和6.0 m/s(实际临界风速为45.2 m/s和50.2 m/s),颤振临界风速与拟合曲线吻合较好。因风力机叶片翼型的不对称,颤振区间呈190°反对称分布。
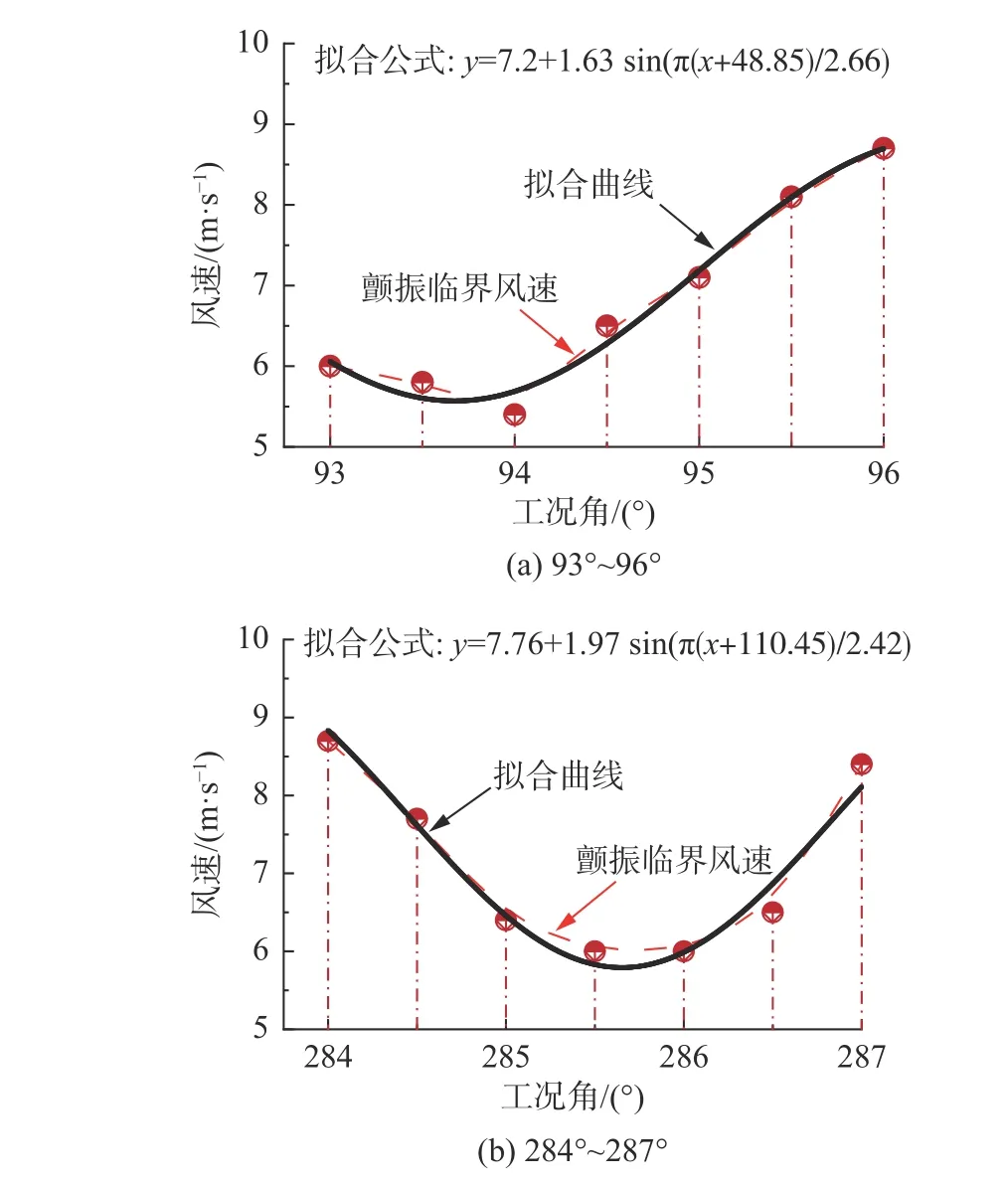
图9 不同桨距角区间风力机叶片颤振临界风速Fig. 9 Critical flutter wind speeds at different pitch angles
3.2 气动阻尼演化
叶片气弹失稳表现为某一阶或几阶气动阻尼提供的能量大于结构阻尼所能吸收的能量,导致叶片发生自激振动。风剪切作用下风力机叶片呈简谐振动,基于能量损失法,将每个转动周期内气动阻尼力所做的功等效为一个振动周期消耗的能量,通过一个振动周期内流体与叶片的做功关系对颤振是否发生进行评估——若在一个振动周期内流体对叶片做正功,系统不稳定,颤振发生;在一个周期内流体对叶片做负功,则系统稳定,颤振不发生。
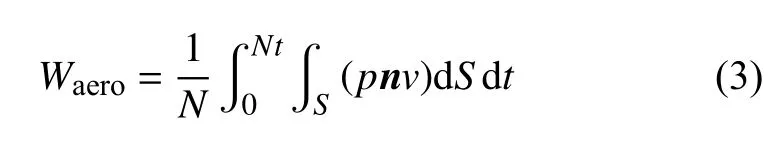
式中,Waero为一个振动周期内流体对叶片做的功,n为风力机叶片表面法向向量,v为风洞风速。颤振计算时常用无量纲量气动阻尼ξ评估系统是否稳定,气动阻尼与气动作功关系如式(4)所示:
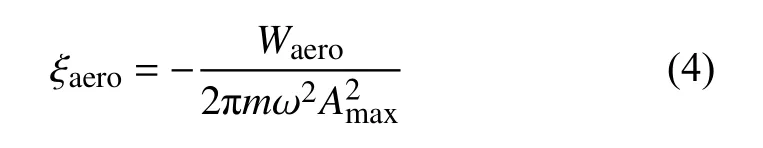
式中:ξ为风力机叶片气动阻尼,ω为振动角频率,Amax为叶尖最大位移,m为风力机叶片质量。
结构系统总阻尼比ξtot,由气动阻尼比ξaero和结构阻尼比ξstrut组成,即:
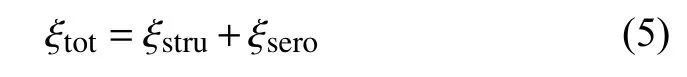
图10给出模型阻尼比随振幅的变化与模型阻尼比拟合曲线示意图。分析可知,试验模型阻尼比呈现随振幅增大而增大的特性,其中基于20个周期振动时程计算所得的阻尼比为0.23%,满足弹性模型设计要求。

图10 模型阻尼比随振幅的变化示意图Fig. 10 Variation of damping ratio with amplitude
图11和图12分别给出了不同桨距角下风力机叶片系统总阻尼比和气动阻尼比随风速变化规律。从图中可以看出,风力机叶片在89°~92°桨距角下未发生颤振,系统总阻尼比低风速下趋于0,且随风速增大系统总阻尼比整体呈增大趋势,而气动阻尼比变化规律与系统总阻尼比变化规律相同。颤振区间93°~96°、284°~286°内,叶片系统总阻尼比和气动阻尼比在低风速下趋于0,随后随风速的增大而增大,在达到峰值后又迅速减小并变为负值,逐渐抵消系统总阻尼比并驱动系统发散;当气动阻尼与结构阻尼比之和等于0时,系统趋于发散,此时(此处取桨距角94°和286°为例)风速分别为5.1 m/s和5.9 m/s,比试验颤振临界风速分别低了3.8%和6.3%,表明进入“软颤振”时,在系统总阻尼比趋于0的过程中,大振幅激励会逐渐衰减到稳定振幅,这说明颤振后气动阻尼作用明显。分析颤振区间气动阻尼变化规律可以发现,高风速下的气动负阻尼是驱动系统发散的主要原因,且风速越大气动负阻尼表现越明显,结构发生颤振越剧烈。

图11 不同桨距角下风力机叶片总阻尼变化规律Fig. 11 Variation of total damping of wind turbine blade with pitch angle
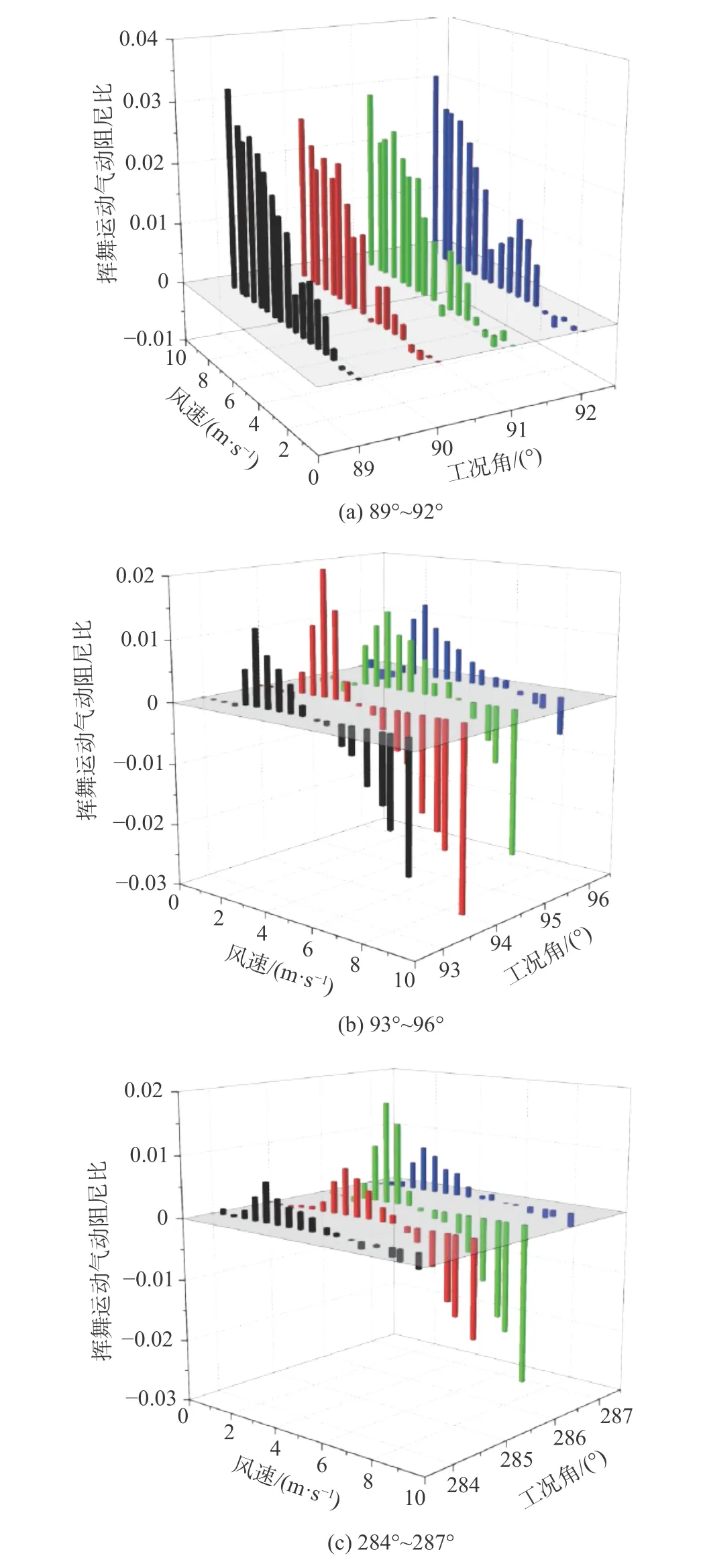
图12 不同桨距角下风力机叶片气动阻尼变化规律Fig. 12 Variation of aerodynamic damping of wind turbine blades with pitch angle
3.3 能量图谱
临界状态下风力机叶片的运动接近于单频的正弦运动,其挥舞及摆振运动位移和内力方程如下:
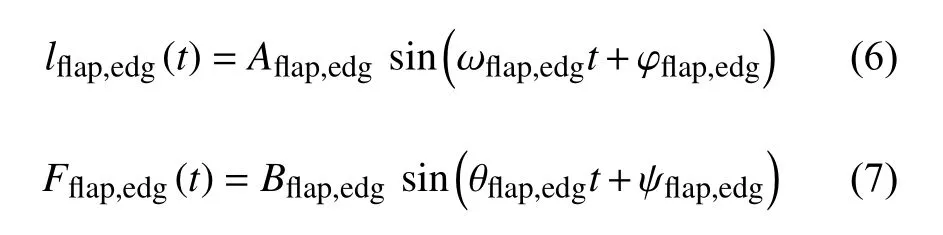
式中:Aflap,edg为风力机叶片挥舞和摆振运动的振幅,ωflap,edg为风力机叶片挥舞和摆振运动的频率,φflap,edg为风力机叶片挥舞和摆振运动初相位,Bflap,edg为风力机叶片挥舞和摆振内力的幅值,θflap,edg分别为风力机叶片挥舞和摆振内力的频率,ψflap,edg为风力机叶片挥舞和摆振内力初相位。
风力机叶片挥舞振动周期内力对挥舞运动做功的表达式为:
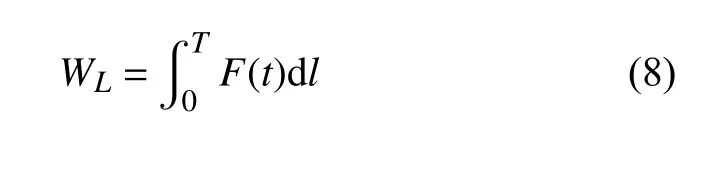
式中,T为风力机叶片挥舞、摆振振动周期,T= 2π/ω。
对大量不同桨距角和风速下的风洞试验数据进行分析(工况见图3),并基于式(8)得到风致振动函数做功与桨距角和风速关系的等值曲线图,即为表征风致振动做功效应的潜在能量演变图谱。图13给出了不同桨距角下风致振动潜在能量演变三维图谱,其能量演变二维图谱如图14所示。由图可知:非颤振工况下风致振动的能量分散,其值随风速的增大而增大,各桨距角在同一风速下能量无明显波动,当风速足够大时其能量积累增大,但明显低于颤振工况能量的积累;在颤振区间93°~96°、284°~286°桨距角下,存在能量积累突变界线,能量积累突变界线对应的风速随桨距角的增大呈先减小后增大的趋势,对比界线拟合公式,其变化趋势与颤振临界风速一致;超过能量积累突变界线后的能量积累现象显著,表明风致振动能量随时间呈现显著的非平稳特性。
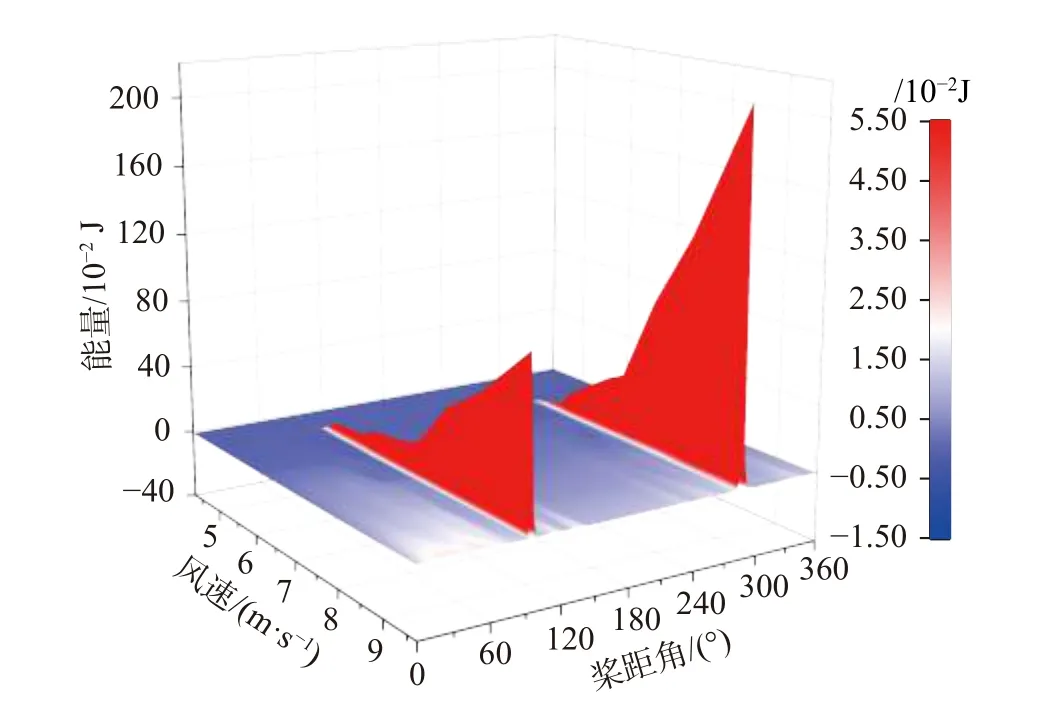
图13 不同桨距角下风致振动潜在能量演变三维图谱Fig. 13 Three-dimensional map of potential wind-induced vibration energy
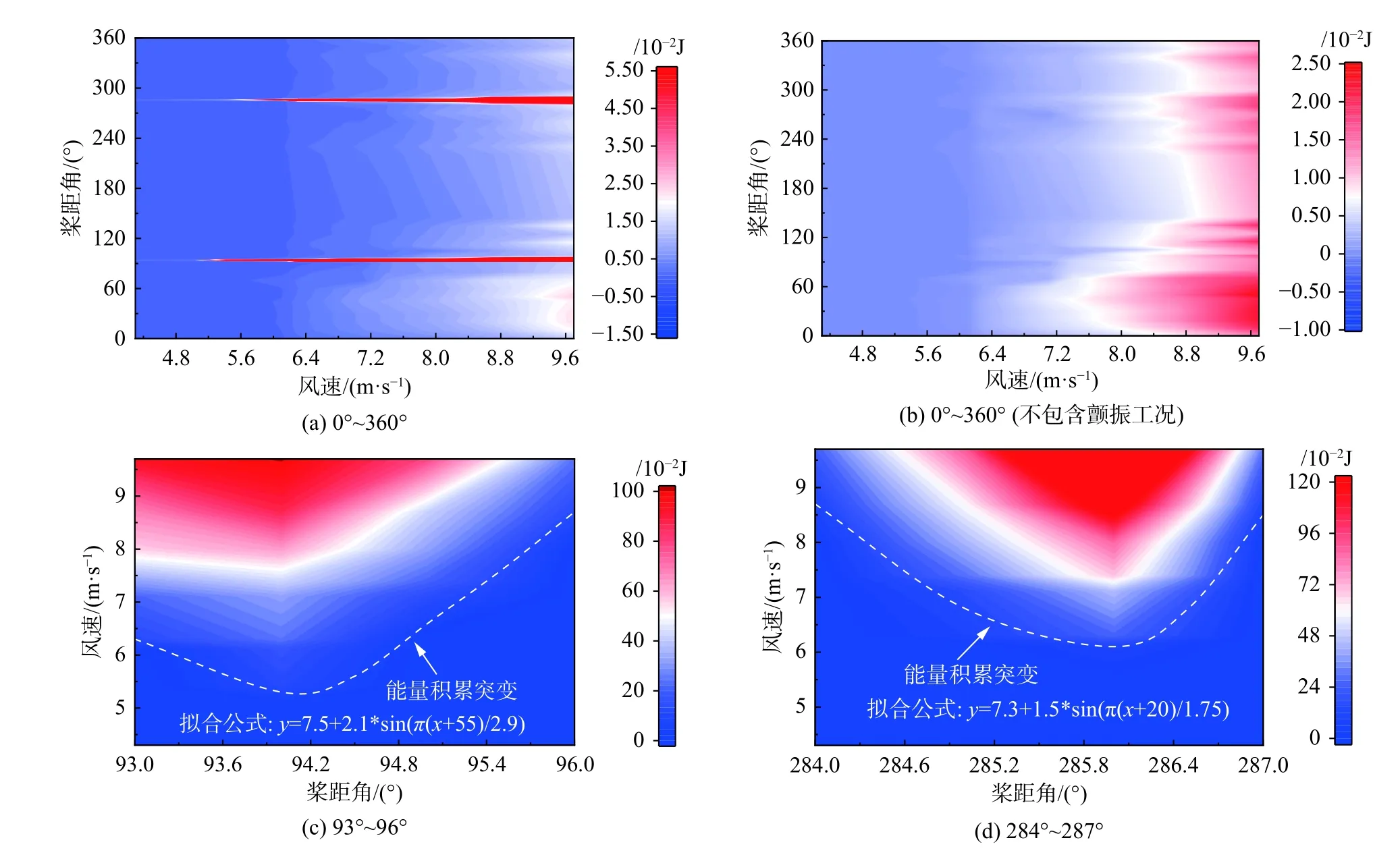
图14 不同桨距角下风致振动潜在能量演变图谱Fig. 14 Potential wind-induced vibration energy evolution at different pitch angle
图15 给出了能量随风速变化曲线。由图可知,颤振区间与非颤振区间的振动能量随风速的变化趋势相同,风速越大能量越分散,其均值分别随风速呈指数增长。相较于非颤振区间(能量最大值为0.025 J),颤振区间内的能量在达到颤振临界风速后积累显著,最大值可达1.5 J,是非颤振能量的60倍,表现出风力机叶片弹性模型风致振动能量随桨距角变化呈现显著的非平稳特性。
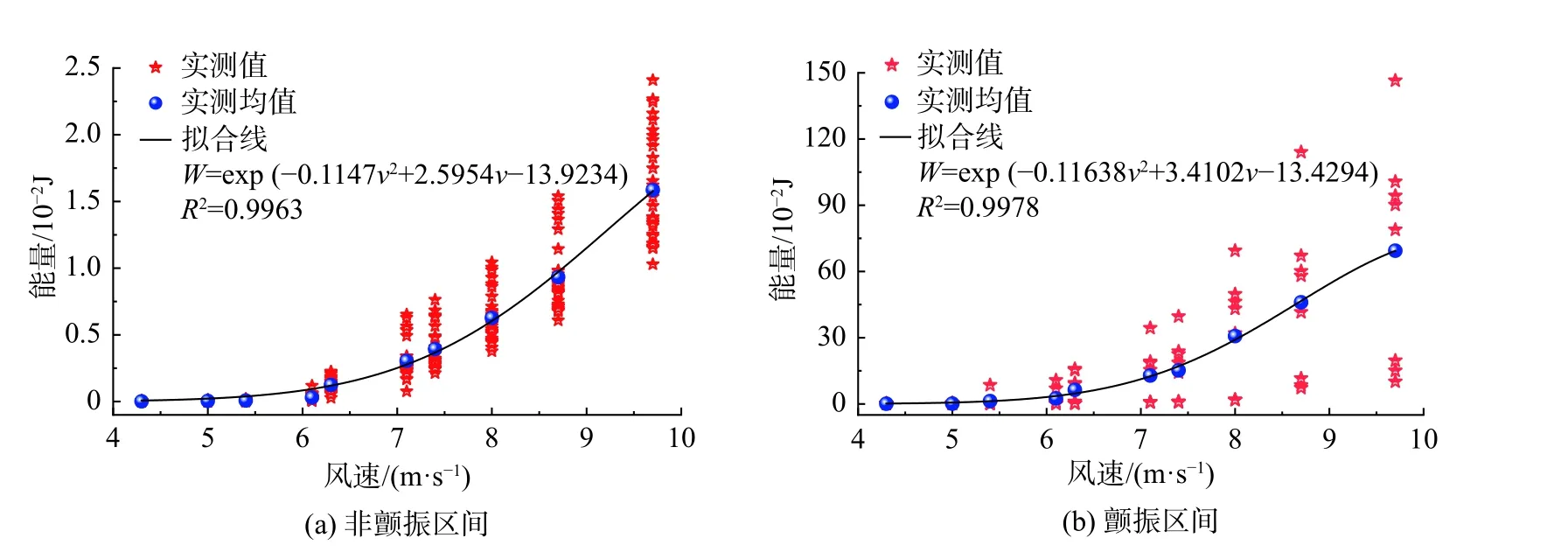
图15 能量随风速变化曲线及拟合公式示意图Fig. 15 Variation of energy with wind speed
4 结论
本文系统研究了15 MW风力机超长柔性叶片颤振后形态特性与作用机理,尤其在风力机叶片三维弹性模型设计、气动阻尼演化、能量图谱建立三个方面取得了原始创新。得到的具体结论如下:
1)提出一种基于主梁刚度等效原则的新型超长柔性风力机叶片气动-刚度-质量缩尺映射一体化三维弹性模型设计方法;采用高速摄像技术和高频六分量天平进行同步测振、测力风洞试验;验证了本文提出的弹性模型设计和试验方法能够精确有效地模拟风力机叶片动力性能与颤振行为。
2)风力机叶片在桨距角93°~96°和284°~286°区间属于风振敏感区间,在该区间叶片超过临界风速即可发生大幅锁频振动,而其余工况下呈现小幅随机振动状态;风力机叶片大幅锁频振动时程呈现三阶段非平稳振动,振幅随时间呈现先增大后平稳的趋势,表征为极限环振动。
3)在桨距角93°~96°、284°~286°下,气动阻尼比随风速达到峰值后又迅速减小,随后转负,逐渐抵消系统总阻尼比,并驱动系统发散;当气动阻尼与结构阻尼比之和等于0时系统趋于发散,此时桨距角94°、286°对应的风速分别为5.1 m/s、5.9 m/s,比试验风速分别低3.8%和6.3%,表明在颤振临界风速时系统总阻尼比趋于0,大振幅激励下会逐渐衰减到稳定振幅;进入颤振后状态,气动负阻尼是驱动系统发散的主要原因,且风速越大,气动负阻尼表现越明显,结构发生颤振越剧烈。
4)基于能量图谱分析方法,可分析颤振临界状态能量分散情况:非颤振工况下风致振动能量分散,能量积累明显低于颤振工况;颤振区间93°~96°、284°~286°下存在能量积累突变界线,能量积累突变界线对应的风速随桨距角的增大呈先减小后增大的趋势;超过能量积累突变界线的能量积累显著,表现出风致振动能量随时间和桨距角呈现显著的非平稳特性。

