几何最值问题的解题策略
⦿喀什大学数学与统计学院 陆文昊
1 引言
平面几何背景下的最值问题,其数学原理可追溯到“两点之间线段最短”“在直线外一点与直线上各点连接的所有线段中,垂线段最短”“三角形两边之和大于第三边”等几何学基本定理.苏教版八年级上册教科书初次介绍到“将军饮马”模型,即利用构造对称图形来解决两条线段和差及其延伸出的多边形周长最值问题.而我们通常认为的“胡不归”是以求“PA+kPB”形式的几何最值出现的,通过垂直构造直角三角形中的三角函数来处理系数k,从而完成思维上的过渡,将问题转化至求相连两条线段和的最值.本文将着重围绕这两大模型的例题展开剖析,对于更为复杂的最值模型,如“阿氏圆”“费马点”等,留给学有余力的学生继续探究,深化对解题原理与解题思路的理解[1].
2 例题解析
2.1 构造直角 转化系数

图1
例1在ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则的最小值等于.


图2
解析:如图2所示,过边CD上的动点P作PQ⊥AD,交AD的延长线于点Q.

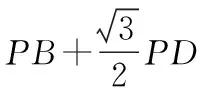
2.2 异端相接 回归本质
例2如图3,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为.

图3

图4
分析:初看本题,无法再从“胡不归”模型考虑.但无论从“将军饮马”还是“胡不归”的视角考虑,所求最短路径之和都由一个公共点相接,而此题的特殊之处在于两条线段是彼此独立.如此一来,我们不能将思路限制在两处的线段本身,而应通过必要的操作,将不常规的问题转化成熟悉的情形.
解析:充分利用中点D,设法找出与AE相接的BF的等效线段.如图4,过点C作CK⊥l于点K,过点A作AH⊥BC于点H.
在Rt△AHB中,∠ABC=60°,AB=2,
在Rt△AHC中,∠ACB=45°,
∵点D为BC中点,
∴BD=CD.
在△BFD与△CKD中,

∴△BFD≌△CKD(AAS).
∴BF=CK.
延长AE,过点C作CN⊥AE于点N,可得AE+BF=AE+CK=AE+EN=AN.

2.3 聚焦目标 化动为静
例3如图5,在边长为4的正方形ABCD中,将△ABD沿射线BD平移,得到△EGF,连接EC,GC.求EC+GC的最小值.
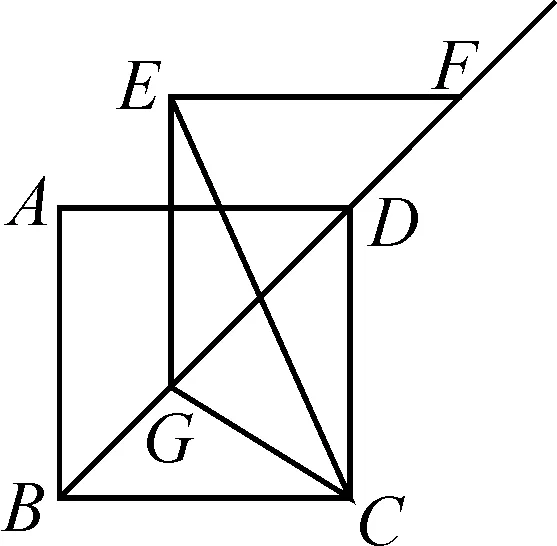
图5

图6
分析:本题中点E,G始终处在平移的动态中,我们仍需转化目标.尝试连结DE,AE,GC长等效到DE处,作点D关于直线AE的对称点T,这时可以得到“将军饮马”的雏形.再连结AT,ET,CT,易证B,A,T共线.
解析:通过上述辅助线的添加,得到图6.
∵四边形ABCD是正方形,
∴AB=BC=AD=4,
∠ABC= 90°,∠ABD=45°.
∵AE//BD,
∴∠EAD=∠ABD= 45°.
∵点D,T关于AE对称,
∴AD=AT=4,∠TAE=∠EAD= 45°.
∴∠TAD=90°.
∵∠BAD= 90°,
∴B,A,T三点共线.
又∵EG=CD,EG//CD,
∴四边形EGCD是平行四边形.
∴CG=DE.
∴EC+CG=EC+ED=EC+TE.
∵TE+EC≥TC,

趁热打铁,我们来看此类题型的一道拓展:


图7

图8
分析:观察点P的动态位置,BD,BC是天然存在的对称轴,作点P关于BD的对称点P1,关于BC的对应点P2,连接P1P2,分别交BD,BC于点M,N,此时得到△PNM周长最小;而四边形PMBN的面积问题根据轴对称的性质、等边三角形的性质、三角形三边关系以及外接圆的性质解答即可.


按分析中添辅助线的要求作出△PNM周长最小时的情形,如图8.
由对称的性质,可得
BP1=BP=BP2,
∠P1BM=∠PBM,∠P2BN=PBN,
MP1=MP,NP=NP2.
所以∠P1BP2= 2(∠PBM+ ∠PBN)=60°.
因此△P1BP2是等边三角形,有

过点B作BE⊥P1P2于点E,则

由轴对称的性质,可得△P1BM≌△PBM,△P2BN≌△PBN.当△BMN的面积最小时,四边形PMBN的面积最大.

图9
如图9,作△BMN的外接圆⊙O,连接OB,OM,ON,过点O作OF⊥MN于点F,∠MON=2∠MBN=60°,所以△MON是等边三角形.
设⊙O的半径为R,则
由OB+OF≥BE,得

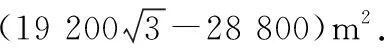
3 结论
通过对以上例题的探讨,笔者更希望给予学生几何最值问题的一种解题思路,在众多习题的特殊个性中洞悉数学本质的共性.几何最值问题属于平面几何的综合应用,除了将基本模型转化以外,主要还会结合三角形的性质、四边形的性质、解直角三角形、轴对称的性质、圆的性质等知识点,灵活应用先前建构起来的基础知识与基本技能完成解答[2].在“将军饮马”的动态过程中寻求不变与等效的量,在“胡不归”处理系数的选择上提高数感,均为提高解题能力之关键.

